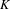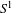Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Garkusha, Grigory
and
Panin, Ivan
2014.
The triangulated category of K-motives .
Journal of K-Theory,
Vol. 14,
Issue. 1,
p.
103.
Bachmann, Tom
2017.
The generalized slices of Hermitian
K
‐theory
.
Journal of Topology,
Vol. 10,
Issue. 4,
p.
1124.
Garkusha, Grigory
2018.
Comparing motives of smooth algebraic varieties.
Comptes Rendus. Mathématique,
Vol. 356,
Issue. 11-12,
p.
1100.
Garkusha, Grigory
2019.
Reconstructing rational stable motivic homotopy theory.
Compositio Mathematica,
Vol. 155,
Issue. 7,
p.
1424.
Garkusha, Grigory
and
Panin, Ivan
2020.
Framed motives of algebraic varieties (after V. Voevodsky).
Journal of the American Mathematical Society,
Vol. 34,
Issue. 1,
p.
261.
Garkusha, Grigory
and
Neshitov, Alexander
2023.
Fibrant resolutions for motivic Thom spectra.
Annals of K-Theory,
Vol. 8,
Issue. 3,
p.
421.
Garkusha, Grigory
2024.
Group schemes and motivic spectra.
Israel Journal of Mathematics,
Vol. 259,
Issue. 2,
p.
727.