Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Houdayer, Cyril
and
Ricard, Éric
2011.
Approximation properties and absence of Cartan subalgebra for free Araki–Woods factors.
Advances in Mathematics,
Vol. 228,
Issue. 2,
p.
764.
Ueda, Yoshimichi
2014.
Absence of Cartan subalgebras in continuous cores of free product von Neumann algebras.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 90,
Issue. 10,
Isono, Yusuke
2015.
Examples of factors which have no Cartan subalgebras.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 11,
p.
7917.
Houdayer, Cyril
and
Raum, Sven
2015.
Asymptotic structure of free Araki–Woods factors.
Mathematische Annalen,
Vol. 363,
Issue. 1-2,
p.
237.
Tomatsu, Reiji
and
Ueda, Yoshimichi
2016.
A characterization of the fullness of continuous cores of type III 1 free product factors.
Kyoto Journal of Mathematics,
Vol. 56,
Issue. 3,
Verraedt, Peter
2018.
Bernoulli Crossed Products Without Almost Periodic Weights.
International Mathematics Research Notices,
Vol. 2018,
Issue. 12,
p.
3684.

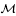 =
= 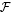 (
(