Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T03:45:33.259Z Has data issue: false hasContentIssue false
  • English
  • Français

ADJOINT FUNCTORS BETWEEN CATEGORIES OF HILBERT 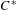$C^{\ast }$-MODULES

Part of: General theory of categories and functors Selfadjoint operator algebras

Published online by Cambridge University Press:  30 June 2016

Pierre Clare ,
Tyrone Crisp  and
Nigel Higson
Pierre Clare
Affiliation:
Department of Mathematics, Dartmouth College, HB 6188, Hanover, NH 03755, USA (clare@math.dartmouth.edu)
Tyrone Crisp
Affiliation:
Max-Planck-Institut für Mathematik, Vivatsgasse 7, 53111 Bonn, Germany (tyronecrisp@mpim-bonn.mpg.de)
Nigel Higson
Affiliation:
Department of Mathematics, Pennsylvania State University, University Park, PA 16802, USA (higson@math.psu.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 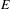$E$ be a (right) Hilbert module over a 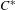$C^{\ast }$-algebra $A$. If 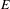$E$ is equipped with a left action of a second 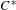$C^{\ast }$-algebra 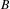$B$, then tensor product with 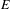$E$ gives rise to a functor from the category of Hilbert 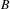$B$-modules to the category of Hilbert $A$-modules. The purpose of this paper is to study adjunctions between functors of this sort. We shall introduce a new kind of adjunction relation, called a local adjunction, that is weaker than the standard concept from category theory. We shall give several examples, the most important of which is the functor of parabolic induction in the tempered representation theory of real reductive groups. Each local adjunction gives rise to an ordinary adjunction of functors between categories of Hilbert space representations. In this way we shall show that the parabolic induction functor has a simultaneous left and right adjoint, namely the parabolic restriction functor constructed in Clare et al. [Parabolic induction and restriction via 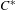$C^{\ast }$-algebras and Hilbert 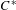$C^{\ast }$-modules, Compos. Math.FirstView (2016), 1–33, 2].

Keywords

Hilbert C∗ -modulesadjoint functorsparabolic induction

MSC classification

Primary: 46L08: $C^*$-modules 18A40: Adjoint functors (universal constructions, reflective subcategories, Kan extensions, etc.)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 2 , April 2018 , pp. 453 - 488
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beer, W., On Morita equivalence of nuclear C ∗ -algebras, J. Pure Appl. Algebra 26(3) (1982), 249–267.Google Scholar
Bernstein, J., Second adjointness for representations of reductive $p$ -adic groups. Draft: http://www.math.uchicago.edu/∼mitya/langlands.html, 1987.Google Scholar
Blecher, D. P., A new approach to Hilbert C ∗ -modules, Math. Ann. 307(2) (1997), 253–290.Google Scholar
Blecher, D. P. and Le Merdy, C., Operator Algebras and their Modules—An Operator Space Approach, London Mathematical Society Monographs. New Series, Volume 30 (The Clarendon Press, Oxford University Press, Oxford, 2004). Oxford Science Publications.Google Scholar
Clare, P., Hilbert modules associated to parabolically induced representations, J. Operator Theory 69(2) (2013), 483–509.CrossRefGoogle Scholar
Clare, P., Crisp, T. and Higson, N., Parabolic induction and restriction via C ∗ -algebras and Hilbert C ∗ -modules, Compos. Math. FirstView (2016), 1–33. 2.Google Scholar
Crisp, T. and Higson, N., Parabolic induction, categories of representations and operator spaces, to appear in Operator Algebras and their Applications: A Tribute to Richard V. Kadison, Contemporary Mathematics, Volume 671, (American Mathematical Society, Providence, RI, 2016).Google Scholar
Effros, E. G. and Ruan, Z.-J., Operator Spaces, London Mathematical Society Monographs. New Series, Volume 23 (The Clarendon Press, Oxford University Press, New York, 2000).Google Scholar
Frank, M. and Kirchberg, E., On conditional expectations of finite index, J. Operator Theory 40(1) (1998), 87–111.Google Scholar
Ghez, P., Lima, R. and Roberts, J. E., W ∗ -categories, Pacific J. Math. 120(1) (1985), 79–109.Google Scholar
Kajiwara, T., Pinzari, C. and Watatani, Y., Jones index theory for Hilbert C ∗ -bimodules and its equivalence with conjugation theory, J. Funct. Anal. 215(1) (2004), 1–49.Google Scholar
Lance, E. C., Hilbert C ∗ -modules, London Mathematical Society Lecture Note Series, Volume 210 (Cambridge University Press, Cambridge, 1995). A toolkit for operator algebraists.CrossRefGoogle Scholar
Mac Lane, S., Categories for the working mathematician, second edition, Graduate Texts in Mathematics, Volume 5 (Springer-Verlag, New York, 1998).Google Scholar
Miličić, D., Topological representation of the group C ∗ -algebra of SL(2, R), Glas. Mat. Ser. III 6(26) (1971), 231–246.Google Scholar
Morita, K., Adjoint pairs of functors and Frobenius extensions, Sci. Rep. Tokyo Kyoiku Daigaku Sect. A 9 (1965), 40–71. 1965.Google Scholar
Pavlov, A. A. and Troitskii, E. V., Quantization of branched coverings, Russ. J. Math. Phys. 18(3) (2011), 338–352.Google Scholar
Renard, D., Représentations des groupes réductifs p-adiques, Cours Spécialisés [Specialized Courses], Volume 17 (Société Mathématique de France, Paris, 2010).Google Scholar