Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T16:10:49.830Z Has data issue: false hasContentIssue false
  • English
  • Français

ALGEBRAIC FIBER SPACES AND CURVATURE OF HIGHER DIRECT IMAGES

Part of: Holomorphic functions of several complex variables

Published online by Cambridge University Press:  03 September 2020

Bo Berndtsson ,
Mihai Păun Open the ORCID record for Mihai Păun [Opens in a new window]  and
Xu Wang
Bo Berndtsson
Affiliation:
Department of Mathematical Sciences, Chalmers University of Technology and University of Gothenburg, SE-412 96Gothenburg, Sweden (bob@chalmers.se)
Mihai Păun
Affiliation:
Mathematisches Institut der Universität Bayreuth, Germany (mihai.paun@uni-bayreuth.de)
Xu Wang
Affiliation:
Department of Mathematical Sciences, Norwegian University of Science and Technology, NO-7491Trondheim, Norway (xu.wang@ntnu.no)
Get access Rights & Permissions [Opens in a new window]

Abstract

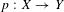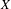Let $p:X\rightarrow Y$ be an algebraic fiber space, and let $L$ be a line bundle on $X$. In this article, we obtain a curvature formula for the higher direct images of 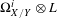$\unicode[STIX]{x1D6FA}_{X/Y}^{i}\otimes L$ restricted to a suitable Zariski open subset of 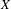$X$. Our results are particularly meaningful if $L$ is semi-negatively curved on 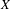$X$ and strictly negative or trivial on smooth fibers of 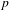$p$. Several applications are obtained, including a new proof of a result by Viehweg–Zuo in the context of a canonically polarized family of maximal variation and its version for Calabi–Yau families. The main feature of our approach is that the general curvature formulas we obtain allow us to bypass the use of ramified covers – and the complications that are induced by them.

Keywords

higher direct imags of relative canonical bundleHodge theoryposititivitycurvturesingular metrics

MSC classification

Secondary: 32A70: Functional analysis techniques
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 3 , May 2022 , pp. 973 - 1028
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aubin, T., Équations du type Monge-Ampère sur les varietés kählériennes compactes, Bull. Sci. Math. 102 (1978), 63–95.Google Scholar
Bănică, C. and Stănăşilă, O., Algebraic Methods in the Global Theory of Complex Spaces (John Wiley and Sons, New York, 1976).Google Scholar
Berndtsson, B., Curvature of vector bundles associated to holomorphic fibrations, Ann. Math. 169 (2009), 531–560.CrossRefGoogle Scholar
Berndtsson, B., Strict and nonstrict positivity of direct image bundles, Math. Z. 269 (2011), 1201–1218.CrossRefGoogle Scholar
Berndtsson, B. and Păun, M., Bergman kernel and the pseudo-effectivity of relative canonical bundles, Duke Math. J. 145 (2008), 341–378.CrossRefGoogle Scholar
Berndtsson, B. and Păun, M., Quantitative extensions of pluricanonical forms and closed positive currents, Nagoya Math. J. 205 (2012), 25–65.CrossRefGoogle Scholar
Brunebarbe, Y., Symmetric differentials and variations of Hodge structures, Crelle’s J. (2018), 133–163.CrossRefGoogle Scholar
Cao, J. and Păun, M., Kodaira dimension of algebraic fiber spaces over abelian varieties, Invent. Math. (2017) Preprint, 2015, arXiv:1504.01095.Google Scholar
Cattani, E., Kaplan, A. and Schmid, W., Degeneration of Hodge structures, Ann. of Math. (2) 123(3) (1986), 457–535.CrossRefGoogle Scholar
Choi, Y.-J., Positivity of direct images of fiberwise Ricci-flat metrics on Calabi–Yau fibrations, Preprint, 2015, arXiv:1508.00323.Google Scholar
Deligne, P., Équations Différentielles à Points Singuliers Réguliers, Lecture Notes in Mathematics, Volume 163, (Springer, Berlin, 1970).CrossRefGoogle Scholar
Demailly, J.-P., Algebraic criteria for Kobayashi hyperbolic projective varieties and jet differentials, in Algebraic Geometry–Santa Cruz 1995, Proceedings of Symposia in Pure Mathematics, Volume 62, Part 2, pp. 285–360 (American Mathematical Society, Providence, RI, 1997).CrossRefGoogle Scholar
Fujino, O. and Fujisawa, T., On semipositivity theorems, Preprint, 2017, arXiv:1701.02039, 2016, Math. Res. Lett. 26(5) (2019) 1359–1382.Google Scholar
Griffiths, P. (Ed.) Topics in Transcendental Algebraic Geometry, Annals of Mathematics Studies, (Princeton University Press, 1984).CrossRefGoogle Scholar
Griffiths, P. and Harris, J., Principles of Algebraic Geometry (John Wiley and Sons, 1978).Google Scholar
Griffiths, P. and Tu, L., Curvature properties of the Hodge bundles, in Topics in Transcendental Algebraic Geometry (Princeton, NJ, 1981/1982), Annals of Mathematics Studies, Volume 106, pp. 29–49 (Princeton University Press, Princeton, NJ, 1984).CrossRefGoogle Scholar
Kawamata, Y., Kodaira dimension of algebraic fiber spaces over curves, Invent. Math. 66(1) (1982), 57–71.CrossRefGoogle Scholar
Kebekus, S. and Kovács, S., Families of canonically polarized varieties over surfaces, Invent. Math. 172(3) (2008), 657–682.CrossRefGoogle Scholar
Kodaira, K. and Spencer, D. C., On deformations of complex analytic structures, III. Stability theorems for complex structures, Ann. Math. 71 (1960), 43–76.CrossRefGoogle Scholar
Kollár, J., Subadditivity of the Kodaira dimension: fibers of general type, in Algebraic Geometry, Sendai, 1985, Advanced Studies in Pure Mathematics, Volume 10, pp. 361–398 (North-Holland, Amsterdam, 1987).CrossRefGoogle Scholar
Kollár, J., Lectures on Resolution of Singularities, Annals of Mathematics Studies, Volume 166, (Princeton University Press, Princeton, NJ, 2007).Google Scholar
Mourougane, C. and Takayama, S., Hodge metrics and positivity of direct images, J. Reine Angew. Math. 606 (2007), 167–178.Google Scholar
Mourougane, C. and Takayama, S., Hodge metrics and the curvature of higher direct images, Ann. Sci. Éc. Norm. Supér. (4) 41 (2008), 905–924.CrossRefGoogle Scholar
Nakamaye, M., Stable base loci of linear series, Math. Ann. 318 (2000), 837–847.CrossRefGoogle Scholar
Nannicini, A., Weil–Petersson metric on the moduli space of Compact Polarized Kalar-Einstein Manifolds of Zero first Chern Class, Manuscripta Math. 54 (1986).CrossRefGoogle Scholar
Naumann, P., Curvature of higher direct images, Preprint, 2016, arXiv:1611.09117.Google Scholar
Păun, M., Relative adjoint transcendental classes and Albanese maps of compact Kähler manifolds with Nef Ricci curvature, Preprint, 2012, arXiv:1209.2915, Higher Dimensional Algebraic Geometry in Honour of Professor Yujiro Kawamata’s Sixtieth Birthday, Advanced Studies in Pure Mathematics, Volume 74, pp. 335–356 (Mathematical Society, Japan, Tokyo, 2017).Google Scholar
Păun, M. and Takayama, S., Positivity of relative twisted pluricanonical bundles and their direct images, Preprint, 2014, arXiv:1409.5504, J. Algebraic Geom. 27(2) (2018) 211–272.Google Scholar
Popa, M. and Schnell, C., Viehweg’s hyperbolicity conjecture for families with maximal variation, Preprint, 2015, arXiv:1511.00294, Invent. Math. 208(3) (2017) 677–713.Google Scholar
Popa, M. and Wu, L., Weak positivity for Hodge modules, Preprint, 2015,arXiv:1511.00290, Math. Res. Lett. 23(4) (2016) 1139–1155.Google Scholar
Royden, H., The extension of regular holomorphic maps, Amer. Math. Soc. 43 (1974), 306–310.CrossRefGoogle Scholar
Schumacher, G., Positivity of relative canonical bundles and applications, Invent. Math. 190 (2012), 1–56.CrossRefGoogle Scholar
Schumacher, G., Moduli of canonically polarized manifolds, higher order Kodaira–Spencer maps, and an analogy to Calabi–Yau manifolds, Preprint, 2017,arXiv:1702.07628.Google Scholar
Siu, Y. T., Curvature of the Weil–Petersson metric in the moduli space of compact Kähler–Einstein manifolds of negative first Chern class, in Contributions to Several Complex Variables, Aspects of Mathematics, Volume E9, pp. 261–298 (Vieweg, Braunschweig, 1986).Google Scholar
Siu, Y. T., Extension of twisted pluricanonical sections with plurisubharmonic weight and invariance of semipositively twisted plurigenera for manifolds not necessarily of general type, in Complex Geometry (Göttingen, 2000), pp. 223–277 (Springer, Berlin, 2002).CrossRefGoogle Scholar
Tian, G., Smoothness of the universal deformation space of compact Calabi–Yau manifolds and its Petersson-Weil metric, in Mathematical Aspects of String Theory (San Diego, Calif., 1986), Advanced Series in Mathematical Physics, Volume 1, pp. 629–646 (World Scientific Publishing, Singapore, 1987).CrossRefGoogle Scholar
To, W. K. and Yeung, S. K., Finsler Metrics and Kobayashi hyperbolicity of the moduli spaces of canonically polarized manifolds, Ann. Math. 181 (2015), 547–586.CrossRefGoogle Scholar
To, W. K. and Yeung, S. K., Augmented Weil–Petersson metrics on moduli spaces of polarized Ricci-flat Kähler manifolds and orbifolds, Asian J. Math. 22 (2018), 705–728.Google Scholar
Tosatti, V., Calabi–Yau manifolds and their degenerations, Ann. N.Y. Acad. Sci. 1260 (2012), 8–13.Google ScholarPubMed
Viehweg, E., Quasi-projective moduli for polarized manifolds, in Ergebnisse der Mathematik und ihrer Grenzgebiete, A Series of Modern Surveys in Mathematics.Google Scholar
Viehweg, E. and Zuo, K., Base spaces of non-isotrivial families of smooth minimal models, in Complex Geometry (Göttingen, 2000), pp. 279–328 (Springer, Berlin, 2002).Google Scholar
Viehweg, E. and Zuo, K., On the Brody hyperbolicity of moduli spaces for canonically polarized manifolds, Duke Math. J. 118 (2003), 103–150.CrossRefGoogle Scholar
Yeung, S. K., Sai-Kee Yeung Hyperbolicity problems on some family of polarized manifolds, in Talk at the Conference Komplexe Analysis (Oberwolfach, 2017).Google Scholar
Wang, C.-L., Curvature properties of the Calabi–Yau moduli, Doc. Math. 8 (2003), 577–590.Google Scholar
Wang, X., Curvature of higher direct image sheaves and its application on negative-curvature criterion for the Weil–Petersson metric, Preprint, 2016, arXiv:1607.03265 [math.CV].Google Scholar
Wang, X., Curvature restrictions on a manifold with a flat Higgs bundle, Preprint, 2016, arXiv:1608.00777.Google Scholar
Yau, S.-T., On the Ricci curvature of a compact Kähler manifold and the complex Monge-Ampére equation I, Comm. Pure Appl. Math. 31 (1978), 339–411.CrossRefGoogle Scholar
Yoshikawa, K.-I., to appear.Google Scholar
Zuo, K., On the negativity of kernels of Kodaira–Spencer maps on Hodge bundles and applications, Asian J. Math. 4(1) (2000), 279–301.CrossRefGoogle Scholar