Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T14:43:54.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Bergman metrics and geodesics in the space of Kähler metrics on principally polarized abelian varieties

Part of: Complex manifolds

Published online by Cambridge University Press:  21 June 2011

Renjie Feng
Renjie Feng
Affiliation:
Department of Mathematics, Northwestern University, 2033 Sheridan Road, Evanston, IL 60208-2730, USA (renjie@math.northwestern.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

It is well known in Kähler geometry that the infinite-dimensional symmetric space 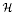of smooth Kähler metrics in a fixed Kähler class on a polarized Kähler manifold is well approximated by finite-dimensional submanifolds 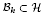of Bergman metrics of height k. Then it is natural to ask whether geodesics in 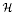can be approximated by Bergman geodesics in 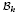. For any polarized Kähler manifold, the approximation is in the C0 topology. For some special varieties, one expects better convergence: Song and Zelditch proved the C2 convergence for the torus-invariant metrics over toric varieties. In this article, we show that some C∞ approximation exists as well as a complete asymptotic expansion for principally polarized abelian varieties.

Keywords

geodesicsBergman kernelKähler space of Kähler metrics

MSC classification

Secondary: 32Q15: Kähler manifolds
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 11 , Issue 1 , January 2012 , pp. 1 - 25
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Berline, N. and Vergne, M., Local Euler–Maclaurin formula for polytopes, Moscow Math. J. 7(3) (2007), 355–386.CrossRefGoogle Scholar
2.Berman, R., Berndtsson, B. and Sjöstrand, J., A direct approach to Bergman kernel asymptotics for positive line bundles, Ark. Mat. 46(2) (2008), 197–217.CrossRefGoogle Scholar
3.Berndtsson, B., Probability measures related to geodesics in the space of Kähler metrics, preprint (arxiv:0907.1806v2).Google Scholar
4.Chen, X. X., The space of Kähler metrics, J. Diff. Geom. 56 (2000), 189–234.Google Scholar
5.Donaldson, S. K., Symmetric spaces, Kähler geometry and Hamiltonian dynamics, in Northern California Symplectic Geometry Seminar, pp. 13–33 (American Mathematical Society, 1999).Google Scholar
6.Feng, R., Szasz analytic functions and noncompact Kähler toric manifolds, J. Geom. Analysis, in press (DOI: 10.1007/s12220-010-9198-0).CrossRefGoogle Scholar
7.Florentino, C. A., Mourão, J. M. and Nunes, J. P., Coherent state transforms and Abelian varieties, J. Funct. Analysis 192(2) (2002), 410–424.CrossRefGoogle Scholar
8.Griffiths, G. and Harris, J., Principles of algebraic geometry (Wiley-Interscience, 1978).Google Scholar
9.Guan, D., On modified Mabuchi functional and Mabuchi moduli space of Kähler metrics on toric bundles, Math. Res. Lett. 6 (1999), 547–555.(5–6)CrossRefGoogle Scholar
10.Guillemin, V. and Sternberg, S., Riemann sums over polytopes, Annales Inst. Fourier 57(7) (2007), 2183–2195.CrossRefGoogle Scholar
11.Hörmander, L., The analysis of linear partial differential operators, Grundlehren der mathematischen Wissenschaften, Volume 256 (Springer, 1983).Google Scholar
12.Kelmer, D., Arithmetic quantum unique ergodicity for symplectic linear maps of the multidimensional torus, Annals Math. 171(2) (2010), 815–879.CrossRefGoogle Scholar
13.Kurlberg, P. and Rudnick, Z., On quantum ergodicity for linear maps of the torus, Commun. Math. Phys. 222 (2001), 201–227.CrossRefGoogle Scholar
14.Mabuchi, T., Some symplectic geometry on compact Kähler manifolds, Osaka J. Math. 24 (1987), 227–252.Google Scholar
15.Mumford, D., Tata lectures on theta, I, Progress in Mathematics, Volume 28 (Birkhäuser, Boston, 1983).CrossRefGoogle Scholar
16.Phong, D. H. and Sturm, J., The Monge–Ampère operator and geodesics in the space of Kähler potentials, Invent. Math. 166(1) (2006), 125–149.CrossRefGoogle Scholar
17.Rubinstein, Y. A., Geometric quantization and dynamical constructions on the space of Kähler metrics, PhD thesis, MIT (2008).Google Scholar
18.Rubinstein, Y. A. and Zelditch, S., Bergman approximations of harmonic maps into the space of Kähler metrics on toric varieties, J. Symplectic Geom. 8(3) (2010), 239–265.CrossRefGoogle Scholar
19.Semmes, S., Complex Monge–Ampère and symplectic manifolds, Am. J. Math. 114 (1992), 495–550.CrossRefGoogle Scholar
20.Shiffman, B. and Zelditch, S., Almost holomorphic sections of ample line bundles over symplectic manifolds, J. Reine Angew. Math. 544 (2002), 181–222.Google Scholar
21.Sogge, C., Fourier integrals in classical analysis, Cambridge Tracts in Mathematics (1993).CrossRefGoogle Scholar
22.Song, J. and Zelditch, S., Convergence of Bergman geodesics on ℂℙ1, Annales Inst. Fourier 57(6) (2007), 2209–2237.CrossRefGoogle Scholar
23.Song, J. and Zelditch, S., Bergman metrics and geodesics in the space of Kähler metrics on toric varieties, Analysis PDEs 3(3) (2010), 295–358.CrossRefGoogle Scholar
24.Tian, G., On a set of polarized Kähler metrics on algebraic manifolds, J. Diff. Geom. 32 (1990), 99–130.Google Scholar
25.Zelditch, S., Szegö kernels and a theorem of Tian, Int. Math. Res. Not. 6 (1998), 317–331.CrossRefGoogle Scholar
26.Zelditch, S., Bernstein polynomials, Bergman kernels and toric Kähler varieties, J. Symplectic Geom. 7(2) (2009), 51–76.CrossRefGoogle Scholar