Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-11T04:12:26.741Z Has data issue: false hasContentIssue false
  • English
  • Français

BIG MAPPING CLASS GROUPS WITH HYPERBOLIC ACTIONS: CLASSIFICATION AND APPLICATIONS

Part of: Low-dimensional topology Special aspects of infinite or finite groups

Published online by Cambridge University Press:  31 May 2021

Camille Horbez Open the ORCID record for Camille Horbez [Opens in a new window] ,
Yulan Qing  and
Kasra Rafi
Camille Horbez
Affiliation:
Université Paris-Saclay, CNRS, Laboratoire de mathématiques d’Orsay, 91405, Orsay, France (camille.horbez@universite-paris-saclay.fr)
Yulan Qing
Affiliation:
Shanghai Center for Mathematical Sciences, Fudan University, Shanghai, China (qingyulan@fudan.edu.cn)
Kasra Rafi
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON, Canada (rafi@math.toronto.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We address the question of determining which mapping class groups of infinite-type surfaces admit nonelementary continuous actions on hyperbolic spaces.

More precisely, let 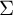$\Sigma $ be a connected, orientable surface of infinite type with tame endspace whose mapping class group is generated by a coarsely bounded subset. We prove that 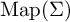${\mathrm {Map}}(\Sigma )$ admits a continuous nonelementary action on a hyperbolic space if and only if 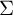$\Sigma $ contains a finite-type subsurface which intersects all its homeomorphic translates.

When 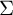$\Sigma $ contains such a nondisplaceable subsurface K of finite type, the hyperbolic space we build is constructed from the curve graphs of K and its homeomorphic translates via a construction of Bestvina, Bromberg and Fujiwara. Our construction has several applications: first, the second bounded cohomology of 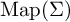${\mathrm {Map}}(\Sigma )$ contains an embedded 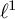$\ell ^1$ ; second, using work of Dahmani, Guirardel and Osin, we deduce that 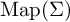${\mathrm {Map}} (\Sigma )$ contains nontrivial normal free subgroups (while it does not if 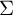$\Sigma $ has no nondisplaceable subsurface of finite type), has uncountably many quotients and is SQ-universal.

Keywords

mapping class groups of infinite-type surfacesgroup actions on hyperbolic spacesnormal subgroupsSQ-universalitybounded cohomologynondisplaceable subsurfaces

MSC classification

Primary: 20F65: Geometric group theory
Secondary: 20F67: Hyperbolic groups and nonpositively curved groups 57M60: Group actions in low dimensions
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 6 , November 2022 , pp. 2173 - 2204
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afton, S., Calegari, D., Chen, L. and Lyman, R., Nielsen realization for infinite-type surfaces, Proc. Amer. Math. Soc. 149(4) (2021), 1791–1799.CrossRefGoogle Scholar
Aougab, T., Patel, P. and Vlamis, N. G., ‘Isometry groups of infinite-genus hyperbolic surfaces’, Preprint, 2020, https://arxiv.org/pdf/2007.01982.pdf.Google Scholar
Aramayona, J., Fossas, A. and Parlier, H., Arc and curve graphs for infinite-type surfaces, Proc. Amer. Math. Soc. 145(11) (2017), 4995–5006.CrossRefGoogle Scholar
Aramayona, J., Ghaswala, T., Kent, A. E., McLeay, A., Tao, J. and Winarski, R. R., Big Torelli groups: Generation and commensuration, Groups Geom. Dyn. 13(4) (2019), 1373–1399.CrossRefGoogle Scholar
Aramayona, J., Patel, P., Vlamis, N. G., The first integral cohomology of pure mapping class groups, Int. Math. Res. Not. IMRN 2020(22) (2020), 8973–8996.CrossRefGoogle Scholar
Bavard, J., Hyperbolicité du graphe des rayons et quasi-morphismes sur un gros groupe modulaire, Geom. Topol. 20(1) (2016), 491–535.CrossRefGoogle Scholar
Bavard, J., Dowdall, S. and Rafi, K., Isomorphisms between big mapping class groups, Int. Math. Res. Not. IMRN 2020(10) (2020), 3084–3099.CrossRefGoogle Scholar
Bavard, J. and Genevois, A., Big mapping class groups are not acylindrically hyperbolic, Math. Slovaca 68(1) (2018), 71–76.CrossRefGoogle Scholar
Bavard, J. and Walker, A., ‘Two simultaneous actions of big mapping class groups’, Preprint, 2018, https://arxiv.org/pdf/1806.10272.pdf.Google Scholar
Bestvina, M., Bromberg, K. and Fujiwara, K., Constructing group actions on quasi-trees and applications to mapping class groups, Publ. Math. Inst. Hautes Études Sci. 122 (2015), 1–64.CrossRefGoogle Scholar
Bestvina, M., Bromberg, K. and Fujiwara, K., Stable commutator length on mapping class groups, Ann. Inst. Fourier (Grenoble) 66(3) (2016), 871–898.CrossRefGoogle Scholar
Bestvina, M. and Fujiwara, K., Bounded cohomology of subgroups of mapping class groups, Geom. Topol. 6 (2002), 69–89.CrossRefGoogle Scholar
Calegari, D., ‘Big mapping class groups and dynamics’, 2009, https://lamington.wordpress.com/2009/06/22/big-mapping-class-groups-and-dynamics/.Google Scholar
Calegari, D. and Chen, L., ‘Big mapping class groups and rigidity of simple circle’, Preprint, 2019, https://arxiv.org/pdf/1907.07903.pdf.Google Scholar
Caprace, P.-E., de Cornulier, Y., Monod, N. and Tessera, R., Amenable hyperbolic groups, J. Eur. Math. Soc. (JEMS) 17(11) (2015), 2903–2947.CrossRefGoogle Scholar
Clay, M., Mangahas, J. and Margalit, D., Right-angled Artin groups as normal subgroups of mapping class groups, Preprint, 2020, https://arxiv.org/pdf/2001.10587.pdf.Google Scholar
Coulon, R., Théroie de la petite simplification: Une approche géométrique, Astérisque 380 (2016), 1–33.Google Scholar
Dahmani, F., Guirardel, V. and Osin, D., Hyperbolically Embedded Subgroups and Rotating Families in Groups Acting on Hyperbolic Spaces, Memoirs of the American Mathematical Society, 245 (American Mathematical Society, Providence, RI, 2017).CrossRefGoogle Scholar
Domat, G., ‘Big pure mapping class groups are never perfect’, Preprint, 2020, https://arxiv.org/pdf/2007.14929.pdf. With an appendix by Dickmann, R. and Domat, G..Google Scholar
Durham, M. G., Fanoni, F. and Vlamis, N. G., Graphs of curves on infinite-type surfaces with mapping class group actions, Ann. Inst. Fourier (Grenoble) 68(6) (2019), 2581–2612.CrossRefGoogle Scholar
Fanoni, F., Ghaswala, T. and McLeay, A., ‘Homeomorphic subsurfaces and the omnipresent arcs’, Preprint, 2020, https://arxiv.org/pdf/2003.04750.pdf.CrossRefGoogle Scholar
Farb, B. and Margalit, D. A Primer on Mapping Class Groups, Princeton Mathematical Series, 49 (Princeton University Press, Princeton, NJ, 2012).Google Scholar
Gromov, M., Hyperbolic groups, in Essays in Group Theory, MSRI Publication, 8, pp. 75–265 (Springer-Verlag, New York, 1987).CrossRefGoogle Scholar
Guirardel, V., Geometric small cancellation, in Geometric Group Theory, IAS/Park City Mathematical Series, 21, pp. 55–90 (American Mathematical Society, Providence, RI, 2014).Google Scholar
Handel, M. and Mosher, L., ‘Second bounded cohomology and WWPD’, Preprint, 2019, https://arxiv.org/pdf/1901.01301.pdf.Google Scholar
Hernández Hernández, J., Morales, I. and Valdez, F., Isomorphisms between curve graphs of infinite-type surfaces are geometric, Rocky Mountain J. Math. 48(6) (2018), 1887–1904.CrossRefGoogle Scholar
Hernández Hernández, J., Morales, I. and Valdez, F., The Alexander method for infinite-type surfaces, Michigan Math. J. 68(4) (2019), 743–753.CrossRefGoogle Scholar
Kida, Y., Measure equivalence rigidity of the mapping class group, Ann. of Math. (2) 171(3) (2010), 1851–1901.CrossRefGoogle Scholar
Lyndon, R. C. and Schupp, P. E., Combinatorial Group Theory, Ergebnisse der Mathematik und ihrer Grenzgebiete, 89 (Springer-Verlag, Berlin, 1977).Google Scholar
Mann, K., ‘Automatic continuity for homeomorphism groups of noncompact manifolds’, Preprint, 2020, https://arxiv.org/pdf/2003.01173.pdf.Google Scholar
Mann, K. and Rafi, K., ‘Large scale geometry of big mapping class groups’, Preprint, 2019, https://arxiv.org/pdf/1912.10914.pdf.Google Scholar
Masur, H. A. and Minsky, Y. N., Geometry of the complex of curves I. Hyperbolicity, Invent. Math. 138(1) (1999), 103–149.CrossRefGoogle Scholar
Masur, H. A. and Minsky, Y. N., Geometry of the complex of curves II. Hierarchical structure, Geom. Funct. Anal. 10(4) (2000), 902–974.CrossRefGoogle Scholar
McLeay, A., ‘The mapping class group of the Cantor tree has only geometric normal subgroups’, Preprint, 2020, https://arxiv.org/pdf/2002.06970.pdf.CrossRefGoogle Scholar
Patel, P. and Vlamis, N., Algebraic and topological properties of big mapping class groups, Algebr. Geom. Topol. 18(7) (2018), 4109–4142.CrossRefGoogle Scholar
Rasmussen, A. J., ‘WWPD elements of big mapping class groups’, Preprint, 2019, https://arxiv.org/pdf/1909.06680.pdf.Google Scholar
Richards, I., On the classification of noncompact surfaces, Trans. Amer. Math. Soc. 106 (1963), 259–269.CrossRefGoogle Scholar
Rosendal, C., Coarse Geometry of Topological Groups, Book manuscript, http://homepages.math.uic.edu/~rosendal/PapersWebsite/Coarse-Geometry-Book23.pdf.Google Scholar