Hostname: page-component-7dd5485656-glrdx Total loading time: 0 Render date: 2025-10-31T20:16:00.586Z Has data issue: false hasContentIssue false
  • English
  • Français

A BOGOMOLOV UNOBSTRUCTEDNESS THEOREM FOR LOG-SYMPLECTIC MANIFOLDS IN GENERAL POSITION

Part of: Surfaces and higher-dimensional varieties Symplectic geometry, contact geometry Compact analytic spaces Deformations of analytic structures

Published online by Cambridge University Press:  09 November 2018

Ziv Ran
Ziv Ran*
Affiliation:
UC Math Department, Big Springs Road Surge Facility, Riverside CA 92521 US, USA (ziv.ran@ucr.edu). URL: http://math.ucr.edu/∼ziv/
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider compact Kählerian manifolds 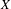$X$ of even dimension 4 or more, endowed with a log-symplectic holomorphic Poisson structure 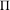$\unicode[STIX]{x1D6F1}$ which is sufficiently general, in a precise linear sense, with respect to its (normal-crossing) degeneracy divisor 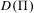$D(\unicode[STIX]{x1D6F1})$. We prove that 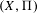$(X,\unicode[STIX]{x1D6F1})$ has unobstructed deformations, that the tangent space to its deformation space can be identified in terms of the mixed Hodge structure on 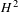$H^{2}$ of the open symplectic manifold 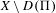$X\setminus D(\unicode[STIX]{x1D6F1})$, and in fact coincides with this 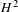$H^{2}$ provided the Hodge number 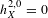$h_{X}^{2,0}=0$, and finally that the degeneracy locus 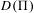$D(\unicode[STIX]{x1D6F1})$ deforms locally trivially under deformations of 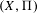$(X,\unicode[STIX]{x1D6F1})$.

Keywords

Poisson structurelog-symplectic manifolddeformation theorylog complexmixed Hodge theory

MSC classification

Primary: 32G07: Deformations of special (e.g. CR) structures 53D17: Poisson manifolds; Poisson groupoids and algebroids
Secondary: 14J40: $n$-folds ($n>4$) 32J27: Compact Kähler manifolds

Information

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 5 , September 2020 , pp. 1509 - 1519
Check for updates
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ciccoli, N., From Poisson to quantum geometry, Notes taken by P. Witkowski, available on http://toknotes.mimuw.edu.pl/sem4/files/Ciccoli_fpqg.pdf.Google Scholar
Deligne, P., Théorie de Hodge II, Publ. Math. Inst. Hautes Études Sci. (40) (1972), 5–57.Google Scholar
Dufour, J.-P. and Zung, N. T., Poisson Structures and Their Normal Forms, Prog. Math., Volume 242 (Birkhauser, Basel–Boston–Berlin, 2005).Google Scholar
Fiorenza, D. and Manetti, M., Formality of Koszul brackets and deformations of holomorphic Poisson manifolds, Homology, Homotopy Appl. 14 (2012), 63–75, arXiv:1109.4309v3.Google Scholar
Ginzburg, V. and Kaledin, D., Poisson deformations of symplectic quotient singularities, Adv. Math. 186 (2004), 1–57, arXiv:0212279v5.Google Scholar
Goto, R., Rozanski–Witten invariants of log-symplectic manifolds, in Integrable Systems, Topology, and Physics, Tokyo 2000, Contemporary Mathematics, Volume 309 (American Mathematical Society, Providence, RI, 2002).Google Scholar
Griffiths, P. and Schmid, W., Recent Developments in Hodge Theory, Discr. Subgr. Lie Groups & Appl. to Moduli, Proc. Int. Colloq. Bombay, pp. 31–127 (Oxford University Press, 1973).Google Scholar
Hitchin, N., Deformations of holomorphic Poisson manifolds, Preprint, 2011,arXiv:1105.4775v1.Google Scholar
Katzarkov, L., Kontsevich, M. and Pantev, T., Bogomolov–Tian–Todorov theorems for Landau–Ginzburg models, Preprint, 2014, arXiv:1409.5996.Google Scholar
Kontsevich, M., Generalized Tian–Todorov theorems, in Proceedings of Kinosaki Conference (Kyoto University, 2008). https://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/215060/1/2008-02.pdf.Google Scholar
Lima, R. and Pereira, J. V., A characterization of diagonal Poisson structures, Bull. Lond. Math. Soc. 46 (2014), 1203–1217.Google Scholar
Mǎrcut, I. and Torres, B. Osorno, Deformations of log symplectic structures, J. Lond. Math. Soc. (2) 90 (2014), 197–212.Google Scholar
Namikawa, Y., Flops and Poisson Deformations of Symplectic Varieties, Publications of the Research Institute for Mathematical Sciences, Volume 44, pp. 259–314 (Kyoto University, Kyoto, Japan, 2008).Google Scholar
Peters, C. A. M. and Steenbrink, J. H. M., Mixed Hodge Structures, Ergebnisse der Math. und ihrer Grenzgebiete 3. Folge (Springer, 2008).Google Scholar
Polishchuk, A., Algebraic geometry of Poisson brackets, J. Math. Sci. 84 (1997), 1413–1444.Google Scholar
Pym, B., Elliptic singularities on log symplectic manifolds and Feigin–Odeskii Poisson brackets, Preprint, 2015, arXiv:1507.05668.Google Scholar
Pym, B., Constructions and classifications of projective Poisson varieties, Preprint, 2017, arXiv:1701.08852v1.Google Scholar
Pym, B. and Schedler, T., Holonomic Poisson manifolds and deformations of elliptic algebras, Preprint, 2017, arXiv:1707.06035v1.Google Scholar
Ran, Z., Deformations of holomorphic pseudo-symplectic Poisson manifolds, Adv. Math. 304 (2017), 1156–1175, arXiv:1308.2442.Google Scholar