Article contents
Boundaries of instability zones for symplectic twist maps
Published online by Cambridge University Press: 08 February 2013
Abstract
Very few things are known about the curves that are at the boundary of the instability zones of symplectic twist maps. It is known that in general they have an irrational rotation number and that they cannot be KAM curves. We address the following questions. Can they be very smooth? Can they be non-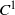 ${C}^{1} $?
${C}^{1} $?
Can they have a Diophantine or a Liouville rotation number? We give a partial answer for 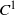 ${C}^{1} $ and
${C}^{1} $ and 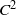 ${C}^{2} $ twist maps.
${C}^{2} $ twist maps.
In Theorem 1, we construct a 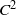 ${C}^{2} $ symplectic twist map
${C}^{2} $ symplectic twist map 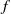 $f$ of the annulus that has an essential invariant curve
$f$ of the annulus that has an essential invariant curve 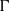 $\Gamma $ such that
$\Gamma $ such that
 $\bullet $
$\bullet $ 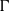 $\Gamma $ is not differentiable;
$\Gamma $ is not differentiable;
 $\bullet $ the dynamics of
$\bullet $ the dynamics of 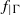 ${f}_{\vert \Gamma } $ is conjugated to the one of a Denjoy counter-example;
${f}_{\vert \Gamma } $ is conjugated to the one of a Denjoy counter-example;
 $\bullet $
$\bullet $ 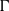 $\Gamma $ is at the boundary of an instability zone for
$\Gamma $ is at the boundary of an instability zone for 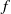 $f$.
$f$.
Using the Hayashi connecting lemma, we prove in Theroem 2 that any symplectic twist map restricted to an essential invariant curve can be embedded as the dynamics along a boundary of an instability zone for some 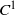 ${C}^{1} $ symplectic twist map.
${C}^{1} $ symplectic twist map.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 13 , Issue 1 , January 2014 , pp. 19 - 41
- Copyright
- ©Cambridge University Press 2013
References
- 4
- Cited by

