Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-27T13:42:37.772Z Has data issue: false hasContentIssue false
  • English
  • Français

Box splines and the equivariant index theorem

Part of: $K$-theory and operator algebras Topological $K$-theory Numerical approximation and computational geometry

Published online by Cambridge University Press:  01 June 2012

C. De Concini ,
C. Procesi  and
M. Vergne
C. De Concini
Affiliation:
Dipartimento di Matematica, Università di Roma La Sapienza, Piazzale Aldo Moro 5, 00185 Roma, Italia
C. Procesi
Affiliation:
Dipartimento di Matematica, Università di Roma La Sapienza, Piazzale Aldo Moro 5, 00185 Roma, Italia
M. Vergne
Affiliation:
Institut de Mathématiques de Jussieu, 175 rue du Chevaleret, 75013 Paris, France (vergne@math.jussieu.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we begin by recalling the inversion formula for the convolution with the box spline. The equivariant cohomology and the equivariant 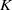$K$-theory with respect to a compact torus 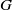$G$ of various spaces associated to a linear action of 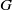$G$ in a vector space 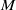$M$ can both be described using some vector spaces of distributions, on the dual of the group 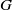$G$ or on the dual of its Lie algebra 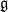$\mathfrak{g}$. The morphism from 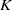$K$-theory to cohomology is analyzed, and multiplication by the Todd class is shown to correspond to the operator (deconvolution) inverting the semi-discrete convolution with a box spline. Finally, the multiplicities of the index of a 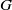$G$-transversally elliptic operator on 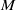$M$ are determined using the infinitesimal index of the symbol.

Keywords

splinesbox splinesdeconvolutionindex theoryequivariant K-theoryequivariant cohomologyRiemann–Rochelliptic operators

MSC classification

Secondary: 65D07: Splines 19L10: Riemann-Roch theorems, Chern characters 19L47: Equivariant $K$-theory 19K56: Index theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 3 , July 2013 , pp. 503 - 544
Copyright
©Cambridge University Press 2012 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atiyah, M. F., Elliptic operators and compact groups, L.N.M., Volume 401 (Springer, 1974).CrossRefGoogle Scholar
Atiyah, M. F. and Segal, G. B., The index of elliptic operators II, Ann. of Math. 87 (1968), 531–545.Google Scholar
Atiyah, M. F. and Singer, I. M., The index of elliptic operators I, Ann. of Math. 87 (1968), 484–530.CrossRefGoogle Scholar
Atiyah, M. F. and Singer, I. M., The index of elliptic operators III, Ann. of Math. 87 (1968), 546–604.Google Scholar
Berline, N., Getzler, E. and Vergne, M., Heat kernels and Dirac operators, Grundlehren der Mathematischen Wissenschaften, Volume 298 (Springer-Verlag, Berlin, 1992), viii+369 pp.Google Scholar
Berline, N. and Vergne, M., The equivariant index and Kirillov’s character formula, Amer. J. Math. 107 (1985), 1159–1190.CrossRefGoogle Scholar
Berline, Nicole and Vergne, Michèle, The Chern character of a transversally elliptic symbol and the equivariant index, Invent. Math. 124 (1996), 11–49.Google Scholar
Berline, Nicole and Vergne, Michèle, L’indice équivariant des opérateurs transversalement elliptiques, Invent. Math. 124 (1996), 51–101.Google Scholar
Brion, M. and Vergne, M., Residue formulae, vector partition functions and lattice points in rational polytopes, J. Amer. Math. Soc. 10 (1997), 797–833.Google Scholar
Dahmen, W. and Micchelli, C., On the solution of certain systems of partial difference equations and linear dependence of translates of box splines, Trans. Amer. Math. Soc. 292 (1985), 305–320.Google Scholar
Dahmen, W. and Micchelli, C., The number of solutions to linear Diophantine equations and multivariate splines, Trans. Amer. Math. Soc. 308 (1988), 509–532.CrossRefGoogle Scholar
De Boor, C., Hollig, K and Riemenschneider, S., Box splines, Applied Mathematical Sciences, Volume 98 (Springer-Verlag, New York, 1993).Google Scholar
De Concini, C. and Procesi, C., Toric arrangements, Transform. Groups 10 (2005), 387–422.Google Scholar
De Concini, C. and Procesi, C., Topics in hyperplane arrangements, polytopes and box-splines. Universitext (Springer-Verlag, New York, 2010), XXII+381 pp.Google Scholar
De Concini, C., Procesi, C. and Vergne, M., Vector partition functions and generalized Dahmen-Micchelli spaces, Transform. Groups 15 (4) (2010), 751–773.Google Scholar
De Concini, C., Procesi, C. and Vergne, M., Vector partition functions and index of transversally elliptic operators, Transform. Groups 15 (4) (2010), 775–811.Google Scholar
De Concini, C., Procesi, C. and Vergne, M., The infinitesimal index, JIMJ, in press (arXiv:1003.3525; 03/2010).Google Scholar
De Concini, C., Procesi, C. and Vergne, M., Infinitesimal index: cohomology computations, Transform. Groups 16 (2011), 717–735 (arXiv:math:1005.0128).Google Scholar
Khovanskiĭ, A. G. and Pukhlikov, A. V., The Riemann–Roch theorem for integrals and sums of quasipolynomials on virtual polytopes, Algebra i Analiz 4 (1992), 188–216.Google Scholar
Nelson, E., Operants: A functional calculus for non-commuting operators, in Functional analysis and related fields (Proc. conf. for M. Stone, Univ. Chicago, Chicago, Ill., 1968), pp. 172–187 (Springer, New York, 1970).Google Scholar
Paradan, P.-E. and Vergne, M., Quillen’s relative Chern character, in Algebraic analysis and around, Adv. Stud Pure Math., Volume 54 (Math. Soc., Japan, Tokyo, 2009) (arXiv:math:0702575).Google Scholar
Paradan, P.-E. and Vergne, M., Equivariant relative Thom forms and Chern characters (arXiv:math:0711.3898).Google Scholar
Paradan, P.-E. and Vergne, M., Equivariant Chern characters with generalized coefficients (arXiv:math/0801.2822).Google Scholar
Paradan, P.-E. and Vergne, M., The index of transversally elliptic operators, Astérisque 328 (2009), 297–338 (arXiv:0804.1225).Google Scholar
Vergne, M., A remark on the convolution with Box Splines, Ann. of Math. 174 (2011), 607–617 (arXiv:1003.1574).Google Scholar