Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-13T05:50:51.814Z Has data issue: false hasContentIssue false
  • English
  • Français

THE CRAMÉR–WOLD THEOREM ON QUADRATIC SURFACES AND HEISENBERG UNIQUENESS PAIRS

Part of: Nontrigonometric harmonic analysis

Published online by Cambridge University Press:  07 November 2017

Karlheinz Gröchenig  and
Philippe Jaming Open the ORCID record for Philippe Jaming [Opens in a new window]
Karlheinz Gröchenig
Affiliation:
Faculty of Mathematics, University of Vienna, Oskar-Morgenstern-Platz 1, A-1090 Vienna, Austria (karlheinz.groechenig@univie.ac.at)
Philippe Jaming
Affiliation:
Univ. Bordeaux, IMB, UMR 5251, F-33400 Talence, France CNRS, IMB, UMR 5251, F-33400 Talence, France (Philippe.Jaming@math.u-bordeaux.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

Two measurable sets 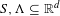$S,\unicode[STIX]{x1D6EC}\subseteq \mathbb{R}^{d}$ form a Heisenberg uniqueness pair, if every bounded measure $\unicode[STIX]{x1D707}$ with support in $S$ whose Fourier transform vanishes on 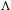$\unicode[STIX]{x1D6EC}$ must be zero. We show that a quadratic hypersurface and the union of two hyperplanes in general position form a Heisenberg uniqueness pair in 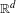$\mathbb{R}^{d}$. As a corollary we obtain a new, surprising version of the classical Cramér–Wold theorem: a bounded measure supported on a quadratic hypersurface is uniquely determined by its projections onto two generic hyperplanes (whereas an arbitrary measure requires the knowledge of a dense set of projections). We also give an application to the unique continuation of eigenfunctions of second-order PDEs with constant coefficients.

Keywords

uncertainty principleannihilating pairHeisenberg uniqueness pairCramér–Wold theorem

MSC classification

Primary: 42C20: Other transformations of harmonic type
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 1 , January 2020 , pp. 117 - 135
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Babot, D. B., Heisenberg uniqueness pairs in the plane. Three parallel lines, Proc. Amer. Math. Soc. 141 (2013), 3899–3904.Google Scholar
Bélisle, C., Massé, J.-C. and Ransford, Th., When is a probability measure determined by infinitely many projections, Ann. Probab. 25 (1997), 767–786.Google Scholar
Cramér, H. and Wold, H., Some theorems on distribution functions, J. Lond. Math. Soc. (2) 11 (1936), 290–294.Google Scholar
Dellacherie, C. and Meyer, P. A., Probabilities and Potential (North Holland, Amsterdam, 1978).Google Scholar
Fernández-Bertolin, A., Gröchenig, K. and Jaming, Ph., Heisenberg uniqueness pairs and unique continuation for harmonic functions and solutions of the Helmholtz equation. In preparation, technical report.Google Scholar
Gilbert, W. M., Projections of probability distributions, Acta Math. Acad. Sci. Hungar. 6 (1955), 195–198.Google Scholar
Hedenmalm, H. and Montes-Rodríguez, A., Heisenberg uniqueness pairs and the Klein–Gordon equation, Ann. of Math. (2) 173 (2011), 1507–1527.Google Scholar
Heppes, A., On the determination of probability distributions of more dimensions by their projections, Acta Math. Acad. Sci. Hungar. 7 (1956), 403–410.Google Scholar
Hohlweg, C., Labbé, J.-Ph. and Ripoll, V., Asymptotical behaviour of roots of infinite Coxeter groups, Canad. J. Math. 66 (2014), 323–353.Google Scholar
Jaming, Ph. and Kellay, K., A dynamical system approach to Heisenberg uniqueness pairs. J. Anal. Math., to appear, available on arXiv:arXiv:1312.6236.Google Scholar
Lev, N., Uniqueness theorems for Fourier transforms, Bull. Sci. Math. 135 (2011), 134–140.Google Scholar
Radin, C. and Sadum, L., On 2-generator subgroups of SO(3), Trans. Amer. Math. Soc. 351 (1999), 4469–4480.Google Scholar
Rényi, A., On projections of probability distributions, Acta Math. Acad. Sci. Hungar. 3 (1952), 131–142.Google Scholar
Sjölin, P., Heisenberg uniqueness pairs and a theorem of Beurling and Malliavin, Bull. Sci. Math. 135 (2011), 125–133.Google Scholar
Sjölin, P., Heisenberg uniqueness pairs for the parabola, J. Fourier Anal. Appl. 19 (2013), 410–416.Google Scholar
Giri, D. K. and Srivastava, R. K., Heisenberg uniqueness pairs for some algebraic curves in the plane, Adv. Math. 310 (2017), 993–1016.Google Scholar