Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T03:58:15.060Z Has data issue: false hasContentIssue false
  • English
  • Français

Diagrammes canoniques et représentations modulo p de GL2(F)

Part of: Lie groups

Published online by Cambridge University Press:  01 September 2010

Yongquan Hu
Yongquan Hu
Affiliation:
Département de Mathématiques, Bâtiment 425, Université de Paris-Sud, 91405 Orsay Cedex, France (yongquan.hu@math.u-psud.fr)
Get access Rights & Permissions [Opens in a new window]

Résumé

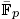Soit p un nombre premier et F un corps local non archimédien de caractéristique p. Dans cet article, à une représentation lisse irréductible de GL2(F) sur avec caractère central, nous associons un diagramme qui détermine la représentation de départ à isomorphisme près. Nous le déterminons également dans certains cas.

Keywords

représentation supersingulièrediagrammereprésentation de présentation finiesupersingular representationdiagramrepresentation of finite presentation

MSC classification

Secondary: 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 11 , Issue 1 , January 2012 , pp. 67 - 118
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Alperin, J. L., Local representation theory, Cambridge Studies in Advanced Mathematics, Volume 11 (Cambridge University Press, 1986).Google Scholar
2.Barthel, L. et Livné, R., Irreducible modular representations of GL2 of a local field, Duke Math. J. 75 (1994), 261–292.CrossRefGoogle Scholar
3.Barthel, L. et Livné, R., Modular representations of GL2 of a local field: unramified case, J. Number Theory 55 (1995), 1–27.CrossRefGoogle Scholar
4.Breuil, C., Sur quelques représentations modulaires et p-adiques de GL2(ℚp), I, Compositio Math. 138 (2003), 165–188.CrossRefGoogle Scholar
5.Breuil, C., Representations of Galois and of GL2 in characteristic p, Course at Columbia University (2007).Google Scholar
6.Breuil, C. et Paškūnas, V., Towards a modulo p Langlands correspondence for GL2, Mem. Am. Math. Soc., à paraître.Google Scholar
7.Buzzard, K., Diamond, F. et Jarvis, F., On Serre's conjecture for mod ℓ Galois representations over totally real fields, Duke Math. J., à paraître.Google Scholar
8.Colmez, P., Représentations de GL2(ℚp) et (φ, Γ)-modules, Astérisque 330 (2010), 281–509.Google Scholar
9.Emerton, M., Ordinary parts of admissible representations of p-adic reductive groups, I, Definition and first properties, Astérisque 331 (2010), 335–381.Google Scholar
10.Hu, Y., Sur quelques représentations supersingulières de GL2(ℚpf), J. Alg. 324 (2010), 1577–1615.CrossRefGoogle Scholar
11.Ollivier, R., Mod p representations of p-adic GL(2) and coefficient systems on the tree, prépublication (2009).Google Scholar
12.Paškūnas, V., Coefficient systems and supersingular representations of GL2(F), Mémoires de la Société Mathématique de France, Volume 99 (Société Mathématique de France, Paris, 2004).Google Scholar
13.Paškūnas, V., On the restriction of representations of GL2(F) to a Borel subgroup, Compositio Math. 143 (2007), 1533–1544.CrossRefGoogle Scholar
14.Paškūnas, V., Extensions for supersingular representations of GL2(ℚp), Astérisque 331 (2010), 317–353.Google Scholar
15.Schneider, P. et Vignéras, M.-F., A functor from smooth o-torsion representations to (φ, Γ)-modules, prépublication (2008).Google Scholar
16.Serre, J.-P., Corps locaux, 3ième édition (Hermann, Paris, 1968).Google Scholar
17.Vignéras, M.-F., Admissibilité des représentations p-adiques et lemme de Nakayama, prépublication (2007).Google Scholar
18.Vignéras, M.-F., A criterion for integral structures and coefficient systems on the tree of PGL (2, F), Pure Appl. Math. Q. 4(4) (2008), 1291–1316.CrossRefGoogle Scholar
19.Vignéras, M.-F., Le foncteur de Colmez pour GL2(F), prépublication (2009).Google Scholar