Article contents
EQUIVALENCE OF ELLIPTICITY AND THE FREDHOLM PROPERTY IN THE WEYL-HÖRMANDER CALCULUS
Published online by Cambridge University Press: 20 January 2021
Abstract
The main result is that the ellipticity and the Fredholm property of a 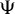 $\Psi $DO acting on Sobolev spaces in the Weyl-Hörmander calculus are equivalent when the Hörmander metric is geodesically temperate and its associated Planck function vanishes at infinity. The proof is essentially related to the following result that we prove for geodesically temperate Hörmander metrics: If
$\Psi $DO acting on Sobolev spaces in the Weyl-Hörmander calculus are equivalent when the Hörmander metric is geodesically temperate and its associated Planck function vanishes at infinity. The proof is essentially related to the following result that we prove for geodesically temperate Hörmander metrics: If 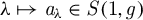 $\lambda \mapsto a_{\lambda }\in S(1,g)$ is a
$\lambda \mapsto a_{\lambda }\in S(1,g)$ is a 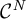 $\mathcal {C}^N$,
$\mathcal {C}^N$, 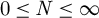 $0\leq N\leq \infty $, map such that each
$0\leq N\leq \infty $, map such that each 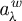 $a_{\lambda }^w$ is invertible on
$a_{\lambda }^w$ is invertible on 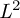 $L^2$, then the mapping
$L^2$, then the mapping 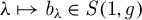 $\lambda \mapsto b_{\lambda }\in S(1,g)$, where
$\lambda \mapsto b_{\lambda }\in S(1,g)$, where 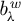 $b_{\lambda }^w$ is the inverse of
$b_{\lambda }^w$ is the inverse of 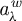 $a_{\lambda }^w$, is again of class
$a_{\lambda }^w$, is again of class 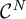 $\mathcal {C}^N$. Additionally, assuming also the strong uncertainty principle for the metric, we obtain a Fedosov-Hörmander formula for the index of an elliptic operator. At the very end, we give an example to illustrate our main result.
$\mathcal {C}^N$. Additionally, assuming also the strong uncertainty principle for the metric, we obtain a Fedosov-Hörmander formula for the index of an elliptic operator. At the very end, we give an example to illustrate our main result.
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 4 , July 2022 , pp. 1363 - 1389
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 2
- Cited by


