Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T20:18:14.288Z Has data issue: false hasContentIssue false
  • English
  • Français

EXPECTED TOPOLOGY OF RANDOM REAL ALGEBRAIC SUBMANIFOLDS

Part of: Geometric probability and stochastic geometry Complex manifolds

Published online by Cambridge University Press:  12 May 2014

Damien Gayet  and
Jean-Yves Welschinger
Damien Gayet
Affiliation:
Univ. Grenoble Alpes, IF, F-38000 Grenoble, France (damien.gayet@ujf-grenoble.fr) CNRS, IF, F-38000 Grenoble, France
Jean-Yves Welschinger
Affiliation:
Université de Lyon, CNRS UMR 5208, Université Lyon 1, Institut Camille Jordan, 43 blvd. du 11 novembre 1918, F-69622 Villeurbanne cedex, France (welschinger@math.univ-lyon1.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

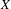Let $X$ be a smooth complex projective manifold of dimension $n$ equipped with an ample line bundle $L$ and a rank 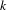$k$ holomorphic vector bundle 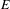$E$. We assume that 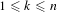$1\leqslant k\leqslant n$, that 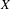$X$, 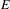$E$ and $L$ are defined over the reals and denote by 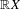$\mathbb{R}X$ the real locus of 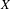$X$. Then, we estimate from above and below the expected Betti numbers of the vanishing loci in 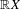$\mathbb{R}X$ of holomorphic real sections of 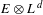$E\otimes L^{d}$, where 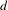$d$ is a large enough integer. Moreover, given any closed connected codimension 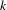$k$ submanifold 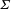${\it\Sigma}$ of 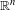$\mathbb{R}^{n}$ with trivial normal bundle, we prove that a real section of 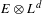$E\otimes L^{d}$ has a positive probability, independent of 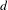$d$, of containing around 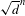$\sqrt{d}^{n}$ connected components diffeomorphic to 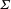${\it\Sigma}$ in its vanishing locus.

Keywords

real projective manifoldample line bundlerandom polynomialBetti numbers

MSC classification

Primary: 14P25: Topology of real algebraic varieties 32Q15: Kähler manifolds 60D05: Geometric probability and stochastic geometry
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 14 , Issue 4 , October 2015 , pp. 673 - 702
Copyright
© Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auffinger, A., Ben Arous, G. and Černý, J., Random matrices and complexity of spin glasses, Commun. Pure Appl. Math. 66(2) (2013), 165–201.Google Scholar
Bleher, P., Shiffman, B. and Zelditch, S., Universality and scaling of correlations between zeros on complex manifolds, Invent. Math. 142(2) (2000), 351–395.CrossRefGoogle Scholar
Bogomolny, E., Bohigas, O. and Leboeuf, P., Quantum chaotic dynamics and random polynomials, J. Statist. Phys. 85(5–6) (1996), 639–679.CrossRefGoogle Scholar
Bürgisser, P., Average Euler characteristic of random real algebraic varieties, C. R. Math. Acad. Sci. Paris 345(9) (2007), 507–512.CrossRefGoogle Scholar
Dedieu, J.-P. and Malajovich, G., On the number of minima of a random polynomial, J. Complexity 24(2) (2008), 89–108.Google Scholar
Demailly, J.-P., Estimations L 2 pour l’opérateur ∂̄ d’un fibré vectoriel holomorphe semi-positif au-dessus d’une variété kählérienne complète, Ann. Sci. Éc. Norm. Supér (4) 15(3) (1982), 457–511.Google Scholar
Donaldson, S. K., Symplectic submanifolds and almost-complex geometry, J. Differential Geom. 44(4) (1996), 666–705.CrossRefGoogle Scholar
Douglas, M. R., Shiffman, B. and Zelditch, S., Critical points and supersymmetric vacua I, Commun. Math. Phys. 252(1–3) (2004), 325–358.Google Scholar
Douglas, M. R., Shiffman, B. and Zelditch, S., Critical points and supersymmetric vacua II: Asymptotics and extremal metrics, J. Differential Geom. 72(3) (2006), 381–427.Google Scholar
Federer, H., Geometric measure theory, Die Grundlehren der mathematischen Wissenschaften, Band 153 (Springer-Verlag New York Inc., New York, 1969).Google Scholar
Fyodorov, Y. V., Complexity of random energy landscapes, glass transition, and absolute value of the spectral determinant of random matrices, Phys. Rev. Lett. 92(24) (2004), 240601, 4.CrossRefGoogle ScholarPubMed
Gayet, D., Hypersurfaces symplectiques réelles et pinceaux de Lefschetz réels, J. Symplectic Geom. 6(3) (2008), 247–266.CrossRefGoogle Scholar
Gayet, D. and Welschinger, J.-Y., Exponential rarefaction of real curves with many components, Publ. Math. Inst. Hautes Études Sci.(113) (2011), 69–96.CrossRefGoogle Scholar
Gayet, D. and Welschinger, J.-Y., Betti numbers of random real hypersurfaces and determinants of random symmetric matrices, J. Eur. Math. Soc. (2012), arXiv:1207.1579 (to appear).Google Scholar
Gayet, D. and Welschinger, J.-Y., What is the total Betti number of a random real hypersurface? J. Reine Angew. Math. (2012), published online, 10.1515/crelle-2012-0062.Google Scholar
Gayet, D. and Welschinger, J.-Y., Lower estimates for the expected Betti numbers of random real hypersurfaces, J. Lond. Math. Soc. (2013), arXiv:1303.3035 (to appear).Google Scholar
Hörmander, L., An Introduction to Complex Analysis in Several Variables (D Van Nostrand Co, Inc., Princeton, NJ; Toronto, Ont; London, 1966).Google Scholar
Kac, M., On the average number of real roots of a random algebraic equation, Bull. Amer. Math. Soc. 49 (1943), 314–320.Google Scholar
Kostlan, E., On the distribution of roots of random polynomials, in From Topology to Computation: Proceedings of the Smalefest (Berkeley, CA, 1990), pp. 419–431 (Springer, New York, 1993).Google Scholar
Lerario, A. and Lundberg, E., Statistics on Hilbert’s sixteenth problem, 2013 arXiv:212.3823.CrossRefGoogle Scholar
Ma, X. and Marinescu, G., Holomorphic Morse inequalities and Bergman kernels, (Progress in Mathematics, Volume 254), (Birkhäuser Verlag, Basel, 2007).Google Scholar
Macdonald, B., Density of complex critical points of a real random SO(m + 1) polynomial, J. Stat. Phys. 141(3) (2010), 517–531.CrossRefGoogle Scholar
Mehta, M. L., Random matrices. third edition, (Pure and Applied Mathematics (Amsterdam), volume 142), (Elsevier/Academic Press, Amsterdam, 2004).Google Scholar
Nash, J., Real algebraic manifolds, Ann. of Math. (2) 56 (1952), 405–421.Google Scholar
Nazarov, F. and Sodin, M., On the number of nodal domains of random spherical harmonics, Amer. J. Math. 131(5) (2009), 1337–1357.CrossRefGoogle Scholar
Nicolaescu, L. I., Critical sets of random smooth functions on compact manifolds, Asian J. Math. (2011), arXiv:1101.5990 (to appear).Google Scholar
Podkorytov, S. S., The mean value of the Euler characteristic of an algebraic hypersurface, Algebra i Analiz 11(5) (1999), 185–193.Google Scholar
Sarnak, P. and Wigman, I., Topologies of nodal sets of random band limited functions, 2013 arXiv:1312.7858.Google Scholar
Seifert, H., Algebraische Approximation von Mannigfaltigkeiten, Math. Z. 41(1) (1936), 1–17.CrossRefGoogle Scholar
Shiffman, B. and Zelditch, S., Distribution of zeros of random and quantum chaotic sections of positive line bundles, Comm. Math. Phys. 200(3) (1999), 661–683.Google Scholar
Shiffman, B. and Zelditch, S., Addendum: “Asymptotics of almost holomorphic sections of ample line bundles on symplectic manifolds” [J Reine Angew Math 544 (2002), 181–222; MR1887895 (2002m:58043)], Proc. Amer. Math. Soc. 131(1) (2003), 291–302.CrossRefGoogle Scholar
Shiffman, B. and Zelditch, S., Random polynomials of high degree and Levy concentration of measure, Asian J. Math. 7(4) (2003), 627–646.Google Scholar
Shiffman, B. and Zelditch, S., Number variance of random zeros on complex manifolds, Geom. Funct. Anal. 18(4) (2008), 1422–1475.CrossRefGoogle Scholar
Shub, M. and Smale, S., Complexity of Bezout’s theorem II Volumes and probabilities, in Comput. algebr. geom. (Nice, 1992), Progr. Math. Volume 109, pp. 267–285 (Birkhäuser, Boston, MA, 1993).CrossRefGoogle Scholar
Sodin, M., Lectures on random nodal portraits, Lecture Notes for a Mini-course Given at the St. Petersburg Summer School in Probability and Statistical Physics (June, 2012), 2012.Google Scholar
Sodin, M. and Tsirelson, B., Random complex zeros I Asymptotic normality, Israel J. Math. 144 (2004), 125–149.Google Scholar
Tian, G., On a set of polarized Kähler metrics on algebraic manifolds, J. Differential Geom. 32(1) (1990), 99–130.Google Scholar
Zelditch, S., Real and complex zeros of Riemannian random waves, in Spectral analysis in geometry and number theory, Contemp. Math., Volume 484, pp. 321–342 (Amer. Math. Soc., Providence, RI, 2009).CrossRefGoogle Scholar