Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T19:47:03.489Z Has data issue: false hasContentIssue false
  • English
  • Français

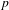FROM THE FUNCTION-SHEAF DICTIONARY TO QUASICHARACTERS OF $p$-ADIC TORI

Part of: Lie groups Algebraic groups (Co)homology theory

Published online by Cambridge University Press:  13 October 2015

Clifton Cunningham  and
David Roe
Clifton Cunningham
Affiliation:
Department of Mathematics and Statistics, University of Calgary, 2500 University Drive Northwest, Calgary, Alberta, CanadaT2N 1N4 (cunning@math.ucalgary.ca)
David Roe
Affiliation:
Department of Mathematics, University of British Columbia, 1984 Mathematics Road, Vancouver, British Columbia, CanadaV6T 1Z2 (roed.math@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the rigid monoidal category of character sheaves on a smooth commutative group scheme 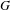$G$ over a finite field 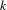$k$, and expand the scope of the function-sheaf dictionary from connected commutative algebraic groups to this setting. We find the group of isomorphism classes of character sheaves on 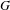$G$, and show that it is an extension of the group of characters of 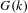$G(k)$ by a cohomology group determined by the component group scheme of 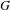$G$. We also classify all morphisms in the category character sheaves on 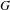$G$. As an application, we study character sheaves on Greenberg transforms of locally finite type Néron models of algebraic tori over local fields. This provides a geometrization of quasicharacters of 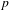$p$-adic tori.

Keywords

character sheavesp-adic toriNéron modelsGreenberg functorgeometrizationquasicharacter sheaves

MSC classification

Primary: 14F05: Sheaves, derived categories of sheaves and related constructions
Secondary: 14L15: Group schemes 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 1 , February 2018 , pp. 1 - 37
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aubert, A.-M. and Cunningham, C., An introduction to sheaves on adic spaces for p-adic group representation theory, in Functional Analysis, VII (Dubrovnik, 2001), Various Publications Series (Aarhus), Volume 46, pp. 11–51 (University Aarhus, Aarhus, 2002).Google Scholar
Beĭlinson, A. A., Bernstein, J. and Deligne, P., Faisceaux pervers, Astérisque 100 (1982), 5–171.Google Scholar
Bernstein, J., Stacks in representation theory: what is a representation of an algebraic group? in A Conference Dedicated to David Vogan on his 60th Birthday: Representations of Reductive Groups (MIT, 2014). May 22.Google Scholar
Bernstein, J. and Luntz, V., Equivariant Sheaves and Functors, Lecture Notes in Mathematics, Volume 1578 (Springer-Verlag, Berlin, 1994).Google Scholar
Bertapelle, A. and Gonzáles-Avilés, C. D., The Greenberg functor revisited, Preprint, 2014, arXiv:1311.0051 [math.NT].Google Scholar
Bitan, R. A., The discriminant of an algebraic torus, J. Number Theory 131(9) (2011), 1657–1671.CrossRefGoogle Scholar
Bosch, S., Lütkebohmert, W. and Reynaud, M., Néron Models (Springer-Verlag, Berlin, 1980).Google Scholar
Boyarchenko, M. and Drinfeld, V., A motivated introduction to character sheaves and the orbit method for unipotent groups in positive characteristic, Preprint, 2010, arXiv:0609769 [math.RT].Google Scholar
Brown, K. S., Cohomology of Groups, Graduate Texts in Mathematics, Volume 87 (Springer-Verlag, New York, 1982).Google Scholar
Cartan, H. and Eilenberg, S., Homological Algebra (Princeton University Press, Princeton, 1956).Google Scholar
Cassels, J. W. S. and Frohlich, A. (Eds.) Algebraic Number Theory, 2nd ed. (London Mathematical Society, London, 2010).Google Scholar
Chai, C.-L. and Yu, J.-K., Congruences of Néron models for tori and the Artin conductor, Ann. of Math. (2) 154(2) (2001), 347–382.CrossRefGoogle Scholar
Cunningham, C. and Kamgarpour, M., Geometrization of continuous characters of ℤ p × , Pacific J. Math. 261(1) (2013), 95–99.CrossRefGoogle Scholar
Deligne, P., Cohomologie étale, Lecture Notes in Mathematics, Volume 569 (Springer-Verlag, Berlin, 1977).Google Scholar
Deligne, P., La conjecture de Weil II, Publ. Math. Inst. Hautes Études Sci. 52 (1980), 137–252.Google Scholar
Deligne, P., Catégories tensorielles, Mosc. Math. J. 2(2) (2002), 227–248.CrossRefGoogle Scholar
Deligne, P. and Katz, N., Groupes de monodromie en géométrie algébrique II, Lecture Notes in Mathematics, Volume 340 (Springer-Verlag, Berlin, 1973).Google Scholar
Demazure, M. and Gabriel, P., Groupes algébriques (Masson & Cie, Paris, 1970).Google Scholar
Etingof, P., Gelaki, S., Nikshych, D. and Ostrik, V., Tensor categories, Lecture notes for MIT 18.769, 2009, Available at http://www-math.mit.edu/∼etingof/tenscat.pdf.Google Scholar
Geer, G. van der and Moonen, B., Abelian varieties, 2013, Available at http://staff.science.uva.nl/∼bmoonen/boek/BookAV.html.Google Scholar
Greenberg, M. J., Schemata over local rings I, Ann. of Math. (2) 73(2) (1961), 624–648.Google Scholar
Greenberg, M. J., Schemata over local rings II, Ann. of Math. (2) 78(2) (1963), 256–266.CrossRefGoogle Scholar
Grothendieck, A., Éléments de géométrie algébrique IV. Étude locale des schémas et des morphismes de schémas. II, Publ. Math. Inst. Hautes Études Sci. 24 (1965), 5–231.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique IV. Étude locale des schémas et des morphismes de schémas. III, Publ. Math. Inst. Hautes Études Sci. 28 (1966), 5–255.Google Scholar
Grothendieck, A., Séminaire de Géométrie Algébrique du Bois Marie 1965–66 SGA5: Cohomologie ℓ-adique et Fonctions L, Lecture Notes in Mathematics, Volume 589 (Springer-Verlag, Berlin, 1977).Google Scholar
Kamgarpour, M., Stacky abelianization of algebraic groups, Transform. Groups 14(4) (2009), 825–846.Google Scholar
Lang, S., Algebraic groups over finite fields, Amer. J. Math. 78 (1956), 555–563.Google Scholar
Laumon, G., Transformation de Fourier, constantes d’équations fonctionnelles et conjecture de Weil, Publ. Math. Inst. Hautes Études Sci. 65 (1987), 131–210.Google Scholar
Lusztig, G., Character sheaves I, Adv. Math. 56 (1985), 193–237.CrossRefGoogle Scholar
Lusztig, G., Character sheaves on disconnected groups I, Represent. Theory 7 (2003), 374–403.CrossRefGoogle Scholar
Sebag, J. and Nicaise, J., Motivic Serre invariants and Weil restriction, J. Algebra 319(4) (2008), 1585–1610.Google Scholar
Suzuki, T., Grothendieck’s pairing on Néron component groups: Galois descent from the semistable case, Preprint, 2015, arXiv:1410.3046 [math.NT].Google Scholar
Suzuki, T. and Yoshida, M., A refinement of the local class field theory of Serre and Hazewinkel, in Algebraic Number Theory and Related Topics, RIMS Kôkyûroku Bessatsu, Volume B32, pp. 163–191 (Research Institute for Mathematical Sciences (RIMS), Kyoto, 2012).Google Scholar
Vakil, R., Foundations of algebraic geometry, April 29, 2015, Available at http://math.stanford.edu/∼vakil/216blog/.Google Scholar
Vogan, D., The local Langlands conjecture, in Representation Theory of Groups and Algebras (ed. Adams, J. et al. ), Contemporary Mathematics, Volume 145 (American Mathematical Society, Providence, RI, 1993).Google Scholar
Weibel, C. A., An Introduction to Homological Algebra, Cambridge Studies in Advanced Mathematics, Volume 38 (Cambridge University Press, Cambridge, UK, 1994).Google Scholar
Yu, J.-K., On the local Langlands correspondence for tori, in Ottawa Lectures on Admissible Representations of Reductive p-adic Groups (ed. Cunningham, C. and Nevins, M.), Fields Institute Monographs, Volume 26, pp. 177–183 (American Mathematical Society, Providence RI, 2009).Google Scholar