Article contents
GEOMETRICAL AND MEASURE-THEORETIC STRUCTURES OF MAPS WITH A MOSTLY EXPANDING CENTER
Published online by Cambridge University Press: 12 July 2021
Abstract
In this article we study physical measures for 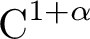 $\operatorname {C}^{1+\alpha }$ partially hyperbolic diffeomorphisms with a mostly expanding center. We show that every diffeomorphism with a mostly expanding center direction exhibits a geometrical-combinatorial structure, which we call skeleton, that determines the number, basins and supports of the physical measures. Furthermore, the skeleton allows us to describe how physical measures bifurcate as the diffeomorphism changes under
$\operatorname {C}^{1+\alpha }$ partially hyperbolic diffeomorphisms with a mostly expanding center. We show that every diffeomorphism with a mostly expanding center direction exhibits a geometrical-combinatorial structure, which we call skeleton, that determines the number, basins and supports of the physical measures. Furthermore, the skeleton allows us to describe how physical measures bifurcate as the diffeomorphism changes under 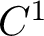 $C^1$ topology.
$C^1$ topology.
Moreover, for each diffeomorphism with a mostly expanding center, there exists a 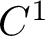 $C^1$ neighbourhood, such that diffeomorphism among a
$C^1$ neighbourhood, such that diffeomorphism among a 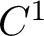 $C^1$ residual subset of this neighbourhood admits finitely many physical measures, whose basins have full volume.
$C^1$ residual subset of this neighbourhood admits finitely many physical measures, whose basins have full volume.
We also show that the physical measures for diffeomorphisms with a mostly expanding center satisfy exponential decay of correlation for any Hölder observes. In particular, we prove that every 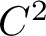 $C^2$, partially hyperbolic, accessible diffeomorphism with 1-dimensional center and nonvanishing center exponent has exponential decay of correlations for Hölder functions.
$C^2$, partially hyperbolic, accessible diffeomorphism with 1-dimensional center and nonvanishing center exponent has exponential decay of correlations for Hölder functions.
Keywords
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 2 , March 2023 , pp. 919 - 959
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 4
- Cited by


