Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T16:03:20.055Z Has data issue: false hasContentIssue false
  • English
  • Français

GLOBALLY REALIZABLE COMPONENTS OF LOCAL DEFORMATION RINGS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  03 September 2020

Frank Calegari ,
Matthew Emerton  and
Toby Gee Open the ORCID record for Toby Gee [Opens in a new window]
Frank Calegari
Affiliation:
Department of Mathematics, University of Chicago, 5734 S. University Ave., Chicago, IL60637, USA (fcale@math.uchicago.edu; emerton@math.uchicago.edu)
Matthew Emerton
Affiliation:
Department of Mathematics, University of Chicago, 5734 S. University Ave., Chicago, IL60637, USA (fcale@math.uchicago.edu; emerton@math.uchicago.edu)
Toby Gee
Affiliation:
Department of Mathematics, Imperial College London, LondonSW7 2AZ, UK (toby.gee@imperial.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

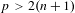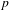Let $n$ be either $2$ or an odd integer greater than $1$, and fix a prime $p>2(n+1)$. Under standard ‘adequate image’ assumptions, we show that the set of components of $n$-dimensional $p$-adic potentially semistable local Galois deformation rings that are seen by potentially automorphic compatible systems of polarizable Galois representations over some CM field is independent of the particular global situation. We also (under the same assumption on $n$) improve on the main potential automorphy result of Barnet-Lamb et al. [Potential automorphy and change of weight, Ann. of Math. (2) 179(2) (2014), 501–609], replacing ‘potentially diagonalizable’ by ‘potentially globally realizable’.

Keywords

Galois representationsGalois deformationsautomorphic formscongruences

MSC classification

Primary: 11F33: Congruences for modular and $p$-adic modular forms 11F80: Galois representations
Secondary: 11F55: Other groups and their modular and automorphic forms (several variables)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 2 , March 2022 , pp. 533 - 602
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported in part by NSF Grants DMS-1404620 and DMS-1701703. The second author was supported in part by NSF Grants DMS-1303450, DMS-1601871, and DMS-1902307. The third author was supported in part by a Leverhulme Prize, EPSRC Grant EP/L025485/1, Marie Curie Career Integration Grant 303605, ERC Starting Grant 306326, and a Royal Society Wolfson Research Merit Award.

References

Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., Local-global compatibility for l = p, II, Ann. Sci. Éc. Norm. Supér. (4) 47(1) (2014), 165–179.CrossRefGoogle Scholar
Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., Potential automorphy and change of weight, Ann. of Math. (2) 179(2) (2014), 501–609.CrossRefGoogle Scholar
Bellaïche, J. and Chenevier, G., The sign of Galois representations attached to automorphic forms for unitary groups, Compos. Math. 147(5) (2011), 1337–1352.10.1112/S0010437X11005264CrossRefGoogle Scholar
Bellovin, R. and Gee, T., G-valued local deformation rings and global lifts, Algebra Number Theory 13(2) (2019), 333–378.10.2140/ant.2019.13.333CrossRefGoogle Scholar
Borel, A., Linear Algebraic Groups, 2nd ed., Graduate Texts in Mathematics, Volume 126 (Springer, New York, 1991).CrossRefGoogle Scholar
Bray, J. N., Holt, D. F. and Roney-Dougal, C. M., The Maximal Subgroups of the Low-dimensional Finite Classical Groups, London Mathematical Society Lecture Note Series, Volume 407 (Cambridge University Press, Cambridge, 2013). With a foreword by Martin Liebeck.CrossRefGoogle Scholar
Buzzard, K., Diamond, F. and Jarvis, F., On Serre’s conjecture for mod l Galois representations over totally real fields, Duke Math. J. 155(1) (2010), 105–161.CrossRefGoogle Scholar
Buzzard, K. and Gee, T., The Conjectural Connections Between Automorphic Representations and Galois Representations, Automorphic forms and Galois Representations, Volume 1, London Math. Soc. Lecture Note Series, Volume 414, pp. 135–187 (Cambridge University Press, Cambridge, 2014).Google Scholar
Calegari, F., Even Galois representations and the Fontaine–Mazur conjecture, Invent. Math. 185(1) (2011), 1–16.CrossRefGoogle Scholar
Calegari, F., Even Galois representations and the Fontaine–Mazur conjecture. II, J. Amer. Math. Soc. 25(2) (2012), 533–554.10.1090/S0894-0347-2011-00721-2CrossRefGoogle Scholar
Calegari, F. and Gee, T., Irreducibility of automorphic Galois representations of GL (n), n at most 5, Ann. Inst. Fourier (Grenoble) 63(5) (2013), 1881–1912.10.5802/aif.2817CrossRefGoogle Scholar
Caraiani, A., Local-global compatibility and the action of monodromy on nearby cycles, Duke Math. J. 161(12) (2012), 2311–2413.10.1215/00127094-1723706CrossRefGoogle Scholar
Caraiani, A., Monodromy and local-global compatibility for l = p , Algebra Number Theory 8(7) (2014), 1597–1646.CrossRefGoogle Scholar
Carayol, H., Sur les représentations galoisiennes modulo l attachées aux formes modulaires, Duke Math. J. 59(3) (1989), 785–801.CrossRefGoogle Scholar
Chenevier, G., On the infinite fern of Galois representations of unitary type, Ann. Sci. Éc. Norm. Supér. (4) 44(6) (2011), 963–1019.CrossRefGoogle Scholar
Clozel, L., Harris, M. and Taylor, R., Automorphy for some l-adic lifts of automorphic mod l Galois representations, Publ. Math. Inst. Hautes Études Sci. 108 (2008), 1–181. With Appendix A, summarizing unpublished work of Russ Mann, and Appendix B by Marie-France Vignéras. extra volume Coates, see https://www.math.uni-bielefeld.de/documenta/vol-coates/taylor.pdf.CrossRefGoogle Scholar
Conrad, B., Lifting global representations with local properties, Preprint, 2018.Google Scholar
Diamond, F. and Taylor, R., Lifting modular mod l representations, Duke Math. J. 74(2) (1994), 253–269.CrossRefGoogle Scholar
Dieulefait, L., Existence of families of Galois representations and new cases of the Fontaine–Mazur conjecture, J. Reine Angew. Math. 577 (2004), 147–151.Google Scholar
Emerton, M. and Gee, T., A geometric perspective on the Breuil–Mézard conjecture, J. Inst. Math. Jussieu 13(1) (2014), 183–223.CrossRefGoogle Scholar
Gee, T., A modularity lifting theorem for weight two Hilbert modular forms, Math. Res. Lett. 13(5–6) (2006), 805–811.CrossRefGoogle Scholar
Gee, T., Companion forms over totally real fields. II, Duke Math. J. 136(2) (2007), 275–284.CrossRefGoogle Scholar
Gee, T., Automorphic lifts of prescribed types, Math. Ann. 350(1) (2011), 107–144.Google Scholar
Gee, T. and Kisin, M., The Breuil–Mézard conjecture for potentially Barsotti–Tate representations, Forum Math. Pi 2 (2014), e1, 56.CrossRefGoogle Scholar
Harris, M., Potential automorphy of odd-dimensional symmetric powers of elliptic curves and applications, in Algebra, arithmetic, and geometry: in honor of Yu. I. Manin, Volume II, Progress in Mathematics, Volume 270, pp. 1–21 (Birkhäuser Boston Inc., Boston, MA, 2009).Google Scholar
Harris, M., Shepherd-Barron, N. and Taylor, R., A family of Calabi–Yau varieties and potential automorphy, Ann. of Math. (2) 171(2) (2010), 779–813.CrossRefGoogle Scholar
Khare, C. and Wintenberger, J.-P., On Serre’s conjecture for 2-dimensional mod p representations of Gal(ℚ/ℚ), Ann. of Math. (2) 169(1) (2009), 229–253.CrossRefGoogle Scholar
Kisin, M., The Fontaine–Mazur conjecture for GL2 , J. Amer. Math. Soc. 22(3) (2009), 641–690.10.1090/S0894-0347-09-00628-6CrossRefGoogle Scholar
Kisin, M., Moduli of finite flat group schemes, and modularity, Ann. of Math. (2) 170(3) (2009), 1085–1180.CrossRefGoogle Scholar
Larsen, M. and Pink, R., On l-independence of algebraic monodromy groups in compatible systems of representations, Invent. Math. 107(3) (1992), 603–636.CrossRefGoogle Scholar
Le Hung, B. V. and Li, C., Level raising mod 2 and arbitrary 2-Selmer ranks, Compos. Math. 152(8) (2016), 1576–1608.CrossRefGoogle Scholar
Liu, T. and Yu, J.-K., On automorphy of certain Galois representations of GO4 -type, J. Number Theory 161 (2016), 49–74. With an appendix by Liang Xiao.10.1016/j.jnt.2014.12.017CrossRefGoogle Scholar
Manoharmayum, J., A structure theorem for subgroups of GL n over complete local Noetherian rings with large residual image, Proc. Amer. Math. Soc. 143(7) (2015), 2743–2758.10.1090/S0002-9939-2015-12306-4CrossRefGoogle Scholar
Mitchell, H. H., The subgroups of the quaternary abelian linear group, Trans. Amer. Math. Soc. 15(4) (1914), 379–396.CrossRefGoogle Scholar
Moret-Bailly, L., Extensions de corps globaux à ramification et groupe de Galois donnés, C. R. Math. Acad. Sci. Paris Sér. I Math. 311(6) (1990), 273–276.Google Scholar
Patrikis, S., Variations on a theorem of Tate, Mem. Amer. Math. Soc. 258(1238) (2019), viii+156.Google Scholar
Patrikis, S. and Taylor, R., Automorphy and irreducibility of some l-adic representations, Compos. Math. 151(2) (2015), 207–229.CrossRefGoogle Scholar
Rajan, C. S., Unique decomposition of tensor products of irreducible representations of simple algebraic groups, Ann. of Math. (2) 160(2) (2004), 683–704.CrossRefGoogle Scholar
Ramakrishna, R., Deforming Galois representations and the conjectures of Serre and Fontaine–Mazur, Ann. of Math. (2) 156(1) (2002), 115–154.CrossRefGoogle Scholar
Serre, J.-P., Sur les représentations modulaires de degré 2 de Gal(Q /Q), Duke Math. J. 54(1) (1987), 179–230.CrossRefGoogle Scholar
Skinner, C. M. and Wiles, A. J., Base change and a problem of Serre, Duke Math. J. 107(1) (2001), 15–25.10.1215/S0012-7094-01-10712-6CrossRefGoogle Scholar
Taylor, R., Remarks on a conjecture of Fontaine and Mazur, J. Inst. Math. Jussieu 1(1) (2002), 125–143.CrossRefGoogle Scholar
Taylor, R., On the meromorphic continuation of degree two L-functions, Doc. Math. extra volume Coates (2006), 729–779 (electronic).Google Scholar
Taylor, R., Automorphy for some l-adic lifts of automorphic mod l Galois representations. II, Publ. Math. Inst. Hautes Études Sci. 108 (2008), 183–239.10.1007/s10240-008-0015-2CrossRefGoogle Scholar
Taylor, R., The image of complex conjugation in l-adic representations associated to automorphic forms, Algebra Number Theory 6(3) (2012), 405–435.CrossRefGoogle Scholar
Taylor, R. and Yoshida, T., Compatibility of local and global Langlands correspondences, J. Amer. Math. Soc. 20(2) (2007), 467–493.CrossRefGoogle Scholar
Thorne, J., On the automorphy of l-adic Galois representations with small residual image, J. Inst. Math. Jussieu 11(4) (2012), 855–920. With an appendix by R. Guralnick, F. Herzig, R. Taylor and Thorne.CrossRefGoogle Scholar
Xia, Y., Irreducibility of automorphic Galois representations of low dimensions, Math. Ann. 374(3–4) 1953–1986.CrossRefGoogle Scholar