Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T14:26:39.929Z Has data issue: false hasContentIssue false
  • English
  • Français

HALF NIKULIN SURFACES AND MODULI OF PRYM CURVES

Part of: Surfaces and higher-dimensional varieties Families, fibrations Curves

Published online by Cambridge University Press:  29 November 2019

Andreas Leopold Knutsen Open the ORCID record for Andreas Leopold Knutsen [Opens in a new window] ,
Margherita Lelli-Chiesa  and
Alessandro Verra
Andreas Leopold Knutsen
Affiliation:
Department of Mathematics, University of Bergen, Postboks 7800, 5020Bergen, Norway (andreas.knutsen@math.uib.no)
Margherita Lelli-Chiesa
Affiliation:
Dipartimento di Ingegneria e Scienze dell’Informazione e Matematica, Università degli Studi dell’Aquila, Via Vetoio, località Coppito, 67100L’Aquila, Italy (margherita.lellichiesa@univaq.it)
Alessandro Verra
Affiliation:
Dipartimento di Matematica, Università Roma Tre, Largo San Leonardo Murialdo, 00146Roma, Italy (verra@mat.uniroma3.it)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 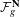${\mathcal{F}}_{g}^{\mathbf{N}}$ be the moduli space of polarized Nikulin surfaces 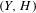$(Y,H)$ of genus $g$ and let 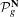${\mathcal{P}}_{g}^{\mathbf{N}}$ be the moduli of triples 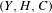$(Y,H,C)$, with 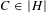$C\in |H|$ a smooth curve. We study the natural map $\unicode[STIX]{x1D712}_{g}:{\mathcal{P}}_{g}^{\mathbf{N}}\rightarrow {\mathcal{R}}_{g}$, where 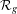${\mathcal{R}}_{g}$ is the moduli space of Prym curves of genus $g$. We prove that it is generically injective on every irreducible component, with a few exceptions in low genus. This gives a complete picture of the map 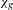$\unicode[STIX]{x1D712}_{g}$ and confirms some striking analogies between it and the Mukai map 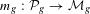$m_{g}:{\mathcal{P}}_{g}\rightarrow {\mathcal{M}}_{g}$ for moduli of triples 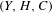$(Y,H,C)$, where 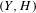$(Y,H)$ is any genus $g$ polarized $K3$ surface. The proof is by degeneration to boundary points of a partial compactification of 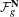${\mathcal{F}}_{g}^{\mathbf{N}}$. These represent the union of two surfaces with four even nodes and effective anticanonical class, which we call half Nikulin surfaces. The use of this degeneration is new with respect to previous techniques.

Keywords

Nikulin surfacesK3 surfacesdegenerationsPrym curves

MSC classification

Primary: 14J28: $K3$ surfaces and Enriques surfaces 14H10: Families, moduli (algebraic)
Secondary: 14D06: Fibrations, degenerations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 5 , September 2021 , pp. 1547 - 1584
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aprodu, M. and Farkas, G., Green’s Conjecture for general covers, in Compact Moduli Spaces and Vector Bundles, Contemporary Mathematics, Volume 564, pp. 211–226 (American Mathematical Society, Providence, RI, 2012).Google Scholar
Aprodu, M. and Farkas, G., The Green Conjecture for smooth curves lying on arbitrary K3 surfaces, Compos. Math. 147 (2011), 839–851.Google Scholar
Arbarello, E. and Bruno, A., Rank two vector bundles on polarized Halphen surfaces and the Gauss–Wahl map for du Val curves, J. Éc. Polytech. Math. 4 (2017), 257–285.Google Scholar
Arbarello, E., Bruno, A., Farkas, G. and Saccà, G., Explicit Brill–Noether–Petri general curves, Comment. Math. Helv. 91 (2016), 477–491.Google Scholar
Arbarello, E., Bruno, A. and Sernesi, E., Mukai’s program for curves on a K3 surface, Algebr. Geom. 1 (2014), 532–557.Google Scholar
Arbarello, E., Bruno, A. and Sernesi, E., On hyperplane sections of K3 surfaces, Algebr. Geom. 4 (2017), 562–596.Google Scholar
Ballico, E. and Homma, M., An inequality of Clifford indices for a finite covering of curves, Bol. Soc. Bras. Mat. 32 (2001), 145–147.Google Scholar
Chen, X., Rational curves on K3 surfaces, J. Algebraic Geom. 8 (1999), 245–278.Google Scholar
Ciliberto, C., Flamini, F., Galati, C. and Knutsen, A. L., Moduli of nodal curves on K3 surfaces, Adv. Math. 309 (2017), 624–654.Google Scholar
Ciliberto, C. and Knutsen, A. L., On k-gonal loci in Severi varieties on general K3 surfaces and rational curves on hyperkähler manifolds, J. Math. Pures Appl. (9) 101 (2014), 473–494.Google Scholar
Ciliberto, C., Lopez, A. F. and Miranda, R., Projective degenerations of K3 surfaces, Gaussian maps and Fano threefolds, Invent. Math. 114 (1993), 641–667.Google Scholar
Cossec, F. R. and Dolgachev, I. V., Enriques Surfaces. I, Progress in Mathematics, Volume 76 (Birkhäuser Boston, Inc., Boston, MA, 1989).Google Scholar
Dolgachev, I., Mirror symmetry for lattice polarized K3 surfaces, J. Math. Sci. 81 (1996), 2599–2630.Google Scholar
Farkas, G. and Kemeny, M., The Prym–Green conjecture for torsion line bundles of high order, Duke Math. J. 166 (2017), 1103–1124.Google Scholar
Farkas, G. and Popa, M., Effective divisors on M g, curves on K3 surfaces, and the slope conjecture, J. Algebraic Geom. 14 (2005), 241–267.Google Scholar
Farkas, G. and Verra, S., Moduli of theta characteristics via Nikulin surfaces, Math. Ann. 354 (2012), 465–496.Google Scholar
Feyzbakhsh, S., Mukai’s program (reconstructing a K3 surface from a curve) via wall-crossing, J. Reine Angew. Math., doi:10.1515/crelle-2019-0025.Google Scholar
Friedman, R., Global smoothings of varieties with normal crossings, Ann. of Math. (2) 118 (1983), 75–114.Google Scholar
Friedman, R., A new proof of the global Torelli theorem for K3 surfaces, Ann. of Math. (2) 120 (1984), 237–269.Google Scholar
Galati, C., Degenerating curves and surfaces: first results, Rend. Circ. Mat. Palermo (2) 58 (2009), 211–243.Google Scholar
Galati, C. and Knutsen, A. L., On the existence of curves with A k-singularities on K3 surfaces, Math. Res. Lett. 21 (2014), 1069–1109.Google Scholar
Garbagnati, A. and Sarti, A., Projective models of K3 surfaces with an even set, Adv. Geom. 8 (2008), 413–440.Google Scholar
Green, M. and Lazarsfeld, R., Special divisors on curves on a K3 surface, Invent. Math. 89 (1987), 357–370.Google Scholar
Griffiths, P. and Harris, J., On the Noether–Lefschetz theorem and some remarks on codimension-two cycles, Math. Ann. 271 (1985), 31–51.Google Scholar
Johnsen, T. and Knutsen, A. L., K3 Projective Models in Scrolls, Springer Lecture Notes in Mathematics, Volume 1842, p. 164 (Springer-Verlag, Berlin, 2004).Google Scholar
Knutsen, A. L., Exceptional curves on Del Pezzo surfaces, Math. Nachr. 256 (2003), 58–81.Google Scholar
Knutsen, A. L., On kth-order embeddings of K3 surfaces and Enriques surfaces, Manuscripta Math. 104 (2001), 211–237.Google Scholar
Knutsen, A. L., Lelli-Chiesa, M. and Verra, A., Moduli of non-standard Nikulin surfaces in low genus, arXiv:1802.01201, to appear in Ann. Sc. Norm. Super. Pisa Cl. Sci. (5), doi:10.2422/2036-2145.201802_018.Google Scholar
Kulikov, V., Degenerations of K3 surfaces and Enriques surfaces, Math. USSR Izv. 11 (1977), 957–989.Google Scholar
Lazarsfeld, R., Brill–Noether–Petri without degenerations, J. Differential Geom. 23 (1986), 299–307.Google Scholar
Lelli-Chiesa, M., Curves on surfaces with trivial canonical bundle, Boll. Unione Mat. Ital. 11 (2018), 93–105.Google Scholar
Mori, S. and Mukai, S., The uniruledness of the moduli space of curves of genus 11, in Algebraic Geometry, Proc. Tokyo/Kyoto, Lecture Notes in Mathematics, Volume 1016, pp. 334–353 (Springer, Berlin, 1983).Google Scholar
Mukai, S., Curves and K3 surfaces of genus eleven, in Moduli of Vector Bundles, Lecture Notes in Pure and Applied Mathematics, Volume 179, pp. 189–197 (Dekker, New York, 1996).Google Scholar
Mukai, S., Curves, K3 surfaces and Fano 3-folds of genus ⩽10, in Algebraic Geometry and Commutative Algebra, Vol. I, pp. 357–377 (Kinokuniya, Tokyo, 1988).Google Scholar
Mukai, S., Fano 3-folds, in Complex Projective Geometry, LMS Lecture Notes Series, Volume 179, pp. 255–261 (Cambridge University Press, Cambridge, 1992).Google Scholar
Nikulin, V. V., Kummer surfaces, Izv. Akad. Nauk SSSR 39 (1975), 278–293.Google Scholar
Persson, U. and Pinkham, H., Degenerations of surfaces with trivial canonical bundle, Ann. Math. 113 (1981), 45–66.Google Scholar
Saint-Donat, B., Projective models of K3 surfaces, Amer. J. Math. 96 (1974), 602–639.Google Scholar
Sernesi, E., Deformations of Algebraic Schemes, Grundlehren der mathematischen Wissenschaften, Volume 334 (Springer, Berlin Heidelberg, 2006).Google Scholar
van Geemen, B. and Sarti, A., Nikulin involutions on K3 surfaces, Math. Z. 255 (2007), 731–753.Google Scholar
Verra, A., Geometry of genus 8 Nikulin surfaces and rationality of their moduli, in K3 Surfaces and Their Moduli, Progress in Mathematics, Volume 315, pp. 345–364 (Birkhäuser, Springer, 2016).Google Scholar
Voisin, C., Green’s canonical syzygy conjecture for generic curves of odd genus, Compos. Math. 141 (2005), 1163–1190.Google Scholar
Voisin, C., Green’s generic syzygy conjecture for curves of even genus lying on a K3 surface, J. Eur. Math. Soc. (JEMS) 4 (2002), 363–404.Google Scholar
Wahl, J., On the cohomology of the square of an ideal sheaf, J. Algebraic Geom. 6 (1997), 481–511.Google Scholar
Wahl, J., The Jacobian algebra of a graded Gorenstein singularity, Duke Math. J. 55 (1987), 843–871.Google Scholar