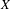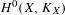Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Perry, Alexander
2022.
The integral Hodge conjecture for two-dimensional Calabi–Yau categories.
Compositio Mathematica,
Vol. 158,
Issue. 2,
p.
287.
Beckmann, Thorsten
and
de Gaay Fortman, Olivier
2023.
Integral Fourier transforms and the integral Hodge conjecture for one-cycles on abelian varieties.
Compositio Mathematica,
Vol. 159,
Issue. 6,
p.
1188.
Skauli, Bjørn
2023.
Curve classes on Calabi–Yau complete intersections in toric varieties.
Bulletin of the London Mathematical Society,
Vol. 55,
Issue. 2,
p.
811.
de Gaay Fortman, Olivier
2024.
On the integral Hodge conjecture for real abelian threefolds.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 0,
Issue. 0,
Lyu, Renjie
2025.
Cylinder maps of algebraic cycles on cubic hypersurfaces.
Bulletin of the London Mathematical Society,