Hostname: page-component-7f64f4797f-kjzhn Total loading time: 0 Render date: 2025-11-03T13:48:46.567Z Has data issue: false hasContentIssue false
  • English
  • Français

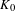ISOMORPHISMS UP TO BOUNDED TORSION BETWEEN RELATIVE $K_{0}$-GROUPS AND CHOW GROUPS WITH MODULUS

Part of: Cycles and subschemes Commutative algebra: Homological methods

Published online by Cambridge University Press:  18 March 2020

Ryomei Iwasa Open the ORCID record for Ryomei Iwasa [Opens in a new window]  and
Wataru Kai Open the ORCID record for Wataru Kai [Opens in a new window]
Ryomei Iwasa
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen Ø (ryomei@math.ku.dk)
Wataru Kai
Affiliation:
Mathematical Institute, Tohoku University, Aza-Aoba 6-3, Sendai 980-8578, Japan (kaiw@tohoku.ac.jp)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this note is to establish isomorphisms up to bounded torsion between relative 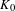$K_{0}$-groups and Chow groups with modulus as defined by Binda and Saito.

Keywords

algebraic K-theoryChow group with modulus

MSC classification

Primary: 13D15: Grothendieck groups, $K$-theory 14C25: Algebraic cycles 14C35: Applications of methods of algebraic $K$-theory

Information

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 6 , November 2021 , pp. 1947 - 1968
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020. Published by Cambridge University Press

References

Atiyah, M. and MacDonald, I., Introduction to Commutative Algebra (Addison-Wesley Publishing Co., Reading, MA–London-Don Mills, Ont., 1969).Google Scholar
Atiyah, M. and Tall, D., Group representations, 𝜆-rings and the J-homomorphism, Topology 8 (1969), 253–297.10.1016/0040-9383(69)90015-9CrossRefGoogle Scholar
Binda, F. and Krishna, A., Zero cycles with modulus and zero cycles on singular varieties, Compos. Math. 154 (2018), 120–187.10.1112/S0010437X17007503CrossRefGoogle Scholar
Binda, F. and Saito, S., Relative cycles with moduli and regulator maps, J. Inst. Math. Jussieu 18(6) (2019), 1233–1293.10.1017/S1474748017000391CrossRefGoogle Scholar
Bloch, S., Algebraic cycles and higher K-theory, Adv. Math. 61(3) (1986), 267–304.10.1016/0001-8708(86)90081-2CrossRefGoogle Scholar
Bloch, S., An elementary presentation for K-groups and motivic cohomology, in Motives (Seattle, WA, 1991), Proceedings of Symposia in Pure Mathematics, Volume 55, Part 1, pp. 239–244 (American Mathematical Society, Province, RI, 1994).Google Scholar
Dieudonné, J. and Grothendieck, A., Éléments de géométrie algébrique II, Publ. Math. Inst. Hautes Études Sci. 8 (1961), 5–222.Google Scholar
Fulton, W., Intersection Theory, Second edition, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, 2, (Springer, Berlin, 1998).10.1007/978-1-4612-1700-8CrossRefGoogle Scholar
Gillet, H. and Soulé, C., Intersection theory using Adams operations, Invent. Math. 90(2) (1987), 243–277.10.1007/BF01388705CrossRefGoogle Scholar
Iwasa, R., Relative K 0 and relative cycle class map, J. Pure Appl. Algebra 223 (2019), 48–71.10.1016/j.jpaa.2018.03.001CrossRefGoogle Scholar
Iwasa, R. and Kai, W., Chern classes with modulus, Nagoya Math. J. 236 (2019), 84–133.10.1017/nmj.2018.52CrossRefGoogle Scholar
Iwasa, R. and Krishna, A., Relative homotopy $K$ -theory and algebraic cycles with modulus, in preparation.Google Scholar
Krishna, A. and Park, J., Moving lemma for additive higher Chow groups, Algebra Number Theory 6(2) (2012), 293–326.10.2140/ant.2012.6.293CrossRefGoogle Scholar
Levine, M., Lambda-operations, K-theory and motivic cohomology, in Algebraic K-theory (Toronto, ON, 1996), Fields Inst. Commun., Volume 16, pp. 131–184 (American Mathematical Society, Province, RI, 1997).Google Scholar
Milnor, J. and Stasheff, J., Characteristic Classes, Annals of Mathematics Studies, Volume 76 (Princeton University Press; University of Tokyo Press, 1974).10.1515/9781400881826CrossRefGoogle Scholar
Miyazaki, H., Cube invariance of higher Chow groups with modulus, J. Algebraic Geom. 28 (2019), 339–390.10.1090/jag/726CrossRefGoogle Scholar
Soulé, C., Opérations en K-théorie algébrique, Canad. J. Math. 37(3) (1985), 488–550.10.4153/CJM-1985-029-xCrossRefGoogle Scholar
Thomason, R. W. and Trobaugh, T., Higher algebraic K-theory of schemes and of derived categories, in The Grothendieck Festschrift, Progress in Mathematics, Volume 88, pp. 247–435 (Brikhäuser Boston, Boston, 1990).10.1007/978-0-8176-4576-2_10CrossRefGoogle Scholar