Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T19:54:49.343Z Has data issue: false hasContentIssue false
  • English
  • Français

LA VARIANTE INFINITÉSIMALE DE LA FORMULE DES TRACES DE JACQUET-RALLIS POUR LES GROUPES LINÉAIRES

Published online by Cambridge University Press:  19 April 2016

Michał Zydor
Michał Zydor*
Affiliation:
Faculty of Mathematics and Computer Science, Weizmann Institute of Science, P.O. Box 26, Rehovot 76100, Israel (michalz@weizmann.ac.il)
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish an infinitesimal version of the Jacquet-Rallis trace formula for general linear groups. Our formula is obtained by integrating a kernel truncated à la Arthur multiplied by the absolute value of the determinant to the power 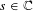$s\in \mathbb{C}$. It has a geometric side which is a sum of distributions 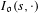$I_{\mathfrak{o}}(s,\cdot )$ indexed by the invariants of the adjoint action of 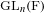$\text{GL}_{n}(\text{F})$ on 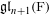$\mathfrak{gl}_{n+1}(\text{F})$ as well as a «spectral side» consisting of the Fourier transforms of the aforementioned distributions. We prove that the distributions 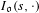$I_{\mathfrak{o}}(s,\cdot )$ are invariant and depend only on the choice of the Haar measure on 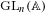$\text{GL}_{n}(\mathbb{A})$. For regular semi-simple classes $\mathfrak{o}$, 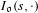$I_{\mathfrak{o}}(s,\cdot )$ is a relative orbital integral of Jacquet-Rallis. For classes $\mathfrak{o}$ called relatively regular semi-simple, we express 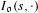$I_{\mathfrak{o}}(s,\cdot )$ in terms of relative orbital integrals regularised by means of zeta functions.

Nous établissons une variante infinitésimale de la formule des traces de Jacquet-Rallis pour les groupes linéaires. Notre formule s’obtient par intégration d’un noyau tronqué à la Arthur multiplié par la valeur absolue du déterminant à la puissance 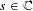$s\in \mathbb{C}$. Elle possède un côté géométrique qui est une somme de distributions 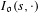$I_{\mathfrak{o}}(s,\cdot )$ indexées par les invariants de l’action de 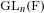$\text{GL}_{n}(\text{F})$ sur 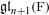$\mathfrak{gl}_{n+1}(\text{F})$ ainsi qu’un «côté spectral» formé des transformées de Fourier des distributions précédentes. On démontre que les distributions 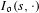$I_{\mathfrak{o}}(s,\cdot )$ sont invariantes et ne dépendent que du choix de la mesure de Haar sur 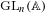$\text{GL}_{n}(\mathbb{A})$. Pour des classes $\mathfrak{o}$ semi-simples régulières, 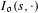$I_{\mathfrak{o}}(s,\cdot )$ est une intégrale orbitale relative de Jacquet-Rallis. Pour les classes $\mathfrak{o}$ dites relativement semi-simples régulières, on exprime 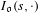$I_{\mathfrak{o}}(s,\cdot )$ en termes d’intégrales orbitales relatives régularisées à l’aide des fonctions zêta.

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 4 , September 2018 , pp. 735 - 783
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bibliographie

Arthur, J., A trace formula for reductive groups. I. Terms associated to classes in G (Q), Duke Math. J. 45(4) (1978), 911–952.Google Scholar
Arthur, J., The trace formula in invariant form, Ann. of Math. (2) 114(1) (1981), 1–74.Google Scholar
Chaudouard, P.-H., La formule des traces pour les algèbres de Lie, Math. Ann. 322(2) (2002), 347–382.Google Scholar
Gan, W. T., Gross, B. H. et Prasad, D., Symplectic local root numbers, central critical L values, and restriction problems in the representation theory of classical groups, Astérisque 346 (2012), 1–109. Sur les conjectures de Gross et Prasad. I.Google Scholar
Godement, R., Domaines fondamentaux des groupes arithmétiques. In Séminaire Bourbaki, 1962/63. Fasc. 3, No. 257, 1964.Google Scholar
Ichino, A. et Ikeda, T., On the periods of automorphic forms on special orthogonal groups and the Gross–Prasad conjecture, Geom. Funct. Anal. 19(5) (2010), 1378–1425.Google Scholar
Ichino, A. et Yamana, S., Periods of automorphic forms: the case of (GL n+1 × GL n , GL n ), Compos. Math. 151(4) (2015), 665–712.Google Scholar
Jacquet, H. et Rallis, S., On the Gross–Prasad conjecture for unitary groups, in On Certain L-Functions, Clay Math. Proc., vol. 13, pp. 205–265 (American Mathematical Society, 2011).Google Scholar
Knus, M.-A., Merkurjev, A., Rost, M. et Tignol, J.-P., The Book of Involutions, American Mathematical Society Colloquium Publications, vol. 44, (American Mathematical Society, Providence, RI, 1998). With a preface in French by J. Tits.Google Scholar
Labesse, J.-P. et Waldspurger, J.-L., La formule des traces tordue d’après le Friday Morning Seminar. Paris, 2009.Google Scholar
Mihatsch, A., On the arithmetic fundamental lemma through Lie algebras. Mathematische Zeitschrift. À paraître.Google Scholar
Neal Harris, R., The refined Gross–Prasad conjecture for unitary groups, Int. Math. Res. Not. IMRN 2014(2) (2014), 303–389.Google Scholar
Rapoport, M., Smithling, B. et Zhang, W., On the arithmetic transfer conjecture for exotic smooth formal moduli spaces. Prépublication arXiv:1503.06520v2, 2015.Google Scholar
Rapoport, M., Terstiege, U. et Zhang, W., On the arithmetic fundamental lemma in the minuscule case, Compos. Math. 149(10) (2013), 1631–1666.Google Scholar
Steve, R. et Gérard, S., Multiplicity one conjectures. Prépublication arXiv:0705.21268v1, 2008.Google Scholar
Zhang, W., On arithmetic fundamental lemmas, Invent. Math. 188(1) (2012), 197–252.Google Scholar
Zhang, W., Automorphic period and the central value of Rankin–Selberg L-function, J. Amer. Math. Soc. 27 (2014), 541–612.Google Scholar
Zhang, W., Fourier transform and the global Gan–Gross–Prasad conjecture for unitary groups, Ann. of Math. (2) 180(3) (2014), 971–1049.Google Scholar
Zydor, M., La variante infinitésimale de la formule des traces de Jacquet-Rallis pour les groupes unitaires. Canad. J. Math. À paraître.Google Scholar
Zydor, M., Les formules des traces relatives de Jacquet-Rallis grossières. Prépublication arXiv:1510.04301, 2015.Google Scholar