Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T09:18:24.452Z Has data issue: false hasContentIssue false
  • English
  • Français

LARGE FIELDS IN DIFFERENTIAL GALOIS THEORY

Part of: Differential and difference algebra Linear algebraic groups and related topics General field theory Field extensions Curves

Published online by Cambridge University Press:  27 January 2020

Annette Bachmayr Open the ORCID record for Annette Bachmayr [Opens in a new window] ,
David Harbater ,
Julia Hartmann  and
Florian Pop
Annette Bachmayr
Affiliation:
Institut für Mathematik, Johannes Gutenberg Universität Mainz, 55128Mainz, Germany (abachmay@uni-mainz.de)
David Harbater
Affiliation:
Department of Mathematics, University of Pennsylvania, Philadelphia, PA19104-6395, USA (harbater@math.upenn.edu; hartmann@math.upenn.edu; pop@math.upenn.edu)
Julia Hartmann
Affiliation:
Department of Mathematics, University of Pennsylvania, Philadelphia, PA19104-6395, USA (harbater@math.upenn.edu; hartmann@math.upenn.edu; pop@math.upenn.edu)
Florian Pop
Affiliation:
Department of Mathematics, University of Pennsylvania, Philadelphia, PA19104-6395, USA (harbater@math.upenn.edu; hartmann@math.upenn.edu; pop@math.upenn.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We solve the inverse differential Galois problem over differential fields with a large field of constants of infinite transcendence degree over 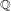$\mathbb{Q}$. More generally, we show that over such a field, every split differential embedding problem can be solved. In particular, we solve the inverse differential Galois problem and all split differential embedding problems over 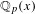$\mathbb{Q}_{p}(x)$.

Keywords

Picard–Vessiot theorylarge fieldsinverse differential Galois problemembedding problemslinear algebraic groups

MSC classification

Primary: 12H05: Differential algebra 12E30: Field arithmetic 20G15: Linear algebraic groups over arbitrary fields
Secondary: 12F12: Inverse Galois theory 14H25: Arithmetic ground fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 6 , November 2021 , pp. 1931 - 1946
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was funded by the Deutsche Forschungsgemeinschaft (DFG) – grant MA6868/1-1 and by the Alexander von Humboldt foundation through a Feodor Lynen fellowship. The second and third authors were supported by NSF collaborative FRG grant DMS-1463733 and NSF grant DMS-1805439; additional support was provided by NSF collaborative FRG grant DMS-1265290 (DH) and a Simons Fellowship (JH). The fourth author was supported by NSF collaborative FRG grant DMS-1265290.

References

Amano, K. and Masuoka, A., Picard–Vessiot extensions of Artinian simple module algebras, J. Algebra 285(2) (2005), 743–767.Google Scholar
André, Y., Différentielles non-commutatives et théorie de Galois différentielle ou aux différences, Ann. Sci. Éc. Norm. Supér. 34 (2001), 685–739.Google Scholar
Bachmayr, A., Harbater, D. and Hartmann, J., Differential Galois groups over Laurent series fields, Proc. Lond. Math. Soc. (3) 112(3) (2016), 455–476.Google Scholar
Bachmayr, A., Harbater, D. and Hartmann, J., Differential embedding problems over Laurent series fields, J. Algebra 513 (2018), 99–112.Google Scholar
Bachmayr, A., Harbater, D., Hartmann, J. and Wibmer, M., Differential embedding problems over complex function fields, Doc. Math. 23 (2018), 241–291.Google Scholar
Crespo, T., Hajto, Z. and van der Put, M., Real and p-adic Picard–Vessiot fields, Math. Ann. 365 (2016), 93–103.Google Scholar
Dyckerhoff, T., The inverse problem of differential Galois theory over the field $\mathbb{R}(z)$ , Manuscript, 2008, arXiv:0802.2897.Google Scholar
Ernst, S., Iterative differential embedding problems in positive characteristic, J. Algebra 402 (2014), 544–564.Google Scholar
Fehm, A., Embeddings of function fields into ample fields, Manuscripta Math. 134 (2011), 533–544.Google Scholar
Fried, M. D. and Jarden, M., Field Arithmetic, 3rd edn, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], Volume 11 (Springer, Berlin, 2008). Revised by Jarden.Google Scholar
Haran, D. and Jarden, M., Regular split embedding problems over complete valued fields, Forum Math. 10(3) (1998), 329–351.Google Scholar
Harbater, D., Fundamental groups and embedding problems in characteristic p, in Recent Developments in the Inverse Galois Problem (Seattle, WA, 1993), Contemporary Mathematics, Volume 186, pp. 353–369 (American Mathematical Society, Providence, RI, 1995).Google Scholar
Harbater, D. and Stevenson, K. F., Local Galois theory in dimension two, Adv. Math. 198(2) (2005), 623–653.Google Scholar
Hartmann, J., On the inverse problem in differential Galois theory, J. Reine Angew. Math. 586 (2005), 21–44.Google Scholar
Hrushovski, E., Computing the Galois group of a linear differential equation, in Differential Galois Theory (Bedlewo, 2001), Banach Center Publ., Volume 58, pp. 97–138 (Polish Acad. Sci. Inst. Math., Warsaw, 2002).Google Scholar
León Sánchez, O. and Pillay, A., Some definable Galois theory and examples, Bull. Symb. Log. 23 (2017), 145–159.Google Scholar
Matzat, B. H. and van der Put, M., Constructive differential Galois theory, in Galois Groups and Fundamental Groups, Mathematical Sciences Research Institute Publications, Volume 41, pp. 425–467 (2003).Google Scholar
Maurischat, A., Galois theory for iterative connections and nonreduced Galois groups, Trans. Amer. Math. Soc. 362(10) (2010), 5411–5453.Google Scholar
Oberlies, T., Einbettungsprobleme in der Differentialgaloistheorie. Dissertation, Universität Heidelberg, 2003. Available at http://www.ub.uni-heidelberg.de/archiv/4550.Google Scholar
Pop, F., Étale Galois covers of affine smooth curves. The geometric case of a conjecture of Shafarevich. On Abhyankar’s conjecture, Invent. Math. 120(3) (1995), 555–578.Google Scholar
Pop, F., Embedding problems over large fields, Ann. of Math. (2) 144(1) (1996), 1–34.Google Scholar
Pop, F., Henselian implies large, Ann. of Math. (2) 172 (2010), 2183–2195.Google Scholar
Pop, F., Little survey on large fields—old & new, in Valuation Theory in Interaction, EMS Ser. Congr. Rep., pp. 432–463 (Eur. Math. Soc., Zürich, 2014).Google Scholar
van der Put, M. and Singer, M. F., Galois Theory of Linear Differential Equations, Grundlehren der Mathematischen Wissenschaften, Volume 328 (Springer, Berlin, 2003).Google Scholar
Serre, J.-P., Galois Cohomology, Corrected reprint of the 1997 English edition, Springer Monographs in Mathematics (Springer, Berlin, 2002).Google Scholar