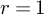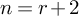1 Introduction
Having fixed positive integers r and s and setting
![]() $g=rs+s$
and
$g=rs+s$
and
![]() $d=rs+r$
, in a celebrated paper [Reference Castelnuovo3], Castelnuovo computed the number of linear series of type
$d=rs+r$
, in a celebrated paper [Reference Castelnuovo3], Castelnuovo computed the number of linear series of type
![]() $g^r_d$
on a general curve C of genus g. By degeneration to a g-nodal rational curve, he argued that this number equals the degree of the Grassmannian
$g^r_d$
on a general curve C of genus g. By degeneration to a g-nodal rational curve, he argued that this number equals the degree of the Grassmannian
![]() $\operatorname {\mathrm {Gr}}(r+1,d+1)$
in its Plücker embedding, that is,
$\operatorname {\mathrm {Gr}}(r+1,d+1)$
in its Plücker embedding, that is,
 $$ \begin{align*}g!\cdot\frac{1!\cdot 2! \cdot \cdots \cdot r!}{s!\cdot(s+1)! \cdot \cdots \cdot (s+r)!}. \end{align*} $$
$$ \begin{align*}g!\cdot\frac{1!\cdot 2! \cdot \cdots \cdot r!}{s!\cdot(s+1)! \cdot \cdots \cdot (s+r)!}. \end{align*} $$
A rigorous modern presentation of Castelnuovo’s argumentFootnote 1 was first carried out by Griffiths and Harris [Reference Griffiths and Harris11]. More generally, the theory of limit linear series developed by Eisenbud and Harris [Reference Eisenbud and Harris6, Reference Eisenbud and Harris7] allows one to compute the number of linear series on a general curve with ramification conditions imposed at fixed marked points, see also [Reference Osserman18] for a more recent treatment.
Motivated by two recent papers of Tevelev [Reference Tevelev19] and Cela, Pandharipande and Schmitt [Reference Cela, Pandharipande and Schmitt5], we consider a variant of this problem, where we impose incidence conditions on the corresponding maps to projective spaces. Let
![]() $[C,x_1,\ldots ,x_n]\in \mathcal {M}_{g,n}$
be a general n-pointed complex curve of genus g. We denote by
$[C,x_1,\ldots ,x_n]\in \mathcal {M}_{g,n}$
be a general n-pointed complex curve of genus g. We denote by
![]() $G^r_d(C)$
the variety of linear systems
$G^r_d(C)$
the variety of linear systems
![]() $\ell =(L,V)$
of type
$\ell =(L,V)$
of type
![]() $g^r_d$
on C. A general
$g^r_d$
on C. A general
![]() $\ell \in G^r_d(C)$
corresponds to a regular map
$\ell \in G^r_d(C)$
corresponds to a regular map
![]() $\phi _{\ell }\colon C\rightarrow \mathbb P^r$
. Evaluation at the points
$\phi _{\ell }\colon C\rightarrow \mathbb P^r$
. Evaluation at the points
![]() $x_1, \ldots , x_n$
induces a rational map:
$x_1, \ldots , x_n$
induces a rational map:
to the moduli spaces of n points in
![]() $\mathbb {P}^r$
.Footnote
2
We study the degree
$\mathbb {P}^r$
.Footnote
2
We study the degree
![]() $L_{g,r,d}$
of the map
$L_{g,r,d}$
of the map
![]() $\mathrm {ev}_{(x_1, \ldots , x_n)}$
in the case when this map is generically finite and both spaces have nonnegative dimension. Since
$\mathrm {ev}_{(x_1, \ldots , x_n)}$
in the case when this map is generically finite and both spaces have nonnegative dimension. Since
![]() $G^r_d(C)$
is a smooth variety of dimension
$G^r_d(C)$
is a smooth variety of dimension
![]() $\rho (g,r,d)=g-(r+1)(g-d+r)$
, whereas
$\rho (g,r,d)=g-(r+1)(g-d+r)$
, whereas
![]() $\mbox {dim}(P_r^n)=rn-r^2-2r$
as long as
$\mbox {dim}(P_r^n)=rn-r^2-2r$
as long as
![]() $n\geq r+2$
, one expects
$n\geq r+2$
, one expects
![]() $\mathrm {ev}_{(x_1, \ldots , x_n)}$
to be generically finite precisely when:
$\mathrm {ev}_{(x_1, \ldots , x_n)}$
to be generically finite precisely when:
Equivalently,
![]() $L_{g,r,d}$
may be understood as the degree of the morphism:
$L_{g,r,d}$
may be understood as the degree of the morphism:
where
![]() $\mathcal {M}_{g,n}(\mathbb {P}^r,d)$
is the moduli space of degree d maps
$\mathcal {M}_{g,n}(\mathbb {P}^r,d)$
is the moduli space of degree d maps
![]() $f:C\to \mathbb {P}^r$
, with smooth domain and distinct marked points
$f:C\to \mathbb {P}^r$
, with smooth domain and distinct marked points
![]() $x_1,\ldots ,x_n\in C$
, and the map
$x_1,\ldots ,x_n\in C$
, and the map
![]() $\tau $
remembers the pointed domain and the images of the
$\tau $
remembers the pointed domain and the images of the
![]() $x_i$
under f. Again, the map
$x_i$
under f. Again, the map
![]() $\tau $
is expected to be generically finite exactly when (2) holds, and Brill-Noether theory guarantees that this is indeed the case as long as
$\tau $
is expected to be generically finite exactly when (2) holds, and Brill-Noether theory guarantees that this is indeed the case as long as
![]() $d>0$
.
$d>0$
.
If
![]() $y_1,\ldots ,y_n\in \mathbb {P}^r$
are general points,
$y_1,\ldots ,y_n\in \mathbb {P}^r$
are general points,
![]() $L_{g,r,d}$
counts the number of morphisms
$L_{g,r,d}$
counts the number of morphisms
![]() $f\colon C\to \mathbb {P}^r$
of degree d satisfying
$f\colon C\to \mathbb {P}^r$
of degree d satisfying
![]() $f(x_i)=y_i$
for
$f(x_i)=y_i$
for
![]() $i=1, \ldots , n$
. When the points
$i=1, \ldots , n$
. When the points
![]() $y_i$
are considered up to projective equivalence, these incidence conditions are intrinsic to
$y_i$
are considered up to projective equivalence, these incidence conditions are intrinsic to
![]() $\ell $
. For large d, it turns out there is a very simple formula for this degree:
$\ell $
. For large d, it turns out there is a very simple formula for this degree:
Theorem 1.1. Suppose
![]() $d\ge rg+r$
, or equivalently,
$d\ge rg+r$
, or equivalently,
![]() $n\ge d+2$
. Then:
$n\ge d+2$
. Then:
We remark that the hypothesis
![]() $n\ge d+2$
is automatically satisfied whenever
$n\ge d+2$
is automatically satisfied whenever
![]() $g\le 1$
. Indeed, if instead
$g\le 1$
. Indeed, if instead
![]() $n\le d+1$
and
$n\le d+1$
and
![]() $g\le 1$
, then
$g\le 1$
, then
![]() $d+1\ge n=d+1+\frac {d}{r}-g\ge d+\frac {d}{r}$
, hence,
$d+1\ge n=d+1+\frac {d}{r}-g\ge d+\frac {d}{r}$
, hence,
![]() $n\le d+1\le r+1$
, a contradiction. On the other hand, we will also see that the inequality
$n\le d+1\le r+1$
, a contradiction. On the other hand, we will also see that the inequality
![]() $d\ge rg+r$
is sharp in the sense that
$d\ge rg+r$
is sharp in the sense that
![]() $L_{g,r,d}=(r+1)^{g}-(d+1) $
when
$L_{g,r,d}=(r+1)^{g}-(d+1) $
when
![]() $d=rg$
, see Remark 3.4.
$d=rg$
, see Remark 3.4.
When
![]() $r=1$
, the special case
$r=1$
, the special case
![]() $d=g+1$
was studied under the guise of scattering amplitudes by Tevelev [Reference Tevelev19], who found the strikingly simple formula
$d=g+1$
was studied under the guise of scattering amplitudes by Tevelev [Reference Tevelev19], who found the strikingly simple formula
![]() $L_{g,1,g+1}=2^g$
. This raised the possibility, confirmed by Theorem 1.1, that in the range when d is relatively large, the degree
$L_{g,1,g+1}=2^g$
. This raised the possibility, confirmed by Theorem 1.1, that in the range when d is relatively large, the degree
![]() $L_{g,r,d}$
has a simple expression. Using Hurwitz space techniques, Cela, Pandharipande and Schmitt [Reference Cela, Pandharipande and Schmitt5] obtained general formulas for
$L_{g,r,d}$
has a simple expression. Using Hurwitz space techniques, Cela, Pandharipande and Schmitt [Reference Cela, Pandharipande and Schmitt5] obtained general formulas for
![]() $L_{g,1,d}$
, which they called Tevelev degrees; in particular, when
$L_{g,1,d}$
, which they called Tevelev degrees; in particular, when
![]() $d\ge g+1$
, they found again,
$d\ge g+1$
, they found again,
![]() $L_{g,1,d}=2^g$
.
$L_{g,1,d}=2^g$
.
The result of Theorem 1.1 can be compared to a certain virtual count of Bertram, Daskalopoulous and Wentworth [Reference Bertram, Daskalopoulos and Wentworth1, Theorem 2.9] in the range
![]() $d>2g-2$
, predating the theory of virtual fundamental classes on moduli spaces of stable maps.
$d>2g-2$
, predating the theory of virtual fundamental classes on moduli spaces of stable maps.
When either
![]() $r=1$
or
$r=1$
or
![]() $n=r+2$
, or under the hypotheses of Theorem 1.1, we obtain a more general formula for
$n=r+2$
, or under the hypotheses of Theorem 1.1, we obtain a more general formula for
![]() $L_{g,r,d}$
in terms of Schubert calculus. For a positive integer a, we recall the notation
$L_{g,r,d}$
in terms of Schubert calculus. For a positive integer a, we recall the notation
![]() $\sigma _a$
for the class of the special Schubert cycle of codimension a consisting of those
$\sigma _a$
for the class of the special Schubert cycle of codimension a consisting of those
![]() $(r+1)$
-planes
$(r+1)$
-planes
![]() $V\in \operatorname {\mathrm {Gr}}(r+1,d+1)$
meeting a fixed subspace
$V\in \operatorname {\mathrm {Gr}}(r+1,d+1)$
meeting a fixed subspace
![]() $W\subseteq \mathbb C^{d+1}$
of dimension
$W\subseteq \mathbb C^{d+1}$
of dimension
![]() $d-a$
. We also recall that
$d-a$
. We also recall that
![]() $\sigma _{1^r}$
denotes the class of the special Schubert cycle of codimension r consisting of those
$\sigma _{1^r}$
denotes the class of the special Schubert cycle of codimension r consisting of those
![]() $(r+1)$
-planes
$(r+1)$
-planes
![]() $V\in \operatorname {\mathrm {Gr}}(r+1,d+1)$
whose intersection with a fixed codimension 2 linear subspace
$V\in \operatorname {\mathrm {Gr}}(r+1,d+1)$
whose intersection with a fixed codimension 2 linear subspace
![]() $U\subseteq \mathbb C^{d+1}$
has dimension at least r. Our main result is as follows:
$U\subseteq \mathbb C^{d+1}$
has dimension at least r. Our main result is as follows:
Theorem 1.2. Suppose that either:
-
•
 $d\ge rg+r$
, (i.e. the same hypothesis as in Theorem 1.1),
$d\ge rg+r$
, (i.e. the same hypothesis as in Theorem 1.1), -
•
 $d=r+\frac {rg}{r+1}$
(in which case,
$d=r+\frac {rg}{r+1}$
(in which case,
 $n=r+2$
), or
$n=r+2$
), or -
•
 $r=1$
.
$r=1$
.
In each of these cases,
 $$ \begin{align*} L_{g,r,d}=\int_{\operatorname{\mathrm{Gr}}(r+1,d+1)}\sigma_{1^r}^{g}\cdot\left[ \sum_{\alpha_0+\cdots+\alpha_{r}=(r+1)(d-r)-rg}\left(\prod_{i=0}^{r}\sigma_{\alpha_i}\right)\right]. \end{align*} $$
$$ \begin{align*} L_{g,r,d}=\int_{\operatorname{\mathrm{Gr}}(r+1,d+1)}\sigma_{1^r}^{g}\cdot\left[ \sum_{\alpha_0+\cdots+\alpha_{r}=(r+1)(d-r)-rg}\left(\prod_{i=0}^{r}\sigma_{\alpha_i}\right)\right]. \end{align*} $$
In particular, comparing Theorem 1.1 with 1.2 when
![]() $d\ge rg+r$
yields a nontrivial combinatorial identityFootnote
3
.
$d\ge rg+r$
yields a nontrivial combinatorial identityFootnote
3
.
In the second case, in which d is as small as possible, we have
![]() $(r+1)(d-r)=gr$
, so the second term is interpreted to be 1, and Theorem 1.2 recovers Castelnuovo’s formula for
$(r+1)(d-r)=gr$
, so the second term is interpreted to be 1, and Theorem 1.2 recovers Castelnuovo’s formula for
![]() $s=g/(r+1)$
. On the other hand, when
$s=g/(r+1)$
. On the other hand, when
![]() $gr>(r+1)(d-r)$
(equivalently,
$gr>(r+1)(d-r)$
(equivalently,
![]() $n<r+2$
), the summation is interpreted to be zero, so that
$n<r+2$
), the summation is interpreted to be zero, so that
![]() $L_{g,r,d}=0$
. Indeed, this corresponds to the case
$L_{g,r,d}=0$
. Indeed, this corresponds to the case
![]() $\dim G^{r}_{d}(C)=\dim (P_r^n)<0$
, in which we find no such morphisms
$\dim G^{r}_{d}(C)=\dim (P_r^n)<0$
, in which we find no such morphisms
![]() $f\colon C\to \mathbb {P}^r$
.
$f\colon C\to \mathbb {P}^r$
.
The case of intermediate d when
![]() $r>1$
is the most subtle, and will be addressed in later work.
$r>1$
is the most subtle, and will be addressed in later work.
For
![]() $r=1$
, Theorem 1.2, via Giambelli’s formula, yields the following explicit formulas for
$r=1$
, Theorem 1.2, via Giambelli’s formula, yields the following explicit formulas for
![]() $L_{g,1,d}$
, the last of which agrees with the results of [Reference Cela, Pandharipande and Schmitt5, Theorem 6], see Proposition 3.7 for details.
$L_{g,1,d}$
, the last of which agrees with the results of [Reference Cela, Pandharipande and Schmitt5, Theorem 6], see Proposition 3.7 for details.
 $$ \begin{align*} L_{g,1,d}&=\sum_{\alpha_0+\alpha_1=2d-2-g}\int_{\operatorname{\mathrm{Gr}}(2,d+1)} \sigma_1^g\cdot \sigma_{\alpha_0}\cdot \sigma_{\alpha_1}\\ &= \sum_{i=0}^{\bigl \lfloor \frac{2d-g-2}{2}\bigr \rfloor} \frac{(2d-g-2i-1)^2}{g+1} {g+1\choose d-i}\\ &=2^g-2\sum_{i=0}^{g-d-1}\binom{g}{i}+(g-d-1)\binom{g}{g-d}+(d-g-1)\binom{g}{g-d+1}. \end{align*} $$
$$ \begin{align*} L_{g,1,d}&=\sum_{\alpha_0+\alpha_1=2d-2-g}\int_{\operatorname{\mathrm{Gr}}(2,d+1)} \sigma_1^g\cdot \sigma_{\alpha_0}\cdot \sigma_{\alpha_1}\\ &= \sum_{i=0}^{\bigl \lfloor \frac{2d-g-2}{2}\bigr \rfloor} \frac{(2d-g-2i-1)^2}{g+1} {g+1\choose d-i}\\ &=2^g-2\sum_{i=0}^{g-d-1}\binom{g}{i}+(g-d-1)\binom{g}{g-d}+(d-g-1)\binom{g}{g-d+1}. \end{align*} $$
Here, we adopt the convention that
![]() $\binom {g}{j}=0$
when
$\binom {g}{j}=0$
when
![]() $j<0$
, so in particular, we have again that
$j<0$
, so in particular, we have again that
![]() $L_{g,1,d}=2^g$
when
$L_{g,1,d}=2^g$
when
![]() $d\ge g+1$
.
$d\ge g+1$
.
To prove Theorems 1.1 and 1.2, we proceed via a standard degeneration to a flag curve consisting of a rational spine and
![]() $g+1$
tails, one of which being rational and on which all the marked points specialise, the remaining g tails being elliptic curves. We reduce to a concrete problem in genus zero in §2, and then handle this problem via Schubert calculus in §3; care needs to be taken to avoid degenerate solutions, particularly excess contributions from constant maps
$g+1$
tails, one of which being rational and on which all the marked points specialise, the remaining g tails being elliptic curves. We reduce to a concrete problem in genus zero in §2, and then handle this problem via Schubert calculus in §3; care needs to be taken to avoid degenerate solutions, particularly excess contributions from constant maps
![]() $f\colon \mathbb {P}^1\to \mathbb {P}^r$
obtained from linear series with base points at some of the points
$f\colon \mathbb {P}^1\to \mathbb {P}^r$
obtained from linear series with base points at some of the points
![]() $x_i$
. Because such excess contributions in our setup persist when the hypotheses of Theorem 1.2 are not satisfied (see Remark 3.6), the general computation of
$x_i$
. Because such excess contributions in our setup persist when the hypotheses of Theorem 1.2 are not satisfied (see Remark 3.6), the general computation of
![]() $L_{g,r,d}$
remains open.
$L_{g,r,d}$
remains open.
Our method in the case
![]() $r=1$
also allows us to recompute the more general counts of Cela, Pandharipande and Schmitt [Reference Cela, Pandharipande and Schmitt5], where some points of the source curve are constrained to have the same image. If
$r=1$
also allows us to recompute the more general counts of Cela, Pandharipande and Schmitt [Reference Cela, Pandharipande and Schmitt5], where some points of the source curve are constrained to have the same image. If
![]() $r=1$
and
$r=1$
and
![]() $1\le k\le d,n$
, let
$1\le k\le d,n$
, let
![]() $L^{\prime }_{g,d,k}$
be the number of morphisms
$L^{\prime }_{g,d,k}$
be the number of morphisms
![]() $f\colon C\to \mathbb {P}^1$
as before, but where we take
$f\colon C\to \mathbb {P}^1$
as before, but where we take
![]() $y_1=y_2=\cdots =y_k$
, and the
$y_1=y_2=\cdots =y_k$
, and the
![]() $y_i$
otherwise general. (Note that our indexing differs from that of [Reference Cela, Pandharipande and Schmitt5], where d is written as
$y_i$
otherwise general. (Note that our indexing differs from that of [Reference Cela, Pandharipande and Schmitt5], where d is written as
![]() $g+1+\ell $
for some
$g+1+\ell $
for some
![]() $\ell \in \mathbb {Z}$
and k is called r, whereas we have reserved the variable r to denote the dimension of the target projective space.) We find:
$\ell \in \mathbb {Z}$
and k is called r, whereas we have reserved the variable r to denote the dimension of the target projective space.) We find:
Theorem 1.3.
 $$ \begin{align*} L^{\prime}_{g,d,k}\,&=\int_{\operatorname{\mathrm{Gr}}(2,d+1)}\sigma_1^g\sigma_{k-1}\cdot\left[\sum_{i+j=2(d-1)-g-(k-1)} \sigma_{i}\sigma_j\right]\\&\quad-\int_{\operatorname{\mathrm{Gr}}(2,d)}\sigma_1^g\sigma_{k-2}\cdot\left[\sum_{i+j=2(d-2)-g-(k-2)}\sigma_{i}\sigma_j\right]. \end{align*} $$
$$ \begin{align*} L^{\prime}_{g,d,k}\,&=\int_{\operatorname{\mathrm{Gr}}(2,d+1)}\sigma_1^g\sigma_{k-1}\cdot\left[\sum_{i+j=2(d-1)-g-(k-1)} \sigma_{i}\sigma_j\right]\\&\quad-\int_{\operatorname{\mathrm{Gr}}(2,d)}\sigma_1^g\sigma_{k-2}\cdot\left[\sum_{i+j=2(d-2)-g-(k-2)}\sigma_{i}\sigma_j\right]. \end{align*} $$
The second term is taken to be zero when
![]() $k=1$
. Note that
$k=1$
. Note that
![]() $L^{\prime }_{g,d,1}=L_{g,1,d}$
, so Theorem 1.3 agrees with Theorem 1.2 in the case
$L^{\prime }_{g,d,1}=L_{g,1,d}$
, so Theorem 1.3 agrees with Theorem 1.2 in the case
![]() $r=1$
. From here, the formulas of [Reference Cela, Pandharipande and Schmitt5, Theorem 6] can be recovered by recursion, see Corollary 5.1. We sketch the proof of Theorem 1.3 in §5.1; a more general statement with detailed proofs is given in [Reference Cela and Lian4, §6].
$r=1$
. From here, the formulas of [Reference Cela, Pandharipande and Schmitt5, Theorem 6] can be recovered by recursion, see Corollary 5.1. We sketch the proof of Theorem 1.3 in §5.1; a more general statement with detailed proofs is given in [Reference Cela and Lian4, §6].
Finally, we remark that the degeneration technique also allows one to impose ramification conditions at additional fixed points
![]() $p_1,\ldots ,p_m\in C$
, see §5.2.
$p_1,\ldots ,p_m\in C$
, see §5.2.
Relation to other work. We discuss results related to this circle of ideas that appeared after our paper was published on arXiv. The count of Theorem 1.1 agrees with a virtual count of maps
![]() $C\to \mathbb {P}^r$
in Gromov-Witten theory as computed by Buch and Pandharipande [Reference Buch and Pandharipande2], the so-called virtual Tevelev degrees of
$C\to \mathbb {P}^r$
in Gromov-Witten theory as computed by Buch and Pandharipande [Reference Buch and Pandharipande2], the so-called virtual Tevelev degrees of
![]() $\mathbb {P}^r$
. We consider the map
$\mathbb {P}^r$
. We consider the map
![]() $\tau \colon \overline {\mathcal {M}}_{g,n}(\mathbb {P}^r,d)\to \overline {\mathcal {M}}_{g,n}\times (\mathbb {P}^r)^n$
be the map remembering
$\tau \colon \overline {\mathcal {M}}_{g,n}(\mathbb {P}^r,d)\to \overline {\mathcal {M}}_{g,n}\times (\mathbb {P}^r)^n$
be the map remembering
![]() $[(C,x_1,\ldots ,x_n)]$
and the points
$[(C,x_1,\ldots ,x_n)]$
and the points
![]() $y_i=f(x_i)$
. Then, under assumption (2), we have [Reference Buch and Pandharipande2, §1.3]:
$y_i=f(x_i)$
. Then, under assumption (2), we have [Reference Buch and Pandharipande2, §1.3]:
for all d. When
![]() $d<rg+r$
, the virtual count includes excess contributions we wish to exclude in our counts
$d<rg+r$
, the virtual count includes excess contributions we wish to exclude in our counts
![]() $L_{g,r,d}$
.
$L_{g,r,d}$
.
More generally, when
![]() $\mathbb {P}^r$
is replaced by an arbitrary target variety X, the corresponding virtual degrees are expressed in terms of the quantum cohomology of X (see [Reference Buch and Pandharipande2, Theorem 1.3]). It is expected that for all Fano varieties X, the virtual count of maps of sufficiently large degree is enumerative, as in Theorem 1.1, see [Reference Lian and Pandharipande13] for partial results in this direction.
$\mathbb {P}^r$
is replaced by an arbitrary target variety X, the corresponding virtual degrees are expressed in terms of the quantum cohomology of X (see [Reference Buch and Pandharipande2, Theorem 1.3]). It is expected that for all Fano varieties X, the virtual count of maps of sufficiently large degree is enumerative, as in Theorem 1.1, see [Reference Lian and Pandharipande13] for partial results in this direction.
2 Reduction to genus zero
In this section, we reduce the enumerative problem to genus zero via a standard limit linear series degeneration, see for example [Reference Lian12, Reference Osserman18]. We begin by recalling some notation, while assuming throughout some familiarity with basics of the theory of limit linear series [Reference Eisenbud and Harris7].
We recall the usual notation for Schubert cycles in the Grassmannian
![]() $\operatorname {\mathrm {Gr}}(r+1,d+1):=\operatorname {\mathrm {Gr}}(r+1,V)$
, where V is a
$\operatorname {\mathrm {Gr}}(r+1,d+1):=\operatorname {\mathrm {Gr}}(r+1,V)$
, where V is a
![]() $(d+1)$
-dimensional vector space, following [Reference Eisenbud and Harris9, §4]. For a nonincreasing sequence
$(d+1)$
-dimensional vector space, following [Reference Eisenbud and Harris9, §4]. For a nonincreasing sequence
![]() $\mu :=(\mu _0\geq \mu _1\geq \cdots \geq \mu _r)$
and a flag
$\mu :=(\mu _0\geq \mu _1\geq \cdots \geq \mu _r)$
and a flag
![]() ${\textbf F}: V=V_{d+1}\supset V_d\supset \ldots \supset V_1\supset V_0=0$
, we introduce the Schubert cycle:
${\textbf F}: V=V_{d+1}\supset V_d\supset \ldots \supset V_1\supset V_0=0$
, we introduce the Schubert cycle:
Note that
![]() $\mbox {codim}\bigl (\sigma _{\mu }, \operatorname {\mathrm {Gr}}(r+1,d+1)\bigr )=|\mu |=\mu _0+\cdots +\mu _r$
. If
$\mbox {codim}\bigl (\sigma _{\mu }, \operatorname {\mathrm {Gr}}(r+1,d+1)\bigr )=|\mu |=\mu _0+\cdots +\mu _r$
. If
![]() $\mu =(1,\ldots , 1, 0)=:1^r$
, in projective terms,
$\mu =(1,\ldots , 1, 0)=:1^r$
, in projective terms,
![]() $\Sigma _{1^r}$
consists of r-dimensional subspaces
$\Sigma _{1^r}$
consists of r-dimensional subspaces
![]() $L=\mathbb P(\Lambda )\subset \mathbb P(V)\cong \mathbb P^d$
intersecting a fixed codimension
$L=\mathbb P(\Lambda )\subset \mathbb P(V)\cong \mathbb P^d$
intersecting a fixed codimension
![]() $2$
subspace along an r-dimensional locus. We set
$2$
subspace along an r-dimensional locus. We set
![]() $\sigma _{\mu }:=[\Sigma _{\mu }]\in \operatorname {{\mathrm {CH}}}^{|\mu |}\bigl (\operatorname {\mathrm {Gr}}(r+1,g+1)\bigr )$
.
$\sigma _{\mu }:=[\Sigma _{\mu }]\in \operatorname {{\mathrm {CH}}}^{|\mu |}\bigl (\operatorname {\mathrm {Gr}}(r+1,g+1)\bigr )$
.
For a smooth curve C and a linear series
![]() $\ell =(L,V)\in G^r_d(C)$
, we denote by:
$\ell =(L,V)\in G^r_d(C)$
, we denote by:
the ramification sequence at a point
![]() $p\in C$
. Keeping with the tradition of [Reference Eisenbud and Harris7] or [Reference Griffiths and Harris11], we write ramification indices of linear series nondecreasingly, whereas indices indexing Schubert cycles are written nonincreasingly. We formalise this practice as follows:
$p\in C$
. Keeping with the tradition of [Reference Eisenbud and Harris7] or [Reference Griffiths and Harris11], we write ramification indices of linear series nondecreasingly, whereas indices indexing Schubert cycles are written nonincreasingly. We formalise this practice as follows:
Definition 2.1. For any partition
![]() $\mu =(\mu _0\geq \mu _1\geq \cdots \geq \mu _r)$
, denote by
$\mu =(\mu _0\geq \mu _1\geq \cdots \geq \mu _r)$
, denote by
![]() $\overline {\mu }$
the tuple of components of
$\overline {\mu }$
the tuple of components of
![]() $\mu $
in reverse (increasing) order, that is,
$\mu $
in reverse (increasing) order, that is,
![]() $\overline {\mu }=(\mu _r,\ldots ,\mu _0)$
.
$\overline {\mu }=(\mu _r,\ldots ,\mu _0)$
.
We introduce the proper stack of limit linear series of type
![]() $g^r_d$
:
$g^r_d$
:
over the moduli space
![]() $\mathcal {M}_g^{\mathrm {ct}}$
of curves of compact type. For a curve C of compact type, we denote by
$\mathcal {M}_g^{\mathrm {ct}}$
of curves of compact type. For a curve C of compact type, we denote by
![]() $\overline {G}^r_d(C)$
the variety of limit linear series on C. For pairwise distinct smooth points
$\overline {G}^r_d(C)$
the variety of limit linear series on C. For pairwise distinct smooth points
![]() $p_1, \ldots , p_n\in C_{\mathrm {reg}}$
and Schubert indices
$p_1, \ldots , p_n\in C_{\mathrm {reg}}$
and Schubert indices
![]() $\alpha ^i=\bigl (0\leq \alpha _0^i\leq \cdots \leq \alpha _r^i\leq d-r\bigr )$
, where
$\alpha ^i=\bigl (0\leq \alpha _0^i\leq \cdots \leq \alpha _r^i\leq d-r\bigr )$
, where
![]() $i=1, \ldots , n$
, we set:
$i=1, \ldots , n$
, we set:
viewed as a generalised degeneracy locus of expected dimension:
 $$ \begin{align} \rho(g,r,d, \alpha^1, \ldots, \ldots, \alpha^n):=g-(r+1)(g-d+r)-\sum_{i=1}^n \sum_{j=0}^r \alpha_j^i. \end{align} $$
$$ \begin{align} \rho(g,r,d, \alpha^1, \ldots, \ldots, \alpha^n):=g-(r+1)(g-d+r)-\sum_{i=1}^n \sum_{j=0}^r \alpha_j^i. \end{align} $$
We now consider a degeneration to the following flag curve of genus g, already considered in [Reference Eisenbud and Harris7]. Let
![]() $[C_0, x_1, \ldots , x_n]$
be the n-pointed genus g curve of compact type consisting of a rational spine
$[C_0, x_1, \ldots , x_n]$
be the n-pointed genus g curve of compact type consisting of a rational spine
![]() $R_{\operatorname {\mathrm {sp}}}$
to which general elliptic tails
$R_{\operatorname {\mathrm {sp}}}$
to which general elliptic tails
![]() $E_1,\ldots ,E_g$
are attached at general points
$E_1,\ldots ,E_g$
are attached at general points
![]() $p_1, \ldots , p_g\in R_{\operatorname {\mathrm {sp}}}$
, respectively, and a further rational component
$p_1, \ldots , p_g\in R_{\operatorname {\mathrm {sp}}}$
, respectively, and a further rational component
![]() $R_0$
also attached at a general point
$R_0$
also attached at a general point
![]() $x_0$
of
$x_0$
of
![]() $R_{\operatorname {\mathrm {sp}}}$
. The marked points
$R_{\operatorname {\mathrm {sp}}}$
. The marked points
![]() $x_1,\ldots ,x_n$
specialise to general points of
$x_1,\ldots ,x_n$
specialise to general points of
![]() $R_0$
.
$R_0$
.
Let
![]() $\mathcal {C}\rightarrow (B, b_0)$
be the versal deformation space of
$\mathcal {C}\rightarrow (B, b_0)$
be the versal deformation space of
![]() $[C_0, x_1, \ldots , x_n]$
and denote by
$[C_0, x_1, \ldots , x_n]$
and denote by
![]() $\tau _1, \ldots , \tau _n \colon B\rightarrow \mathcal {C}$
the sections corresponding to the n marked points. We may assume that each point of B parametrises an n-pointed curve of genus g of compact type. We further consider the induced moduli map
$\tau _1, \ldots , \tau _n \colon B\rightarrow \mathcal {C}$
the sections corresponding to the n marked points. We may assume that each point of B parametrises an n-pointed curve of genus g of compact type. We further consider the induced moduli map
![]() $B\rightarrow \mathcal {M}_g^{\mathrm {ct}}$
forgetting the markings and let:
$B\rightarrow \mathcal {M}_g^{\mathrm {ct}}$
forgetting the markings and let:
be the corresponding family of limit linear series and consider the evaluation map:
where
![]() $\phi _{\ell }$
denotes the rational map to
$\phi _{\ell }$
denotes the rational map to
![]() $\mathbb P^r$
corresponding to the aspect of the limit linear series
$\mathbb P^r$
corresponding to the aspect of the limit linear series
![]() $\ell $
on the component of
$\ell $
on the component of
![]() $C_b$
on which all the marked points
$C_b$
on which all the marked points
![]() $\tau _1(b), \ldots , \tau _n(b)$
lie.
$\tau _1(b), \ldots , \tau _n(b)$
lie.
Using [Reference Eisenbud and Harris8, Theorem 1.1], it follows that
![]() $\widetilde {\mathcal {G}}^r_d/B$
is smooth of dimension
$\widetilde {\mathcal {G}}^r_d/B$
is smooth of dimension
![]() $3g-3+n+\rho (g,r,d)$
over B and every limit linear series on
$3g-3+n+\rho (g,r,d)$
over B and every limit linear series on
![]() $C_0$
smooths to a linear series on a neighboring smooth curve. It follows that
$C_0$
smooths to a linear series on a neighboring smooth curve. It follows that
![]() $\mbox {deg}(\mathrm {ev})=L_{d,g,r}$
. We will determine this degree by looking at the scheme-theoretic fibre
$\mbox {deg}(\mathrm {ev})=L_{d,g,r}$
. We will determine this degree by looking at the scheme-theoretic fibre
![]() $\mathrm {ev}^{-1}(b_0, y_1, \ldots , y_n)$
, where
$\mathrm {ev}^{-1}(b_0, y_1, \ldots , y_n)$
, where
![]() $y_1, \ldots , y_n$
are general points in
$y_1, \ldots , y_n$
are general points in
![]() $\mathbb {P}^r$
considered up to projective equivalence. We will show in Lemma 3.2 that every point
$\mathbb {P}^r$
considered up to projective equivalence. We will show in Lemma 3.2 that every point
![]() $[C_0, \ell ]\in \mathrm {ev}^{-1}(b_0, y_1, \ldots , y_n)$
corresponds to a limit linear series
$[C_0, \ell ]\in \mathrm {ev}^{-1}(b_0, y_1, \ldots , y_n)$
corresponds to a limit linear series
![]() $\ell \in \overline {G}^r_d(C_0)$
which is base point free at each point
$\ell \in \overline {G}^r_d(C_0)$
which is base point free at each point
![]() $x_1, \ldots , x_n$
. In particular,
$x_1, \ldots , x_n$
. In particular,
![]() $\mathrm {ev}^{-1}(b_0, y_1, \ldots , y_n)$
is disjoint from the indeterminacy locus of the map
$\mathrm {ev}^{-1}(b_0, y_1, \ldots , y_n)$
is disjoint from the indeterminacy locus of the map
![]() $\mathrm {ev}$
defined in (4).
$\mathrm {ev}$
defined in (4).
To that end, we wish to count limit linear series
![]() $\ell $
on
$\ell $
on
![]() $C_0$
of degree d and rank r, subject to the condition that, after twisting down base points on the
$C_0$
of degree d and rank r, subject to the condition that, after twisting down base points on the
![]() $R_0$
-aspect, the points
$R_0$
-aspect, the points
![]() $x_1,\ldots ,x_n$
have prescribed images in
$x_1,\ldots ,x_n$
have prescribed images in
![]() $\mathbb {P}^r$
. For a limit linear series
$\mathbb {P}^r$
. For a limit linear series
![]() $\ell $
on
$\ell $
on
![]() $C_0$
, we denote by
$C_0$
, we denote by
![]() $\ell _{R_0}, \ell _{R_{\operatorname {\mathrm {sp}}}}$
and
$\ell _{R_0}, \ell _{R_{\operatorname {\mathrm {sp}}}}$
and
![]() $\ell _{E_i}$
its corresponding aspects. By the additivity of the Brill-Noether number for
$\ell _{E_i}$
its corresponding aspects. By the additivity of the Brill-Noether number for
![]() $\ell $
encoded in the very definition of a limit linear series, we have the following inequality:
$\ell $
encoded in the very definition of a limit linear series, we have the following inequality:
 $$ \begin{align*}&\rho(g,r,d)\geq \rho\Bigl(\ell_{R_0}, \alpha^{\ell_{R_0}}(x_0)\Bigr) + \rho\Bigl(\ell_{R_{\mathrm{sp}}}, \alpha^{\ell_{R_{\operatorname{\mathrm{sp}}}}}(x_0), \alpha^{\ell_{R_{\mathrm{sp}}}}(p_1),\ldots, \alpha^{\ell_{R_{\operatorname{\mathrm{sp}}}}}(p_g)\Bigr)\\&\quad+ \sum_{i=1}^g \rho\Bigl(\ell_{E_i}, \alpha^{\ell_{E_i}}(p_i)\Bigr). \end{align*} $$
$$ \begin{align*}&\rho(g,r,d)\geq \rho\Bigl(\ell_{R_0}, \alpha^{\ell_{R_0}}(x_0)\Bigr) + \rho\Bigl(\ell_{R_{\mathrm{sp}}}, \alpha^{\ell_{R_{\operatorname{\mathrm{sp}}}}}(x_0), \alpha^{\ell_{R_{\mathrm{sp}}}}(p_1),\ldots, \alpha^{\ell_{R_{\operatorname{\mathrm{sp}}}}}(p_g)\Bigr)\\&\quad+ \sum_{i=1}^g \rho\Bigl(\ell_{E_i}, \alpha^{\ell_{E_i}}(p_i)\Bigr). \end{align*} $$
Since over the curve
![]() $[C_0, x_1, \ldots , x_n]$
the map
$[C_0, x_1, \ldots , x_n]$
the map
![]() $\mathrm {ev}$
evaluates the
$\mathrm {ev}$
evaluates the
![]() $R_0$
-aspect of each limit linear series, it follows that we must only consider the components of
$R_0$
-aspect of each limit linear series, it follows that we must only consider the components of
![]() $\overline {G}^r_d(C_0)$
in which
$\overline {G}^r_d(C_0)$
in which
![]() $\ell _{R_0}$
varies in a family of dimension
$\ell _{R_0}$
varies in a family of dimension
![]() $\rho (g,r, d)=\dim P_r^n$
. This happens when the remaining aspects of
$\rho (g,r, d)=\dim P_r^n$
. This happens when the remaining aspects of
![]() $\ell $
satisfy
$\ell $
satisfy
![]() $\rho \bigl (\ell _{E_i}, \alpha ^{\ell _{E_i}}(p_i)\bigr )=0$
for
$\rho \bigl (\ell _{E_i}, \alpha ^{\ell _{E_i}}(p_i)\bigr )=0$
for
![]() $i=1, \ldots , g$
and
$i=1, \ldots , g$
and
![]() $\rho \Bigl (\ell _{R_{\operatorname {\mathrm {sp}}}}, \alpha ^{\ell _{R_{\operatorname {\mathrm {sp}}}}}(x_0), \alpha ^{\ell _{R_{\operatorname {\mathrm {sp}}}}}(p_1),\ldots , \alpha ^{\ell _{R_{\mathrm {sp}}}}(p_g)\Bigr )=0$
.
$\rho \Bigl (\ell _{R_{\operatorname {\mathrm {sp}}}}, \alpha ^{\ell _{R_{\operatorname {\mathrm {sp}}}}}(x_0), \alpha ^{\ell _{R_{\operatorname {\mathrm {sp}}}}}(p_1),\ldots , \alpha ^{\ell _{R_{\mathrm {sp}}}}(p_g)\Bigr )=0$
.
This implies that on each elliptic tail
![]() $E_i$
, the ramification sequence at the node
$E_i$
, the ramification sequence at the node
![]() $p_i$
must be equal to
$p_i$
must be equal to
![]() $(d-r-1, \ldots , d-r-1,d-r)$
. Indeed, we need
$(d-r-1, \ldots , d-r-1,d-r)$
. Indeed, we need
![]() $\alpha ^{\ell _{E_i}}_r(p_i)=d-r$
, or else:
$\alpha ^{\ell _{E_i}}_r(p_i)=d-r$
, or else:
but also
![]() $\alpha ^{\ell _{E_i}}_{r-1}(p_i)\le d-r-1$
, or else
$\alpha ^{\ell _{E_i}}_{r-1}(p_i)\le d-r-1$
, or else
![]() $E_i$
would carry a linear series of rank 1 and degree 1. We therefore have a unique choice of the
$E_i$
would carry a linear series of rank 1 and degree 1. We therefore have a unique choice of the
![]() $E_i$
-aspect, precisely
$E_i$
-aspect, precisely
![]() $\ell _{E_i}=(d-r-1)p_i+\bigl |(r+1)p_i\bigr |$
, for
$\ell _{E_i}=(d-r-1)p_i+\bigl |(r+1)p_i\bigr |$
, for
![]() $i=1, \ldots , g$
. By compatibility of the aspects of limit linear series, we find that
$i=1, \ldots , g$
. By compatibility of the aspects of limit linear series, we find that
![]() $\alpha ^{\ell _{R_{\operatorname {\mathrm {sp}}}}}(p_i)=(0, 1, \ldots , 1)$
for
$\alpha ^{\ell _{R_{\operatorname {\mathrm {sp}}}}}(p_i)=(0, 1, \ldots , 1)$
for
![]() $i=1, \ldots , g$
, that is,
$i=1, \ldots , g$
, that is,
![]() $\ell _{R_{\operatorname {\mathrm {sp}}}}$
has a simple cusp at each of the points
$\ell _{R_{\operatorname {\mathrm {sp}}}}$
has a simple cusp at each of the points
![]() $p_i, \ldots , p_g$
.
$p_i, \ldots , p_g$
.
From here, on
![]() $R_{\operatorname {\mathrm {sp}}}$
, the ramification sequence of
$R_{\operatorname {\mathrm {sp}}}$
, the ramification sequence of
![]() $\ell $
at the point
$\ell $
at the point
![]() $x_0$
:
$x_0$
:
must satisfy the equality:
 $$ \begin{align*} \sum_{j=0}^{r}\alpha^{\ell_{R_{\operatorname{\mathrm{sp}}}}}_{j}(x_0)=(r+1)(d-r)-rg, \end{align*} $$
$$ \begin{align*} \sum_{j=0}^{r}\alpha^{\ell_{R_{\operatorname{\mathrm{sp}}}}}_{j}(x_0)=(r+1)(d-r)-rg, \end{align*} $$
whereas the
![]() $R_0$
-aspect of
$R_0$
-aspect of
![]() $\ell $
satisfies:
$\ell $
satisfies:
 $$ \begin{align} \sum_{j=0}^r \alpha_j^{\ell_{R_0}}(x_0)=rg. \end{align} $$
$$ \begin{align} \sum_{j=0}^r \alpha_j^{\ell_{R_0}}(x_0)=rg. \end{align} $$
Let
![]() $\mu =(\mu _0\geq \cdots \geq \mu _r):=\overline {\alpha ^{\ell _{R_{\operatorname {\mathrm {sp}}}}}_{r}(x_0)}$
, that is, we write the partition
$\mu =(\mu _0\geq \cdots \geq \mu _r):=\overline {\alpha ^{\ell _{R_{\operatorname {\mathrm {sp}}}}}_{r}(x_0)}$
, that is, we write the partition
![]() $\Big(\alpha ^{\ell _{R_{\operatorname {\mathrm {sp}}}}}_{r}(x_0),\ldots ,\alpha ^{\ell _{R_{\operatorname {\mathrm {sp}}}}}_{0}(x_0)\Big )$
, where the ramification indices are given in descending order, and let
$\Big(\alpha ^{\ell _{R_{\operatorname {\mathrm {sp}}}}}_{r}(x_0),\ldots ,\alpha ^{\ell _{R_{\operatorname {\mathrm {sp}}}}}_{0}(x_0)\Big )$
, where the ramification indices are given in descending order, and let
![]() $\lambda $
be the complement of
$\lambda $
be the complement of
![]() $\mu $
in
$\mu $
in
![]() $(d-r)^{r+1}$
, that is,
$(d-r)^{r+1}$
, that is,
![]() $\lambda _j=d-r-\mu _j$
, for
$\lambda _j=d-r-\mu _j$
, for
![]() $j=0,1,\ldots ,r$
. Summarising the discussion so far, for each limit linear series
$j=0,1,\ldots ,r$
. Summarising the discussion so far, for each limit linear series
![]() $\ell $
on
$\ell $
on
![]() $C_0$
contributing towards the degree of the map
$C_0$
contributing towards the degree of the map
![]() $\mathrm {ev}$
, one has:
$\mathrm {ev}$
, one has:
The number of possible aspects
![]() $\ell _{R_{\operatorname {\mathrm {sp}}}}$
on
$\ell _{R_{\operatorname {\mathrm {sp}}}}$
on
![]() $R_{\operatorname {\mathrm {sp}}}$
with ramification sequence
$R_{\operatorname {\mathrm {sp}}}$
with ramification sequence
![]() $\overline {\mu }$
at
$\overline {\mu }$
at
![]() $x_0$
and cusps at
$x_0$
and cusps at
![]() $p_1, \ldots , p_g$
is given by:
$p_1, \ldots , p_g$
is given by:
 $$ \begin{align*} \beta_{\lambda}:=\int_{\operatorname{\mathrm{Gr}}(r+1,d+1)}\sigma_{1^r}^g\cdot \sigma_{\mu}. \end{align*} $$
$$ \begin{align*} \beta_{\lambda}:=\int_{\operatorname{\mathrm{Gr}}(r+1,d+1)}\sigma_{1^r}^g\cdot \sigma_{\mu}. \end{align*} $$
The transversality of the intersection follows from [Reference Eisenbud and Harris6], see also [Reference Mukhin, Tarasov and Varchenko15], that is, for a general choice of the points
![]() $p_1, \ldots , p_g$
and
$p_1, \ldots , p_g$
and
![]() $x_0$
, one has precisely
$x_0$
, one has precisely
![]() $\beta _{\lambda }$
distinct linear series on
$\beta _{\lambda }$
distinct linear series on
![]() $R_{\operatorname {\mathrm {sp}}}$
with these property. Since
$R_{\operatorname {\mathrm {sp}}}$
with these property. Since
![]() $\sigma _{\lambda '}\cdot \sigma _{\mu }=0$
, for any Schubert index
$\sigma _{\lambda '}\cdot \sigma _{\mu }=0$
, for any Schubert index
![]() $\lambda '\neq \lambda $
with
$\lambda '\neq \lambda $
with
![]() $|\lambda '|=rg$
, whereas
$|\lambda '|=rg$
, whereas
![]() $\sigma _{\lambda }\cdot \sigma _{\mu }=1$
, we can write:
$\sigma _{\lambda }\cdot \sigma _{\mu }=1$
, we can write:
 $$ \begin{align} \sigma_{1^r}^g=\sum_{|\lambda|=rg}\beta_{\lambda}\cdot \sigma_{\lambda}\in \operatorname{{\mathrm{CH}}}^{g}\bigl(\operatorname{\mathrm{Gr}}(r+1,d+1)\bigr). \end{align} $$
$$ \begin{align} \sigma_{1^r}^g=\sum_{|\lambda|=rg}\beta_{\lambda}\cdot \sigma_{\lambda}\in \operatorname{{\mathrm{CH}}}^{g}\bigl(\operatorname{\mathrm{Gr}}(r+1,d+1)\bigr). \end{align} $$
Definition 2.2. Given a partition
![]() $\lambda =\bigl (\lambda _0\geq \cdots \geq \lambda _r\bigr )$
with
$\lambda =\bigl (\lambda _0\geq \cdots \geq \lambda _r\bigr )$
with
![]() $|\lambda |=rg$
and general points
$|\lambda |=rg$
and general points
![]() $y_1, \ldots , y_n\in \mathbb {P}^r$
, we define
$y_1, \ldots , y_n\in \mathbb {P}^r$
, we define
![]() $L_{g,r,d,\lambda }$
to be the number of maps
$L_{g,r,d,\lambda }$
to be the number of maps
![]() $f\colon \mathbb {P}^1\to \mathbb {P}^r$
of degree
$f\colon \mathbb {P}^1\to \mathbb {P}^r$
of degree
![]() $d-\lambda _r$
sending
$d-\lambda _r$
sending
![]() $x_i$
to
$x_i$
to
![]() $y_i$
for
$y_i$
for
![]() $i=1, \ldots , n$
and with ramification sequence given by
$i=1, \ldots , n$
and with ramification sequence given by
![]() $\overline {\lambda }$
at
$\overline {\lambda }$
at
![]() $x_0$
.
$x_0$
.
Such maps are obtained by twisting the
![]() $R_0$
-aspect of each limit linear series
$R_0$
-aspect of each limit linear series
![]() $\ell $
on
$\ell $
on
![]() $C_0$
by the order
$C_0$
by the order
![]() $\lambda _r$
of its base point
$\lambda _r$
of its base point
![]() $x_0$
. Our degeneration shows:
$x_0$
. Our degeneration shows:
Proposition 2.3. For a general n-pointed curve
![]() $[C,x_1, \ldots , x_n]$
of genus g, the degree of the map
$[C,x_1, \ldots , x_n]$
of genus g, the degree of the map
![]() $\mathrm {ev}_{(x_1, \ldots , x_n)}$
is given by the formula:
$\mathrm {ev}_{(x_1, \ldots , x_n)}$
is given by the formula:
 $$ \begin{align*} L_{g,r,d}=\sum_{|\lambda|=rg}\beta_{\lambda}L_{g,r,d,\lambda}. \end{align*} $$
$$ \begin{align*} L_{g,r,d}=\sum_{|\lambda|=rg}\beta_{\lambda}L_{g,r,d,\lambda}. \end{align*} $$
Proof. We have already explained that
![]() $L_{g,r,d}$
is the degree of the map
$L_{g,r,d}$
is the degree of the map
![]() $\mbox {ev}\colon \widetilde {\mathcal {G}}^r_d/B\dashrightarrow B\times P_r^n$
. Having fixed general points
$\mbox {ev}\colon \widetilde {\mathcal {G}}^r_d/B\dashrightarrow B\times P_r^n$
. Having fixed general points
![]() $y_1, \ldots , y_n\in \mathbb P^r$
, the fibre over
$y_1, \ldots , y_n\in \mathbb P^r$
, the fibre over
![]() $(b_0, y_1, \ldots , y_n)\in B\times P_r^n$
of the map
$(b_0, y_1, \ldots , y_n)\in B\times P_r^n$
of the map
![]() $\mathrm {ev}$
is then scheme-theoretically isomorphic to the variety of limit linear series
$\mathrm {ev}$
is then scheme-theoretically isomorphic to the variety of limit linear series
![]() $\ell \in \overline {G}^r_d(C_0)$
, whose
$\ell \in \overline {G}^r_d(C_0)$
, whose
![]() $R_0$
-aspect maps the marked points
$R_0$
-aspect maps the marked points
![]() $x_i$
to
$x_i$
to
![]() $y_i$
for
$y_i$
for
![]() $i=1, \ldots , n$
. From the discussion above, it follows that
$i=1, \ldots , n$
. From the discussion above, it follows that
![]() $\overline {G}^r_d\bigl (C_0\bigr )$
contains
$\overline {G}^r_d\bigl (C_0\bigr )$
contains
![]() $\beta _{\lambda }$
components all isomorphic to the variety
$\beta _{\lambda }$
components all isomorphic to the variety
![]() $G^r_d\bigl (R_0, (x_0, \overline {\lambda })\bigr )$
; the remaining components of
$G^r_d\bigl (R_0, (x_0, \overline {\lambda })\bigr )$
; the remaining components of
![]() $\overline {G}^r_d(C_0)$
do not contribute to the degree of
$\overline {G}^r_d(C_0)$
do not contribute to the degree of
![]() $\mathrm {ev}$
. Finally, observe that
$\mathrm {ev}$
. Finally, observe that
![]() $L_{g,r,d,\lambda }$
is precisely the contribution to the degree of the map
$L_{g,r,d,\lambda }$
is precisely the contribution to the degree of the map
![]() $\mathrm {ev}$
corresponding to the component
$\mathrm {ev}$
corresponding to the component
![]() $G^r_d\bigl (R_0, (x_0, \overline {\lambda })\bigr )$
.
$G^r_d\bigl (R_0, (x_0, \overline {\lambda })\bigr )$
.
3 Counting linear series with assigned incidences on
 $\mathbb {P}^1$
$\mathbb {P}^1$
Having reduced both Theorems 1.1 and 1.2 to a question on rational curves, we use Schubert calculus to complete their proofs.
Let us first sketch the argument. The set of maps
![]() $\mathbb {P}^1\to \mathbb {P}^r$
counted by the number
$\mathbb {P}^1\to \mathbb {P}^r$
counted by the number
![]() $L_{g,r,d,\lambda }$
naturally sits inside the projective space
$L_{g,r,d,\lambda }$
naturally sits inside the projective space
![]() $\mathbb {P}^{(r+1)(d+1)-1}$
parametrising morphisms
$\mathbb {P}^{(r+1)(d+1)-1}$
parametrising morphisms
![]() $f=[f_0, \ldots , f_r]$
of degree d, as given by the intersection of the conditions:
$f=[f_0, \ldots , f_r]$
of degree d, as given by the intersection of the conditions:
-
(i)
 $f(x_i)=y_i$
for
$f(x_i)=y_i$
for
 $i=1, \ldots ,n$
,
$i=1, \ldots ,n$
, -
(ii) f has ramification at least
 $\overline {\lambda }$
at
$\overline {\lambda }$
at
 $x_0$
.
$x_0$
.
The conditions
![]() $f(x_i)=y_i$
cut out linear subspaces, while, upon summing over all
$f(x_i)=y_i$
cut out linear subspaces, while, upon summing over all
![]() $\lambda $
with the multiplicities
$\lambda $
with the multiplicities
![]() $\beta _\lambda $
, the ramification conditions at
$\beta _\lambda $
, the ramification conditions at
![]() $x_0$
cut out an intersection of g subvarieties of degree
$x_0$
cut out an intersection of g subvarieties of degree
![]() $r+1$
. The expected degree of the intersection is therefore
$r+1$
. The expected degree of the intersection is therefore
![]() $(r+1)^g$
, and we show in the proof of Theorem 1.1 that this intersection is indeed transverse when
$(r+1)^g$
, and we show in the proof of Theorem 1.1 that this intersection is indeed transverse when
![]() $d\ge rg+r$
.
$d\ge rg+r$
.
In general, however, the intersection described above has many excess components. Under the conditions of Theorem 1.2, we remove these excess contributions by passing to a certain incidence correspondence dominating
![]() $\mathbb {P}^{(r+1)(d+1)-1}$
to compute
$\mathbb {P}^{(r+1)(d+1)-1}$
to compute
![]() $L_{g,r,d}$
.
$L_{g,r,d}$
.
3.1 Proof of Theorem 1.1
For a complex polynomial
![]() $u=a_0+\cdots +a_dt^d$
, we denote by
$u=a_0+\cdots +a_dt^d$
, we denote by
![]() $c(u)$
the column vector of its coefficients. Let
$c(u)$
the column vector of its coefficients. Let
![]() $\mathbb {P}^{(r+1)(d+1)-1}$
be the projective space parametrising
$\mathbb {P}^{(r+1)(d+1)-1}$
be the projective space parametrising
![]() $(r+1)$
-tuples
$(r+1)$
-tuples
![]() $(f_0,\ldots ,f_r)$
of polynomials of degree d in one variable viewed as sections of
$(f_0,\ldots ,f_r)$
of polynomials of degree d in one variable viewed as sections of
![]() $\mathcal {O}_{\mathbb {P}^1}(d)$
, up to simultaneous scaling, and not all zero. When not all polynomials
$\mathcal {O}_{\mathbb {P}^1}(d)$
, up to simultaneous scaling, and not all zero. When not all polynomials
![]() $f_i$
are zero and have no common zeroes, they define a map
$f_i$
are zero and have no common zeroes, they define a map
![]() $f=[f_0, \ldots , f_r]$
of degree d from
$f=[f_0, \ldots , f_r]$
of degree d from
![]() $\mathbb {P}^1$
to
$\mathbb {P}^1$
to
![]() $\mathbb {P}^r$
.
$\mathbb {P}^r$
.
We introduce the map:
remembering the linear series spanned by
![]() $f_0, \ldots , f_r$
, whenever they are linearly independent. The indeterminacy locus of this map is irreducible of codimension
$f_0, \ldots , f_r$
, whenever they are linearly independent. The indeterminacy locus of this map is irreducible of codimension
![]() $d-r+1$
, for an
$d-r+1$
, for an
![]() $(r+1)$
-tuple of polynomials
$(r+1)$
-tuple of polynomials
![]() $(f_0, \ldots , f_r)$
lies in the indeterminacy locus of
$(f_0, \ldots , f_r)$
lies in the indeterminacy locus of
![]() $\pi $
if and only if the
$\pi $
if and only if the
![]() $(r+1)\times (d+1)$
-matrix of coefficients
$(r+1)\times (d+1)$
-matrix of coefficients
![]() $\bigl (c(f_0), \ldots , c(f_r)\bigr )$
has rank at most r.
$\bigl (c(f_0), \ldots , c(f_r)\bigr )$
has rank at most r.
For a Schubert variety
![]() $\Sigma _\lambda =\Sigma _{\lambda }({\textbf F})\subseteq \operatorname {\mathrm {Gr}}(r+1,d+1)$
of codimension at most
$\Sigma _\lambda =\Sigma _{\lambda }({\textbf F})\subseteq \operatorname {\mathrm {Gr}}(r+1,d+1)$
of codimension at most
![]() $rg$
in
$rg$
in
![]() $\operatorname {\mathrm {Gr}}(r+1,d+1)$
, let
$\operatorname {\mathrm {Gr}}(r+1,d+1)$
, let
![]() $\widetilde {\Sigma }_{\lambda }:=(\pi _1)_*\bigl (\pi _2^*(\Sigma _{\lambda })\bigr )$
be the closure of its pullback under
$\widetilde {\Sigma }_{\lambda }:=(\pi _1)_*\bigl (\pi _2^*(\Sigma _{\lambda })\bigr )$
be the closure of its pullback under
![]() $\mathbb {P}^{(r+1)(d+1)-1}$
. Because the codimension of
$\mathbb {P}^{(r+1)(d+1)-1}$
. Because the codimension of
![]() $\Sigma _{\lambda }$
is lower than that of the indeterminacy locus of
$\Sigma _{\lambda }$
is lower than that of the indeterminacy locus of
![]() $\pi $
(by our assumption,
$\pi $
(by our assumption,
![]() $d-r+1>rg$
), the cycle
$d-r+1>rg$
), the cycle
![]() $\widetilde {\Sigma }_{\lambda }$
has the expected codimension of
$\widetilde {\Sigma }_{\lambda }$
has the expected codimension of
![]() $|\lambda |=rg$
and defines a well-defined class
$|\lambda |=rg$
and defines a well-defined class
![]() $\widetilde {\sigma }_{\lambda }\in \operatorname {{\mathrm {CH}}}^{rg}\bigl (\mathbb {P}^{(r+1)(d+1)-1}\bigr )$
. Using (7) we have the formula:
$\widetilde {\sigma }_{\lambda }\in \operatorname {{\mathrm {CH}}}^{rg}\bigl (\mathbb {P}^{(r+1)(d+1)-1}\bigr )$
. Using (7) we have the formula:
 $$ \begin{align*} \widetilde{\sigma}_{1^r}^{g}=\sum_{|\lambda|=rg}\beta_{\lambda}\widetilde{\sigma}_{\lambda}. \end{align*} $$
$$ \begin{align*} \widetilde{\sigma}_{1^r}^{g}=\sum_{|\lambda|=rg}\beta_{\lambda}\widetilde{\sigma}_{\lambda}. \end{align*} $$
Recall that we have fixed n general points
![]() $y_1, \ldots , y_n\in \mathbb {P}^r$
. The condition on maps
$y_1, \ldots , y_n\in \mathbb {P}^r$
. The condition on maps
![]() $f\colon \mathbb {P}^1\to \mathbb {P}^r$
that
$f\colon \mathbb {P}^1\to \mathbb {P}^r$
that
![]() $f(x_i)=y_i$
for
$f(x_i)=y_i$
for
![]() $i=1, \ldots , n$
impose
$i=1, \ldots , n$
impose
![]() $nr$
linear conditions on the matrix of coefficients
$nr$
linear conditions on the matrix of coefficients
![]() $\bigl (c(f_0), \ldots , c(f_r)\bigr )$
. Observe that this condition is automatically satisfied for those i for which
$\bigl (c(f_0), \ldots , c(f_r)\bigr )$
. Observe that this condition is automatically satisfied for those i for which
![]() $x_i$
is a base point of f. The points
$x_i$
is a base point of f. The points
![]() $y_1, \ldots , y_n$
having been chosen to be general, these linear conditions are independent. Since
$y_1, \ldots , y_n$
having been chosen to be general, these linear conditions are independent. Since
![]() $(r+1)(d+1)-1-nr=rg$
, the conditions
$(r+1)(d+1)-1-nr=rg$
, the conditions
![]() $f(x_i)=y_i$
give rise to a linear subspace:
$f(x_i)=y_i$
give rise to a linear subspace:
Now, let
![]() ${\Sigma }_{\lambda }(x_0)=G^r_d\bigl (\mathbb {P}^1, (x_0, \overline {\lambda }\bigr ))$
be the Schubert variety of
${\Sigma }_{\lambda }(x_0)=G^r_d\bigl (\mathbb {P}^1, (x_0, \overline {\lambda }\bigr ))$
be the Schubert variety of
![]() $\operatorname {\mathrm {Gr}}(r+1,d+1)$
parametrising linear series on
$\operatorname {\mathrm {Gr}}(r+1,d+1)$
parametrising linear series on
![]() $\mathbb {P}^1$
with ramification sequence at least
$\mathbb {P}^1$
with ramification sequence at least
![]() $\overline {\lambda }$
at
$\overline {\lambda }$
at
![]() $x_0$
. We wish to intersect its pullback
$x_0$
. We wish to intersect its pullback
![]() $\widetilde {\Sigma }_{\lambda }(x_0)$
with
$\widetilde {\Sigma }_{\lambda }(x_0)$
with
![]() ${\textbf L}$
on
${\textbf L}$
on
![]() $\mathbb {P}^{(r+1)(d+1)-1}$
. We call a point
$\mathbb {P}^{(r+1)(d+1)-1}$
. We call a point
![]() $[f_0,\ldots ,f_r]$
in this intersection generic if
$[f_0,\ldots ,f_r]$
in this intersection generic if
![]() $\langle f_0,\ldots ,f_r\rangle $
is a linear series of rank r with ramification sequence exactly
$\langle f_0,\ldots ,f_r\rangle $
is a linear series of rank r with ramification sequence exactly
![]() $\overline {\lambda }$
, and which defines a (nondegenerate) morphism
$\overline {\lambda }$
, and which defines a (nondegenerate) morphism
![]() $f\colon \mathbb {P}^1\to \mathbb {P}^r$
after twisting down the base points at
$f\colon \mathbb {P}^1\to \mathbb {P}^r$
after twisting down the base points at
![]() $x_0$
with
$x_0$
with
![]() $f(x_i)=y_i$
(in particular,
$f(x_i)=y_i$
(in particular,
![]() $\langle f_0,\ldots ,f_r\rangle $
has no base points away from
$\langle f_0,\ldots ,f_r\rangle $
has no base points away from
![]() $x_0$
).
$x_0$
).
Remark 3.1. We have already seen above that the condition
![]() $d\ge rg+r$
ensures that the classes
$d\ge rg+r$
ensures that the classes
![]() $\widetilde {\sigma }_{1^r}^g$
and
$\widetilde {\sigma }_{1^r}^g$
and
![]() $\widetilde {\sigma }_{\lambda }$
live in codimension strictly smaller than that of the indeterminacy locus of
$\widetilde {\sigma }_{\lambda }$
live in codimension strictly smaller than that of the indeterminacy locus of
![]() $\pi $
. However, as we will see in Lemma 3.2, the same condition
$\pi $
. However, as we will see in Lemma 3.2, the same condition
![]() $d\geq rg+r$
also ensures that
$d\geq rg+r$
also ensures that
![]() ${\textbf L}$
contains no points corresponding to degenerate maps
${\textbf L}$
contains no points corresponding to degenerate maps
![]() $f\colon \mathbb {P}^1\to \mathbb {P}^r$
. In fact, this is already evident in the case of constant maps; indeed, suppose instead that
$f\colon \mathbb {P}^1\to \mathbb {P}^r$
. In fact, this is already evident in the case of constant maps; indeed, suppose instead that
![]() $d\ge n-1$
. Then, we may take the nonzero polynomials
$d\ge n-1$
. Then, we may take the nonzero polynomials
![]() $f_0,\ldots ,f_r$
to vanish at
$f_0,\ldots ,f_r$
to vanish at
![]() $x_1,\ldots , x_{n-1}$
, and after twisting away all base points, the resulting map
$x_1,\ldots , x_{n-1}$
, and after twisting away all base points, the resulting map
![]() $f\colon \mathbb {P}^1\to \mathbb {P}^r$
to be the constant map with image
$f\colon \mathbb {P}^1\to \mathbb {P}^r$
to be the constant map with image
![]() $y_n$
. Then,
$y_n$
. Then,
![]() $f=[f_0,\ldots , f_r]$
lies on the one hand in
$f=[f_0,\ldots , f_r]$
lies on the one hand in
![]() ${\textbf L}$
, and on the other hand in the indeterminacy locus of
${\textbf L}$
, and on the other hand in the indeterminacy locus of
![]() $\pi $
.
$\pi $
.
Lemma 3.2. The intersection points of
![]() $\widetilde {\Sigma }_{\lambda }(x_0)$
with
$\widetilde {\Sigma }_{\lambda }(x_0)$
with
![]() ${\textbf L}$
are generic in the previous sense. In particular, the intersection occurs away from the indeterminacy locus of
${\textbf L}$
are generic in the previous sense. In particular, the intersection occurs away from the indeterminacy locus of
![]() $\pi $
.
$\pi $
.
Proof. We construct the locus
![]() ${\textbf L}$
‘relatively’, allowing the points
${\textbf L}$
‘relatively’, allowing the points
![]() $y_1,\ldots ,y_n$
to vary, and show that, for dimension reasons, the locus where
$y_1,\ldots ,y_n$
to vary, and show that, for dimension reasons, the locus where
![]() ${\textbf L}\cap \widetilde {\Sigma }_{\lambda }(x_0)$
contains nongeneric points cannot dominate the space of choices of the
${\textbf L}\cap \widetilde {\Sigma }_{\lambda }(x_0)$
contains nongeneric points cannot dominate the space of choices of the
![]() $y_i$
. In particular, if the
$y_i$
. In particular, if the
![]() $y_i$
are chosen to be general, we obtain the desired conclusion.
$y_i$
are chosen to be general, we obtain the desired conclusion.
More precisely, let
![]() $V\subseteq (\mathbb {P}^r)^n$
be the open subset of collections of points
$V\subseteq (\mathbb {P}^r)^n$
be the open subset of collections of points
![]() $y_1,\ldots ,y_n\in \mathbb {P}^r$
, where the
$y_1,\ldots ,y_n\in \mathbb {P}^r$
, where the
![]() $y_i$
are in linearly general position, that is, no m of the
$y_i$
are in linearly general position, that is, no m of the
![]() $y_i$
lie on a linear space of dimension
$y_i$
lie on a linear space of dimension
![]() $m-2$
if
$m-2$
if
![]() $2\le m\le r+1$
. Consider the product
$2\le m\le r+1$
. Consider the product
![]() $V\times \mathbb {P}^{(r+1)(d+1)-1}$
, where the second factor parametrises maps
$V\times \mathbb {P}^{(r+1)(d+1)-1}$
, where the second factor parametrises maps
![]() $f=[f_0,\ldots , f_r]$
as before, and the closed subscheme
$f=[f_0,\ldots , f_r]$
as before, and the closed subscheme
![]() $V\times \widetilde {\Sigma }_{\lambda }(x_0)$
of the expected dimension
$V\times \widetilde {\Sigma }_{\lambda }(x_0)$
of the expected dimension
![]() $rg$
as defined above. We then define the locus, abusively denoted
$rg$
as defined above. We then define the locus, abusively denoted
![]() ${\textbf L}\subseteq V\times \mathbb {P}^{(r+1)(d+1)-1}$
, of maps f satisfying
${\textbf L}\subseteq V\times \mathbb {P}^{(r+1)(d+1)-1}$
, of maps f satisfying
![]() $f(x_i)=y_i$
for
$f(x_i)=y_i$
for
![]() $i=1,2,\ldots ,n$
, by relativising the above construction.
$i=1,2,\ldots ,n$
, by relativising the above construction.
We have a forgetful map
![]() $\psi \colon {\textbf L}\cap \widetilde {\Sigma }_{\lambda }(x_0) \to V$
, and wish to show that the locus of nongeneric points of source does not dominate V; to do so, we show that the locus of nongeneric points has dimension strictly less than that of V.
$\psi \colon {\textbf L}\cap \widetilde {\Sigma }_{\lambda }(x_0) \to V$
, and wish to show that the locus of nongeneric points of source does not dominate V; to do so, we show that the locus of nongeneric points has dimension strictly less than that of V.
First, consider the locus on
![]() ${\textbf L}\cap \widetilde {\Sigma }_{\lambda }(x_0)$
of nongeneric
${\textbf L}\cap \widetilde {\Sigma }_{\lambda }(x_0)$
of nongeneric
![]() $f=[f_0, \ldots , f_r]\in {\textbf L}\cap \widetilde {\Sigma }_{\lambda }(x_0)$
away from the indeterminacy locus of
$f=[f_0, \ldots , f_r]\in {\textbf L}\cap \widetilde {\Sigma }_{\lambda }(x_0)$
away from the indeterminacy locus of
![]() $\pi $
. Suppose that f has base points of total order k away from
$\pi $
. Suppose that f has base points of total order k away from
![]() $x_0,\ldots , x_n$
and order
$x_0,\ldots , x_n$
and order
![]() $k'$
on
$k'$
on
![]() $x_1,\ldots ,x_n$
, and that
$x_1,\ldots ,x_n$
, and that
![]() $k+k'>0$
. We see upon twisting down by these base points that the locus of such f has the expected codimension
$k+k'>0$
. We see upon twisting down by these base points that the locus of such f has the expected codimension
![]() $(r+1)(k+k')$
in
$(r+1)(k+k')$
in
![]() $\widetilde {\Sigma }_{\lambda }(x_0)$
, and the incidence conditions
$\widetilde {\Sigma }_{\lambda }(x_0)$
, and the incidence conditions
![]() $f(x_i)=y_i$
impose at least
$f(x_i)=y_i$
impose at least
![]() $(n-k')r$
additional conditions inside
$(n-k')r$
additional conditions inside
![]() $V\times \widetilde {\Sigma }_{\lambda }(x_0)$
. In total, we find that the locus of possible f has codimension strictly greater than
$V\times \widetilde {\Sigma }_{\lambda }(x_0)$
. In total, we find that the locus of possible f has codimension strictly greater than
![]() $rg+rn$
in
$rg+rn$
in
![]() $V\times \widetilde {\Sigma }_{\lambda }(x_0)$
, and therefore cannot dominate V. Similarly, a parameter count shows that f cannot have ramification sequence strictly more than
$V\times \widetilde {\Sigma }_{\lambda }(x_0)$
, and therefore cannot dominate V. Similarly, a parameter count shows that f cannot have ramification sequence strictly more than
![]() $\overline {\lambda }$
at
$\overline {\lambda }$
at
![]() $x_0$
.
$x_0$
.
Consider now a point of
![]() ${\textbf L}\cap \widetilde {\Sigma }_{\lambda }(x_0)$
, for which
${\textbf L}\cap \widetilde {\Sigma }_{\lambda }(x_0)$
, for which
![]() $\mbox {dim} \langle f_0, \ldots , f_r\rangle \leq r$
. We show again by counting parameters that no such f can exist. By twisting away base points at
$\mbox {dim} \langle f_0, \ldots , f_r\rangle \leq r$
. We show again by counting parameters that no such f can exist. By twisting away base points at
![]() $x_0$
(which decreases the number of moduli and the number of conditions by the same amount), we may assume that f is base point free at
$x_0$
(which decreases the number of moduli and the number of conditions by the same amount), we may assume that f is base point free at
![]() $x_0$
. We may also assume that f has no base points away from
$x_0$
. We may also assume that f has no base points away from
![]() $x_1,\ldots , x_n$
. Suppose now that f has k (simple) base points among these
$x_1,\ldots , x_n$
. Suppose now that f has k (simple) base points among these
![]() $x_i$
, we label them as
$x_i$
, we label them as
![]() $x_{n-k+1}, \ldots , x_n$
; we twist down our linear series to have degree
$x_{n-k+1}, \ldots , x_n$
; we twist down our linear series to have degree
![]() $d-k$
, and lose the corresponding k linear conditions. Note that in this case, the ramification condition at
$d-k$
, and lose the corresponding k linear conditions. Note that in this case, the ramification condition at
![]() $x_0$
can no longer be imposed in terms of
$x_0$
can no longer be imposed in terms of
![]() $f_0, \ldots , f_r$
alone, since by assumption, the resulting map
$f_0, \ldots , f_r$
alone, since by assumption, the resulting map
![]() $f\colon \mathbb {P}^1\to \mathbb {P}^r$
is degenerate, that is, the corresponding linear series has dimension
$f\colon \mathbb {P}^1\to \mathbb {P}^r$
is degenerate, that is, the corresponding linear series has dimension
![]() $r'<r$
. Note, however, that if the remaining
$r'<r$
. Note, however, that if the remaining
![]() $y_i$
do not themselves live in a linear subspace of
$y_i$
do not themselves live in a linear subspace of
![]() $\mathbb {P}^r$
of dimension
$\mathbb {P}^r$
of dimension
![]() $r'$
, then this is impossible; we therefore need
$r'$
, then this is impossible; we therefore need
![]() $n-k\le r'+1$
.
$n-k\le r'+1$
.
Then, it must be true that if
![]() $x_1,\ldots ,x_{n-k}$
are general points of
$x_1,\ldots ,x_{n-k}$
are general points of
![]() $\mathbb {P}^1$
, there exists a map
$\mathbb {P}^1$
, there exists a map
![]() $f\colon \mathbb {P}^1\to \mathbb {P}^{r'}$
of degree
$f\colon \mathbb {P}^1\to \mathbb {P}^{r'}$
of degree
![]() $d-k$
with
$d-k$
with
![]() $f(x_i)=y_i$
for
$f(x_i)=y_i$
for
![]() $i=1,\ldots , n-k$
. Therefore, we have:
$i=1,\ldots , n-k$
. Therefore, we have:
Rearranging yields:
On the other hand, because
![]() $n-k\le r'+1$
, we find:
$n-k\le r'+1$
, we find:
However, by assumption, we have
![]() $n\ge d+2$
and
$n\ge d+2$
and
![]() $r'\ge 0$
, so we have reached a contradiction.
$r'\ge 0$
, so we have reached a contradiction.
Lemma 3.3. For a general choice of the points
![]() $x_1, \ldots , x_n\in \mathbb {P}^1$
and
$x_1, \ldots , x_n\in \mathbb {P}^1$
and
![]() $y_1, \ldots , y_n\in \mathbb {P}^r$
, the intersection of
$y_1, \ldots , y_n\in \mathbb {P}^r$
, the intersection of
![]() $\widetilde {\Sigma }_{\lambda }(x_0)$
and
$\widetilde {\Sigma }_{\lambda }(x_0)$
and
![]() ${\textbf L}$
is transverse.
${\textbf L}$
is transverse.
Proof. Let
![]() $\mathcal {M}_{n,d,r}$
be the open subscheme of the space
$\mathcal {M}_{n,d,r}$
be the open subscheme of the space
![]() $\operatorname {\mathrm {Hom}}_d(\mathbb {P}^1,\mathbb {P}^r)\times (\mathbb {P}^1)^n$
parametrising elements
$\operatorname {\mathrm {Hom}}_d(\mathbb {P}^1,\mathbb {P}^r)\times (\mathbb {P}^1)^n$
parametrising elements
![]() $([f\colon \mathbb {P}^1\to \mathbb {P}^r],x_1,\ldots ,x_n)$
, where f is a nondegenerate morphism of degree d and the
$([f\colon \mathbb {P}^1\to \mathbb {P}^r],x_1,\ldots ,x_n)$
, where f is a nondegenerate morphism of degree d and the
![]() $x_i$
are pairwise distinct points that in addition are distinct from a fixed point
$x_i$
are pairwise distinct points that in addition are distinct from a fixed point
![]() $x_0\in \mathbb {P}^1$
.
$x_0\in \mathbb {P}^1$
.
One may construct
![]() $\mathcal {M}_{n,d,r}$
as an open subset of a
$\mathcal {M}_{n,d,r}$
as an open subset of a
![]() $(\mathbb {P}^1)^{n}$
-bundle over
$(\mathbb {P}^1)^{n}$
-bundle over
![]() $\mathbb {P}^{(r+1)(d+1)-1}$
. We have a smooth, regular map
$\mathbb {P}^{(r+1)(d+1)-1}$
. We have a smooth, regular map
![]() $\chi \colon \mathcal {M}_{n,d,r}\to \operatorname {\mathrm {Gr}}(r+1,d+1)$
, from which we can pull back the smooth, open Schubert cycle of linear series with ramification exactly
$\chi \colon \mathcal {M}_{n,d,r}\to \operatorname {\mathrm {Gr}}(r+1,d+1)$
, from which we can pull back the smooth, open Schubert cycle of linear series with ramification exactly
![]() $\overline {\lambda }$
at
$\overline {\lambda }$
at
![]() $x_0$
to obtain the smooth subscheme
$x_0$
to obtain the smooth subscheme
![]() $Y_{n,d,r}$
parametrising the morphisms we wish to count. Finally, the projection
$Y_{n,d,r}$
parametrising the morphisms we wish to count. Finally, the projection
![]() $\phi \colon Y_{n,d,r}\to (\mathbb {P}^1)^{n+1}\times (\mathbb {P}^r)^n$
remembering the marked points and their images on the source is generically unramified of finite degree.
$\phi \colon Y_{n,d,r}\to (\mathbb {P}^1)^{n+1}\times (\mathbb {P}^r)^n$
remembering the marked points and their images on the source is generically unramified of finite degree.
By construction, any nonzero tangent vector to the intersection
![]() $\widetilde {\Sigma }_{\lambda }(x_0)$
and
$\widetilde {\Sigma }_{\lambda }(x_0)$
and
![]() ${\textbf L}$
in the generic locus yields a nonzero relative tangent vector of
${\textbf L}$
in the generic locus yields a nonzero relative tangent vector of
![]() $\phi $
. Thus, when the points
$\phi $
. Thus, when the points
![]() $x_i, y_i$
are general, there are no such tangent vectors, and the intersection is transverse.
$x_i, y_i$
are general, there are no such tangent vectors, and the intersection is transverse.
We are now in a position to complete the proof of Theorem 1.1.
Proof of Theorem 1.1
By the above discussion summarised in Proposition 2.3, it suffices to intersect
![]() $nr$
linear conditions with
$nr$
linear conditions with
![]() $\widetilde {\sigma }_{1^r}^{g}$
on
$\widetilde {\sigma }_{1^r}^{g}$
on
![]() $\mathbb {P}^{(r+1)(d+1)-1}$
and compute the degree, that is:
$\mathbb {P}^{(r+1)(d+1)-1}$
and compute the degree, that is:
 $$ \begin{align*} L_{g,r,d}=\sum_{|\lambda|=rg} \beta_{\lambda} {\textbf L}\cdot \widetilde{\sigma}_{\lambda}={\textbf L}\cdot \widetilde{\sigma}_{1^r}^g=\mathrm{deg}\bigl(\widetilde{\sigma}_{1^r}^g\bigr)=\mathrm{deg}\bigl(\sigma_{1^r}^g\bigr), \end{align*} $$
$$ \begin{align*} L_{g,r,d}=\sum_{|\lambda|=rg} \beta_{\lambda} {\textbf L}\cdot \widetilde{\sigma}_{\lambda}={\textbf L}\cdot \widetilde{\sigma}_{1^r}^g=\mathrm{deg}\bigl(\widetilde{\sigma}_{1^r}^g\bigr)=\mathrm{deg}\bigl(\sigma_{1^r}^g\bigr), \end{align*} $$
where the last two degrees are computed on
![]() $\operatorname {\mathrm {Gr}}(r+1,d+1)$
and on
$\operatorname {\mathrm {Gr}}(r+1,d+1)$
and on
![]() $\mathbb {P}^{(r+1)(d+1)-1}$
, respectively.
$\mathbb {P}^{(r+1)(d+1)-1}$
, respectively.
Theorem 1.1 then follows from the fact that the degree of
![]() $\widetilde {\sigma }_{1^r}$
is
$\widetilde {\sigma }_{1^r}$
is
![]() $r+1$
. To see this, note that on
$r+1$
. To see this, note that on
![]() $\operatorname {\mathrm {Gr}}(r+1,d+1)$
, the Schubert cycle
$\operatorname {\mathrm {Gr}}(r+1,d+1)$
, the Schubert cycle
![]() $\Sigma _{1^r}$
is the locus of
$\Sigma _{1^r}$
is the locus of
![]() $(r+1)$
-planes intersecting a fixed codimension 2 subspace
$(r+1)$
-planes intersecting a fixed codimension 2 subspace
![]() $P\subseteq H^0(\mathbb {P}^1,\mathcal {O}(d))$
in a subspace of dimension at least r. Identifying
$P\subseteq H^0(\mathbb {P}^1,\mathcal {O}(d))$
in a subspace of dimension at least r. Identifying
![]() $\mathbb {P}^{(r+1)(d+1)-1}$
with the space of
$\mathbb {P}^{(r+1)(d+1)-1}$
with the space of
![]() $(r+1)\times (d+1)$
matrices, whose entries are taken up to simultaneous scaling, the pullback of
$(r+1)\times (d+1)$
matrices, whose entries are taken up to simultaneous scaling, the pullback of
![]() $\Sigma _{1^r}$
may be identified with the determinantal locus of matrices, such that the
$\Sigma _{1^r}$
may be identified with the determinantal locus of matrices, such that the
![]() $(r+1)\times 2$
submatrix formed by the first two columns has rank 1. This, in turn, is the pullback under linear projection from
$(r+1)\times 2$
submatrix formed by the first two columns has rank 1. This, in turn, is the pullback under linear projection from
![]() $\mathbb {P}^{(r+1)(d+1)-1}$
of the Segre embedding
$\mathbb {P}^{(r+1)(d+1)-1}$
of the Segre embedding
![]() $\mathbb {P}^{1}\times \mathbb {P}^{r}\to \mathbb {P}^{2r+1}$
. Denoting by
$\mathbb {P}^{1}\times \mathbb {P}^{r}\to \mathbb {P}^{2r+1}$
. Denoting by
![]() $h_1$
and
$h_1$
and
![]() $h_2$
the pullbacks to
$h_2$
the pullbacks to
![]() $\mathbb {P}^1\times \mathbb {P}^{r+1}$
of the hyperplane classes of
$\mathbb {P}^1\times \mathbb {P}^{r+1}$
of the hyperplane classes of
![]() $\mathbb {P}^1$
and
$\mathbb {P}^1$
and
![]() $\mathbb {P}^{r+1}$
, observe that:
$\mathbb {P}^{r+1}$
, observe that:
 $$ \begin{align*} \mbox{deg}\bigl(\mathbb{P}^1\times \mathbb{P}^{r}\bigr)=(h_1+h_2)^{r+1}={r+1\choose 1}h_1 h_2^r=r+1. \end{align*} $$
$$ \begin{align*} \mbox{deg}\bigl(\mathbb{P}^1\times \mathbb{P}^{r}\bigr)=(h_1+h_2)^{r+1}={r+1\choose 1}h_1 h_2^r=r+1. \end{align*} $$
This completes the proof.
Remark 3.4. The inequality
![]() $d\ge rg+r$
in Theorem 1.1 is sharp. Indeed, the largest possible value of d outside of this range is
$d\ge rg+r$
in Theorem 1.1 is sharp. Indeed, the largest possible value of d outside of this range is
![]() $d=rg$
, corresponding to
$d=rg$
, corresponding to
![]() $d=n-1$
. In this case, following the proof of Theorem 1.1 shows that our intersection of cycles inside
$d=n-1$
. In this case, following the proof of Theorem 1.1 shows that our intersection of cycles inside
![]() $\mathbb {P}^{(r+1)(d+1)-1}$
contains an additional zero-dimensional locus of constant maps
$\mathbb {P}^{(r+1)(d+1)-1}$
contains an additional zero-dimensional locus of constant maps
![]() $[f_0, \ldots , f_r]$
, where each
$[f_0, \ldots , f_r]$
, where each
![]() $f_i$
is a constant multiple of the degree
$f_i$
is a constant multiple of the degree
![]() $d=n-1$
polynomial vanishing at all of the points
$d=n-1$
polynomial vanishing at all of the points
![]() $x_1,\ldots ,x_n$
except one,
$x_1,\ldots ,x_n$
except one,
![]() $x_i$
, and the image of f is the point
$x_i$
, and the image of f is the point
![]() $y_i$
. There is one such map for each of the marked points
$y_i$
. There is one such map for each of the marked points
![]() $x_i$
, so we find that
$x_i$
, so we find that
![]() $L_{g,r,d}=(r+1)^g-n=(r+1)^g-(d+1)$
.
$L_{g,r,d}=(r+1)^g-n=(r+1)^g-(d+1)$
.
Remark 3.5. It is interesting to observe that on a smooth curve C of genus g, a general stable vector bundle E of rank
![]() $r+1$
and degree d has precisely
$r+1$
and degree d has precisely
![]() $(r+1)^g$
line subbundles of maximal degree
$(r+1)^g$
line subbundles of maximal degree
![]() $d'$
, where
$d'$
, where
![]() $d-(r+1)d'=r(g-1)$
(see [Reference Okonek and Teleman16] or [Reference Oxbury17]). The reinterpretation of the numbers
$d-(r+1)d'=r(g-1)$
(see [Reference Okonek and Teleman16] or [Reference Oxbury17]). The reinterpretation of the numbers
![]() $L_{g,r,d}$
from this point of view will be pursued elsewhere.
$L_{g,r,d}$
from this point of view will be pursued elsewhere.
3.2 Proof of Theorem 1.2
We recast the calculation of the previous section in the following light: we consider the incidence correspondence on
![]() $\mathbb {P}^{(r+1)(d+1)-1}\times \operatorname {\mathrm {Gr}}(r+1,d+1)$
of
$\mathbb {P}^{(r+1)(d+1)-1}\times \operatorname {\mathrm {Gr}}(r+1,d+1)$
of
![]() $(r+1)$
-tuples of degree d polynomials, spanning a
$(r+1)$
-tuples of degree d polynomials, spanning a
![]() $r+1$
-dimensional subspace of
$r+1$
-dimensional subspace of
![]() $H^0(\mathbb {P}^1, \mathcal {O}_{\mathbb {P}^1}(d))$
, then pullback Schubert cycle conditions on the Grassmannian side and linear conditions on the projective space side. This incidence correspondence is defined by pulling back the diagonal under the map:
$H^0(\mathbb {P}^1, \mathcal {O}_{\mathbb {P}^1}(d))$
, then pullback Schubert cycle conditions on the Grassmannian side and linear conditions on the projective space side. This incidence correspondence is defined by pulling back the diagonal under the map:
and the condition
![]() $d\ge rg+r$
is needed in order to prevent the indeterminacy locus from being too large. In this section, we obtain formulas for
$d\ge rg+r$
is needed in order to prevent the indeterminacy locus from being too large. In this section, we obtain formulas for
![]() $L_{g,r,d}$
in the cases
$L_{g,r,d}$
in the cases
![]() $r=1$
and
$r=1$
and
![]() $g\ge 1$
by shrinking this base locus.
$g\ge 1$
by shrinking this base locus.
More precisely, for
![]() $j=0,1,\ldots ,r$
, let
$j=0,1,\ldots ,r$
, let
![]() $\rho _{j}\colon \mathbb {P}^{(r+1)(d+1)-1}\dashrightarrow \mathbb {P}^{d}$
be the linear projection remembering
$\rho _{j}\colon \mathbb {P}^{(r+1)(d+1)-1}\dashrightarrow \mathbb {P}^{d}$
be the linear projection remembering
![]() $f_j\in H^0(\mathcal {O}_{\mathbb {P}^1}(d))$
, where we recall that
$f_j\in H^0(\mathcal {O}_{\mathbb {P}^1}(d))$
, where we recall that
![]() $(f_0,\ldots ,f_r)$
is the
$(f_0,\ldots ,f_r)$
is the
![]() $(r+1)$
-tuple of polynomials, whose coefficients are parametrised by
$(r+1)$
-tuple of polynomials, whose coefficients are parametrised by
![]() $\mathbb {P}^{(r+1)(d+1)-1}$
. We now consider the following incidence correspondence:
$\mathbb {P}^{(r+1)(d+1)-1}$
. We now consider the following incidence correspondence:

If
![]() $\mathcal {Q}$
denotes the rank
$\mathcal {Q}$
denotes the rank
![]() $d-r$
tautological quotient bundle on
$d-r$
tautological quotient bundle on
![]() $\operatorname {\mathrm {Gr}}(r+1,d+1)$
, then Z can be realised as the degeneracy locus of the composition:
$\operatorname {\mathrm {Gr}}(r+1,d+1)$
, then Z can be realised as the degeneracy locus of the composition:
and thus has class:
 $$ \begin{align*} \Bigl\{c\bigl(\pi_2^*\mathcal{Q}\bigr)\cdot c\bigl(\pi_1^*\mathcal{O}_{\mathbb{P}^d}(1)\bigr)\Bigr\}_{d-r}=\sum_{i+j=d-r}\pi_2^*\bigl(\sigma_i\bigr)\cdot \pi_1^*\bigl(H^j\bigr)\in \operatorname{{\mathrm{CH}}}^{d-r}\bigl(\mathbb{P}^d\times\operatorname{\mathrm{Gr}}(r+1,d+1)\bigr), \end{align*} $$
$$ \begin{align*} \Bigl\{c\bigl(\pi_2^*\mathcal{Q}\bigr)\cdot c\bigl(\pi_1^*\mathcal{O}_{\mathbb{P}^d}(1)\bigr)\Bigr\}_{d-r}=\sum_{i+j=d-r}\pi_2^*\bigl(\sigma_i\bigr)\cdot \pi_1^*\bigl(H^j\bigr)\in \operatorname{{\mathrm{CH}}}^{d-r}\bigl(\mathbb{P}^d\times\operatorname{\mathrm{Gr}}(r+1,d+1)\bigr), \end{align*} $$
where H is the hyperplane class on
![]() $\mathbb {P}^d$
, and where we have also used that
$\mathbb {P}^d$
, and where we have also used that
![]() $c_j(\mathcal {Q})=\sigma _j$
.
$c_j(\mathcal {Q})=\sigma _j$
.
Because the codimension of the base locus of
![]() $\rho _j$
is
$\rho _j$
is
![]() $d+1>d-r$
, the closure:
$d+1>d-r$
, the closure:
of the pullback of the correspondence Z has the same class, that is,
![]() $\sum _{i+j=d-r} \pi _2^*\bigl (\sigma _i\bigr )\cdot \pi _1^*\bigl (H^j\bigr )$
, where this time
$\sum _{i+j=d-r} \pi _2^*\bigl (\sigma _i\bigr )\cdot \pi _1^*\bigl (H^j\bigr )$
, where this time
![]() $\pi _2\colon \mathbb {P}^{(r+1)(d+1)-1}\times \operatorname {\mathrm {Gr}}(r+1,d+1)\rightarrow \operatorname {\mathrm {Gr}}(r+1,d+1)$
denotes the second projection.
$\pi _2\colon \mathbb {P}^{(r+1)(d+1)-1}\times \operatorname {\mathrm {Gr}}(r+1,d+1)\rightarrow \operatorname {\mathrm {Gr}}(r+1,d+1)$
denotes the second projection.
Proof of Theorem 1.2
We wish to compute the intersection inside
![]() $\mathbb {P}^{(r+1)(d+1)-1}\times \operatorname {\mathrm {Gr}}(r+1,d+1)$
of the
$\mathbb {P}^{(r+1)(d+1)-1}\times \operatorname {\mathrm {Gr}}(r+1,d+1)$
of the
![]() $nr$
linear conditions pulled back from
$nr$
linear conditions pulled back from
![]() $\mathbb {P}^{(r+1)(d+1)-1}$
given by the equations
$\mathbb {P}^{(r+1)(d+1)-1}$
given by the equations
![]() $f(x_i)=y_i$
for
$f(x_i)=y_i$
for
![]() $i=1, \ldots , n$
, the pullback under
$i=1, \ldots , n$
, the pullback under
![]() $\pi _2$
of the Schubert cycles
$\pi _2$
of the Schubert cycles
![]() $\sigma _\lambda $
, where
$\sigma _\lambda $
, where
![]() $\lambda $
is a Schubert index with
$\lambda $
is a Schubert index with
![]() $|\lambda |=rg$
, and the classes of the cycles
$|\lambda |=rg$
, and the classes of the cycles
![]() $Z_0,\ldots , Z_r$
defined above. We proceed as in Lemmas 3.2 and 3.3.
$Z_0,\ldots , Z_r$
defined above. We proceed as in Lemmas 3.2 and 3.3.
First, we introduce the incidence correspondence:

We first claim that the intersection
![]() $\pi _2^*(\sigma _{\lambda })\cdot \pi _1^*({\textbf L})$
in question is supported away from the locus of
$\pi _2^*(\sigma _{\lambda })\cdot \pi _1^*({\textbf L})$
in question is supported away from the locus of
![]() $(f,\Lambda )\in \mathcal {X}$
, where f defines a degenerate map
$(f,\Lambda )\in \mathcal {X}$
, where f defines a degenerate map
![]() $f\colon \mathbb {P}^{1}\to \mathbb {P}^{r'}$
, for some
$f\colon \mathbb {P}^{1}\to \mathbb {P}^{r'}$
, for some
![]() $r'<r$
. When
$r'<r$
. When
![]() $d\ge rg+r$
, the same proof as in Lemma 3.2 applies.
$d\ge rg+r$
, the same proof as in Lemma 3.2 applies.
Suppose that either
![]() $r=1$
or
$r=1$
or
![]() $n=d+2$
, there is such a
$n=d+2$
, there is such a
![]() $(f,\Lambda )\in Z$
in our intersection, and that k of the points
$(f,\Lambda )\in Z$
in our intersection, and that k of the points
![]() $x_1,\ldots ,x_n$
are base points of the
$x_1,\ldots ,x_n$
are base points of the
![]() $r'$
-dimensional linear system
$r'$
-dimensional linear system
![]() $\Lambda _f$
spanned by
$\Lambda _f$
spanned by
![]() $f_0,\ldots ,f_r$
. As in the proof of Lemma 3.2, it must be the case that
$f_0,\ldots ,f_r$
. As in the proof of Lemma 3.2, it must be the case that
![]() $k\ge n-r'-1$
.
$k\ge n-r'-1$
.
Denote the total ramification of
![]() $\Lambda _f$
at
$\Lambda _f$
at
![]() $x_0$
by t. Then,
$x_0$
by t. Then,
 $$ \begin{align*} t&\le \dim\operatorname{\mathrm{Gr}}(r'+1,d-k+1)\\ &\le \dim\operatorname{\mathrm{Gr}}(r'+1,d-n+r'+2)\\ &=(r'+1)(d-n+1). \end{align*} $$
$$ \begin{align*} t&\le \dim\operatorname{\mathrm{Gr}}(r'+1,d-k+1)\\ &\le \dim\operatorname{\mathrm{Gr}}(r'+1,d-n+r'+2)\\ &=(r'+1)(d-n+1). \end{align*} $$
Thus,
 $$ \begin{align*} d&\ge \frac{t}{r'+1}+n-1\\ &=\frac{t}{r'+1}+d+\frac{d}{r}-g, \end{align*} $$
$$ \begin{align*} d&\ge \frac{t}{r'+1}+n-1\\ &=\frac{t}{r'+1}+d+\frac{d}{r}-g, \end{align*} $$
whence
On the other hand, we require that
![]() $\Lambda \in \sigma _\lambda $
, where
$\Lambda \in \sigma _\lambda $
, where
![]() $|\lambda |=rg$
, and
$|\lambda |=rg$
, and
![]() $\Lambda _f\subseteq \Lambda $
. Such a
$\Lambda _f\subseteq \Lambda $
. Such a
![]() $\Lambda $
can only exist if:
$\Lambda $
can only exist if:
as
![]() $\dim (\Lambda /\Lambda _f)=r-r'$
, and each dimension can contribute at most
$\dim (\Lambda /\Lambda _f)=r-r'$
, and each dimension can contribute at most
![]() $d-r$
to the ramification of
$d-r$
to the ramification of
![]() $\Lambda $
at
$\Lambda $
at
![]() $x_0$
. Since
$x_0$
. Since
![]() $r>r'$
, we obtain:
$r>r'$
, we obtain:
 $$ \begin{align*} t+(r-r')\left(rg-\frac{rt}{r'+1}-r\right)&\ge rg\\ t\left(1-\frac{(r-r')r}{r'+1}\right)+(r-r')(rg-r)&\ge rg. \end{align*} $$
$$ \begin{align*} t+(r-r')\left(rg-\frac{rt}{r'+1}-r\right)&\ge rg\\ t\left(1-\frac{(r-r')r}{r'+1}\right)+(r-r')(rg-r)&\ge rg. \end{align*} $$
When
![]() $r=1$
, and thus
$r=1$
, and thus
![]() $r'=0$
, we obtain a contradiction. It remains to consider the case
$r'=0$
, we obtain a contradiction. It remains to consider the case
![]() $n=r+2$
, in which case:
$n=r+2$
, in which case:
Then, comparing the inequalities:
 $$ \begin{align*} t&\le (r'+1)(d-n+1)=(r'+1)(d-r-1)\\ t&\ge rg-(r-r')(d-r)=(d-r)(r+1)-(r-r')(d-r) \end{align*} $$
$$ \begin{align*} t&\le (r'+1)(d-n+1)=(r'+1)(d-r-1)\\ t&\ge rg-(r-r')(d-r)=(d-r)(r+1)-(r-r')(d-r) \end{align*} $$
also yields a contradiction.
Therefore, we are back in the situation of Lemma 3.2, in which all intersection points occur where f is nondegenerate, and in particular,
![]() $(f,\Lambda )$
lies away from the indeterminacy of the
$(f,\Lambda )$
lies away from the indeterminacy of the
![]() $\rho _j$
. The same parameter counts show that f indeed defines a map
$\rho _j$
. The same parameter counts show that f indeed defines a map
![]() $f\colon \mathbb {P}^1\to \mathbb {P}^1$
of degree d with vanishing exactly
$f\colon \mathbb {P}^1\to \mathbb {P}^1$
of degree d with vanishing exactly
![]() $\overline {\lambda }$
at
$\overline {\lambda }$
at
![]() $x_0$
.
$x_0$
.
Furthermore, the intersection in question is transverse by exactly the same argument as in Lemma 3.3, so it suffices to compute the degree of the intersection cycle on
![]() $\mathbb {P}^{(r+1)(d+1)-1}\times \operatorname {\mathrm {Gr}}(r+1,d+1)$
. This equals:
$\mathbb {P}^{(r+1)(d+1)-1}\times \operatorname {\mathrm {Gr}}(r+1,d+1)$
. This equals:
 $$ \begin{align*} \int_{\mathbb{P}^{(r+1)(d+1)-1}\times\operatorname{\mathrm{Gr}}(r+1,d+1)}\pi_2^*\bigl(\sigma_{1^r}^g\bigr) \cdot \pi_1^*\bigl(H^{nr}\bigr) \left(\sum_{i+j=d-r}\pi_2^*\bigl(\sigma_i\bigr)\cdot \pi_1^*\bigl(H^j\bigr)\right)^{r+1} \end{align*} $$
$$ \begin{align*} \int_{\mathbb{P}^{(r+1)(d+1)-1}\times\operatorname{\mathrm{Gr}}(r+1,d+1)}\pi_2^*\bigl(\sigma_{1^r}^g\bigr) \cdot \pi_1^*\bigl(H^{nr}\bigr) \left(\sum_{i+j=d-r}\pi_2^*\bigl(\sigma_i\bigr)\cdot \pi_1^*\bigl(H^j\bigr)\right)^{r+1} \end{align*} $$
 $$ \begin{align*} =\int_{\operatorname{\mathrm{Gr}}(r+1,d+1)}\sigma_{1^r}^g\cdot\left[ \sum_{\alpha_0+\cdots+\alpha_{r}=(r+1)(d-r)-rg}\left(\prod_{i=0}^{r}\sigma_{\alpha_i}\right)\right], \end{align*} $$
$$ \begin{align*} =\int_{\operatorname{\mathrm{Gr}}(r+1,d+1)}\sigma_{1^r}^g\cdot\left[ \sum_{\alpha_0+\cdots+\alpha_{r}=(r+1)(d-r)-rg}\left(\prod_{i=0}^{r}\sigma_{\alpha_i}\right)\right], \end{align*} $$
as desired.
Remark 3.6. While the proof of Theorem 1.2 shows that our refined incidence correspondence avoids the constant maps of Remark 3.1 when
![]() $r=1$
or
$r=1$
or
![]() $n=r+2$
, this is not the case in general. Indeed, suppose that
$n=r+2$
, this is not the case in general. Indeed, suppose that
![]() $r\ge 2$
,
$r\ge 2$
,
![]() $n\ge r+3$
and
$n\ge r+3$
and
![]() $d\ge n-1$
. Then, take
$d\ge n-1$
. Then, take
![]() $f_0,\ldots ,f_r$
to have simple zeroes at
$f_0,\ldots ,f_r$
to have simple zeroes at
![]() $x_1,\ldots ,x_{n-1}$
and an order
$x_1,\ldots ,x_{n-1}$
and an order
![]() $d-(n-1)$
zero at
$d-(n-1)$
zero at
![]() $x_0$
, such that
$x_0$
, such that
![]() $f=[f_0, \ldots , f_r]$
defines the constant map with image
$f=[f_0, \ldots , f_r]$
defines the constant map with image
![]() $y_n\in \mathbb {P}^r$
. If
$y_n\in \mathbb {P}^r$
. If
![]() $\lambda $
is a Schubert index with
$\lambda $
is a Schubert index with
![]() $|\lambda |=rg$
, then the condition that
$|\lambda |=rg$
, then the condition that
![]() $f_0,\ldots ,f_r\in \Lambda $
, where
$f_0,\ldots ,f_r\in \Lambda $
, where
![]() $\Lambda \in \Sigma _\lambda (x_0)\subseteq \operatorname {\mathrm {Gr}}(r+1,d+1)$
, may be satisfied as long as
$\Lambda \in \Sigma _\lambda (x_0)\subseteq \operatorname {\mathrm {Gr}}(r+1,d+1)$
, may be satisfied as long as
![]() $rg\le (d-n+1)+\dim \operatorname {\mathrm {Gr}}(r,d)=(d-n+1)+r(d-r)$
. Substituting
$rg\le (d-n+1)+\dim \operatorname {\mathrm {Gr}}(r,d)=(d-n+1)+r(d-r)$
. Substituting
![]() $rg=dr+r+d-rn$
, this is equivalent to
$rg=dr+r+d-rn$
, this is equivalent to
![]() $n\ge \frac {r^2+r-1}{r-1}=r+2+\frac {1}{r-1}$
. When
$n\ge \frac {r^2+r-1}{r-1}=r+2+\frac {1}{r-1}$
. When
![]() $r\ge 2$
and
$r\ge 2$
and
![]() $n\ge r+3$
, this is immediate.
$n\ge r+3$
, this is immediate.
For
![]() $r=1$
, Theorem 1.2 can be used to recover (via simple manipulations) the explicit formulas in terms of binomial coefficients for the degrees
$r=1$
, Theorem 1.2 can be used to recover (via simple manipulations) the explicit formulas in terms of binomial coefficients for the degrees
![]() $L_{g,1,d}$
. These numbers are also determined in [Reference Cela, Pandharipande and Schmitt5] using excess intersection on Hurwitz spaces of admissible covers.
$L_{g,1,d}$
. These numbers are also determined in [Reference Cela, Pandharipande and Schmitt5] using excess intersection on Hurwitz spaces of admissible covers.
Proposition 3.7. For
![]() $d\geq \frac {g+2}{2}$
, we have:
$d\geq \frac {g+2}{2}$
, we have:
 $$ \begin{align*} L_{g,1,d}&=\sum_{\alpha_0+\alpha_1=2d-2-g}\int_{\operatorname{\mathrm{Gr}}(2,d+1)} \sigma_1^g\cdot \sigma_{\alpha_0}\cdot \sigma_{\alpha_1}\\ &= \sum_{i=0}^{\bigl \lfloor \frac{2d-g-2}{2}\bigr \rfloor} \frac{(2d-g-2i-1)^2}{g+1} {g+1\choose d-i}\\ &=2^g-2\sum_{i=0}^{g-d-1}\binom{g}{i}+(g-d-1)\binom{g}{g-d}+(d-g-1)\binom{g}{g-d+1}, \end{align*} $$
$$ \begin{align*} L_{g,1,d}&=\sum_{\alpha_0+\alpha_1=2d-2-g}\int_{\operatorname{\mathrm{Gr}}(2,d+1)} \sigma_1^g\cdot \sigma_{\alpha_0}\cdot \sigma_{\alpha_1}\\ &= \sum_{i=0}^{\bigl \lfloor \frac{2d-g-2}{2}\bigr \rfloor} \frac{(2d-g-2i-1)^2}{g+1} {g+1\choose d-i}\\ &=2^g-2\sum_{i=0}^{g-d-1}\binom{g}{i}+(g-d-1)\binom{g}{g-d}+(d-g-1)\binom{g}{g-d+1}, \end{align*} $$
where, in the last line, we take
![]() $\binom {g}{j}=0$
when
$\binom {g}{j}=0$
when
![]() $j<0$
.
$j<0$
.
Proof. We use Giambelli’s formula
![]() $\sigma _{a,b}=\sigma _a\cdot \sigma _b-\sigma _{a+1}\cdot \sigma _{b-1}\in \operatorname {{\mathrm {CH}}}^{a+b}\bigl (\operatorname {\mathrm {Gr}}(2,g+1)\bigr )$
for
$\sigma _{a,b}=\sigma _a\cdot \sigma _b-\sigma _{a+1}\cdot \sigma _{b-1}\in \operatorname {{\mathrm {CH}}}^{a+b}\bigl (\operatorname {\mathrm {Gr}}(2,g+1)\bigr )$
for
![]() $a\geq b$
, coupled with the formula (see e.g. [Reference Griffiths and Harris11, p. 269]
$a\geq b$
, coupled with the formula (see e.g. [Reference Griffiths and Harris11, p. 269]
 $$ \begin{align*} \int_{\operatorname{\mathrm{Gr}}(2,d+1)}\sigma_{a,b}\cdot \sigma_1^g&=\frac{a-b+1}{g+1}\cdot\binom{g+1}{d-b}\\ &=\binom{g}{d-b-1}-\binom{g}{d-b} \end{align*} $$
$$ \begin{align*} \int_{\operatorname{\mathrm{Gr}}(2,d+1)}\sigma_{a,b}\cdot \sigma_1^g&=\frac{a-b+1}{g+1}\cdot\binom{g+1}{d-b}\\ &=\binom{g}{d-b-1}-\binom{g}{d-b} \end{align*} $$
for all
![]() $a\geq b$
with
$a\geq b$
with
![]() $a+b=2d-2-g$
. Substituting in the formula provided by Theorem 1.2 yields the claims.
$a+b=2d-2-g$
. Substituting in the formula provided by Theorem 1.2 yields the claims.
3.3 Degrees of determinantal Schubert cycles
We note here that comparison of the incidence correspondences given above in the proofs of Theorems 1.1 and 1.2 allows one to compute the degrees of pullbacks of Schubert cycles of low codimension on
![]() $\operatorname {\mathrm {Gr}}(r+1,d+1)$
to
$\operatorname {\mathrm {Gr}}(r+1,d+1)$
to
![]() $\mathbb {P}^{(r+1)(d+1)-1}$
.
$\mathbb {P}^{(r+1)(d+1)-1}$
.
Proposition 3.8. Let
![]() $\Sigma _{\lambda }$
be a Schubert cycle of codimension
$\Sigma _{\lambda }$
be a Schubert cycle of codimension
![]() $|\lambda |\le d-r$
in
$|\lambda |\le d-r$
in
![]() $\operatorname {\mathrm {Gr}}(r+1,d+1)$
, and let
$\operatorname {\mathrm {Gr}}(r+1,d+1)$
, and let
![]() $\widetilde {\Sigma }_{\lambda }$
be the closure of its pullback under the rational map
$\widetilde {\Sigma }_{\lambda }$
be the closure of its pullback under the rational map
![]() $\pi \colon \mathbb {P}^{(r+1)(d+1)-1}\dashrightarrow \operatorname {\mathrm {Gr}}(r+1,d+1)$
. Then, the degree of
$\pi \colon \mathbb {P}^{(r+1)(d+1)-1}\dashrightarrow \operatorname {\mathrm {Gr}}(r+1,d+1)$
. Then, the degree of
![]() $\widetilde {\Sigma }_{\lambda }$
is:
$\widetilde {\Sigma }_{\lambda }$
is:
 $$ \begin{align*} \int_{\operatorname{\mathrm{Gr}}(r+1,d+1)}\sigma_\lambda\cdot\left[ \sum_{\alpha_0+\cdots+\alpha_{r}-|\lambda|=(r+1)(d-r)-rg}\left(\prod_{i=0}^{r}\sigma_{\alpha_i}\right)\right]. \end{align*} $$
$$ \begin{align*} \int_{\operatorname{\mathrm{Gr}}(r+1,d+1)}\sigma_\lambda\cdot\left[ \sum_{\alpha_0+\cdots+\alpha_{r}-|\lambda|=(r+1)(d-r)-rg}\left(\prod_{i=0}^{r}\sigma_{\alpha_i}\right)\right]. \end{align*} $$
Proof. Let
![]() $N=(r+1)(d+1)-1-|\lambda |$
. Recall that the codimension of
$N=(r+1)(d+1)-1-|\lambda |$
. Recall that the codimension of
![]() $\Sigma _{\lambda }$
is strictly smaller that the codimension of the indeterminacy locus of
$\Sigma _{\lambda }$
is strictly smaller that the codimension of the indeterminacy locus of
![]() $\pi $
. Accordingly, adopting the notation of the previous two sections, we have:
$\pi $
. Accordingly, adopting the notation of the previous two sections, we have:
 $$ \begin{align*} \deg(\widetilde{\Sigma}_{\lambda})&=\int_{\mathbb{P}^{(r+1)(d+1)-1}}H^{N}\cdot[\widetilde{\Sigma}_{\lambda}]\\ &=\int_{\mathbb{P}^{(r+1)(d+1)-1}\times\operatorname{\mathrm{Gr}}(r+1,d+1)}\pi_{1}^{*}\bigl(H^{N}\cdot[\widetilde{\Sigma}_{\lambda}]\bigr)\cdot[Z_0]\cdots[Z_r]\\ &=\int_{\mathbb{P}^{(r+1)(d+1)-1}\times\operatorname{\mathrm{Gr}}(r+1,d+1)}\pi_{1}^{*}\bigl(H^{N}\bigr)\cdot\pi_2^{*}(\Sigma_{\lambda})\cdot[Z_0]\cdots[Z_r]\\ &=\int_{\mathbb{P}^{(r+1)(d+1)-1}\times\operatorname{\mathrm{Gr}}(r+1,d+1)}\pi_{1}^{*}\bigl(H^{N}\bigr)\cdot\pi_2^{*}(\Sigma_{\lambda})\cdot\left(\sum_{i+j=d-r}\pi_2^*\bigl(\sigma_i\bigr) \cdot \pi_1^*\bigl(H^j\bigr)\right)^{r+1}\\ &=\int_{\operatorname{\mathrm{Gr}}(r+1,d+1)}\sigma_\lambda\cdot\left[ \sum_{\alpha_0+\cdots+\alpha_{r}=(r+1)(d-r)-rg-|\lambda|}\left(\prod_{i=0}^{r}\sigma_{\alpha_i}\right)\right], \end{align*} $$
$$ \begin{align*} \deg(\widetilde{\Sigma}_{\lambda})&=\int_{\mathbb{P}^{(r+1)(d+1)-1}}H^{N}\cdot[\widetilde{\Sigma}_{\lambda}]\\ &=\int_{\mathbb{P}^{(r+1)(d+1)-1}\times\operatorname{\mathrm{Gr}}(r+1,d+1)}\pi_{1}^{*}\bigl(H^{N}\cdot[\widetilde{\Sigma}_{\lambda}]\bigr)\cdot[Z_0]\cdots[Z_r]\\ &=\int_{\mathbb{P}^{(r+1)(d+1)-1}\times\operatorname{\mathrm{Gr}}(r+1,d+1)}\pi_{1}^{*}\bigl(H^{N}\bigr)\cdot\pi_2^{*}(\Sigma_{\lambda})\cdot[Z_0]\cdots[Z_r]\\ &=\int_{\mathbb{P}^{(r+1)(d+1)-1}\times\operatorname{\mathrm{Gr}}(r+1,d+1)}\pi_{1}^{*}\bigl(H^{N}\bigr)\cdot\pi_2^{*}(\Sigma_{\lambda})\cdot\left(\sum_{i+j=d-r}\pi_2^*\bigl(\sigma_i\bigr) \cdot \pi_1^*\bigl(H^j\bigr)\right)^{r+1}\\ &=\int_{\operatorname{\mathrm{Gr}}(r+1,d+1)}\sigma_\lambda\cdot\left[ \sum_{\alpha_0+\cdots+\alpha_{r}=(r+1)(d-r)-rg-|\lambda|}\left(\prod_{i=0}^{r}\sigma_{\alpha_i}\right)\right], \end{align*} $$
where we have used the equality:
as subschemes of the incidence correspondence
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
4 Young tableaux interpretation
Comparison of Theorems 1.1 and 1.2 yields the following purely combinatorial statement.
Proposition 4.1. Suppose that
![]() $g\ge 0,r\ge 1,d\ge rg+r$
, and d is divisible by r. Then,
$g\ge 0,r\ge 1,d\ge rg+r$
, and d is divisible by r. Then,
 $$ \begin{align*} \int_{\operatorname{\mathrm{Gr}}(r+1,d+1)}\sigma_{1^r}^g\cdot\left[ \sum_{\alpha_0+\cdots+\alpha_{r}=(r+1)(d-r)-rg}\left(\prod_{i=0}^{r}\sigma_{\alpha_i}\right)\right]=(r+1)^g. \end{align*} $$
$$ \begin{align*} \int_{\operatorname{\mathrm{Gr}}(r+1,d+1)}\sigma_{1^r}^g\cdot\left[ \sum_{\alpha_0+\cdots+\alpha_{r}=(r+1)(d-r)-rg}\left(\prod_{i=0}^{r}\sigma_{\alpha_i}\right)\right]=(r+1)^g. \end{align*} $$
Indeed, both sides are equal to
![]() $L_{g,d,r}$
whenever
$L_{g,d,r}$
whenever
![]() $n=d-g+1+\frac {d}{r}$
is an integer. However, when
$n=d-g+1+\frac {d}{r}$
is an integer. However, when
![]() $d\ge g+r$
, both sides are independent of d; for the left-hand side, this can be seen in terms of Schubert calculus but will also be made transparent in the combinatorial interpretation that follows. In particular, Proposition 4.1 holds under the weaker inequality
$d\ge g+r$
, both sides are independent of d; for the left-hand side, this can be seen in terms of Schubert calculus but will also be made transparent in the combinatorial interpretation that follows. In particular, Proposition 4.1 holds under the weaker inequality
![]() $d\ge g+r$
with no condition on the divisibility by r.
$d\ge g+r$
with no condition on the divisibility by r.
We give a combinatorial interpretation of the left-hand side in terms of a Young tableaux. Consider a filling of the boxes of a
![]() $(r+1)\times (d-r)$
grid with:
$(r+1)\times (d-r)$
grid with:
-
•
 $rg$
red integers among
$rg$
red integers among
 , with each appearing exactly r times, and
, with each appearing exactly r times, and -
•
 $(r+1)(d-r)-rg$
blue integers among
$(r+1)(d-r)-rg$
blue integers among
 , with each appearing any number of times,
, with each appearing any number of times,
subject to the following conditions:
-
• the red integers are top- and left- justified, i.e. they appear above blue integers in the same column and to the left of blue integers in the same row,
-
• the red integers are strictly increasing across rows and weakly increasing down columns, and
-
• the blue integers are weakly increasing across rows and strictly increasing down columns.
An example filling is given in the case
![]() $(g,d,r)=(6,15,2)$
below.
$(g,d,r)=(6,15,2)$
below.

Note that the rightmost
![]() $d-r-g$
columns must be filled with the blue integers
$d-r-g$
columns must be filled with the blue integers
![]() $0,1,\ldots ,r$
in order, so a filling as above is determined by the leftmost g columns, which are those that may contain red integers. In particular, the number of such fillings is independent of d when
$0,1,\ldots ,r$
in order, so a filling as above is determined by the leftmost g columns, which are those that may contain red integers. In particular, the number of such fillings is independent of d when
![]() $d\ge r+g$
. Now, we claim that this number of fillings is given exactly by the intersection number on the left-hand side of Proposition 4.1. Indeed, by the Pieri rule, the term
$d\ge r+g$
. Now, we claim that this number of fillings is given exactly by the intersection number on the left-hand side of Proposition 4.1. Indeed, by the Pieri rule, the term
![]() $\sigma _{1^r}$
corresponds to the transposed semistandard Young tableau given by the red integers, and the broken strips formed by the blue entries equal to i correspond to the Schubert cycle
$\sigma _{1^r}$
corresponds to the transposed semistandard Young tableau given by the red integers, and the broken strips formed by the blue entries equal to i correspond to the Schubert cycle
![]() $\sigma _{\alpha _i}$
.
$\sigma _{\alpha _i}$
.
Proposition 4.1 therefore implies:
Proposition 4.2. Suppose
![]() $d\ge r+g$
. Then, the number of fillings of a
$d\ge r+g$
. Then, the number of fillings of a
![]() $(r+1)\times (d-r)$
grid satisfying the above conditions is equal to
$(r+1)\times (d-r)$
grid satisfying the above conditions is equal to
![]() $(r+1)^g$
.
$(r+1)^g$
.
A combinatorial proof of Proposition 4.2 via the Robinson-Schrensted-Knuth (RSK) algorithm has been given by Gillespie, Reimer and Berg [Reference Gillespie and Reimer-Berg10].
5 Variants
5.1 Linear series with fixed incidences and secancy conditions
We briefly explain how our methods also recover the more general Tevelev degrees of [Reference Cela, Pandharipande and Schmitt5], where some of the points
![]() $x_i$
are constrained to lie in the same fibre of f. Recall from §1 that, if
$x_i$
are constrained to lie in the same fibre of f. Recall from §1 that, if
![]() $1\le k\le n$
, we defined
$1\le k\le n$
, we defined
![]() $L^{\prime }_{g,d,k}$
to be the number of morphisms
$L^{\prime }_{g,d,k}$
to be the number of morphisms
![]() $f\colon C\to \mathbb {P}^1$
of degree d sending general points
$f\colon C\to \mathbb {P}^1$
of degree d sending general points
![]() $x_1,\ldots ,x_n\in C$
to points
$x_1,\ldots ,x_n\in C$
to points
![]() $y_1,\ldots ,y_n\in \mathbb {P}^1$
, where
$y_1,\ldots ,y_n\in \mathbb {P}^1$
, where
![]() $y_1=y_2=\cdots =y_k$
, but the
$y_1=y_2=\cdots =y_k$
, but the
![]() $y_i$
are otherwise general.
$y_i$
are otherwise general.
More generally, we may fix integers
![]() $0\leq a\leq k\leq d$
, a general n-pointed curve
$0\leq a\leq k\leq d$
, a general n-pointed curve
![]() $(C, x_1, \ldots , x_k, x_{k+1},\ldots , x_n)$
of genus g, where n is given by (2), and consider the variety:
$(C, x_1, \ldots , x_k, x_{k+1},\ldots , x_n)$
of genus g, where n is given by (2), and consider the variety:
parametrising linear systems
![]() $\ell $
whose induced map
$\ell $
whose induced map
![]() $\phi _{\ell } \colon C\dashrightarrow \mathbb {P}^r$
has the property that:
$\phi _{\ell } \colon C\dashrightarrow \mathbb {P}^r$
has the property that:
Then
![]() $G^{r,k-a}_{d,k}(C,x_1, \ldots , x_k)$
is a determinantal variety of dimension:
$G^{r,k-a}_{d,k}(C,x_1, \ldots , x_k)$
is a determinantal variety of dimension:
Fixing points
![]() $y_1, \ldots , y_n\in \mathbb {P}^r$
general with the property that:
$y_1, \ldots , y_n\in \mathbb {P}^r$
general with the property that:
one can ask for the number of maps
![]() $f\colon C\rightarrow \mathbb {P}^r$
of degree d, such that
$f\colon C\rightarrow \mathbb {P}^r$
of degree d, such that
![]() $f(x_i)=y_i$
for
$f(x_i)=y_i$
for
![]() $i=1,\ldots , n$
. For any such map, the corresponding linear series
$i=1,\ldots , n$
. For any such map, the corresponding linear series
![]() $\ell :=f^*\bigl |\mathcal {O}_{\mathbb {P}^r}(1)\bigr |$
lies in
$\ell :=f^*\bigl |\mathcal {O}_{\mathbb {P}^r}(1)\bigr |$
lies in
![]() $G^{r,k-a}_{d,k}(C,x_1, \ldots , x_k)$
.
$G^{r,k-a}_{d,k}(C,x_1, \ldots , x_k)$
.
In the interest of simplicity, we deal only with the case:
in which case, this number equals
![]() $L_{g,d,k}'$
. We only sketch the proof; we refer the reader to [Reference Cela and Lian4, §6] for detailed proofs and more general statements.
$L_{g,d,k}'$
. We only sketch the proof; we refer the reader to [Reference Cela and Lian4, §6] for detailed proofs and more general statements.
Proof of Theorem 1.3
Consider a linear series V on our general curve C satisfying the needed incidence conditions. We employ a further degeneration after that of §2, allowing
![]() $x_1,\ldots ,x_k$
to coalesce onto a bubbled rational component
$x_1,\ldots ,x_k$
to coalesce onto a bubbled rational component
![]() $R_k$
, attached to
$R_k$
, attached to
![]() $R_0$
at x, and consider the resulting limit
$R_0$
at x, and consider the resulting limit
![]() $V_0$
on this bubbled curve.Footnote
4
We find that the
$V_0$
on this bubbled curve.Footnote
4
We find that the
![]() $R_k$
-aspect of
$R_k$
-aspect of
![]() $V_0$
must have ramification sequence
$V_0$
must have ramification sequence
![]() $(d-k,d-1)$
at x, and sends
$(d-k,d-1)$
at x, and sends
![]() $x_1,\ldots ,x_k$
to the same point after twisting down the base points at x.
$x_1,\ldots ,x_k$
to the same point after twisting down the base points at x.
It now suffices to count linear series on
![]() $R_0$
with the aggregate ramification condition
$R_0$
with the aggregate ramification condition
![]() $\sigma _1^g$
at
$\sigma _1^g$
at
![]() $x_0$
, the new ramification condition
$x_0$
, the new ramification condition
![]() $\sigma _{k-1}$
at x, an additional linear incidence condition at x (with image
$\sigma _{k-1}$
at x, an additional linear incidence condition at x (with image
![]() $y_1=\cdots =y_k$
) and linear incidence conditions at
$y_1=\cdots =y_k$
) and linear incidence conditions at
![]() $x_{k+1},\ldots ,x_n$
. The computation of §3.2 yields the count:
$x_{k+1},\ldots ,x_n$
. The computation of §3.2 yields the count:
 $$ \begin{align*} \int_{\operatorname{\mathrm{Gr}}(2,d+1)}\sigma_1^g\sigma_{k-1}\cdot\left[\sum_{i+j=2(d-1)-g-(k-1)}\sigma_{i}\sigma_j\right]. \end{align*} $$
$$ \begin{align*} \int_{\operatorname{\mathrm{Gr}}(2,d+1)}\sigma_1^g\sigma_{k-1}\cdot\left[\sum_{i+j=2(d-1)-g-(k-1)}\sigma_{i}\sigma_j\right]. \end{align*} $$
However, we find the following extraneous solutions: if the linear series in question has a base point at x, then we twist down, so that the new ramification sequence is
![]() $(0,k-2)$
, and d decreases by 1; in addition, we lose the linear incidence condition at x. Therefore, we see a (zero-dimensional) excess contribution of:
$(0,k-2)$
, and d decreases by 1; in addition, we lose the linear incidence condition at x. Therefore, we see a (zero-dimensional) excess contribution of:
 $$ \begin{align*} \int_{\operatorname{\mathrm{Gr}}(2,d)}\sigma_1^g\sigma_{k-2}\cdot\left[\sum_{i+j=2(d-2)-g-(k-2)}\sigma_{i}\sigma_j\right]. \end{align*} $$
$$ \begin{align*} \int_{\operatorname{\mathrm{Gr}}(2,d)}\sigma_1^g\sigma_{k-2}\cdot\left[\sum_{i+j=2(d-2)-g-(k-2)}\sigma_{i}\sigma_j\right]. \end{align*} $$
Subtracting the above yields the formula for
![]() $L^{\prime }_{g,d,k}$
. One needs to check that there are no additional degenerate contributions, and that the intersections are transverse as before, but we omit the details.
$L^{\prime }_{g,d,k}$
. One needs to check that there are no additional degenerate contributions, and that the intersections are transverse as before, but we omit the details.
Applying the Pieri rule to the formula of Theorem 1.3 yields the following recursions, recovering [Reference Cela, Pandharipande and Schmitt5, Proposition 7] after the change of coordinates
![]() $\operatorname {\mathrm {Tev}}_{g,\ell ,r}=L^{\prime }_{g,g+\ell +1,r}$
. These recursions are then used in [Reference Cela, Pandharipande and Schmitt5] to obtain explicit formulas in terms of binomial coefficients.
$\operatorname {\mathrm {Tev}}_{g,\ell ,r}=L^{\prime }_{g,g+\ell +1,r}$
. These recursions are then used in [Reference Cela, Pandharipande and Schmitt5] to obtain explicit formulas in terms of binomial coefficients.
Corollary 5.1. We have:
and
for
![]() $k>1$
.
$k>1$
.
Remark 5.2. The proof of Theorem 1.1 may also be employed to show that
![]() $L^{\prime }_{g,d,k}=2^g$
whenever
$L^{\prime }_{g,d,k}=2^g$
whenever
![]() $n\ge d+k+1$
. For general r, the number of linear series in question is
$n\ge d+k+1$
. For general r, the number of linear series in question is
![]() $(r+1)^g$
whenever
$(r+1)^g$
whenever
![]() $n\ge d+a+2$
.
$n\ge d+a+2$
.
However, even when
![]() $r=1$
, the proof of Theorem 1.2 breaks down as soon as
$r=1$
, the proof of Theorem 1.2 breaks down as soon as
![]() $k>1$
, as we will see contributions from constant maps with value
$k>1$
, as we will see contributions from constant maps with value
![]() $y_1=\cdots =y_k$
and base points at
$y_1=\cdots =y_k$
and base points at
![]() $x_{k+1}=\cdots =x_n$
. Thus, the additional degeneration as above is needed to obtain the general formula for
$x_{k+1}=\cdots =x_n$
. Thus, the additional degeneration as above is needed to obtain the general formula for
![]() $L^{\prime }_{g,d,k}$
.
$L^{\prime }_{g,d,k}$
.
5.2 Linear series with imposed incidences and prescribed ramification
We fix a general pointed curve
![]() $[C, p_1,\ldots , p_m, x_1,\ldots ,x_n]\in \mathcal {M}_{g,m+n}$
, general points
$[C, p_1,\ldots , p_m, x_1,\ldots ,x_n]\in \mathcal {M}_{g,m+n}$
, general points
![]() $y_1,\ldots ,y_n\in \mathbb {P}^r$
, as well as m partitions
$y_1,\ldots ,y_n\in \mathbb {P}^r$
, as well as m partitions
![]() $\lambda _1, \ldots , \lambda _m$
of length
$\lambda _1, \ldots , \lambda _m$
of length
![]() $r+1$
. We may consider morphisms
$r+1$
. We may consider morphisms
![]() $f\colon C\to \mathbb {P}^r$
of degree d satisfying
$f\colon C\to \mathbb {P}^r$
of degree d satisfying
![]() $f(x_i)=y_i$
for
$f(x_i)=y_i$
for
![]() $i=1, \ldots , n$
, and f has ramification sequence at least
$i=1, \ldots , n$
, and f has ramification sequence at least
![]() $\overline {\lambda _j}$
at
$\overline {\lambda _j}$
at
![]() $p_j$
for
$p_j$
for
![]() $j=1, \ldots , m$
. Suppose, for simplicity, that the
$j=1, \ldots , m$
. Suppose, for simplicity, that the
![]() $(r+1)$
-st part of each
$(r+1)$
-st part of each
![]() $\lambda _j$
is zero, so that f has no base points. Equivalently, like in (1) we can consider the evaluation map:
$\lambda _j$
is zero, so that f has no base points. Equivalently, like in (1) we can consider the evaluation map:
and ask for its degree when the dimension of the two varieties in question are equal. Using (3), we expect a finite number of such maps
![]() $f\colon C\rightarrow \mathbb {P}^r$
whenever
$f\colon C\rightarrow \mathbb {P}^r$
whenever
![]() $\rho (g,r,d, \overline {\lambda }_1, \ldots , \overline {\lambda }_m)=rn-(r^2+2r)$
, that is, when:
$\rho (g,r,d, \overline {\lambda }_1, \ldots , \overline {\lambda }_m)=rn-(r^2+2r)$
, that is, when:
where
![]() $\lambda _{\operatorname {\mathrm {tot}}}:=|\lambda _1|+\cdots +|\lambda _m|$
is the total size of the partitions
$\lambda _{\operatorname {\mathrm {tot}}}:=|\lambda _1|+\cdots +|\lambda _m|$
is the total size of the partitions
![]() $\lambda _j$
. Let
$\lambda _j$
. Let
![]() $L_{g,r,d}^{\lambda _1,\ldots ,\lambda _m}$
be this number, that is, the degree of the map given by (9).
$L_{g,r,d}^{\lambda _1,\ldots ,\lambda _m}$
be this number, that is, the degree of the map given by (9).
Degenerating the general genus g curve C to a flag curve as in §2 so that the points
![]() $p_1, \ldots , p_m$
specialise to general points on the component
$p_1, \ldots , p_m$
specialise to general points on the component
![]() $R_{\operatorname {\mathrm {sp}}}$
, whereas
$R_{\operatorname {\mathrm {sp}}}$
, whereas
![]() $x_1, \ldots , x_n$
specialise, as before, to general points of the rational component
$x_1, \ldots , x_n$
specialise, as before, to general points of the rational component
![]() $R_0$
, we reduce the computation to the numbers
$R_0$
, we reduce the computation to the numbers
![]() $L_{g,r,d,\lambda }$
, as defined in Definition 2.2, where now
$L_{g,r,d,\lambda }$
, as defined in Definition 2.2, where now
![]() $|\lambda |=rg+\lambda _{\operatorname {\mathrm {tot}}}$
. Following the proof of Theorem 1.1, we obtain the following result.
$|\lambda |=rg+\lambda _{\operatorname {\mathrm {tot}}}$
. Following the proof of Theorem 1.1, we obtain the following result.
Proposition 5.3. Suppose that
![]() $d\ge rg+r+\lambda _{\operatorname {\mathrm {tot}}}$
, or equivalently,
$d\ge rg+r+\lambda _{\operatorname {\mathrm {tot}}}$
, or equivalently,
![]() $n\ge d+2$
. Then,
$n\ge d+2$
. Then,
 $$ \begin{align*} L_{g,r,d}^{\lambda_1,\ldots,\lambda_m}=(r+1)^g\cdot \prod_{j=1}^{m}\deg(\widetilde{\Sigma}_{\lambda_j}), \end{align*} $$
$$ \begin{align*} L_{g,r,d}^{\lambda_1,\ldots,\lambda_m}=(r+1)^g\cdot \prod_{j=1}^{m}\deg(\widetilde{\Sigma}_{\lambda_j}), \end{align*} $$
where
![]() $\deg (\widetilde {\Sigma }_{\lambda _j})$
is the degree of the cycle
$\deg (\widetilde {\Sigma }_{\lambda _j})$
is the degree of the cycle
![]() $\widetilde {\Sigma }_{\lambda _j}$
on
$\widetilde {\Sigma }_{\lambda _j}$
on
![]() $\mathbb {P}^{(r+1)(d+1)-1}$
obtained by taking the closure of the pullback of
$\mathbb {P}^{(r+1)(d+1)-1}$
obtained by taking the closure of the pullback of
![]() $\Sigma _{\lambda _j}(x_0)\subseteq \operatorname {\mathrm {Gr}}(r+1,d+1)$
under the rational map
$\Sigma _{\lambda _j}(x_0)\subseteq \operatorname {\mathrm {Gr}}(r+1,d+1)$
under the rational map
![]() $\pi \colon \mathbb {P}^{(r+1)(d+1)-1}\dashrightarrow \operatorname {\mathrm {Gr}}(r+1,d+1)$
(see Proposition 3.8).
$\pi \colon \mathbb {P}^{(r+1)(d+1)-1}\dashrightarrow \operatorname {\mathrm {Gr}}(r+1,d+1)$
(see Proposition 3.8).
Similarly, closely following the proof of Theorem 1.2, we obtain:
Proposition 5.4. Suppose that:
-
•
 $d\ge rg+r+\lambda _{\operatorname {\mathrm {tot}}}$
,
$d\ge rg+r+\lambda _{\operatorname {\mathrm {tot}}}$
, -
•
 $n=r+2$
, or
$n=r+2$
, or -
•
 $r=1$
.
$r=1$
.
Then,
 $$ \begin{align*} L_{g,r,d}^{\lambda_1,\ldots,\lambda_m}=\int_{\operatorname{\mathrm{Gr}}(r+1,d+1)}\sigma_{1^r}^{g}\cdot\prod_{j=1}^{m}\sigma_{\lambda_j}\cdot\left[ \sum_{\alpha_0+\cdots+\alpha_{r}=(r+1)(d-r)-rg-\lambda_{\operatorname{\mathrm{tot}}}}\left(\prod_{i=0}^{r}\sigma_{\alpha_i}\right)\right]. \end{align*} $$
$$ \begin{align*} L_{g,r,d}^{\lambda_1,\ldots,\lambda_m}=\int_{\operatorname{\mathrm{Gr}}(r+1,d+1)}\sigma_{1^r}^{g}\cdot\prod_{j=1}^{m}\sigma_{\lambda_j}\cdot\left[ \sum_{\alpha_0+\cdots+\alpha_{r}=(r+1)(d-r)-rg-\lambda_{\operatorname{\mathrm{tot}}}}\left(\prod_{i=0}^{r}\sigma_{\alpha_i}\right)\right]. \end{align*} $$
Indeed, in both results, the only significant modification is that the total ramification imposed at
![]() $x_0$
after degeneration is
$x_0$
after degeneration is
![]() $rg+\lambda _{\operatorname {\mathrm {tot}}}$
, instead of
$rg+\lambda _{\operatorname {\mathrm {tot}}}$
, instead of
![]() $rg$
. However, this number is equal to
$rg$
. However, this number is equal to
![]() $dr+d+r-nr$
in both cases, and from here, the proofs go through without change.
$dr+d+r-nr$
in both cases, and from here, the proofs go through without change.
Acknowledgments
This problem was brought to our attention by Rahul Pandharipande. We thank him as well as Alessio Cela and Johannes Schmitt for interesting discussions related to this circle of ideas. We also thank Laurent Manivel and Maria Gillespie for pointing out an error in §4 in an earlier version and communicating alternate proofs of Proposition 4.1, and Benjamin Gunby for help with combinatorial manipulation. Finally, we thank the anonymous referee for numerous improvements.
Gavril Farkas has been supported by the DFG Grant Syzygien und Moduli and by the European Research Council (ERC) Advanced Grant SYZYGY. This project has received funding from the ERC under the European Union Horizon 2020 research and innovation programme (grant agreement No. 834172). Carl Lian was supported by an NSF Postdoctoral Fellowship, grant DMS-2001976.