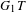Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-06T04:11:24.501Z Has data issue: false hasContentIssue false
  • English
  • Français

THE LOEWY STRUCTURE OF $G_{1}T$-VERMA MODULES OF SINGULAR HIGHEST WEIGHTS

Part of: Linear algebraic groups and related topics

Published online by Cambridge University Press:  02 October 2015

Noriyuki Abe  and
Masaharu Kaneda
Noriyuki Abe
Affiliation:
Creative Research Institution (CRIS), Hokkaido University, Japan (abenori@math.sci.hokudai.ac.jp)
Masaharu Kaneda
Affiliation:
Department of Mathematics, Osaka City University, Japan (kaneda@sci.osaka-cu.ac.jp)
Get access Rights & Permissions [Opens in a new window]

Abstract

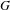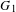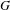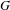Let $G$ be a reductive algebraic group over an algebraically closed field of positive characteristic, $G_{1}$ the Frobenius kernel of $G$, and $T$ a maximal torus of $G$. We show that the parabolically induced 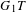$G_{1}T$-Verma modules of singular highest weights are all rigid, determine their Loewy length, and describe their Loewy structure using the periodic Kazhdan–Lusztig $P$- and 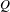$Q$-polynomials. We assume that the characteristic of the field is sufficiently large that, in particular, Lusztig’s conjecture for the irreducible 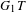$G_{1}T$-characters holds.

Keywords

Frobenius kernelsingular blockLoewy series

MSC classification

Primary: 20G05: Representation theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 16 , Issue 4 , September 2017 , pp. 887 - 898
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, N. and Kaneda, M., On the structure of parabolically induced G 1 T-Verma modules, J. Inst. Math. Jussieu 14(01) (2015), 185–220.Google Scholar
Andersen, H. H., Jantzen, J. C. and Soergel, W., Representations of quantum groups at a p-th root of unity and of semisimple groups in characteristic p: independence of p , Astérisque 220 (1994), 1–321 (SMF).Google Scholar
Andersen, H. H. and Kaneda, M., Loewy series of modules for the first Frobenius kernel in a reductive algebraic group, Proc. Lond. Math. Soc. (3) 59 (1989), 74–98.Google Scholar
Beilinson, A., Ginzburg, D. and Soergel, W., Koszul duality patterns in representation theory, J. Amer. Math. Soc. 9(2) (1996), 473–527.Google Scholar
Bezrukavnikov, R., Mirkovic, I. and Rumynin, D., Singular localization and intertwining functors for reductive Lie algebras in prime characteristic, Nagoya Math. J. 184 (2006), 1–55.Google Scholar
Bezrukavnikov, R., Mirkovic, I. and Rumynin, D., Localization of modules for a semisimple Lie algebra in prime characteristic, Ann. of Math. (2) 167 (2008), 945–991.Google Scholar
Fiebig, P., Lusztig’s conjecture as a moment graph problem, Bull. Lond. Math. Soc. 42(6) (2010), 957–972.Google Scholar
Fiebig, P., An upper bound on the exceptional characteristics for Lusztig’s character formula, J. reine angew. Math. 673 (2012), 1–31.Google Scholar
Irving, R. S., Projective modules in the category 𝓞 S : Loewy series, Trans. Amer. Math. Soc. 291(2) (1985), 733–754.Google Scholar
Irving, R. S., The socle filtration of a Verma module, Ann. Sci. Éc. Norm. Supér. (4) 21 (1988), 47–65.Google Scholar
Jantzen, J. C., Representations of Algebraic Groups (American Mathematical Society, 2003).Google Scholar
Jantzen, J. C., Representations of Lie algebras in prime characteristic, in Representation Theories and Algebraic Geometry (ed. Broer, A.), pp. 185–235 (Kluwer, 1998).Google Scholar
Kaneda, M., The Kazhdan–Lusztig polynomials arising in the modular representation theory of reductive algebraic groups, RIMS Kōkyūroku 670 (1988), 129–162.Google Scholar
Kato, S., On the Kazhdan–Lusztig polynomials for affine Weyl groups, Adv. Math. 55 (1995), 103–130.Google Scholar
Lusztig, G., Hecke algebras and Jantzen’s generic decomposition patterns, Adv. Math. 37 (1980), 121–164.Google Scholar
Riche, S., Koszul duality and modular representations of semisimple Lie algebras, Duke Math. J. 154 (2010), 31–134.Google Scholar
Williamson, G., Kontorovich, A. and McNamara, P., Schubert calculus and torsion explosion, arXiv:1309.5055v2.Google Scholar