NORMALISED TANGENT BUNDLE, VARIETIES WITH SMALL CODEGREE AND PSEUDOEFFECTIVE THRESHOLD

Abstract

We propose a conjectural list of Fano manifolds of Picard number 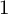$1$ with pseudoeffective normalised tangent bundles, which we prove in various situations by relating it to the complete divisibility conjecture of Francesco Russo and Fyodor L. Zak on varieties with small codegree. Furthermore, the pseudoeffective thresholds and, hence, the pseudoeffective cones of the projectivised tangent bundles of rational homogeneous spaces of Picard number 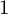$1$ are explicitly determined by studying the total dual variety of minimal rational tangents (VMRTs) and the geometry of stratified Mukai flops. As a by-product, we obtain sharp vanishing theorems on the global twisted symmetric holomorphic vector fields on rational homogeneous spaces of Picard number 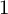$1$.

1 Introduction

1.A Positivity of normalised tangent bundles

Let X be an n-dimensional projective manifold, and let $C\subset X$ be an irreducible projective curve. The (semi)stability of the restriction $T_X|_C$ is very closely related to the global geometry of X. For example, a famous result of Mehta and Ramanathan [33] says that the restriction $T_X|_C$ of $T_X$ to a general complete intersection curve C of sufficiently ample divisors is again (semi)stable provided that $T_X$ itself is (semi)stable with the respective polarisation. However, apart from very special situations, the variety X usually contains many dominating families of irreducible curves to which the restrictions of $T_X$ are not (semi)stable. Using the language of positivity of $\mathbb {Q}$ -twisted vector bundles, the semistability of $T_X|_C$ is equivalent to the nefness of the restriction of the normalised tangent bundle $T_X\hspace {-0.8ex}<\hspace {-0.8ex}-\frac {1}{n}c_1(X)\hspace {-0.8ex}>$ of X to C (see [29, Proposition 6.4.11]). Thus, our expectation above can be rephrased by saying that X should be very special if its normalised tangent bundle is positive in some algebraic sense.

Let $\pi :\mathbb {P}(T_X)\rightarrow X$ be the projectivised tangent bundle (in the Grothendieck sense) with tautological divisor $\Lambda $ . The normalised tangent bundle $T_X\hspace {-0.8ex}<\hspace {-0.8ex}-\frac {1}{n}c_1(X)\hspace {-0.8ex}>$ is said pseudoeffective (respectively, ample, big, nef), if so, is the class $\Lambda - \frac {1}{n} \pi ^* (c_1(X))$ . The normalised tangent bundle is said almost nef if all irreducible curves $C \subset X$ , to which the restriction of $T_X\hspace {-0.8ex}<\hspace {-0.8ex}-\frac {1}{n}c_1(X)\hspace {-0.8ex}>$ is not nef, are contained in a countable union of proper subvarieties of X. Since the normalised tangent bundle of a curve is numerically trivial, we will only consider varieties of dimension at least 2.

The positivity of normalised tangent bundles has already been studied in various contexts. In particular, we have the following theorem, which can be easily derived from the works of Höring-Peternell [16, Theorem 1.9], Jahnke-Radloff [23, Theorem 0.1] and Liu-Ou-Yang [32, Theorem 1.6]. It can be viewed as a strong evidence to our expected picture above.

Theorem 1.1. Let X be a projective manifold of dimension at least 2. Then the normalised tangent bundle of X is almost nef if and only if X is isomorphic to a finite étale quotient of an Abelian variety.

The motivation of this paper is to study a weaker positivity: the pseudoeffectivity of normalised tangent bundles. This problem has already been studied by Höring-Peternell in [16] for Kawamata log terminal (klt) projective variety with numerically trivial canonical class. Moreover, Nakayama has studied this problem in [38] for semi-stable vector bundles of rank $2$ over projective manifolds of arbitrary dimension, and he obtained a complete classification for such vector bundles (see [38, IV, Theorem 4.8] for a precise statement). In particular, Nakayama’s result provides a satisfactory answer to our problem above for projective surfaces. For instance, it turns out that a del Pezzo surface S has pseudoeffective normalised tangent bundle if and only if S is isomorphic to a quadric surface (see Theorem 4.8). Note that the product of two projective manifolds with pseudoeffective normalised tangent bundle has again pseudoeffective normalised tangent bundle. To exclude the product cases, we will focus on the case where X is a Fano manifold of Picard number $1$ with dimension at least $3$ in this paper. Note that in this situation, the pseudoeffectivity of the normalised tangent bundle of X implies that the tangent bundle of X is big, and it is expected that the bigness of the tangent bundle is already a rather restrictive property (see [15]). We expect the following classification:

Conjecture 1.2. Let X be a Fano manifold of Picard number $1$ with dimension at least $3$ . Then the normalised tangent bundle of X is pseudoeffective if and only if X is one of the following varieties:

1. (1) a smooth quadric hypersurface;

2. (2) the Grassmann variety $\mathrm {Gr}(n,2n)$ ;

3. (3) the spinor variety $\mathbb {S}_{2n}$ ;

4. (4) the Lagrangian Grassmann variety $\mathrm LG(n,2n)$ ;

5. (5) the $27$ -dimensional $E_7$ -variety $E_7/P_7$ .

Note that the normalised tangent bundles of the varieties in the list are already shown to be pseudoeffective but not big by [47, Corollary 1.4] (see Proposition 5.14 for another proof). We will prove a more general result in Theorem 1.14. On the other hand, if we use the pseudoeffective threshold (with respect to an ample line bundle A) introduced in [47] which is defined as:

$$\begin{align*}\alpha(X,A):= \mathrm{sup} \{\alpha \in \mathbb{R}\, |\, \Lambda - \alpha \pi^*A\ \text{is effective} \},\end{align*}$$

then we can reformulate Conjecture 1.2 as follows:

Conjecture 1.3. Let X be a Fano manifold of Picard number $1$ with dimension at least $3$ . Then:

$$\begin{align*}\alpha(X,-K_X)\leq \frac{1}{\dim(X)} \end{align*}$$

with equality if and only if X is one of the varieties in Conjecture 1.2.

Remark 1.4. By Theorem 1.1, the normalised tangent bundle of a projective manifold can not be nef and big (see also [38, IV, Corollary 4.7]). On the other hand, Conjecture 1.2 implies that there does not exist examples of Fano manifolds of Picard number $1$ with big normalised tangent bundle, and we suspect the existence of such examples even for Fano manifolds of higher Picard number. Here, we recall that if the tangent bundle $T_X$ of a Fano manifold X is semistable with respect to some ample line bundle A, then the normalised tangent bundle of X can not be big (see Lemma 2.8).

A powerful tool to study Fano manifolds is the variety of minimal rational tangents (VMRT) theory developed by Hwang and Mok (cf. [18]). Fix a dominating family of minimal rational curves $\mathcal {K}$ on a Fano manifold X and a general point $x \in X$ . The tangent directions at x of members in $\mathcal {K}$ passing through x form a projective subvariety $\mathcal {C}_x$ in $\mathbb {P}(\Omega _{X,x})$ . The projective geometry of $\mathcal {C}_x$ encodes many global properties of X. For example, we can recover irreducible Hermitian symmetric spaces (IHSS for short) from their VMRTs by the following result of Mok:

Theorem 1.5 (34, Main Theorem)

Let $G/P$ be an irreducible Hermitian symmetric space, and let X be a Fano manifold of Picard number $1$ . Assume that the VMRT of X at a general point is projectively equivalent to that of $G/P$ . Then X is isomorphic to $G/P$ .

As all the varieties listed in Conjecture 1.2 are IHSS, we may try to determine first the VMRTs of X in Conjecture 1.2, and then apply Theorem 1.5. This is the approach that we will use in this paper.

It is interesting to remark that among IHSS, only the following varieties do not appear in Conjecture 1.2: $\mathrm {Gr}(a, a+b) $ with $a \neq b$ , $\mathbb {S}_{2n+1}$ and $E_6/P_1$ . These varieties are exactly those among IHSS which appear in stratified Mukai flops (cf. Proposition 5.2). As it will become clearer, there exists a delicate relationship between the pseudoeffective threshold and the birational geometry.

1.B Varieties with small codegree

Recall that the codegree $\operatorname *{\mathrm {codeg}}(Z)$ of a projective variety $Z\subset \mathbb {P}^N$ is defined as the degree of its dual variety $\check {Z}\subset \check {\mathbb {P}}^N$ (see Definition 3.1). Varieties with small degree have been thoroughly studied, while very little is known for varieties with small codegree. Segre proved in [46] that for an irreducible and linearly nondegenerate projective variety $Z\subsetneq \mathbb {P}^N$ , if its dual variety $\check {Z}\subset \check {\mathbb {P}}^N$ is a hypersurface with nonvanishing hessian, then we have the following Segre inequality:

(1.1) $$ \begin{align} \operatorname*{\mathrm{codeg}}(Z):=\deg(\check{Z})\geq \frac{2(N+1)}{\dim(Z)+2}. \end{align} $$

The above inequality is sharp, and, in fact, the following complete divisibility conjecture due to Russo and Zak predicts the boundary varieties:

Conjecture 1.6 ([45, Question 5.3.11] [56, Conjecture 4.15])

Let $Z\subsetneq \mathbb {P}^N$ be an irreducible and linearly nondegenerate projective variety. If the dual variety $\check {Z}\subset \check {\mathbb {P}}^N$ is a hypersurface with nonvanishing hessian, such that:

(1.2) $$ \begin{align} \operatorname*{\mathrm{codeg}}(Z):=\deg(\check{Z})=\frac{2(N+1)}{\dim(Z)+2}, \end{align} $$

then Z is isomorphic to one of the following varieties:

1. (1) a smooth quadric hypersurface ( $\operatorname *{\mathrm {codeg}}(Z)=2$ );

2. (2) the Segre variety $\mathbb {P}^{n-1}\times \mathbb {P}^{n-1}\subset \mathbb {P}^{(n-1)(n+1)}$ ( $\operatorname *{\mathrm {codeg}}(Z)=n$ );

3. (3) the Grassmann variety $\mathrm {Gr}(2,2n)\subset \mathbb {P}^{n(2n-1)-1}$ ( $\operatorname *{\mathrm {codeg}}(Z)=n$ );

4. (4) the Veronese variety $\nu _2(\mathbb {P}^{n-1})\subset \mathbb {P}^{\frac {(n-1)(n+2)}{2}}$ ( $\operatorname *{\mathrm {codeg}}(Z)=n$ );

5. (5) the $16$ -dimensional Cayley plane $E_6/P_1\subset \mathbb {P}^{26}$ ( $\operatorname *{\mathrm {codeg}}(Z)=3$ ).

Conjecture 1.6 is still widely open for $\operatorname *{\mathrm {codeg}}(Z) \geq 4$ . The case $\operatorname *{\mathrm {codeg}}(Z)=2$ is easy, as Z must be a hyperquadric. When $\operatorname *{\mathrm {codeg}}(Z)=3$ , then we have $\dim Z = \frac {2N-4}{3}$ , which is the bound for Severi varieties. Thanks to Zak’s classification of smooth varieties of codegree $3$ (see [55, Theorem 5.2]), it turns out in this case, Z is one of the following Severi varieties:

$$ \begin{align*} \nu_2(\mathbb{P}^2) \subset \mathbb{P}^5, \qquad \mathbb{P}^2 \times \mathbb{P}^2 \subset \mathbb{P}^8, \qquad \mathrm{Gr}(2,6) \subset \mathbb{P}^{14} or \qquad E_6/P_1\subset \mathbb{P}^{26}. \end{align*} $$

As a corollary, Conjecture 1.6 is confirmed in the following two cases:

1. (1) $\dim (Z)>\frac {2N-4}{3}$ ;

2. (2) Z is smooth and $\dim (Z)>\frac {N-3}{2}$ .

On the other hand, initiated from the 1950s, there have been many efforts trying to classify nonsingular curves and surfaces with small codegree, which proves Conjecture 1.6 up to dimension $2$ . More precisely, we have:

Proposition 1.7 ([51, Theorem 2.1] [56, Propositions 3.1 and 3.2])

If $Z\subsetneq \mathbb {P}^N$ is a smooth projective variety of dimension at most $2$ satisfying (1.2), then Z is either a conic curve, a quadric surface or the Veronese surface $\nu _2(\mathbb {P}^2)\subset \mathbb {P}^5$ .

There are very few papers devoted to threefold cases (see, for example, [27]). We will confirm Conjecture 1.6 for smooth projective threefolds. More precisely we shall show:

Proposition 1.8. Let $Z\subsetneq \mathbb {P}^N$ be a linearly nondegenerate smooth projective threefold of degree d and codegree $d^*$ . Then one of the following statements holds:

1. (1) $p_g(S)\not =0$ and $d^*\geq 2N$ , where S is a general hyperplane section of Z.

2. (2) $2d^*\geq d$ with equality if and only if Z is projectively equivalent to either the Veronese variety $\nu _2(\mathbb {P}^3)\subset \mathbb {P}^9$ or its isomorphic projection in $\mathbb {P}^8$ .

In particular, Conjecture 1.6 holds for smooth projective threefolds. More precisely, if $Z\subsetneq \mathbb {P}^N$ is a linearly nondegenerate smooth projective threefold satisfying the equality (1.2), then Z is either a quadric threefold in $\mathbb {P}^4$ or the Veronese embedding $\nu _2(\mathbb {P}^3)\subset \mathbb {P}^9$ .

The relation between Conjectures 1.2 and 1.6 can be easily seen from Table 1 above: the varieties listed in Conjecture 1.6 are nothing else but the VMRTs of the varieties listed in Conjecture 1.2. Indeed, if we assume that the VMRT of X at a general point is not dual defective, then the pseudoeffectivity of the normalised tangent bundle can be interpreted as information on the cohomological class of the total dual VMRT (cf. [15, 22]). This allows us to relate Conjectures 1.2 to 1.6. In particular, combining this with the known results for Conjecture 1.6 yields the following first main result of this paper.

Theorem 1.9. Let X be an n-dimensional Fano manifold of Picard number $1$ with $n\geq 3$ . Assume that the VMRT ${\mathcal C}_x\subset \mathbb {P}(\Omega _{X,x})$ at a general point $x\in X$ is not dual defective.

1. (1) If we assume in addition that the VMRT is irreducible and linearly nondegenerate, such that its dual variety has nonvanishing hessian, then:

   • (1.1) $\alpha (X,-K_X)\leq \frac {1}{\dim (X)}$ ;

   • (1.2) Conjecture 1.6 implies Conjectures 1.2 and, hence, 1.3;

2. (2) Conjectures 1.2 and 1.3 hold if one of the following holds:

   • (2.1) $\dim ({\mathcal C}_x)>\frac {2n-6}{3}$ ;

   • (2.2) ${\mathcal C}_x$ is smooth and $\dim ({\mathcal C}_x)>\max \left \{\frac {n-4}{2},0\right \}$ or

   • (2.3) ${\mathcal C}_x$ is irreducible, smooth, linearly nondegenerate and $\dim ({\mathcal C}_x)\leq 3$ .

Table 1 IHSS and their VMRTs.

Our statement is actually a bit stronger: if in Theorem 1.9, the normalised tangent bundle of X is assumed to be pseudoeffective, then the VMRT ${\mathcal C}_x\subset \mathbb {P}(\Omega _{X,x})$ satisfies the reverse Segre inequality (1.1) (see Proposition 4.3). Typically, a projective variety is dual defective only in very special cases and the VMRTs of a large class of Fano manifolds are smooth and irreducible. Thus, the assumption on smoothness, irreducibility and nondefectiveness is not very restrictive. However, the assumption on the nondegeneracy seems to be a strong restriction as many known examples of Fano manifolds have degenerate VMRTs.

Corollary 1.10. Let X be an n-dimensional Fano manifold of Picard number $1$ , such that $3\leq n\leq 5$ . Assume that the VMRT ${\mathcal C}_x\subset \mathbb {P}(\Omega _{X,x})$ at a general point is smooth and nonlinear. Then the normalised tangent bundle of X is pseudoeffective if and only if X is a smooth quadric hypersurface in $\mathbb {P}^{n+1}$ ( $3\leq n\leq 5$ ).

Remark 1.11. Let X be a Fano manifold of Picard number $1$ . To the best of our knowledge, the known examples of X with singular VMRTs have dimension at least $6$ (cf. [19, Theorem 1.3]) and the known examples of X, not isomorphic to projective spaces, with linear VMRTs also have dimension at least $6$ (cf. [36, Proposition A.8]).

Corollary 1.12. Let X be an n-dimensional Fano manifold of Picard number $1$ , such that $3\leq n\leq 11$ . Assume that the VMRT ${\mathcal C}_x$ at a general point $x\in X$ is irreducible, smooth, linearly nondegenerate and not dual defective. Then the normalised tangent bundle of X is pseudoeffective if and only if X is one of the following varieties:

1. (1) a smooth quadric hypersurface in $\mathbb {P}^{n+1}$ ( $3\leq n\leq 11$ );

2. (2) the Lagrangian Grassmann varieties $\mathrm LG(3,6)$ and $\mathrm LG(4,8)$ or

3. (3) the Grassmann variety $\mathrm {Gr}(3,6)$ .

1.C Rational homogeneous spaces

As mentioned in the previous subsection, the pseudoeffectivity of the normalised tangent bundle implies the bigness of the tangent bundle and, to our knowledge, there are very few known examples of Fano manifolds of Picard number $1$ with big tangent bundle. Apart from rational homogeneous spaces, only two examples are known, namely, the del Pezzo threefold $V_5$ of degree $5$ [15, Theorem 1.5] and the horospherical $G_2$ -variety $\mathbb {X}$ [44, Theorem 2.3] (see Remark 6.4 and [31]). Thus, a natural question is to verify Conjecture 1.2 for those examples. This is more or less equivalent to determine the pseudoeffective cone of the projectivised tangent bundle, or equivalently, to determine the invariant $\alpha (X,-K_X)$ , and it fits into the following general problem in the study of positivity of vector bundles.

Problem 1.13 (38, IV.4, Problem)

Let E be a vector bundle over a projective manifold X, and let $\Lambda $ be the tautological class of the projectivised bundle $\pi :\mathbb {P}(E)\rightarrow X$ . Describe the set:

$$\begin{align*}V(X,E):=\{ D\in N^1(X)\,|\, \Lambda+\pi^*D\ \text{is pseudoeffective}\}. \end{align*}$$

The second part of this paper is devoted to study Problem 1.13 for rational homogeneous spaces $X=G/P$ of Picard number $1$ and for $E=T_{X}$ . This is equivalent to determine whether the following cohomological group:

$$\begin{align*}H^0(X,(\mathrm{Sym}^r T_X)\otimes {\mathcal O}_X(-dH)) \end{align*}$$

vanishes or not, where H is the ample generator of $\mathrm {Pic}(X)$ . In general, it is quite difficult to compute these cohomological groups due to the lack of tools. However, recently it is observed in [15] that the problem can be translated into the calculation of the cohomological class of the total dual VMRT if the VMRT is not dual defective. By combining this with the geometry of stratified Mukai flops, we will completely settle Problem 1.13 for rational homogeneous spaces of Picard number 1 with E being the tangent bundle, which reads as follows:

Theorem 1.14. Let $G/P$ be a rational homogeneous space of Picard number 1 with dimension at least $2$ . Let $\Lambda $ be the tautological divisor on $\mathbb {P}(T_{G/P})$ and $\pi : \mathbb {P}(T_{G/P}) \to G/P$ be the natural projection. Denote by H the ample generator of $\operatorname *{\mathrm {Pic}}(G/P)$ . Then there exist two integers $a, b$ (explicitly determined in Appendix A) associated to $G/P$ , such that:

1. (1) The pseudoeffective threshold $\alpha (G/P,H)$ is equal to $b/a$ , namely, $\Lambda - \lambda \pi ^* H$ is pseudoeffective if and only if $\lambda \leq b/a$ .

2. (2) Let r and d be two arbitrary positive integers. Then:

   $$\begin{align*}H^0(G/P, (\mathrm{Sym}^r T_{G/P})\otimes {\mathcal O}_{G/P}(-dH))\not=0 \Longleftrightarrow b \left \lfloor \frac{r}{a} \right \rfloor\geq d; \end{align*}$$

3. (3) Conjecture 1.2 and, hence, Conjecture 1.3 hold for $G/P$ .

Note that Shao proved in [47], with completely different techniques (via the Borel-Weil-Bott Theorem), the statements of Theorem 1.14 for IHSS. It seems hard to extend his arguments to this general setting.

The main idea of the proof is to use the generically finite Springer map $\widehat {s}: T^*_{G/P}\rightarrow \overline {{\mathcal O}}$ from the cotangent bundle of $G/P$ to its Richardson orbit closure. By taking the Stein factorisation, and then taking the projectivisation, we get a birational map $\varepsilon : \mathbb {P} (T_{G/P}) \to \mathcal {Y} $ . The birational geometry of $\varepsilon $ is well understood ([10], [39], [40]), which implies, for example, when $\varepsilon $ is small, there exists a (projectivised) stratified Mukai flop (over $\mathcal {Y}$ ) with $G/P \simeq G/Q$ . This allows us to determine the effective cone and the movable cone of $\mathbb {P} (T_{G/P})$ (cf. Theorem 5.5) in terms of the exceptional divisor $\Gamma $ of $\varepsilon $ (respectively, $\mu ^* \pi _2^* H$ ) when $\varepsilon $ is divisorial (respectively, when $\varepsilon $ is small), where $\pi _2: \mathbb {P} (T_{G/Q}) \to G/Q$ and H is an ample generator of $\operatorname *{\mathrm {Pic}}(G/Q)$ . The two numbers a and b in Theorem 1.14 are the unique positive integers, such that:

$$ \begin{align*} \Gamma \equiv a \Lambda - b \pi^*H \quad (\text{resp. } \mu^*\pi_2^*H \equiv a \Lambda - b \pi_1^*H). \end{align*} $$

It turns out the integer a is very geometrical, which is related to the codegree of the VMRT of $G/P$ or to the degree of the images of lines under the stratified Mukai flops, while b is an integer taking value $1$ or $2$ , and $b=2$ if and only if the VMRT of $G/P$ is not dual defective and $G/P$ is not isomorphic to $E_7/P_4$ . Subsequently, we will divide $G/P$ into different types (Definition 5.6). In order to compute them, we carry out a detailed study of stratified Mukai flops.

One interesting observation is that we have $(a,b)=(4,2)$ for Fano contact manifolds of Picard number $1$ different to projective spaces (cf. Proposition 5.14), and their VMRTs are the homogeneous Legendre varieties, which form the main series of the conjectural list of nonsingular varieties with codegree $4$ and are also the examples of varieties of next to minimal degree (cf. [50, p. 168] and [56, Remarks 3.6 and 4.16]).

Other interesting examples of Fano manifolds with Picard number $1$ are provided by moduli spaces $\text {SU}_C(r,d)$ of stable vector bundles of rank r and degree d over a nonsingular projective curve of genus g. Based on the work of Hwang-Ramanan [22], we show in Corollary 3.5 that the tangent bundle of $\text {SU}_C(r,d)$ is not big if $g\geq 4$ , $r\geq 3$ and $(r,d)=1$ . In particular, the normalised tangent bundle of $\text {SU}_C(r,d)$ is not pseudoeffective in this case.

Remark 1.15. As predicted by Conjecture 1.2, a Fano manifold of Picard number 1 with pseudoeffective normalised tangent bundle must have nef tangent bundle. If we can prove this, then Conjecture 1.2 would follow from Theorem 1.14 and the famous Campana-Peternell conjecture (see [5]), which predicts that Fano manifolds with nef tangent bundles must be homogeneous.

Here is the organization of this paper: after a brief recall of various notions of positivity of vector bundles in Section 2, we describe in Section 3 the pseudoeffective cone of $\mathbb {P}(T_X)$ in terms of total dual VMRT when X is a Fano manifold of Picard number $1$ with a big tangent bundle whose VMRT is not dual defective. Section 4 is devoted to the proof of Theorem 1.9. We determine the pseudoeffective cone of $\mathbb {P}(T_{G/P})$ in Section 5 for rational homogeneous spaces $G/P$ of Picard number $1$ . Two nonhomogeneous examples are studied in Section 6.

2 Cone of divisors and positivity of vector bundles

2.A Cone of divisors

Given a projective variety X, we consider the real vector space $N^1(X):=N^1_{\mathbb {R}}(X)$ of Cartier divisors, with real coefficients, up to numerical equivalence. Its dimension is equal to the Picard number $\rho (X)$ of X. This vector space contains several important convex cones.

1. (1) The effective cone $\mathrm {Eff}(X)$ is the convex cone in $N^1(X)$ generated by classes of effective divisors. This cone is neither closed nor open in general. The closure $\overline {\mathrm {Eff}}(X)$ of $\mathrm {Eff}(X)$ is called the pseudoeffective cone of X. The interior of the effective cone $\mathrm {Eff}(X)$ is the big cone $\mathrm {Big}(X)$ of X, which is the convex cone generated by big $\mathbb {R}$ -Cartier divisors.

2. (2) Denote by $\mathrm {Mov}(X)$ the cone in $N^1(X)$ generated by classes of movable divisors; that is, Cartier divisors D on X, such that its stable base locus ${\mathbb B}(D)$ has codimension at least 2. Again, this cone is neither closed nor open. The closure $\overline {\mathrm {Mov}}(X)$ of $\mathrm {Mov}(X)$ is called the movable cone. Recall that the stable base locus of a $\mathbb {Q}$ -Cartier $\mathbb {Q}$ -Weil divisor D on a projective variety X is the Zariski closed subset defined as:

   $$\begin{align*}{\mathbb B}(D) := \bigcap_{m\in \mathbb{N},\ mD\ \mathrm{Cartier}} \mathrm{Bs}(mD). \end{align*}$$

3. (3) The nef cone $\mathrm {Nef}(X)$ is the cone of classes in $N^1(X)$ having nonnegative intersection with all curves in X. This cone is closed by definition, and its interior is the ample cone $\mathrm {Amp}(X)$ , which is generated by classes of ample divisors. In general, the nef cone is neither polyhedral nor rational.

Clearly, there are inclusions: $\mathrm {Nef}(X)\subseteq \overline {\mathrm {Mov}}(X) \subseteq \overline {\mathrm {Eff}}(X)$ .

2.B Divisorial Zariski decomposition

Let D be a pseudoeffective $\mathbb {R}$ -divisor on a smooth projective variety X. Recall that for a prime divisor $\Gamma $ on X, we can define:

$$\begin{align*}\sigma_{\Gamma}(D)=\lim_{\epsilon\to 0^+} \inf \,\{\text{Mult}_{\Gamma} D'\, |\, D'\geq 0\ \mathrm{and}\ D'\sim_{\mathbb{R}} D+\epsilon A\}, \end{align*}$$

where A is any fixed ample divisor. By [38, III, Corollary 1.11], there are only finitely many prime divisors $\Gamma $ on X, such that $\sigma _{\Gamma }(D)>0$ . This allows us to make the following definition (see [4] and [38, III]).

Definition 2.1. Let D be a pseudoeffective $\mathbb {R}$ -divisor on a projective manifold X. Define:

$$ \begin{align*} N_{\sigma}(D)=\sum_{\Gamma} \sigma_{\Gamma}(D) \Gamma \quad \text{and} \quad P_{\sigma}(D)=D-N_{\sigma}(D). \end{align*} $$

The decomposition $D=N_{\sigma }(D)+P_{\sigma }(D)$ is called the divisorial Zariski decomposition of D.

Note that $N_{\sigma }(D)$ is an effective $\mathbb {R}$ -Weil divisor and $P_{\sigma }(D)$ is a movable $\mathbb {R}$ -divisor, that is, $[P_{\sigma }(D)]\in \overline {\mathrm {Mov}}(X)$ (cf. [38, III, Proposition 1.14]). In particular, for any prime divisor $\Gamma \subset X$ , the restriction $P_{\sigma }(D)|_{\Gamma }$ is pseudoeffective.

2.B.1 Augmented and restricted base loci

Let D be an $\mathbb {R}$ -Cartier $\mathbb {R}$ -Weil divisor on a normal projective variety X. The augmented base locus (a.k.a., nonample locus) of D is defined to be:

$$\begin{align*}{\mathbb B}_+(D):=\bigcap_{A}{\mathbb B}(D-A), \end{align*}$$

where the intersection is over all ample divisors A, such that $D-A$ is a $\mathbb {Q}$ -Cartier $\mathbb {Q}$ -Weil divisor. The restricted base locus (a.k.a., nonnef locus) of D is defined as:

$$\begin{align*}{\mathbb B}_{-}(D):=\bigcup_{A}{\mathbb B}(D+A), \end{align*}$$

where the union is taken over all ample divisors A, such that $D+A$ is a $\mathbb {Q}$ -Cartier $\mathbb {Q}$ -Weil divisor. Recall that the augmented and restricted base loci depend only on the numerical equivalence class of D, and we refer the reader to [8] for a detailed discussion of these notions. Let us denote by ${\mathbb B}_{+}^1(D)$ (respectively, ${\mathbb B}_{-}^1(D)$ ) the union of codimension $1$ components of ${\mathbb B}_{+}(D)$ (respectively, ${\mathbb B}_{-}(D))$ .

Lemma 2.2. Let D and $D'$ be two pseudoeffective $\mathbb {R}$ -Cartier $\mathbb {R}$ -Weil divisors on a normal projective variety X. Assume that there exists an ample divisor A, such that $[D]$ is contained in the interior of the two-dimensional cone $\langle [D'],[A] \rangle $ . Then we have ${\mathbb B}_+(D)\subset {\mathbb B}_{-}(D')$ .

Proof. By assumption, there exist positive real numbers $\lambda _{D'}$ and $\lambda _A$ , such that $D\equiv _{\mathbb {R}} \lambda _{D'} D' + \lambda _A A$ . By [8, Lemmas 1.8 and 1.14], we obtain:

$$\begin{align*}{\mathbb B}_{+}(D)={\mathbb B}_+(\lambda_{D'} D' + \lambda_A A) \subset {\mathbb B}_{-}(\lambda_{D'} D') = {\mathbb B}_{-}(D'), \end{align*}$$

which concludes the proof.

Lemma 2.3. Let M be a movable $\mathbb {R}$ -Cartier $\mathbb {R}$ -Weil divisor on a normal projective variety X. Then $[M]$ is contained in the interior of $\overline {\mathrm {Mov}}(X)$ if and only if ${\mathbb B}_{+}^1(M)=\emptyset $ .

Proof. Let A be an arbitrary ample divisor on X. By [8, Proposition 1.5], there exists $0<\epsilon \ll 1$ , such that ${\mathbb B}_{+}(M)={\mathbb B}(M-\epsilon ' A)$ for any $0<\epsilon '\leq \epsilon $ . In particular, it follows that ${\mathbb B}_{+}^1(M)=\emptyset $ if and only if ${\mathbb B}(M-\epsilon ' A)$ does not contain divisorial parts, that is, $M-\epsilon ' A$ is movable, which holds if and only if $[M]$ is contained in the interior of $\overline {\mathrm {Mov}}(X)$ .

2.B.2 Comparing base loci and $N_{\sigma }(D)$

Given a pseudoeffective $\mathbb {R}$ -Weil divisor D on a projective manifold X, the augmented and restricted base loci are closely related to the divisorial Zariski decomposition of D.

Lemma 2.4. Let D be a pseudoeffective $\mathbb {R}$ -Weil divisor on a projective manifold X. Then:

1. (1) $\operatorname *{\mathrm {Supp}}(N_{\sigma }(D))$ is precisely the divisor ${\mathbb B}_{-}^1(D)$ .

2. (2) If D is not movable and $[D]$ generates an extremal ray of $\overline {\mathrm {Eff}}(X)$ , then there exists a unique prime divisor $\Gamma \subset X$ , such that: $ [\Gamma ]\in \mathbb {R}_{>0} [D]. $ Moreover, we have:

   $$\begin{align*}\Gamma=\operatorname*{\mathrm{Supp}}(N_{\sigma}(D))={\mathbb B}_{-}^1(D). \end{align*}$$

Proof. Statement (1) follows from [38, V, Theorem 1.3], and statement (2) is proved in [15, Lemma 2.5]

As an immediate application, a pseudoeffective $\mathbb {R}$ -Weil divisor D on a projective manifold X is movable if and only if ${\mathbb B}_{-}^1(D)$ is empty (see also [38, III, Proposition 1.14].

Corollary 2.5. Given a projective manifold X, let D be a pseudoeffective $\mathbb {R}$ -Weil divisor and let M be a movable $\mathbb {R}$ -Weil divisor on X. Assume that:

1. (1) the divisor D is not movable and $[D]$ generates an extremal ray of $\overline {\mathrm {Eff}}(X)$ ;

2. (2) the divisor class $[M]$ is not contained in the interior of $\overline {\mathrm {Mov}}(X)$ and

3. (3) there exists an ample divisor A, such that $[M]$ is contained in the interior of the two-dimensional cone $\langle [D],[A]\rangle $ .

Then we have ${\mathbb B}_+^1(M)={\mathbb B}_{-}^1(D)=\operatorname *{\mathrm {Supp}}(N_{\sigma }(D))$ , which is the unique prime divisor contained in the ray $\mathbb {R}_{>0}[D]$ .

Proof. By our assumption (3) and Lemma 2.2, we have ${\mathbb B}_+(M)\subset {\mathbb B}_{-}(D)$ . As $[M]$ is not contained in the interior of $\overline {\mathrm {Mov}}(X)$ , it follows from Lemma 2.3 that ${\mathbb B}_+^1(M)$ is not empty. On the other hand, according to assumption (1) and Lemma 2.4, one obtains that ${\mathbb B}_-^1(D)=\operatorname *{\mathrm {Supp}}(N_{\sigma }(D))$ is the unique prime divisor which is contained in $\mathbb {R}_{>0}[D]$ . This forces that ${\mathbb B}_{+}^1(M)={\mathbb B}_{-}^1(D)$ .

2.C Positivity of vector bundles

Given a projective variety X, let E be a vector bundle of rank r over X. Denote by $\pi : \mathbb {P}(E)\rightarrow X$ the projectivised bundle in the sense of Grothendieck; that is,

$$\begin{align*}\mathbb{P}(E) := \mathrm{Proj}_X\left(\bigoplus_{r\geq 0} S^r E\right). \end{align*}$$

Denote by $\Lambda $ the tautological divisor of $\mathbb {P}(E)$ , that is, ${\mathcal O}_{\mathbb {P}(E)}(\Lambda )\cong {\mathcal O}_{\mathbb {P}(E)}(1)$ . We will use the following terminologies throughout this paper (see [29] for more details).

Definition 2.6. Let X be a projective variety.

1. (1) A $\mathbb {Q}$ -twisted vector bundle $E\hspace {-0.8ex}<\hspace {-0.8ex}\delta \hspace {-0.8ex}>$ on X is an ordered pair consisting of a vector bundle E on X, defined up to isomorphisms and a numerical equivalence $\mathbb {Q}$ -Cartier divisor class $\delta \in N^1(X)$ .

2. (2) The normalisation of a vector bundle E of rank r on X is the $\mathbb {Q}$ -twisted vector bundle:

   $$\begin{align*}E\hspace{-0.8ex}<\hspace{-0.8ex}-\frac{1}{r} c_1(E)\hspace{-0.8ex}>. \end{align*}$$

3. (3) A $\mathbb {Q}$ -twisted vector bundle $E\hspace {-0.8ex}<\hspace {-0.8ex}\delta \hspace {-0.8ex}>$ is said to be pseudoeffective (respectively, ample, big, nef) if the class $\Lambda +\pi ^*\delta $ is pseudoeffective (respectively, ample, big, nef) on $\mathbb {P}(E)$ .

4. (4) A $\mathbb {Q}$ -twisted vector bundle $E\hspace {-0.8ex}<\hspace {-0.8ex}\delta \hspace {-0.8ex}>$ is said almost nef if for a very general curve C, the restriction $E\hspace {-0.8ex}<\hspace {-0.8ex}\delta \hspace {-0.8ex}>|_C$ is nef. Here, very general curves mean that they intersect the complementary part of a countable union of proper subvarieties.

The following properties are well known for experts, and we include a complete proof for the reader’s convenience (see also [15, Lemmas 2.2 and 2.3]).

Proposition 2.7. Let X be a projective variety. Let E and F be vector bundles over X, and let $\delta \in N^1(X)$ be a $\mathbb {Q}$ -Cartier divisor class.

1. (1) The $\mathbb {Q}$ -twisted vector bundle $E\hspace {-0.8ex}<\hspace {-0.8ex}\delta \hspace {-0.8ex}>$ is pseudoeffective if and only if for an arbitrary big $\mathbb {Q}$ -Cartier $\mathbb {Q}$ -Weil divisor D on X and an arbitrary $\mathbb {Q}$ -Cartier $\mathbb {Q}$ -Weil divisor $\Delta $ on X, such that $[\Delta ]=\delta $ , there exists an effective $\mathbb {Q}$ -Weil divisor N satisfying:

   $$\begin{align*}N\sim_{\mathbb{Q}} \Lambda + \pi^*(\Delta + D). \end{align*}$$

2. (2) The $\mathbb {Q}$ -twisted vector bundle $E\hspace {-0.8ex}<\hspace {-0.8ex}\delta \hspace {-0.8ex}>$ is big if and only if the $\mathbb {Q}$ -twisted vector bundle $E\hspace {-0.8ex}<\hspace {-0.8ex}\delta -\gamma \hspace {-0.8ex}>$ is pseudoeffective for some big $\mathbb {Q}$ -Cartier class $\gamma \in \mathrm {Big}(X)$ .

Proof. One direction of statement (1) is clear since the pseudoeffective cone $\overline {\mathrm {Eff}}(\mathbb {P}(E))$ is closed. For the converse, we assume that $E\hspace {-0.8ex}<\hspace {-0.8ex}\delta \hspace {-0.8ex}>$ is pseudoeffective. Since D is big, by [28, Chapter 2, Corollary 2.2.7], there exists an ample $\mathbb {Q}$ -Cartier $\mathbb {Q}$ -Weil divisor A and an effective $\mathbb {Q}$ -Weil divisor $N'$ , such that $D \sim _{\mathbb {Q}} A + N'$ . On the other hand, as $\Lambda +\pi ^*\delta $ is $\pi $ -ample, there exists a rational number $0<\epsilon \ll 1$ , such that the $\mathbb {Q}$ -Cartier $\mathbb {Q}$ -Weil divisor $\epsilon (\Lambda +\pi ^*\Delta )+\pi ^*A$ is ample. This implies that:

$$\begin{align*}\Lambda+\pi^*(\Delta+D)\sim_{\mathbb{Q}} \epsilon(\Lambda+\pi^*\Delta)+\pi^*A + (1-\epsilon)(\Lambda+\pi^*\Delta)+N' \end{align*}$$

is big since $\mathrm {Big}(\mathbb {P}(E))$ is the interior of $\overline {\mathrm {Eff}}(\mathbb {P}(E))$ . Then it follows again from [28, Chapter 2, Corollary 2.2.7] that there exists an effective $\mathbb {Q}$ -Cartier $\mathbb {Q}$ -Weil divisor N, such that:

$$\begin{align*}N\sim_{\mathbb{Q}} \Lambda + \pi^* (\Delta + D). \end{align*}$$

One can easily obtain one implication of statement (2), since $\mathrm {Big}(\mathbb {P}(E))$ is open. Conversely, we assume that $E\hspace {-0.8ex}<\hspace {-0.8ex}\delta -\gamma \hspace {-0.8ex}>$ is pseudoeffective for some big $\mathbb {Q}$ -Cartier class $\gamma $ . Similar to the proof of statement (1), there exist a rational number $0<\epsilon \ll 1$ and an ample $\mathbb {Q}$ -Cartier $\mathbb {Q}$ -Weil divisor A and an effective $\mathbb {Q}$ -Weil divisor N such that the $\mathbb {Q}$ -Cartier divisor class $\epsilon (\Lambda +\pi ^*(\delta -\gamma ))+\pi ^*A$ is ample and:

$$\begin{align*}\Lambda+\pi^*\delta \equiv_{\mathbb{Q}} \epsilon(\Lambda+\pi^*(\delta-\gamma))+\pi^*A+(1-\epsilon)(\Lambda+\pi^*(\delta-\gamma)) + N. \end{align*}$$

Note that the $\mathbb {Q}$ -Cartier divisor class $(1-\epsilon )(\Lambda +\pi ^*(\delta -\gamma ))$ is pseudoeffective by our assumption. Then it is clear that the $\mathbb {Q}$ -Cartier divisor class $\Lambda +\pi ^*\delta $ is big.

We recall the following folklore result:

Lemma 2.8. Let X be a projective manifold of dimension n and H an ample divisor. Let E be an H-semistable vector bundle of rank r on X. Then the normalised vector bundle $E\hspace {-0.8ex}<\hspace {-0.8ex}-\frac {1}{r} c_1(E)\hspace {-0.8ex}>$ is not big.

Proof. Assume $E\langle -ac_1(E) \rangle $ is effective for some rational number $a>0$ ; that is, we have:

$$\begin{align*}H^0(X, \mathrm{Sym}^mE \otimes \det(E^*)^{\otimes (am)})\neq 0 \end{align*}$$

for some positive integer m, such that $am$ is an integer. This gives an injection:

$$\begin{align*}\det(E)^{\otimes (am)} \to \mathrm{Sym}^mE, \end{align*}$$

which yields:

$$\begin{align*}\mu_H^{\mathrm{max}} (\mathrm{Sym^m}E) \geq \mu_H (\det(E)^{\otimes (am)}) = am c_1(E) \cdot H^{n-1}. \end{align*}$$

On the other hand, as E is H-semistable, so is $\operatorname *{\mathrm {Sym}}^m E$ . Hence, we obtain:

$$\begin{align*}\mu_H^{\mathrm{max}} (\mathrm{Sym^m}E) = \mu_H (\mathrm{Sym^m} E) = \frac{m c_1(E)\cdot H^{n-1}}{r}, \end{align*}$$

which gives that $a \leq 1/r$ . In particular, it follows from Proposition 2.7 that $E\hspace {-0.8ex}<\hspace {-0.8ex}-\frac {1}{r} c_1(E)\hspace {-0.8ex}>$ is not big.

3 Fano manifolds with semiample tangent bundles

3.A Dual variety of VMRTs

Let X be a smooth projective variety of dimension n. Denote by $\operatorname *{\mathrm {RatCurves^n}}(X)$ the normalisation of the open subset of $\mathrm {Chow}(X)$ parameterising integral rational curves. By a family of rational curves in X, we mean an irreducible component ${\mathcal K}$ of $\operatorname *{\mathrm {RatCurves^n}}(X)$ . We denote by $\mathrm {Locus}({\mathcal K})$ the locus of X swept out by curves from ${\mathcal K}$ . We say that ${\mathcal K}$ is minimal if, for a general point $x\in \mathrm {Locus}({\mathcal K})$ , the closed subset ${\mathcal K}_x$ of ${\mathcal K}$ parameterising curves through x is proper. We say that ${\mathcal K}$ is dominating if $\mathrm {Locus}({\mathcal K})$ is dense in X. For an ample divisor H on X, we write $H \cdot {\mathcal K}$ the intersection number of H with a general curve parameterised by ${\mathcal K}$ .

3.A.1 Variety of minimal rational tangents

Every uniruled projective manifold X carries a dominating family of minimal rational curves. Fix one such family ${\mathcal K}$ . A general member $[C]\in {\mathcal K}$ is a standard rational curve, that is, if we denote by $f:\mathbb {P}^1\rightarrow C$ its normalisation, then there exists a nonnegative integer p, such that:

$$\begin{align*}f^*T_X \cong {\mathcal O}_{\mathbb{P}^1}(2)\oplus {\mathcal O}_{\mathbb{P}^1}(1)^{\oplus p} \oplus {\mathcal O}_{\mathbb{P}^1}^{\oplus (n-p-1)}. \end{align*}$$

Given a general point $x\in X$ , let ${\mathcal K}_x^n$ be the normalisation of ${\mathcal K}_x$ . Then ${\mathcal K}_x^n$ is a finite union of smooth projective varieties of dimension p. Define the tangent map $\tau _x:{\mathcal K}^n_x\dashrightarrow \mathbb {P}(\Omega _{X,x})$ by sending a curve that is smooth at x to its tangent direction at x. Define ${\mathcal C}_x$ to be the image of $\tau _x$ in $\mathbb {P}(\Omega _{X,x})$ . This is called VMRT at x associated to the minimal family ${\mathcal K}$ . The map $\tau _x:{\mathcal K}^n_x\dashrightarrow {\mathcal C}_x \subset \mathbb {P}(\Omega _{X,x})$ is in fact the normalisation morphism by [20, 25].

3.A.2 Dual variety

Let us recall the definition of dual varieties of projective varieties, and we refer the reader to [50] for more details. Let V be a complex vector space of dimension $N+1$ , and let $Z\subset \mathbb {P}^N=\mathbb {P}(V)$ be a projective variety. We denote by $T_{Z,z}$ the tangent space at any smooth point $z\in Z^{\text {sm}}$ , where $Z^{\text {sm}}$ is the nonsingular locus of Z. We denote by $\mathbf {T}_{Z,z}\subset \mathbb {P}^N$ the embedded projective tangent space of Z at z. A hyperplane $H\subset \mathbb {P}^N$ is a tangent hyperplane of Z if $\mathbf {T}_{Z,z}\subset H$ for some point $z\in Z^{\text {sm}}$ .

Definition 3.1. Let $Z\subset \mathbb {P}^N=\mathbb {P}(V)$ be a projective variety.

1. (1) The closure of the set of all tangent hyperplanes of Z is called the dual variety $\check {Z}\subset \check {\mathbb {P}}^N=\mathbb {P}(V^*)$ , where $V^*$ is the dual space of V.

2. (2) The dual defect $\mathrm {def}(Z)$ of Z is defined as $N-1-\dim (\check {Z})$ , and Z is called dual defective if $\mathrm { def}(Z)>0$ .

3. (3) The codegree $\operatorname *{\mathrm {codeg}}(Z)$ of Z is defined to be the degree of its dual variety $\check {Z}\subset \check {\mathbb {P}}^N$ .

3.A.3 Total dual variety of minimal rational tangents

Let C be a standard rational curve parameterised by ${\mathcal K}$ with normalisation $f:\mathbb {P}^1\rightarrow C$ . A minimal section of $\mathbb {P}(T_X)$ over the curve C is a section (denoted by $\bar {C}$ ) which corresponds to a quotient $f^*T_X\rightarrow {\mathcal O}_{\mathbb {P}^1}$ . Recall that $p=n-1$ if and only if X is isomorphic to $\mathbb {P}^n$ (cf. [7, 24]). In particular, if X is not isomorphic to projective spaces, such minimal sections always exist. Furthermore, we have $\Lambda \cdot \bar {C}=0$ for the tautological divisor $\Lambda $ on $\mathbb {P}(T_X)$ .

Definition 3.2. Let X be a uniruled projective manifold equipped with a dominating family ${\mathcal K}$ of minimal rational curves. The total dual variety of minimal rational tangents of ${\mathcal K}$ is defined as:

$$\begin{align*}\check{{\mathcal C}}:=\overline{\bigcup_{[C]\in {\mathcal K}:\ \text{standard} } \bar{C}}^{\text{Zar}} \subset \mathbb{P}(T_X), \end{align*}$$

where the union is taken over all minimal sections over all standard rational curves in ${\mathcal K}$ .

We remark that $\check {{\mathcal C}}$ is an irreducible projective variety. Moreover, for a general point $x\in X$ , let us denote by $\check {{\mathcal C}}_x$ the fibre of $\check {{\mathcal C}}\rightarrow X$ over x. The next result justifies the terminology in Definition 3.2:

Proposition 3.3 (37, Propositions 5.14 and 5.17)

Let X be an n-dimensional uniruled projective manifold equipped with a dominating family ${\mathcal K}$ of minimal rational curves and $x \in X$ a general point. Then $\check {\mathcal {C}}_x$ is the dual variety of $\mathcal {C}_x$ .

Moreover, let c be the dual defect of ${\mathcal C}_x\subset \mathbb {P}(\Omega _{X,x})$ . Then for a minimal section $\bar {C}$ over a general standard rational curve $[C]\in {\mathcal K}_x$ with normalisation $\bar {f}: \mathbb {P}^1 \rightarrow \bar {C}$ , we have:

$$\begin{align*}\bar{f}^*T_{\mathbb{P}(T_X)}\cong {\mathcal O}_{\mathbb{P}^1}(-2)\oplus{\mathcal O}_{\mathbb{P}^1}(2)\oplus{\mathcal O}_{\mathbb{P}^1}(-1)^{\oplus c}\oplus{\mathcal O}_{\mathbb{P}^1}(1)^{\oplus c}\oplus{\mathcal O}_{\mathbb{P}^1}^{\oplus (2n-2c-3)}. \end{align*}$$

As an immediate corollary of Proposition 3.3, the dual variety of the VMRT ${\mathcal C}_x$ at a general point x is always pure dimensional. Moreover, the total dual VMRT $\check {{\mathcal C}}$ is a prime divisor in $\mathbb {P}(T_X)$ if and only if $\check {{\mathcal C}}_x\subset \mathbb {P}(T_{X,x})$ at a general point $x\in X$ is a (possibly reducible) hypersurface, that is, ${\mathcal C}_x\subset \mathbb {P}(\Omega _{X,x})$ is not dual defective.

The importance of the total dual VMRT in the study of positivity of tangent bundles is illustrated in the following theorem (see also [14, 15, 37, 41].

Theorem 3.4. Let X be a Fano manifold of Picard number $1$ equipped with a dominating family ${\mathcal K}$ of minimal rational curves. Let H be the ample generator of $\operatorname *{\mathrm {Pic}}(X)$ , and let $\Lambda $ be the tautological divisor of $\pi :\mathbb {P}(T_X)\rightarrow X$ . Assume that the VMRT ${\mathcal C}_x\subset \mathbb {P}(\Omega _{X,x})$ at a general point $x\in X$ is not dual defective. Denote by a and b the unique integers, such that:

$$\begin{align*}[\check{{\mathcal C}}] \equiv a\Lambda - b\pi^*H. \end{align*}$$

Then a is equal to the codegree of ${\mathcal C}_x$ and the following statements hold.

1. (1) $T_X$ is big if and only if $b>0$ .

2. (2) If $T_X$ is big, then $bH\cdot {\mathcal K}\leq 2$ with equality if and only if there exists a minimal section $\bar {C}$ over a general standard rational curve $[C]\in {\mathcal K}$ , such that $\check {{\mathcal C}}$ is smooth along $\bar {C}$ .

3. (3) If $T_X$ is big, then $[\check {{\mathcal C}}]$ generates an extremal ray of $\overline {\mathrm {Eff}}(\mathbb {P}(T_X))$ ; that is, we have:

   $$\begin{align*}\overline{\mathrm{Eff}}(\mathbb{P}(T_X))=\langle [\check{{\mathcal C}}], [\pi^*H]\rangle. \end{align*}$$

Proof. By our assumption, the projective variety $\check {{\mathcal C}}_x\subset \mathbb {P}(T_{X,x})$ is a (possibly reducible) hypersurface of degree $\operatorname *{\mathrm {codeg}}({\mathcal C}_x)$ . On the other hand, we have:

$$\begin{align*}[\check{{\mathcal C}}]|_{\mathbb{P}(T_{X,x})} \equiv (a\Lambda-b\pi^*H)|_{\mathbb{P}(T_{X,x})}\equiv c_1\left({\mathcal O}_{\mathbb{P}(T_{X,x})}(a)\right). \end{align*}$$

This implies that a is equal to the codegree of ${\mathcal C}_x$ .

Proof of (1). Note that if $b>0$ , then it follows from Proposition 2.7 that $T_X$ is big. Now we assume that $T_X$ is big. Denote by $\alpha _X:=\alpha (X,H)$ the pseudoeffective threshold of X, namely, the maximal positive real number, such that $\Lambda -\alpha _X \pi ^*H$ is pseudoeffective. Note that $\check {{\mathcal C}}$ is dominated by minimal sections $\bar {C}$ over standard rational curves in ${\mathcal K}$ , and we have:

$$\begin{align*}(\Lambda-\alpha_X \pi^*H) \cdot \bar{C}=-\alpha_X H\cdot C<0. \end{align*}$$

Therefore, the restriction $(\Lambda -\alpha _X \pi ^*H)|_{\check {{\mathcal C}}}$ is not pseudoeffective. In particular, the $\mathbb {R}$ -divisor $\Lambda -\alpha _X \pi ^*H$ is not movable and the total dual VMRT $\check {{\mathcal C}}$ is contained in the effective Weil divisor:

$$\begin{align*}\Gamma:=\operatorname*{\mathrm{Supp}}(N_{\sigma}(\Lambda-\alpha_X \pi^*H))={\mathbb B}_{-}^1(\Lambda-\alpha_X \pi^*H). \end{align*}$$

As X has Picard number $1$ , it follows that $\rho (\mathbb {P}(T_X))=2$ and $R=\mathbb {R}_{\geq 0}[\Lambda -\alpha _X \pi ^*H]$ is an extremal ray of $\overline {\mathrm {Eff}}(\mathbb {P}(T_X))$ . Then it follows from Lemma 2.4 that $\Gamma $ is a prime divisor generating the extremal ray R. This yields that $\Gamma =\check {{\mathcal C}}$ , and, hence, $b>0$ .

Proof of (2). Let $\bar {C}$ be a minimal section over a general standard rational curve C in ${\mathcal K}$ with normalisation $\bar {f}:\mathbb {P}^1\rightarrow \bar {C}$ . As ${\mathcal C}_x$ is not dual defective, by Proposition 3.3, we have:

(3.1) $$ \begin{align} \bar{f}^*T_{\mathbb{P}(T_X)} \cong {\mathcal O}_{\mathbb{P}^1}(-2)\oplus {\mathcal O}_{\mathbb{P}^1}(2)\oplus {\mathcal O}_{\mathbb{P}^1}^{\oplus (2n-3)}. \end{align} $$

Moreover, by the generic choice of C, we may assume that $\bar {C}$ is not contained in the singular locus of $\check {{\mathcal C}}$ . Then we have the following exact sequence of sheaves:

$$\begin{align*}{\mathcal N}^*_{\check{{\mathcal C}}/\mathbb{P}(T_X)}\longrightarrow \Omega_{\mathbb{P}(T_X)}|_{\check{{\mathcal C}}}\longrightarrow \Omega_{\check{{\mathcal C}}} \longrightarrow 0, \end{align*}$$

where ${\mathcal N}^*_{\check {{\mathcal C}}/\mathbb {P}(T_X)}$ is the conormal sheaf of $\check {{\mathcal C}}$ in $\mathbb {P}(T_X)$ . In particular, since $\check {{\mathcal C}}$ is a Cartier divisor in $\mathbb {P}(T_X)$ , we have:

$$\begin{align*}{\mathcal N}^*_{\check{{\mathcal C}}/\mathbb{P}(T_X)}={\mathcal O}_{\mathbb{P}(T_X)}(-\check{{\mathcal C}})|_{\check{{\mathcal C}}}={\mathcal O}_{\mathbb{P}(T_X)}(-a\Lambda+b\pi^*H)|_{\check{{\mathcal C}}}. \end{align*}$$

Consequently, the conormal sheaf is invertible. Pulling back the exact sequence by $\bar {f}$ yields an exact sequence:

Note that the map $\iota $ is generically injective since $\bar {C}$ is not contained in the singular locus of $\check {{\mathcal C}}$ . As $b>0$ , it follows from (3.1) that $bH\cdot C\leq 2$ with equality if and only if $\iota $ is an injection of vector bundles, that is, $\bar {f}^*\Omega _{\check {{\mathcal C}}}$ is locally free. By Nakayama’s lemma, the latter one is equivalent to the smoothness of $\check {{\mathcal C}}$ along $\bar {C}$ . Conversely, if $\check {{\mathcal C}}$ is smooth along $\bar {C}$ , then $\iota $ is an injection of vector bundles. In particular, as $b>0$ , we obtain $bH\cdot C=2$ by (3.1).

Proof of (3). Since $T_X$ is big and X has Picard number $1$ , we have:

$$\begin{align*}\overline{\mathrm{Eff}}(\mathbb{P}(T_X))=\langle [\Lambda - \alpha_X\pi^*H],[\pi^*H]\rangle. \end{align*}$$

On the other hand, note that $\check {{\mathcal C}}$ is dominated by curves with $\Lambda $ -degree $0$ , it follows that the restriction $(\Lambda -\alpha _X\pi ^*H)|_{\check {{\mathcal C}}}$ is not pseudoeffective. In particular, the $\mathbb {R}$ -divisor $\Lambda - \alpha _X \pi ^*H$ is not movable and $\check {{\mathcal C}}$ is contained in $\operatorname *{\mathrm {Supp}}(N_{\sigma }(\Lambda -\alpha _X \pi ^*H))$ . Then it follows from Lemma 2.4 that $\check {{\mathcal C}}=\operatorname *{\mathrm {Supp}}(N_{\sigma }(\Lambda -\alpha _X \pi ^*H))$ and $[\check {{\mathcal C}}]$ is contained in the ray $\mathbb {R}_{>0}[\Lambda -\alpha _X\pi ^*H]$ .

Corollary 3.5. Let C be a nonsingular projective curve of genus $\geq 4$ . Let $X:=\mathrm {SU}_C(r,d)$ be the moduli space of stable vector bundles of rank r with fixed determinant of degree d. Assume that r and d are coprime. If $r\geq 3$ , then $T_X$ is not big.

Proof. It is known that X is a nonsingular Fano manifold of Picard number $1$ , such that $-K_X=2H$ , where H is the ample generator of $\operatorname *{\mathrm {Pic}}(X)$ . On the other hand, there exists a dominating family ${\mathcal K}$ of minimal rational curves on X given by the so-called Hecke curves, such that $-K_X\cdot {\mathcal K}=2r$ [22, § 3]. By [22, Theorem 4.4], the total dual VMRT $\check {{\mathcal C}}$ is a divisor in $\mathbb {P}(T_X)$ . Then Theorem 3.4 implies that $T_X$ is not big as $H\cdot {\mathcal K}=r\geq 3$ .

Remark 3.6. If C is a nonsingular projective curve of genus $g=2$ , then the moduli space $X:=\mathrm {SU}_C(2,r)$ with r odd is isomorphic to the intersection of two quadrics in $\mathbb {P}^5$ , and it is shown in [15, Theorem 1.5] that $T_X$ is pseudoeffective but not big.

3.B Semiample tangent bundles

We consider in this subsection Fano manifolds with big and nef tangent bundles. It is conjectured by Campana-Peternell in [5] that a Fano manifold with nef tangent bundle must be a rational homogeneous space. Conversely, it is also known that the tangent bundle of a rational homogeneous space is big and globally generated. Recall that a vector bundle E over a projective variety is said to be semiample if ${\mathcal O}_{\mathbb {P}(E)}(1)$ is semiample.

Lemma 3.7. Let X be an n-dimensional projective manifold, such that $T_X$ is big and nef.

1. (1) The tangent bundle $T_X$ is semiample.

2. (2) The projectivised tangent bundle $\mathbb {P}(T_X)$ is a Mori dream space.

Proof. As $T_X$ is big and nef, $\mathbb {P}(T_X)$ is a weak Fano manifold, that is, $-K_{\mathbb {P}(T_X)}$ is big and nef. Then statement (1) follows from the base-point-free theorem, and statement (2) follows from [3, Corollary 1.3.2] since a weak Fano manifold is always log Fano.

We refer the reader to [17] for the definition of Mori dream spaces and their basic properties.

Definition 3.8. Let X be a $\mathbb {Q}$ -factorial normal projective variety. A small $\mathbb {Q}$ -factorial modification (SQM for short) of X is a birational map $g: X \dashrightarrow X'$ , where $X'$ is a $\mathbb {Q}$ -factorial normal projective variety and g is an isomorphism in codimension $1$ .

Throughout the rest of this subsection, we will always assume that X is a Fano manifold of Picard number $1$ , such that $T_X$ is big and nef. Let us denote by H the ample generator of $\operatorname *{\mathrm {Pic}}(X)$ and by $\Lambda $ the tautological divisor of $\mathbb {P}(T_X)$ . Then the evaluation of global sections defines a birational morphism:

(3.2)

The morphism $\varepsilon $ is an isomorphism if and only if $T_X$ is ample, and Mori proved in [35] that the tangent bundle of a projective manifold X is ample if and only if X is isomorphic to a projective space. For projective spaces, we have the following description of the cones of divisors.

Example 3.9. Let X be the n-dimensional projective space $\mathbb {P}^n$ with $n\geq 2$ , and let $\Lambda $ be the tautological divisor class of $\pi :\mathbb {P}(T_{X})\rightarrow X$ . Then we have:

$$ \begin{align*} \overline{\mathrm{Eff}}(\mathbb{P}(T_{\mathbb{P}^n})) = \mathrm{Eff} (\mathbb{P}(T_{\mathbb{P}^n}) ) = \mathrm{Nef} (\mathbb{P} (T_{\mathbb{P}^n}))=\left\langle [\Lambda -\pi^*H], [\pi^*H]\right\rangle, \end{align*} $$

where H is a hyperplane section of $\mathbb {P}^n$ . Indeed, we consider the following Euler sequence:

$$\begin{align*}0\longrightarrow {\mathcal O}_{\mathbb{P}^n} \longrightarrow {\mathcal O}_{\mathbb{P}^n}(1)^{\oplus (n+1)} \longrightarrow T_{\mathbb{P}^n} \longrightarrow 0. \end{align*}$$

It follows that $T_{\mathbb {P}^n}(-1)$ is globally generated. In particular, the divisor class $[\Lambda -\pi ^*H]$ is contained in the intersection $\mathrm {Eff}(\mathbb {P}(T_X))\cap \mathrm {Nef}(\mathbb {P}(T_X))$ . On the other hand, it is known that $\Lambda -\pi ^*H$ is not big, and, hence, $[\Lambda -\pi ^*H]$ is not contained in the interior of $\mathrm {Eff}(\mathbb {P}(T_X))$ .

Let us collect some basic properties about the morphism $\varepsilon $ .

Proposition 3.10. Let X be a Fano manifold of Picard number $1$ , such that $T_X$ is big and nef. Denote by $\varepsilon :{\mathcal X}\rightarrow {\mathcal Y}$ the birational morphism given in (3.2). If $\varepsilon $ is a divisorial contraction, then the following statements hold.

1. (1) The projective variety ${\mathcal Y}$ has at worst $\mathbb {Q}$ -factorial canonical singularities.

2. (2) The exceptional locus of $\varepsilon $ is an irreducible divisor $\Gamma $ , such that the general fibre of $\Gamma \rightarrow \varepsilon (\Gamma )$ consists of either a smooth $\mathbb {P}^1$ or the union of two $\mathbb {P}^1$ ’s meeting at a point.

3. (3) Let F be an irreducible component of a general one-dimensional fibre of $\varepsilon $ . Then there exists a nonnegative integer a, such that:

   $$\begin{align*}T_{{\mathcal X}}|_{F}\cong {\mathcal O}_{\mathbb{P}^1}(2)\oplus {\mathcal O}_{\mathbb{P}^1}(-2)\oplus {\mathcal O}_{\mathbb{P}^1}(1)^{\oplus a} \oplus {\mathcal O}_{\mathbb{P}^1}(-1)^{\oplus a}\oplus {\mathcal O}_{\mathbb{P}^1}^{\oplus 2n-2a-3}. \end{align*}$$

Proof. Claims (1) and (2) follow from [37, Proposition 5.10] and [52, Theorem 1.3]. To prove (3), we follow the argument of [52, Proposition 2.13]. Let:

$$\begin{align*}0\rightarrow E\rightarrow T_{{\mathcal X}}\rightarrow {\mathcal O}_{{\mathcal X}}(1)\rightarrow 0 \end{align*}$$

be the natural contact structure on ${\mathcal X}$ . By our assumption, we have ${\mathcal O}_{{\mathcal X}}(1)|_F\cong {\mathcal O}_F$ . Then the contact structure induces a natural isomorphism $E|_F\cong E^*|_F$ . Let:

$$\begin{align*}E|_F\cong \bigoplus_{i=1}^{2n-2} {\mathcal O}_{\mathbb{P}^1}(a_i) \end{align*}$$

be the decomposition with $a_1\geq \cdots \geq a_{2n-2}$ . Since the problem is local in ${\mathcal Y}$ , after removing a subvariety of codimension at least $4$ of ${\mathcal Y}$ , we may assume that all fibres of $\varepsilon $ are at most one dimensional. Then the argument of [52, Proposition 2.13] applies verbatim to our situation to obtain $h^1(F,\Omega _X|_F)=1$ and the short exact sequence below:

(3.3) $$ \begin{align} 0\longrightarrow {\mathcal O}_F \longrightarrow \Omega_X|_F \longrightarrow E^*|_F=E|_F\longrightarrow 0 \end{align} $$

implies $h^1(F,E|_F)=1$ . This implies that $a_{2n-2}=-2$ and $a_{2n-3}\geq -1$ . The isomorphism $E|_F\cong E^*|_F$ shows that $E|_F$ must be of the form:

$$\begin{align*}{\mathcal O}_{\mathbb{P}^1}(2)\oplus {\mathcal O}_{\mathbb{P}^1}(1)^{\oplus a} \oplus {\mathcal O}_{\mathbb{P}^1}^{\oplus 2n-2a-4} \oplus {\mathcal O}_{\mathbb{P}^1}(-1)^{\oplus a} \oplus {\mathcal O}_{\mathbb{P}^1}(-2). \end{align*}$$

Then it follows from (3.3) and the fact $h^1(E|_F)=h^1(E^*|_F)=1$ that $T_X|_F$ is either of the form $E\oplus {\mathcal O}_{\mathbb {P}^1}$ or of the form:

$$\begin{align*}{\mathcal O}_{\mathbb{P}^1}(2)\oplus {\mathcal O}_{\mathbb{P}^1}(1)^{\oplus a} \oplus {\mathcal O}_{\mathbb{P}^1}^{\oplus 2n-2a-4} \oplus {\mathcal O}_{\mathbb{P}^1}(-1)^{\oplus a+2}. \end{align*}$$

It is clear that the $\mathrm {Chow}({\mathcal X})$ has dimension $\geq 2n-3$ at $[F]$ as $\Gamma $ has dimension $2n-2$ and the deformation of F dominates $\Gamma $ . Hence, we have $h^0(F,T_{{\mathcal X}}|_F)\geq 2n$ and $T_X|_F$ is of the form $E\oplus {\mathcal O}_{\mathbb {P}^1}$ .

Definition 3.11. Let X be a Fano manifold of Picard number $1$ , such that $T_X$ is big and nef. Denote by $\varepsilon :{\mathcal X}\rightarrow {\mathcal Y}$ the birational morphism given in (3.2). The projective variety ${\mathcal Y}$ is of type $A_1$ (respectively, $A_2$ ) if the morphism $\varepsilon $ is a divisorial contraction and the general fibre of $E\rightarrow \varepsilon (E)$ is a smooth $\mathbb {P}^1$ (respectively, union of two $\mathbb {P}^1$ ’s meeting in a point).

In the sequel of this subsection, we will focus on the description of the cones of divisors of ${\mathcal X}$ . Similar to the pseudoeffective threshold $\alpha _X:=\alpha (X,H)$ , we define the movable threshold $\beta _X:=\beta (X,H)$ to be the maximal real number, such that the $\mathbb {R}$ -divisor $\Lambda -\beta _X \pi ^*H$ is movable. Clearly, we have $\alpha _X \geq \beta _X$ . Since $\Lambda $ is big, by Proposition 2.7, we obtain $\alpha _X>0$ . Moreover, as $\Lambda $ is semiample, we also have $\beta _X\geq 0$ .

Given a Weil divisor $\Gamma \subset {\mathcal X}$ , let us denote by $a(\Gamma )$ and $b(\Gamma )$ the unique integers, such that:

$$\begin{align*}\Gamma\equiv a(\Gamma)\Lambda - b(\Gamma)\pi^*H. \end{align*}$$

First, we have the following general observation.

Proposition 3.12. Let X be an n-dimensional Fano manifold of Picard number $1$ , such that $T_X$ is big and nef.

1. (1) Both $\alpha _X$ and $\beta _X$ are rational numbers, and there exists a SQM $g:{\mathcal X}'\dashrightarrow {\mathcal X}$ , such that the $\mathbb {Q}$ -Cartier $\mathbb {Q}$ -Weil divisor $g^*(\Lambda -\beta _X\pi ^*H)$ is semiample.

2. (2) If $\alpha _X\not =\beta _X$ , then there exists a unique prime divisor $\Gamma \subset {\mathcal X}$ , such that:

   $$ \begin{align*} [\Gamma]\in \mathbb{R}_{>0}[\Lambda-\alpha_X\pi^*H]\quad \text{and}\quad g^*\Gamma \cdot \left(g^*(\Lambda-\beta_X\pi^*H)\right)^{2n-2}=0, \end{align*} $$
   where $g:{\mathcal X}'\dashrightarrow {\mathcal X}$ is the SQM provided in statement (1).

Proof. Recall that ${\mathcal X}$ is a Mori dream space by Lemma 3.7. By [17, Proposition 1.11], there exists a SQM , such that:

$$\begin{align*}[g^*(\Lambda-\beta_X\pi^*H)]\in \mathrm{Nef}({\mathcal X}'). \end{align*}$$

Moreover, as ${\mathcal X}'$ is again a Mori dream space, it follows that $\mathrm {Nef}({\mathcal X}')$ is generated by semiample $\mathbb {Q}$ -Cartier divisors. Hence, $\beta _X$ is a rational number.

Now assume that $\alpha _X\not =\beta _X$ . Then $\Lambda -\alpha _X\pi ^*H$ is not movable. Moreover, as X has Picard number $1$ , it is clear that $R=\mathbb {R}_{>0}[\Lambda -\alpha _X\pi ^*H]$ is an extremal ray of $\overline {\mathrm {Eff}}({\mathcal X})$ . Then, by Lemma 2.4, there exists a unique prime divisor $\Gamma \subset {\mathcal X}$ , such that $[\Gamma ]\in \mathbb {R}_{>0}[\Lambda -\alpha _X \pi ^*H]$ . In particular, we have:

$$\begin{align*}\alpha_X=\frac{b(\Gamma)}{a(\Gamma),} \end{align*}$$

and, hence, $\alpha _X$ is again a rational number. Denote by $\Gamma '$ the divisor $g^*\Gamma $ . Note that the pseudoeffective cones and movables are preserved by $g^*$ . In particular, by Lemma 2.2, we obtain:

$$\begin{align*}{\mathbb B}_+^1(g^*(\Lambda - \beta_X\pi^*H))\subset {\mathbb B}_{-}^1(\Gamma')\subset \Gamma'. \end{align*}$$

Since $\Lambda -\beta _X \pi ^*H$ is not contained in the interior of $\overline {\mathrm {Mov}}({\mathcal X})$ , so is the pull-back $g^*(\Lambda -\beta _X\pi ^*H)$ . In particular, by Lemma 2.3, we have:

$$\begin{align*}{\mathbb B}_+^1(g^*(\Lambda - \beta_X \pi^*H))=\Gamma'. \end{align*}$$

On the other hand, as $g^*(\Lambda -\beta _X\pi ^*H)$ is nef, by [2, Theorem 1.4], $\Gamma '$ is contained in the null locus of $g^*(\Lambda -\beta _X\pi ^*H)$ . In particular, we obtain:

$$\begin{align*}g^*\Gamma \cdot \left(g^*(\Lambda-\beta_X\pi^*H)\right)^{2n-2} = \Gamma'\cdot \left(g^*(\Lambda-\beta_X\pi^*H)\right)^{2n-2} = 0. \end{align*}$$

This completes the proof.

According to Proposition 3.12, the calculation of the cones of divisors of ${\mathcal X}$ is very closely related to the study of possible SQMs of ${\mathcal X}$ , which in general seems to be a very difficult problem. However, if we assume that the morphism $\varepsilon :{\mathcal X}\rightarrow {\mathcal Y}$ is a divisorial contraction, then the cones of divisors of ${\mathcal X}$ can be explicitly determined.

Proposition 3.13. Let X be an n-dimensional Fano manifold of Picard number $1$ , such that $T_X$ is big and nef and the VMRT of X at a general point is smooth. Assume that the evaluation morphism $\varepsilon :{\mathcal X}\rightarrow {\mathcal Y}$ is a divisorial contraction with exceptional divisor $\Gamma $ . Let F be an irreducible component of a general fibre of $\Gamma \rightarrow \varepsilon (\Gamma )$ . Then we have:

1. (1) $\beta _X=0$ , ${\mathbb B}_{+}(\Lambda )=\Gamma $ and $[\Gamma ]$ generates the extremal ray $ \mathbb {R}_{>0}[\Lambda -\alpha _X\pi ^*H]$ . In particular, we have $\Gamma \cdot \Lambda ^{2n-2}=0$ .

2. (2) $b(\Gamma )\leq 2$ with equality if and only if ${\mathcal Y}$ is of type $A_1$ and there exists a dominating family ${\mathcal K}$ of minimal rational curves on X, such that $\check {{\mathcal C}}=\Gamma $ and $H\cdot {\mathcal K}=1$ .

Proof. Since $\Lambda $ is big and nef, it follows from [2, Theorem 1.4] that ${\mathbb B}_{+}(\Lambda )$ coincides with the exceptional locus $\Gamma $ of $\varepsilon $ . In particular, $\Gamma \cdot \Lambda ^{2n-2}=(\Lambda |_{\Gamma })^{2n-2} = 0$ . Moreover, according to Lemma 2.3, $[\Lambda ]$ is not contained in the interior of $\overline {\mathrm {Mov}}({\mathcal X})$ . This implies $\beta _X=0$ . Then it follows from Corollary 2.5 that $[\Gamma ]\in \mathbb {R}_{>0}[\Lambda -\alpha _X\pi ^*H]$ . Combining Proposition 3.10 with the same argument as in the proof of Theorem 3.4(3) shows that $b(\Gamma )\pi ^*H\cdot F\leq 2$ with equality if and only if $\Gamma $ is smooth along F. Then we obtain that $b(\Gamma )\leq 2$ with equality if and only if $\Gamma $ is smooth along F and $\pi ^*H\cdot F=1$ . Now the result follows from the following two claims.

Claim 1. $\Gamma $ is smooth along F if and only if ${\mathcal Y}$ is of type $A_1$ .

Proof of Claim 1

First, we assume that $\Gamma $ is smooth along F, then the nonsingular locus $\Gamma ^{\text {sm}}$ contains F. In particular, by generic smoothness and the generic choice of F, it follows that the fibre of $\Gamma ^{\text {sm}}\rightarrow \varepsilon (\Gamma ^{\text {sm}})$ over $\varepsilon (F)$ is smooth. Nevertheless, if the fibre of $\varepsilon $ over $\varepsilon (F)$ consists of another irreducible component $F'$ , such that F and $F'$ are meeting at a point x, then we have $x\in \Gamma ^{\text {sm}}$ , and, therefore, $F'\cap \Gamma ^{\text {sm}}$ is not empty. In particular, the fibre of $\Gamma ^{\text {sm}}\rightarrow \varepsilon (\Gamma ^{\text {sm}})$ over $\varepsilon (F)$ is not smooth, a contradiction. Hence, ${\mathcal Y}$ is of type $A_1$ .

Conversely, if ${\mathcal Y}$ is of type $A_1$ , then $\Gamma \rightarrow \varepsilon (\Gamma )$ is a smooth $\mathbb {P}^1$ -fibration over a Zariski open subset of $\varepsilon (\Gamma )$ . In particular, the singular locus of $\Gamma $ does not dominate $\varepsilon (\Gamma )$ , and, hence, $\Gamma $ is smooth along F as F is a general fibre.

Claim 2. $\pi ^*H\cdot F=1$ if and only if there exists a dominating family ${\mathcal K}$ of minimal rational curves over X, such that $H\cdot {\mathcal K}=1$ and $\check {{\mathcal C}}=\Gamma $ .

Proof of Claim 2

First, we assume that $\pi ^*H\cdot F=1$ . Then the induced morphism $F\rightarrow \pi (F)$ is birational and $H\cdot F=1$ . In particular, the images of the irreducible components of general fibres of $\Gamma \rightarrow \varepsilon (\Gamma )$ in X form a dominating family ${\mathcal K}$ of rational curves, such that $H\cdot {\mathcal K}=1$ . Therefore, ${\mathcal K}$ is actually a dominating family of minimal rational curves. Let $\check {{\mathcal C}}$ be the total dual VMRT of ${\mathcal K}$ . As $\check {{\mathcal C}}$ is dominated by curves with $\Lambda $ -degree $0$ , it follows that $\check {{\mathcal C}}\subset \Gamma $ . On the other hand, as the VMRT of X at a general point is smooth, every rational curve parameterised by ${\mathcal K}$ passing through a general point is standard (cf. [18, Proposition 1.4]). In particular, by generic choice of F, we may assume that $\pi (F)$ is a standard rational curve parameterised by ${\mathcal K}$ . In particular, the curve F is a minimal section over $\pi (F)$ . It follows that $\Gamma \subset \check {{\mathcal C}}$ , and, hence, $\Gamma =\check {{\mathcal C}}$ .

Conversely, assume that there exists a dominating family ${\mathcal K}$ of minimal rational curves on X, such that $H\cdot {\mathcal K}=1$ and $\check {{\mathcal C}}=\Gamma $ . As $\check {{\mathcal C}}$ is dominated by minimal sections $\bar {C}$ over standard rational curves C in ${\mathcal K}$ , it follows that $\bar {C}$ is contained in a general fibre of $\Gamma \rightarrow \varepsilon (\Gamma )$ . In particular, we have $\pi ^*H\cdot \bar {C}=H\cdot C=1$ . By the generic choice of F, the curve F is actually a minimal section over some standard rational curve in ${\mathcal K}$ , and, hence, $\pi ^*H\cdot F=1$ .

Remark 3.14. In the setting of Proposition 3.13, to explicitly determine the pseudoeffective cone $\overline {\mathrm { Eff}}({\mathcal X})$ , it is enough to calculate the cohomological class of $\Gamma $ in $\operatorname *{\mathrm {Pic}}({\mathcal X})$ , that is, determining $a(\Gamma )$ and $b(\Gamma )$ . Statement (2) gives a totally geometric method to determine $b(\Gamma )$ . Then one can use the equality $\Gamma \cdot \Lambda ^{2n-2}=0$ in statement (1) to obtain the rational number $b(\Gamma )/a(\Gamma )$ , and finally we get the precise value of $a(\Gamma )$ . On the other hand, if there exists a dominating family ${\mathcal K}$ of minimal rational curves on X, such that $\check {{\mathcal C}}$ is a divisor, then we must have $\check {{\mathcal C}}=\Gamma $ , and we can also apply Theorem 3.4 to calculate $a(\Gamma )$ . In a later section, we will apply these results to rational homogeneous spaces.

4 Varieties of small codegree and Proof of Theorem 1.9

4.A Segre inequality

Let us recall the following Segre inequality, which gives a sharp lower bound for the codegree of an irreducible and linearly nondegenerate projective variety in terms of its dimension and codimension.

Theorem 4.1 (46)

Let $Z\subsetneq \mathbb {P}^N$ be an n-dimensional irreducible and linearly nondegenerate projective variety. Assume that the dual variety $\check {Z}\subset \check {\mathbb {P}}^N$ is a hypersurface with nonvanishing hessian. Then we have:

(4.1) $$ \begin{align} \operatorname*{\mathrm{codeg}}(Z):=\deg(\check{Z})\geq \frac{2(N+1)}{n+2}. \end{align} $$

Moreover, the equality holds if and only if $\check {Z}\subset \check {\mathbb {P}}^N$ is a hypersurface defined by $F=0$ , such that its hessian $h_F$ satisfies $h_F = F^{N-n-1}$ .

Remark 4.2. Zak kindly informed us that the Segre inequality may fail if the dual variety $\check {Z}$ is a hypersurface with vanishing hessian. There are very few known examples of smooth projective varieties whose dual variety is a hypersurface with vanishing hessian. Gondim, Russo and Staglianò proved in [12, Corollary 4.5] that the projection from an internal point of $\nu _2(\mathbb {P}^n)\subset \mathbb {P}^{\frac {n^2+3n}{2}}$ is a smooth variety $Z\subset \mathbb {P}^{\frac {n^2+3n-2}{2}}$ , such that the dual variety $\check {Z}$ is a degree $n+1$ hypersurface with vanishing hessian. It would be very interesting to find more examples.

It is somewhat surprising that there exists a link between Conjectures 1.6 and 1.2, which is bridged by the following simple observation:

Proposition 4.3. Let X be an n-dimensional Fano manifold of Picard number $1$ equipped with a dominating family ${\mathcal K}$ of minimal rational curves. If the normalised tangent bundle of X is pseudoeffective and the VMRT ${\mathcal C}_x\subset \mathbb {P}(\Omega _{X,x})$ at a general point is not dual defective, then we have:

(4.2) $$ \begin{align} \operatorname*{\mathrm{codeg}}({\mathcal C}_x)\leq \frac{2\dim(X)}{\dim({\mathcal C}_x)+2}. \end{align} $$

Proof. Let H be the ample generator of $\operatorname *{\mathrm {Pic}}(X)$ and denote by $\alpha _X:=\alpha (X,H)$ the pseudoeffective threshold of X with respect to H. Let $i_X$ be the index of X, that is, $-K_X=i_XH$ . Then the normalised tangent bundle of X is pseudoeffective if and only if the following inequality holds:

$$\begin{align*}\alpha_X\geq \frac{i_X}{\dim(X)}. \end{align*}$$

On the other hand, since ${\mathcal C}_x$ is not dual defective, the total dual VMRT $\check {{\mathcal C}}\subset \mathbb {P}(T_X)$ is a prime divisor. Write $[\check {{\mathcal C}}]\equiv a \Lambda - b\pi ^*H$ . Then, by Theorem 3.4, we obtain:

$$\begin{align*}a=\operatorname*{\mathrm{codeg}}({\mathcal C}_x),\quad 0<bH\cdot {\mathcal K}\leq 2 \quad \text{and} \quad \alpha_X=\frac{b}{a}. \end{align*}$$

Therefore we get:

$$\begin{align*}\frac{2}{\operatorname*{\mathrm{codeg}}({\mathcal C}_x)}\geq \alpha_X H\cdot {\mathcal K} \geq \frac{i_X H\cdot {\mathcal K}}{\dim(X)}=\frac{\dim({\mathcal C}_x)+2}{\dim(X)}, \end{align*}$$

and the result follows. Here, we use the fact that $\dim ({\mathcal C}_x)=-K_X\cdot {\mathcal K}-2=i_XH\cdot {\mathcal K}-2$ .

Given a Fano manifold X of Picard number $1$ , once the VMRT ${\mathcal C}_x\subset \mathbb {P}(\Omega _{X,x})$ of X can be explicitly determined and the VMRT is not dual defective, then Proposition 4.3 is quite useful to check whether the normalised tangent bundle of X is pseudoeffective or not. For Conjecture 1.6, we recall the following results for curves and surfaces.

Theorem 4.4 ([51, Theorem 2.1] [56, Propositions 3.1 and 3.2])

1. (1) Let $C\subset \mathbb {P}^N$ be a linearly nondegenerate smooth projective curve of degree d and codegree $d^*$ . Then the following statements hold.

   • (1.1) $d^*\geq 2d-2$ with equality if and only if C is a rational curve.

   • (1.2) $d^*\geq 2N-2$ with equality if and only if C is a normal rational curve.

2. (2) Let $S\subset \mathbb {P}^N$ be a linearly nondegenerate smooth projective surface of degree d and codegree $d^*$ . Then the following statements hold.

   • (2.1) $d^*\geq d-1$ with equality if and only if S is isomorphic to the Veronese surface $\nu _2(\mathbb {P}^2)\subset \mathbb {P}^5$ or its isomorphic projection in $\mathbb {P}^4$ , and $d^*=d$ if and only if S is a scroll over a curve and the cases $1\leq d^*-d\leq 2$ do not happen.

   • (2.2) $d^*\geq N-2$ with equality if and only if S is isomorphic to the Vernoese surface $\nu _2(\mathbb {P}^2)\subset \mathbb {P}^5$ , and $d^*=N-1$ if and only if S is either an isomorphic projection of $\nu _2(\mathbb {P}^2)$ to $\mathbb {P}^4$ or a rational normal scroll and the cases $0\leq d^*-N\leq 1$ do not happen.

4.B Projective threefolds with small codegree

This subsection is devoted to prove Proposition 1.8, which confirms Conjecture 1.6 for smooth threefolds. We start with a classification of projective threefolds, such that its general hyperplane section is a smooth surface with equal sectional genus and irregularity. Let us recall that for an n-dimensional polarised projective manifold $(X,L)$ , the sectional genus of X (with respect to L) is defined to be:

$$\begin{align*}g(X,L):=\frac{(K_X+(n-1)L)\cdot L^{n-1}}{2}+1. \end{align*}$$

Lemma 4.5. Let $Z\subsetneq \mathbb {P}^N$ be an irreducible, smooth and linearly nondegenerate projective threefold and denote by L the restriction ${\mathcal O}_{\mathbb {P}^N}(1)|_Z$ . Let S be a general smooth hyperplane section of Z. Assume that the sectional genus g of S is equal to the irregularity q of S. Then $(Z,L)$ is isomorphic to one of the following varieties:

1. (1) the three-dimensional quadric hypersurface $(\mathbb {Q}^3,{\mathcal O}_{\mathbb {Q}^3}(1))$ and $\operatorname *{\mathrm {codeg}}(Z)=2$ or

2. (2) a three-dimensional scroll, that is, a projective bundle $\mathbb {P}(E)\rightarrow B$ over a smooth curve B, such that all fibres are linearly embedded and L is the tautological line bundle ${\mathcal O}_{\mathbb {P}(E)}(1)$ . In particular, the dual defect of $Z=\mathbb {P}(E)$ is equal to $1$ and $\operatorname *{\mathrm {codeg}}(Z)=\deg (Z)=c_1(E)$ .

Proof. Denote by $\bar {L}$ the restriction $L|_S$ . As $g=q$ , by [53] (see also [49, Corollary 1.5.2]), we know that either S is a geometrically ruled surface with smooth $C\in |\bar {L}|$ as sections or the pair $(S,\bar {L})$ is isomorphic to one of the following:

$$ \begin{align*} (\mathbb{P}^2,{\mathcal O}_{\mathbb{P}^2}(1))\quad \text{or} \quad (\mathbb{P}^2,{\mathcal O}_{\mathbb{P}^2}(2)). \end{align*} $$

First, we note that the case $(S,\bar {L})=(\mathbb {P}^2,{\mathcal O}_{\mathbb {P}^2}(2))$ does not happen. This was already proved by Gaetano Scorza. Indeed, by Bott’s formula, we have $H^1(\mathbb {P}^2,T_{\mathbb {P}^2}(-2))=0$ . Then we can apply Zak’s inextendibility theorem (see [54]) to conclude that Z is a cone over S. In particular, Z is singular, which is a contradiction.

Next, we assume that the pair $(S,\bar {L})$ is isomorphic to $(\mathbb {P}^2,{\mathcal O}_{\mathbb {P}^2}(1))$ . Then, we have $L^3=\bar {L}^2=1$ . In particular, $(Z,L)$ itself is isomorphic to $(\mathbb {P}^3,{\mathcal O}_{\mathbb {P}^3}(1))$ , which contradicts our assumption.

Finally, we assume that S is a geometrically ruled surface over a smooth curve. According to [30, Theorem 1.3], the pair $(Z,L)$ is one of the following varieties:

1. (1) $(\mathbb {Q}^3,{\mathcal O}_{\mathbb {Q}^3}(1))$ ;

2. (2) $(\mathbb {P}^3,{\mathcal O}_{\mathbb {P}^3}(2))$ or

3. (3) there exists a vector bundle E of rank $3$ over B, such that $Z=\mathbb {P}(E)$ and S is an element in the linear system $|{\mathcal O}_{\mathbb {P}(E)}(1)|$ .

In Case (1), it is clear that $Z\subset \mathbb {P}^N$ is linearly normal, and, hence, it is a quadric hypersurface of $\mathbb {P}^4$ . In Case (2), one can easily obtain that $g(S)=1$ , while $q(S)=0$ , which does not satisfy our assumption. In Case (3), we note that $Z\subset \mathbb {P}^N$ is actually a three-dimensional scroll, such that all the fibres of $\mathbb {P}(E)\rightarrow B$ are linearly embedded. As B is a curve, it is well known that the dual defect of Z is equal to $1$ in this case (see, for instance, [50, Theorem 7.21]) and the fact $\operatorname *{\mathrm {codeg}}(Z)=\deg (Z)=c_1(E)$ follows from Lemma 4.6 below.

Lemma 4.6. Let $Z=\mathbb {P}(E)\subset \mathbb {P}^N$ be a three-dimensional scroll over a smooth projective curve B, such that ${\mathcal O}_{\mathbb {P}(E)}(1)\cong {\mathcal O}_{\mathbb {P}^N}(1)|_Z$ . Then we have:

$$\begin{align*}\operatorname*{\mathrm{codeg}}(Z)=\deg(Z)=c_1(E). \end{align*}$$

Proof. Let H be a hyperplane section of Z and denote by $\pi :\mathbb {P}(E)\rightarrow B$ the natural projection. By [1] (see also [50, Theorem 6.1]), we have:

$$\begin{align*}\operatorname*{\mathrm{codeg}}(Z)= c_2({\mathcal J}(H))\cdot H=c_1(\Omega_Z\otimes H)\cdot H^2 + c_2(\Omega_Z\otimes H)\cdot H, \end{align*}$$

where ${\mathcal J}(H)$ is the first jet bundle. By a straightforward computation, we get:

$$\begin{align*}c_1(\Omega_Z)=\pi^*c_1(E)+\pi^*K_C-3H, \end{align*}$$

and:

$$\begin{align*}c_2(\Omega_Z)=-3\pi^*K_C\cdot H-2\pi^*c_1(E)\cdot H + 3H^2. \end{align*}$$

As a consequence, we obtain $\operatorname *{\mathrm {codeg}}(Z)=c_1(E)\cdot H^2=H^3=\deg (Z)$ .

Remark 4.7. Zak informed us of a geometric proof of Lemma 4.6 which is valid for scrolls of any dimension. We keep the proof here to indicate how to use the formula given in [1] to compute the codegree of an arbitrary variety, and this method will also be used in Lemma A.2 to compute the codegree of the VMRT of $F_4/P_3$ .

Now we are in the position to prove Proposition 1.8.

Proof of Proposition 1.8

Denote by L the restriction of ${\mathcal O}_{\mathbb {P}^N}(1)|_Z$ , and let $S\subset Z$ be a general hyperplane section. According to Lemma 4.6, we shall assume that Z is not dual defective (cf. [50, Example 7.6]). By the codegree formula (cf. [27, Proposition 1.1]), we have:

(4.3) $$ \begin{align} d^*=(b_3(Z)-b_1(Z))+2(b_2(S)-b_2(Z))+2(g(S)-q(S)). \end{align} $$

Set $A=b_3(Z)-b_1(Z)$ , $B=b_2(S)-b_2(Z)$ and $C=2(g(S)-q(S))$ . Then both A and C are even nonnegative integers and B is a positive integer since Z is not dual defective by our assumption (see [27, Propositions 1.2 and 1.4]). If $C=0$ , then we can conclude by Lemma 4.5 that Z satisfies $d^*=d$ . Hence, we may assume also that $C>0$ in the sequel. On the other hand, if $p_g(S)\not =0$ , then it follows from [27, Proposition 2.5] that we have $g(S)-q(S)\geq N-1$ . In particular, we obtain:

$$\begin{align*}d^*\geq 2B+2(g(S)-q(S))\geq 2+2(N-1)=2N. \end{align*}$$

From now on, we shall assume that $B>0$ , $C>0$ and $p_g(S)=0$ . In particular, it follows [49, Theorem 1.5] that $K_S+\bar {L}$ is globally generated and [49, Proposition 2.1] implies that we have:

$$\begin{align*}d=\bar{L}^2\leq K_S^2+4g(S)-4, \end{align*}$$

where $\bar {L}$ is the restriction $L|_S$ and the equality holds if and only if $\Phi _{|K_S+\bar {L}|}$ is not generically finite, that is, $\dim (\Phi _{|K_S+\bar {L}|}(S))\leq 1$ . In particular, S is uniruled and so is Z. On the other hand, by Noether’s formula, we have:

$$\begin{align*}K_S^2=12\chi({\mathcal O}_S)-\chi_{\mathrm{top}}(S)=10-8q(S)-h^{1,1}(S). \end{align*}$$

This implies:

$$\begin{align*}d\leq 6+4g(S)-8q(S)-h^{1,1}(S). \end{align*}$$

Applying the codegree formula (4.3), we get:

$$ \begin{align*} d & \leq 6+2(d^*-2B-A)-4q(S)-h^{1,1}(S) \\ & \leq 2d^*+6-4(B+q(S))-2A-h^{1,1}(S). \end{align*} $$

Note that $q(S)$ and A are nonnegative integers. Thus, since B and $h^{1,1}(S)=b_2(S)$ are positive integers, it follows that we have $d\leq 2d^*$ unless the following condition happens:

$$\begin{align*}B=h^{1,1}(S)=b_2(S)=1\quad \mathrm{and}\quad A=q(S)=0. \end{align*}$$

This is impossible since we have $b_2(S)>b_2(Z)\geq 1$ by our assumption. Moreover, an easy similar argument shows that if the equality $d=2d^*$ holds, then we must have:

$$\begin{align*}B=1,\quad h^{1,1}(S)=b_2(S)=2\quad \mathrm{and}\quad A=q(S)=0. \end{align*}$$

This implies that $\rho (Z)=b_2(Z)=1$ . In particular, as Z is uniruled, it follows that Z is a Fano threefold of Picard number $1$ . Note that $(K_Z+2L)|_S=K_S+\bar {L}$ is globally generated but not big. This implies that $-K_Z=2L$ . In particular, the pair $(Z,L)$ is isomorphic to either $(\mathbb {P}^3,{\mathcal O}_{\mathbb {P}^3}(2))$ or a del Pezzo threefold. If Z is a del Pezzo threefold, then S is a del Pezzo surface with $b_2(S)=2$ and $-K_S=\bar {L}$ . However, according to the classification of del Pezzo threefolds of Picard number $1$ , we must have $d=\bar {L}^2=K_S^2\leq 5$ . This implies that $b_2(S)\geq 4$ , which is a contradiction. Hence, $2d^*=d$ if and only if $(Z,L)$ is isomorphic to $(\mathbb {P}^3,{\mathcal O}_{\mathbb {P}^3}(2))$ ; that is, the projective variety $Z\subset \mathbb {P}^N$ is projectively equivalent to either the second Veronese variety $\nu _2(\mathbb {P}^3)\subset \mathbb {P}^9$ or its isomorphic projection in $\mathbb {P}^8$ .

Finally, we assume that Z satisfies the equality (1.2). Then we have $5d^*=2(N+1)$ . In particular, by our results above, we must have:

$$\begin{align*}\frac{4(N+1)}{5}=2d^*\geq d\geq N-2. \end{align*}$$

This implies $N\leq 14$ and $d^*\leq 6$ . Then, by the classification of smooth projective threefolds of codegree at most $6$ given in [27], one can easily check that the only possibilities are the quadric threefold $\mathbb {Q}^3\subset \mathbb {P}^4$ (with $d^*=2$ ) and the Veronese variety $\nu _2(\mathbb {P}^3)\subset \mathbb {P}^9$ (with $d^*=4$ ).

4.C Proof of Theorem 1.9

We start with the following classification of del Pezzo surfaces with pseudoeffective normalised tangent bundle, which is easily deduced from [38, IV, Theorem 4.8].

Theorem 4.8. Let S be a smooth del Pezzo surface, that is, $-K_S$ is ample. Then the normalised tangent bundle of S is pseudoeffective if and only if S is isomorphic to the quadric surface $\mathbb {P}^1\times \mathbb {P}^1$ .

Proof. Note that $T_S$ is always semistable with respect to $-K_S$ by [9], and its normalisation is not nef by Theorem 1.1. On the other hand, since S is simply connected, there does not exist nontrivial unramified coverings of S. In particular, applying [38, IV, Theorem 4.8] to S and $T_S$ , we see that only Case (A) and Case (C) of [38, IV, Theorem 4.8] may happen in our situation. In other words, either $T_S$ splits as a direct sum $L_1\oplus L_2$ as in Case (A) or $-K_S\equiv 2L$ for some line bundle L on S as in Case (C). In the latter case, it is easy to see that S is isomorphic to the quadric surface from the classification of del Pezzo surfaces. In the former case, the surface S is isomorphic to a product of curves (see, for instance, [13, Theorem 1.4]). This implies immediately that S is isomorphic to the product $\mathbb {P}^1\times \mathbb {P}^1$ as S is rationally connected.

From now on, we will assume that $n \geq 3$ . To prove Theorem 1.9, we start with the following:

Theorem 4.9. Let X be an n-dimensional Fano manifold of Picard number $1$ equipped with a dominating family ${\mathcal K}$ of minimal rational curves. Assume that the VMRT ${\mathcal C}_x\subset \mathbb {P}(\Omega _{X,x})$ at a general point $x\in X$ is not dual defective. If $\dim ({\mathcal C}_x)\geq 1$ and $n\geq 3$ , then $\operatorname *{\mathrm {codeg}}({\mathcal C}_x)\geq 2$ and the following statements hold.

1. (1) If $\operatorname *{\mathrm {codeg}}({\mathcal C}_x)=2$ , then X is a smooth quadric hypersurface in $\mathbb {P}^{n+1}$ .

2. (2) If the normalised tangent bundle of X is pseudoeffective and the VMRT ${\mathcal C}_x$ is smooth with $\operatorname *{\mathrm {codeg}}({\mathcal C}_x)=3$ , then X is one of the following varieties: the Lagrangian Grassmann variety $\mathrm LG(3,6)$ , the Grassmann variety $\mathrm {Gr}(3,6)$ , the $15$ -dimensional spinor variety $\mathbb {S}_6$ or the $27$ -dimensional $E_7$ -variety $E_7/P_7$ .

Proof. By the biduality theorem, the dual variety $\check {{\mathcal C}}_x$ does not contain hyperplanes as irreducible components since ${\mathcal C}_x$ is purely dimensional, and, hence, $\operatorname *{\mathrm {codeg}}({\mathcal C}_x)\geq 2$ . Let us denote by $\mathbb {P}^m=\mathbb {P}(W)\subset \mathbb {P}(\Omega _{X,x})$ the linear span of ${\mathcal C}_x$ .

First, we assume that $\operatorname *{\mathrm {codeg}}({\mathcal C}_x)=2$ , that is, the dual $\check {{\mathcal C}}_x\subset \mathbb {P}(T_{X,x})$ is an irreducible quadric hypersurface of $\mathbb {P}(T_{X,x})$ . Then the VMRT ${\mathcal C}_x$ itself is irreducible. On the other hand, if $\check {{\mathcal C}}_x$ is not smooth, then it is an irreducible quadric cone. According to the biduality theorem, since ${\mathcal C}_x$ is not dual defective, the VMRT ${\mathcal C}_x$ is a smooth quadric hypersurface in $\mathbb {P}^m\subset \mathbb {P}(\Omega _{X,x})$ . Then it follows from [18, Propositions 2.4 and 2.6] that we must have $\mathbb {P}^m=\mathbb {P}(\Omega _{X,x})$ . Therefore, by Theorem 1.5, the variety X is isomorphic to a quadric hypersurface.

Next, we assume that ${\mathcal C}_x$ is smooth with $\operatorname *{\mathrm {codeg}}({\mathcal C}_x)=3$ and the normalised tangent bundle of X is pseudoeffective. Then, $\check {{\mathcal C}}_x$ is an irreducible hypersurface of degree $3$ , and, hence, ${\mathcal C}_x$ is irreducible and smooth. By Zak’s classification of linearly nondegenerate smooth varieties with codegree $3$ [55, Theorem 5.2], we obtain that $\dim ({\mathcal C}_x)\geq 2$ and:

$$\begin{align*}\dim({\mathcal C}_x)>\frac{m-1}{2}, \end{align*}$$

unless ${\mathcal C}_x\subset \mathbb {P}^m$ is $\nu _2(\mathbb {P}^2)\subset \mathbb {P}^5$ . On the other hand, it can be directly checked that the tangential variety of $\nu _2(\mathbb {P}^2)\subset \mathbb {P}^5$ is linearly nondegenerate. Therefore, it follows from [18, Proposition 2.6] that the tangential variety of ${\mathcal C}_x$ is linearly nondegenerate. Then we can apply [18, Proposition 2.4] to obtain that $\mathbb {P}^m=\mathbb {P}(\Omega _{X,x})$ . In particular, as ${\mathcal C}_x$ is assumed to be not dual defective, it follows from Proposition 4.3 that ${\mathcal C}_{x}\subset \mathbb {P}(\Omega _{X,x})$ is projectively equivalent to one of the four Severi varieties. Then one can apply Theorem 1.5 to conclude that X is isomorphic to one of the four varieties in the theorem.

Compared with Proposition 4.3, we do not require that the VMRT of X at a general point is irreducible or linearly nondegenerate in Theorem 4.9 above.

Proof of Theorem 1.9

For statement (1), we assume that the VMRT ${\mathcal C}_x\subset \mathbb {P}(\Omega _{X,x})$ is irreducible, linearly nondegenerate and not dual defective. Let $\check {{\mathcal C}}\subset \mathbb {P}(T_X)$ be the total dual VMRT. Write $[\check {{\mathcal C}}]\equiv a\Lambda - b\pi ^*H$ , where $\Lambda $ is the tautological divisor of the projectivised tangent bundle $\pi :\mathbb {P}(T_X)\rightarrow X$ and H is the ample generator of $\operatorname *{\mathrm {Pic}}(X)$ . Let $i_X$ be the index of X. Without loss of generality, we may assume that $\alpha (X,-K_X)>0$ , or equivalently, $T_X$ is big. In particular, by Theorem 3.4, we have $b>0$ and:

$$\begin{align*}\alpha(X,-K_X) = \frac{b}{a i_X} =\frac{b}{i_X \operatorname*{\mathrm{codeg}}({\mathcal C}_x)}\leq \frac{b}{i_X}\cdot \frac{\dim({\mathcal C}_x)+2}{2\dim(X)}. \end{align*}$$

The last inequality follows from the Segre inequality (1.1). In particular, note that we have $\dim ({\mathcal C}_x)+2=-K_X\cdot {\mathcal K} = i_X H \cdot {\mathcal K}$ and $bH\cdot {\mathcal K}\leq 2$ , thus, we get:

$$\begin{align*}\alpha(X,-K_X)\leq \frac{1}{\dim(X)} \end{align*}$$

with equality only if the VMRT ${\mathcal C}_x\subset \mathbb {P}(\Omega _{X,x})$ satisfies the equality (1.2). Hence, if the normalised tangent bundle of X is pseudoeffective and Conjecture 1.6 holds, then the VMRT ${\mathcal C}_x\subset \mathbb {P}(\Omega _{X,x})$ is projectively equivalent to one of the varieties listed in Conjecture 1.6 and we then conclude by Theorem 1.5 and Table 1.

For statement (2), assume that the VMRT ${\mathcal C}_x\subset \mathbb {P}(\Omega _{X,x})$ is not dual defective and the normalised tangent bundle of X is pseudoeffective. By Proposition 4.3, if the condition (2.1) (respectively, condition (2.2)) holds, then we get $\operatorname *{\mathrm {codeg}}({\mathcal C}_x)<3$ (respectively, $\operatorname *{\mathrm {codeg}}({\mathcal C}_x)<4$ ) and the results follow from Theorem 4.9 above. If the condition (2.3) holds, then it is clear that $\dim ({\mathcal C}_x)\geq 1$ as the VMRT can not be a single point. Then the result follows from statement (1.2), Proposition 1.8 and Theorem 4.4.

Proof of Corollary 1.10

By assumption, the VMRT ${\mathcal C}_x\subset \mathbb {P}(\Omega _{X,x})$ is either a nonlinear smooth curve, a nonlinear smooth surface or a nonlinear smooth hypersurface $(n=5)$ . In particular, the VMRT ${\mathcal C}_x$ is not dual defective by [50, Examples 1.19 and 7.5 and Theorem 4.25]. Then the result follows directly from Theorem 1.9 (2.2).

Proof of Corollary 1.12

The result follows from Theorem 1.9 (2.2) and (2.3).

5 Rational homogeneous spaces

Throughout this section, for a vector bundle E over a variety X, we denote by $\mathbf {P}(E)$ the projective bundle over X, whose fibre over $x \in X$ is the set of lines in $E_x$ . It is isomorphic to $\mathbb {P}(E^*)$ in our previous notation. Moreover, all the varieties in this section are assumed to have dimension at least $2$ . The main aim of this section is to calculate the cones of divisor of $\mathbf {P}(T^*_{G/P}) = \mathbb {P} (T_{G/P})$ for a rational homogeneous space $G/P$ with Picard number $1$ .

5.A Springer maps

Let G be a complex simple Lie algebra, and let $\mathfrak {g}$ be its Lie algebra. Then G has the adjoint action on $\mathfrak {g}$ . The orbit ${\mathcal O}_x$ of a nilpotent element $x\in \mathfrak {g}$ is called a nilpotent orbit, which is invariant under the dilation action of $\mathbb {C}^*$ on $\mathfrak {g}$ . For any parabolic subgroup P of G, the group G has a Hamiltonian action on the cotangent bundle $T^*_{G/P}$ and the image of the moment map $ T^*_{G/P}\longrightarrow \mathfrak {g} \simeq \mathfrak {g}^*$ is a nilpotent orbit closure $\overline {{\mathcal O}}$ , which will be called the Richardson orbit associated to P. The induced morphism:

$$ \begin{align*} \widehat{s}: T^*_{G/P}\rightarrow \overline{{\mathcal O}} \end{align*} $$

will be called the Springer map associated to P, which is a generically finite $G \times \mathbb {C}^*$ -equivariant projective morphism. We denote by:

$$\begin{align*}T^*_{G/P} \xrightarrow{\widehat{\varepsilon}} \widetilde{{\mathcal O}} \xrightarrow{\widehat{\tau}} \overline{{\mathcal O}} \end{align*}$$

the Stein factorisation of $\widehat {s}$ . It follows that $\widehat {\varepsilon }$ is birational and $\widehat {\tau }$ is a finite morphism. Note that $\widehat {s}^{-1}(0) = G/P$ is irreducible, the pre-image $\widehat {\tau }^{-1}(0)$ is a single point in $\widetilde {{\mathcal O}}$ . This implies that the projectivised Springer map:

$$ \begin{align*} s: \mathbf{P} (T^*_{G/P})\rightarrow \mathbf{P}(\overline{{\mathcal O}}) \end{align*} $$

has the Stein factorisation given by:

$$\begin{align*}\mathbf{P} (T^*_{G/P}) \xrightarrow{\varepsilon} \mathbf{P}(\widetilde{{\mathcal O}}) \xrightarrow{\tau} \mathbf{P}(\overline{{\mathcal O}}). \end{align*}$$

From now on, we shall assume that $G/P$ is a rational homogeneous space with Picard number $1$ ; that is, P corresponds to a single-marked Dynkin diagram.

Example 5.1. Given an $(n+1)$ -dimensional complex vector space V, the rational homogeneous spaces for the group $SL_{n+1}=SL_{n+1}(V)$ , are determined by the different markings of the Dynkin diagram $A_n$ . For instance, the Grassmann variety $\mathrm {Gr}(k,n+1)$ corresponds to the marking of the k-th node:

Proposition 5.2 39, Proposition 5.1

Assume $G/P$ is of Picard number $1$ . Then the projectivised Springer map $s: \mathbf {P} (T^*_{G/P})\rightarrow \mathbf {P}(\overline {{\mathcal O}})$ is birational and small if and only if $G/P$ is one of the following:

Furthermore, the pair $(P, Q)$ in each group has the same Richardson orbit and the corresponding Springer maps give a birational map

, which is called the stratified Mukai flop of type $A_{n,k}$ (respectively, $D_n, E_{6, I}, E_{6, II}$ ) according to the types of corresponding marked Dynkin diagrams. In this case, there exists a (noncanonical) isomorphism $G/P \simeq G/Q$ .

Proposition 5.3 (40, Proposition 3.1)

Assume $G/P$ is of Picard number $1$ . Then the birational contraction $\varepsilon : \mathbf {P} (T^*_{G/P}) \to \mathbf {P}(\widetilde {{\mathcal O}}) $ is small if and only if either $G/P$ is as in Proposition 5.2 or $\widehat {s}$ has degree 2 and $G/P$ is one of the following:

In the latter case, by interchanging the two points in general fibres of $\widehat {s}$ , this gives a stratified Mukai flop of type $B_{n,k}$ (respectively, $C_{n,k}, D_{n,k}$ )

according to the types of corresponding marked Dynkin diagrams.

We will describe these flops in detail in Section 5.D.

Proposition 5.4. The Springer map $\widehat {s}: T^*_{G/P} \to \overline {\mathcal {O}}$ is not birational if and only if $G/P$ is as in Proposition 5.3 or $G/P$ is $G_2/P_1$ or $F_4/P_3$ with $\mathrm {deg}(\widehat {s})$ being $2$ and $4$ , respectively.

Proof. For classical cases, this follows from the proof of [40, Proposition 3.1]. For exceptional cases, assume G is of exceptional type. In most cases, $\mathcal {O}$ is an even orbit or an orbit with trivial fundamental group, which implies that $\widehat {s}$ is birational. For the remaining cases, the degree is computed in [10, Appendix].

5.B Cones of divisors

We start with the following result, which describes the cones of divisors on $\mathbf {P} (T^*_{G/P}) = \mathbb {P} (T_{G/P})$ .

Theorem 5.5. Let $G/P$ be a rational homogeneous space of Picard number $1$ but not a projective space. Denote by H the ample generator of $\operatorname *{\mathrm {Pic}}(G/P)$ . Let $\Gamma $ be the exceptional locus of $\varepsilon : \mathbf {P} (T^*_{G/P}) \to \mathbf {P}(\widetilde {{\mathcal O}}) $ . Then the following statements hold.

1. (1) If $\Gamma $ has codimension at least $2$ , that is, $\varepsilon $ is small, then there exists a commutative diagram:

   

   where $\mu : \mathbf {P} (T^*_{G/P}) \dashrightarrow \mathbf {P} (T^*_{G/Q})$ is a nonisomorphic flop with $G/P \simeq G/Q$ . In particular, we have:

   $$\begin{align*}\mathrm{Eff}(\mathbf{P} (T^*_{G/P}))&=\overline{\mathrm{Eff}}(\mathbf{P} (T^*_{G/P}))=\mathrm{Mov}(\mathbf{P} (T^*_{G/P}))=\overline{\mathrm{Mov}}(\mathbf{P} (T^*_{G/P}))\\&=\left\langle [\mu^*\pi_2^*H],[\pi_1^*H]\right\rangle. \end{align*}$$

2. (2) If $\Gamma $ has codimension $1$ , that is, $\varepsilon $ is divisorial, then $\Gamma $ is a prime divisor, such that:

   $$\begin{align*}\mathrm{Mov}(\mathbf{P} (T^*_{G/P}))=\overline{\mathrm{Mov}}(\mathbf{P} (T^*_{G/P}))=\left\langle [\Lambda], [\pi^*H] \right\rangle \end{align*}$$
   and:
   $$\begin{align*}\mathrm{Eff}(\mathbf{P} (T^*_{G/P}))=\overline{\mathrm{Eff}}(\mathbf{P} (T^*_{G/P}))=\left\langle [\Gamma],[\pi^*H] \right\rangle. \end{align*}$$

Proof. Since $G/P$ is not isomorphic to projective spaces, the birational contraction $\varepsilon : \mathbf {P} (T^*_{G/P}) \to \mathbf {P}(\widetilde {{\mathcal O}}) $ is not an isomorphism and $\mathrm {Nef}(\mathbf {P} (T^*_{G/P}) )=\langle [\Lambda ],[\pi ^*H]\rangle $ . Let $\alpha (G/P, H)$ be the pseudoeffective threshold of $G/P$ with respect to H, then $[\Lambda -\alpha (G/P, H)\pi ^*H]$ generates an extremal ray of $\overline {\mathrm {Eff}}(\mathbf {P} (T^*_{G/P}) )$ . Statement (2) follows directly from Proposition 3.13. Thus, it remains to prove statement (1).

By our assumption, the birational contraction $\varepsilon $ is small. By Propositions 5.2 and 5.3, there exists a flop $\mu : \mathbf {P} (T^*_{G/P}) \dashrightarrow \mathbf {P} (T^*_{G/Q})$ , with $G/P \simeq G/Q$ as projective varieties. It follows that the pull-back $\mu ^*\mathrm {Nef}( \mathbf {P} (T^*_{G/Q}))$ is contained in $\overline {\mathrm {Mov}}( \mathbf {P} (T^*_{G/P}))$ (cf. Lemma 3.7). Moreover, it is clear that we have $\mu ^*\Lambda =\Lambda $ since $-K_{\mathbf {P} (T^*_{G/P})}=n\Lambda $ and $\mu $ is a SQM. This implies that the pull-back $\mu ^*\mathrm {Nef}(\mathbf {P} (T^*_{G/P}))$ is contained in the cone $\langle [\Lambda -\alpha (G/P, H)\pi _1^*H], [\Lambda ]\rangle $ . Nevertheless, as $\pi _2^*H$ is not big, it follows that $[\mu ^*\pi _2^*H]$ is not contained in the interior of $\overline {\mathrm {Eff}}(\mathbf {P} (T^*_{G/P}))$ . So we get:

$$\begin{align*}\overline{\mathrm{Eff}}(\mathbf{P} (T^*_{G/P}))=\overline{\mathrm{Mov}}(\mathbf{P} (T^*_{G/P}))=\langle [\mu^*\pi_2^*H], [\pi_1^*H]\rangle. \end{align*}$$

On the other hand, as $\pi _2^*H$ is globally generated and $\mu $ is a SQM, the stable base locus ${\mathbb B}(\mu ^*\pi _2 H)$ has codimension at least $2$ . Hence, we obtain:

$$\begin{align*}\overline{\mathrm{Eff}}(\mathbf{P} (T^*_{G/P}))=\mathrm{Eff}(\mathbf{P} (T^*_{G/P}))=\overline{\mathrm{Mov}}(\mathbf{P} (T^*_{G/P}))=\mathrm{ Mov}(\mathbf{P} (T^*_{G/P})). \end{align*}$$

This finishes the proof.

While Theorem 5.5 already gives a very nice geometric description of the cones of divisors of $\mathbf {P} (T^*_{G/P})$ , it is not very easy to apply it to compute explicitly the cones in terms of $\Lambda $ and $\pi ^*H$ . We introduce the following notion to divide $G/P$ into several types in order to carry out this computation.

Definition 5.6. Let $G/P$ be a rational homogeneous space of Picard number $1$ corresponding to a single marked Dynkin diagram.

1. (1) $G/P$ is said of the first type (I) if s is a birational small morphism (cf. Proposition 5.2).

2. (2) $G/P$ is said of type (II-s) if s is not birational and $\varepsilon $ is small (cf. Proposition 5.3).

3. (3) $G/P$ is said of type (II-d-d) if $\varepsilon $ is divisorial and the VMRT of $G/P$ is dual defective.

4. (4) $G/P$ is said of type (II-d-A1) (respectively, (II-d-A2)) if $\varepsilon $ is divisorial but the VMRT of $G/P$ is not dual defective and $\mathbf {P}(\widetilde {\mathcal {O}})$ is of type $A_1$ (respectively, $A_2$ ) (cf. Definition 3.11).

Remark 5.7. Recall there are following isomorphisms between different rational homogeneous spaces: $C_n/P_1 \simeq A_{2n}/P_1, B_n/P_n \simeq D_{n+1}/P_n$ and $G_2/P_1 \simeq B_3/P_1$ . Their types are the same except the following cases: $C_n/P_1$ is of type (II-s), while $A_{2n}/P_1$ is of type (I); and for n even, $B_n/P_n$ is of type (II-s), while $D_{n+1}/P_n$ is of type (I). In fact, note that $C_n/P_1 \simeq \mathbb {P}^{2n-1}$ . Let $\mathcal {O}_{min} \subset \mathfrak {sl}_{2n}$ be the minimal nilpotent orbit (corresponding to the partition $[2, 1^{2n-2}]$ ), then there exists a generically 2-to-1 morphism $\overline {\mathcal {O}}_{min} \to \mathcal {O}_{\mathbf {d}}$ . The flop $C_{n,1}$ is nothing else but the Mukai flop $A_{2n,1}$ . Moreover, by [40, Example 3.3], $B_{n, n}$ -flop is the same as $D_{n+1}$ -flop for n even.

Proposition 5.8. Under the notation and assumption as in Theorem 5.5. Assume that $\varepsilon $ is small. Let $\ell _i$ be a general line in a general fibre of $\pi _i$ . If $a(H)$ and $b(H)$ are the unique positive integers, such that:

$$\begin{align*}[\mu^*\pi_2^*H] \equiv a(H)[\Lambda] - b(H)[\pi_1^*H], \end{align*}$$

then we have:

$$\begin{align*}a(H)=\pi_2^*H\cdot \mu_*(\ell_1)\quad \mathrm{and}\quad a(H)-b(H)\pi_1^*H\cdot \mu^{-1}_*(\ell_2)=0. \end{align*}$$

Moreover, the morphism $\mu (\ell _1)\rightarrow \pi _2(\mu (\ell _1))$ is birational. In particular, we have:

$$\begin{align*}a(H)=H\cdot \pi_{2*}\mu_*(\ell_1). \end{align*}$$

Proof. Since $\mu $ is a SQM and $\ell _i$ ’s are general, we may assume that both $\mu $ and $\mu ^{-1}$ are isomorphisms in a neighborhood of $\ell _i$ . In particular, we have:

$$\begin{align*}a(H) = (a(H)\Lambda - b(H) \pi^*_1 H)\cdot \ell_1 = \mu^*\pi_2^*H\cdot \ell_1 = \pi_2^*H\cdot \mu_*(\ell_1) \end{align*}$$

and:

$$\begin{align*}0=\pi_2^*H\cdot \ell_2 = \mu^*\pi_2^*H \cdot \mu^{-1}_*(\ell_2) = a(H) - b(H)\pi_1^*H\cdot \mu^{-1}_*(\ell_2). \end{align*}$$

Here, we note that $\mu ^*\Lambda =\Lambda $ and $\Lambda \cdot \ell _i=1$ . Now it remains to show that the morphism $\mu (\ell _1)\rightarrow C:=\pi _2(\mu (\ell _1))$ is birational. Let $f:\mathbb {P}^1\rightarrow C$ be the normalisation. As $T_{G/Q}$ is nef, there exist integers $a_1\geq \dots \geq a_k>a_{k+1}=\dots =a_n=0$ (with $k\leq n$ ), such that:

$$\begin{align*}f^*T_{G/Q}\cong \bigoplus_{i=1}^k{\mathcal O}_{\mathbb{P}^1}(a_i)\oplus {\mathcal O}_{\mathbb{P}^1}^{\oplus (n-k)}. \end{align*}$$

Denote by d the degree of $\mu (\ell _1)\rightarrow C$ . Then we have:

$$\begin{align*}\pi_2^*T_{G/Q}|_{\mu(\ell_1)} \cong \bigoplus_{i=1}^k{\mathcal O}_{\mathbb{P}^1}(d a_i) \oplus {\mathcal O}_{\mathbb{P}^1}^{\oplus (n-k)}. \end{align*}$$

As $\Lambda \cdot \mu (\ell _1)=1$ , if $d\geq 2$ , then $\mu (\ell _1)$ is contained in:

$$\begin{align*}\mathbb{P}({\mathcal O}_{\mathbb{P}^1}^{\oplus (n-k)}) \subset \mathbb{P}(f^*T_{G/P}). \end{align*}$$

On the other hand, as $\mathbb {P}({\mathcal O}_{\mathbb {P}^1}^{\oplus (n-k)})$ is dominated by curves with $\Lambda $ -degree $0$ , thus, $\mathbb {P}({\mathcal O}_{\mathbb {P}^1}^{\oplus (n-k)})$ is contained in the exceptional locus of $\varepsilon $ and so is $\mu (\ell _1)$ , which is absurd.

Proposition 5.9. Under the notation and assumption as in Theorem 5.5. Assume that $\varepsilon : \mathbf {P} (T^*_{G/P}) \to \mathbf {P}(\widetilde {{\mathcal O}})$ is divisorial. Let $a(\Gamma )$ and $b(\Gamma )$ be the unique positive integers, such that:

$$\begin{align*}[\Gamma]\equiv a(\Gamma)[\Lambda] - b(\Gamma)\pi^*H. \end{align*}$$

Then the following statements hold.

1. (1) The projective variety $\mathbf {P}(\widetilde {\mathcal {O}})$ is a $\mathbb {Q}$ -factorial variety of Picard number $1$ . Moreover, let $\Lambda '$ and $H'$ be the push forward of $\Lambda $ and $\pi ^*H$ by $\varepsilon $ . Then we have:

   $$\begin{align*}\frac{b(\Gamma)}{a(\Gamma)}=\frac{\Lambda^{2n-1}}{\Lambda^{2n-2}\cdot \pi^*H}\quad \mathrm{and}\quad H'\equiv \frac{a(\Gamma)}{b(\Gamma)}\Lambda'. \end{align*}$$

2. (2) If $G/P$ is of type (II-d-A1) or (II-d-A2), then $a(\Gamma )=\operatorname *{\mathrm {codeg}}({\mathcal C}_o)$ , where ${\mathcal C}_o$ is the VMRT of $G/P$ at a referenced point $o\in G/P$ .

3. (3) $b(\Gamma )\leq 2$ with equality if and only if $G/P$ is of type (II-d-A1).

4. (4) $G/P$ is of type (II-d-A2) if and only if $\mathbf {P}(\widetilde {\mathcal {O}})$ has $cA_2$ -singularities in codimension $2$ .

Proof. First, note that the morphism $\varepsilon $ is a Mori extremal contraction with respect to a klt pair $(\mathbf {P}(T^*_{G/P}),\Delta )$ (see [37, Proposition 5.5]). Thus, as $\rho (\mathbf {P}(T^*_{G/P}))=2$ , $\varepsilon $ is divisorial and $\mathbf {P}(T^*_{G/P})$ is rationally connected, it follows that $\mathbf {P}(\widetilde {\mathcal {O}})$ is a $\mathbb {Q}$ -factorial Fano variety of Picard number $1$ . Moreover, note that we have $\Gamma \cdot \Lambda ^{2n-2}=0$ . This implies immediately:

$$\begin{align*}\frac{b(\Gamma)}{a(\Gamma)}=\frac{\Lambda^{2n-1}}{\Lambda^{2n-2}\cdot \pi^*H}. \end{align*}$$

Let $\widetilde {H}$ be a general member in $|\pi ^*H|$ , and set $H'=\varepsilon _*\widetilde {H}$ . As $\mathbf {P}(\widetilde {\mathcal {O}})$ is $\mathbb {Q}$ -factorial, there exists a rational number r, such that $H'\equiv r \Lambda '$ . Moreover, by the negativity lemma, there exists a nonnegative rational number $\alpha $ , such that:

$$\begin{align*}\varepsilon^*H' \equiv_{\mathbb{Q}} \widetilde{H} + \alpha \Gamma. \end{align*}$$

As $\varepsilon ^*\Lambda '=\Lambda $ , we obtain:

$$\begin{align*}r\Lambda \equiv \varepsilon^*H' \equiv \pi^*H + \alpha(a(\Gamma)\Lambda-b(\Gamma)\pi^*H). \end{align*}$$

Since $\Lambda $ and $\pi ^*H$ are linearly independent, comparing the coefficients shows that we have:

$$\begin{align*}\alpha b(\Gamma)=1 \quad \mathrm{and}\quad \alpha a(\Gamma)=r. \end{align*}$$

This implies $r=a(\Gamma )/b(\Gamma )$ , and statement (1) is proved.

If $G/P$ is of types (II-d-A1) or (II-d-A2), the total dual VMRT is a divisor. It follows from Corollary 2.5, Theorem 3.4 and Proposition 3.13 that we have $\check {{\mathcal C}}=\Gamma $ , and, hence, $a(\Gamma )=\operatorname *{\mathrm {codeg}}({\mathcal C}_o)$ .

For statement (3), by Proposition 3.13, we have $b(\Gamma )\leq 2$ with equality if and only if $\mathbf {P}(\widetilde {\mathcal {O}})$ is of type $A_1$ and there exists a dominating family ${\mathcal K}$ of minimal rational curves on $G/P$ , such that $\check {{\mathcal C}}=\Gamma $ and $H\cdot {\mathcal K}=1$ . Note that in our situation, there exists only one dominating family ${\mathcal K}$ of minimal rational curves on $G/P$ and $H\cdot {\mathcal K}=1$ . Thus, $b(\Gamma )=2$ if and only if $\check {{\mathcal C}}=\Gamma $ and $\mathbf {P}(\widetilde {\mathcal {O}})$ is of type $A_1$ . The latter conditions are equivalent to say that $G/P$ is of type (II-d-A1) by definition.

For statement (4), if $G/P$ is of type (II-d-A2), it follows from definition that $\mathbf {P}(\widetilde {\mathcal {O}})$ has $cA_2$ singularities in codimension $2$ . Conversely, from the proof of Proposition 3.13, it is known that $b(\Gamma )\pi ^*H\cdot F\leq 2$ with equality if and only if $\Gamma $ is smooth along F, where F is an irreducible component of a general fibre of $\Gamma \rightarrow \varepsilon (\Gamma )$ . In particular, if $\mathbf {P}(\widetilde {\mathcal {O}})$ has $cA_2$ -singularities in codimension $2$ , then we must have $b(\Gamma )=\pi ^*H\cdot F=1$ . Then Claim 2 in the proof of Proposition 3.13 implies that $\check {{\mathcal C}}=\Gamma $ and consequently $G/P$ is of type (II-d-A2).

As an immediate application of Proposition 5.9, one can easily derive the following result.

Corollary 5.10. Under the notation and assumption as in Theorem 5.5. Assume that $\varepsilon $ is divisorial. Then the following statements hold.

1. (1) $G/P$ is of type (II-d-d) if and only if $\check {{\mathcal C}}\not =\Gamma $ and if and only if $b(\Gamma )=1$ and $\mathbf {P}(\widetilde {\mathcal {O}})$ has only $cA_1$ singularities in codimension $2$ .

2. (2) $G/P$ is of type (II-d-A1) if and only if $b(\Gamma )=2$ and $\check {{\mathcal C}}=\Gamma $ and if and only if $\mathbf {P}(\widetilde {\mathcal {O}})$ has $cA_1$ -singularities in codimension $2$ and $\check {{\mathcal C}}=\Gamma $ .

3. (3) $G/P$ is of type (II-d-A2) if and only if $b(\Gamma )=1$ and $\check {{\mathcal C}}=\Gamma $ and if and only if $\mathbf {P}(\widetilde {\mathcal {O}})$ has $cA_2$ -singularities in codimension $2$ .

5.C Types of rational homogeneous spaces

By Propositions 5.8 and 5.9 in the previous subsection, to compute $a(E)$ , $b(E)$ , $a(H)$ and $b(H)$ , we need to determine the types of $G/P$ . Propositions 5.2 and 5.3 give, respectively, the classification of $G/P$ of type (I) and type (II-s). In this subsection, we will determine the types of all other $G/P_k$ , where $P_k$ is the maximal parabolic subgroup associated to the k-th simple root of G.

The VMRT $\mathcal {C}_o$ of $G/P_k$ is determined in [26, Theorem 4.8], which is again a rational homogeneous space if $P_k$ corresponds to a long root. When $P_k$ corresponds to a short root, $\mathcal {C}_o$ is a two-orbit variety. The embedding $\mathcal {C}_o \subset \mathbf {P}(T_{G/P,o})$ is in general degenerated, and the dual defect of $\mathcal {C}_o$ can be computed from the following when it is homogeneous (cf. [48], [50, Theorems 7.54 and 7.56]).

Proposition 5.11. Let $G/P \subset \mathbb {P}^N$ be the minimal G-equivariant embedding. Then it is dual defective if and only if $G/P$ is one of the following:

1. (a) $ \mathbb {P}^n$ with $\mathrm {def} = n$ ;

2. (b) $\mathrm {Gr}(2, 2m+1) $ with $\mathrm {def} = 2$ ;

3. (c) the ten-dimensional spinor variety $\mathbb {S}_5$ with $\mathrm {def} = 4$ ;

4. (d) a product $G_1/P_1 \times G_2/P_2$ with $G_1/P_1$ as above, such that $\mathrm {def}(G_1/P_1)> \dim G_2/P_2$ . In this case, the dual defect is $\mathrm {def} = \mathrm {def}(G_1/P_1) - \dim G_2/P_2 $ .

Proposition 5.12. Let $X=G/P_k$ be a rational homogeneous space, such that $P_k$ corresponds to a short root. Then the VMRT ${\mathcal C}_o$ of X is dual defective if and only if X is one of the following:

$$\begin{align*}B_n/P_n\ (n\geq 3\ \mathrm{odd}),\quad C_n/P_k\ (2n\geq 3k)\quad \text{or}\quad F_4/P_4. \end{align*}$$

Proof. If $X=G/P_k$ is one of the following: $B_n/P_n$ , $C_n/P_1$ and $G_2/P_1$ , then it is isomorphic, respectively, to $D_{n+1}/P_{n+1}$ , $A_{2n-1}/P_1$ and $B_3/P_1$ . In particular, the VMRT of X is still a rational homogeneous space in these cases, and we can apply Proposition 5.11. If $X=G/P_k$ is the rational homogeneous space of type $C_n/P_k$ with $k\geq 2$ , it is shown in Lemma A.1 that the VMRT ${\mathcal C}_o\subset \mathbb {P}(\Omega _{X,o})$ is dual defective if and only if $2n\geq 3k$ . If $X=G/P_k$ is the variety $F_4/P_3$ , then it is shown in Lemma A.2 that the VMRT ${\mathcal C}_o\subset \mathbb {P}(\Omega _{X,o})$ is not dual defective with codegree $8$ . If $X=G/P_k$ is the variety $F_4/P_4$ , then the VMRT ${\mathcal C}_o\subset \mathbb {P}(\Omega _{X,o})$ is a hyperplane section of $\mathbb {S}_5\subset \mathbb {P}^{15}$ . Recall that the dual defect of $\mathbb {S}_5\subset \mathbb {P}^{15}$ is equal to $4$ , thus, the dual defect of the VMRT ${\mathcal C}_o\subset \mathbb {P}(\Omega _{X,o})$ is $3$ by [50, Theorem 5.3].

Now we determine the singularity type of $\mathbf {P}(\widetilde {\mathcal {O}})$ .

Proposition 5.13. Assume that $\varepsilon : \mathbf {P}(T^*_{G/P}) \to \mathbf {P}(\widetilde {\mathcal {O}})$ is divisorial and the VMRT of $G/P$ is not dual defective. Then $\mathbf {P}(\widetilde {\mathcal {O}})$ is of type $A_1$ except for $G/P = E_7/P_4$ , which is of type $A_2$ .

Proof. Consider first the case where $\widehat {s}$ is birational, then $\mathbf {P}(\widetilde {\mathcal {O}})$ is just the normalisation of $\mathbf {P}(\overline {\mathcal {O}})$ , whose generic singularity type is determined in [11]. It turns out only for $E_7/P_4$ , the generic singularity is of type $A_2$ , while all others are of type $A_1$ .

Assume now $\widehat {s}$ is not birational. By Proposition 5.4, $G/P$ is either $G_2/P_1$ or $F_4/P_3$ as $\varepsilon $ is divisorial. Consider first the case of $G_2/P_1$ , which is isomorphic to the five-dimensional quadric $\mathbb {Q}^5$ . Let $\mathcal {O}$ be the ten-dimensional nilpotent orbit in $\mathfrak {g}_2$ and $\mathcal {O}' \subset \mathfrak {so}_7$ the nilpotent orbit corresponding to the partition $[3, 1^4]$ . Then there is a generically 2-to-1 morphism $\nu : \overline {\mathcal {O}'} \to \overline {\mathcal {O}}$ , which is induced from the projection $\mathfrak {so}_7 \to \mathfrak {g}_2$ . The map $\widehat {s}: T^*_{G_2/P_1} \to \overline {\mathcal {O}}$ factorises through $\nu $ . As $\overline {\mathcal {O}'}$ is normal, we have $\widetilde {\mathcal {O}} = \overline {\mathcal {O}'}$ , which has generic singularity type $A_1$ .

Now consider the case of $F_4/P_3$ . In this case, the Springer map $\widehat {s}: T^*_{F_4/P_3} \to \overline {\mathcal {O}}_{F_4(a_3)}$ has degree 4 [10, Appendix]. By Theorem 1.3 in [11], the transverse slice $\mathcal {T}$ from the codimension 6 orbit $\mathcal {O}_{A_2+\tilde {A}_1}$ to $\overline {\mathcal {O}}_{F_4(a_3)}$ is isomorphic to the quotient $(\mathbb {C}^3 \oplus \mathbb {C}^{3*})/\mathfrak {S}_4$ , where $\mathfrak {S}_4$ acts on $\mathbb {C}^3$ by reflection representation. The only index 4 subgroup of $\mathfrak {S}_4$ is $\mathfrak {S}_3$ , hence, the degree 4 map $\widetilde {\tau }: \widetilde {\mathcal {O}} \to \overline {\mathcal {O}}_{F_4(a_3)}$ is locally the quotient $(\mathbb {C}^3 \oplus \mathbb {C}^{3*})/\mathfrak {S}_3 \to (\mathbb {C}^3 \oplus \mathbb {C}^{3*})/\mathfrak {S}_4$ . Hence, the generic singularity of $\widetilde {\mathcal {O}} $ is the same as that of $(\mathbb {C}^3 \oplus \mathbb {C}^{3*})/\mathfrak {S}_3$ , which is of type $A_1$ .

We can summarise the types of $G/P$ in the following table. By Proposition 5.9 and Corollary 5.10, we get the number $a, b$ for $G/P$ not of type (I) and (II-s), the latter cases will be done in the next subsection by applying Proposition 5.8.

As an immediate application, we obtain:

Proposition 5.14. Let $X=G/P$ be a rational homogeneous space of Picard number $1$ . Denote by H the ample generator of $\operatorname *{\mathrm {Pic}}(X)$ and by $\pi :\mathbb {P}(T_X)\rightarrow X$ the natural projection.

1. (1) If X is isomorphic to one of the varieties listed in Conjecture 1.2, then the normalised tangent bundle of X is pseudoeffective but not big.

2. (2) If X is a homogeneous Fano contact manifold different from a projective space, then the total dual VMRT $\check {{\mathcal C}}\subset \mathbb {P}(T_X)$ is a prime divisor satisfying:

   $$\begin{align*}[\check{{\mathcal C}}] \equiv 4\Lambda - 2\pi^*H. \end{align*}$$

Proof. For statement (1), this is already proved in [47]. Here, we use the total dual VMRT to give a new proof. In fact, this can be easily derived from the table below:

Note that the VMRT of X is not dual defective and its codegree is given in the last row of the table above. Moreover, by Proposition 5.13 and Corollary 5.10 we have:

$$\begin{align*}[\check{{\mathcal C}}] \equiv a \Lambda -2 \pi^*H. \end{align*}$$

Then one can easily check case by case that we have $a\cdot \text {index}(X)-2\cdot \dim (X)=0$ . Hence, the normalised tangent bundle of X is pseudoeffective but not big by Theorem 3.4.

For statement (2), it can be derived from the table below by the same argument as above:

Note that all the VMRTs above are not dual defective with codegree $4$ (see [50, p. 169]). In particular, by Proposition 5.13 and Corollary 5.10, we have $[\check {{\mathcal C}}]\equiv 4\Lambda - 2\pi ^*H$ .

5.D Geometry of stratified Mukai flops

This subsection is devoted to explicitly calculate the positive integers $a(H)$ and $b(H)$ in Proposition 5.8. It turns out that the flops are symmetric. In particular, according to Proposition 5.8, after exchanging $\mu $ and $\mu ^{-1}$ , we get $a(H)=\pi ^*_1 H \cdot \mu _*^{-1}(\ell _2)$ , and, hence, we always have $b(H)=1$ . It remains to determine $a(H)$ , which by Proposition 5.8 can be interpreted as the degree of the image under the flop of a general line in the projectivised cotangent space. We will describe in detail the flops which will enable us to determine this degree.

For a stratified Mukai flop $\widehat {\mu }: T^*_{G/P} \dashrightarrow T^*_{G/Q}$ (where P may coincide with Q), it induces a rational map $\nu : \mathbf {P}(T^*_{G/P,o}) \dashrightarrow G/Q$ by composing the projectivisation of $\widehat {\mu }$ with the projection $\mathbf {P}(T^*_{G/Q})\to G/Q$ . The aim of this section is to describe the rational map $\nu $ and then compute the degree of $\nu (\ell )$ for a general line $\ell $ in $\mathbf {P}(T^*_{G/P,o})$ . The result is summarised in the following table:

5.D.1 Preliminary

Recall that for a simple Lie algebra $\mathfrak {g}$ , there exist only finitely many nilpotent orbits in $\mathfrak {g}$ . In classical types, these orbits are parameterised by certain partitions, which correspond to sizes of the Jordan blocks in each conjugacy class.

Now we consider classical B-C-D types. Let $\epsilon \in \{0,1\}$ and V a d-dimensional vector space with a nondegenerate bilinear form, such that $\langle v, w \rangle = (-1)^{\epsilon } \langle w, v \rangle $ for all $v, w \in V$ .

Given a nilpotent element $\phi : V \to V$ preserving the bilinear form, we can associate to it a partition $\mathbf {d}=[d_1, \cdots , d_l]$ of d. Except a few cases in type D, this partition uniquely determines the conjugacy class of $\phi $ , denoted by $\mathcal {O}_{\mathbf {d}}$ .

We identify the partition $\mathbf {d}$ with a Young table consisting of d boxes, where the i-th row consists of $d_i$ boxes for each i. We denote by $(i,j)$ the box of $\mathbf {d}$ lying on the i-th column and j-th row. Let us recall the following classical result (cf. Proof of [39, Theorem 4.5]).

Proposition 5.15. For an element $\phi \in \mathcal {O}_{\mathbf {d}}$ , there exists a basis $e(i,j)$ of V indexed by the Young diagram $\mathbf {d}$ with the following properties:

1. (a) $\phi (e(i, j)) = e(i-1,j)$ for all $(i,j) \in \mathbf {d}$ .

2. (b) $\langle e(i, j), e(p, q)\rangle \neq 0 $ if and only if $p=d_j-i+1$ and $q=\beta (j)$ , where $\beta $ is a permutation of $\{1,2, \cdots , l\}$ (l is the length of the partition), which satisfies $\beta ^2=id$ , $d_{\beta (j)} = d_j$ and $\beta (j) \not \equiv j (\text {mod } 2)$ if $d_j \not \equiv \epsilon (\text {mod } 2)$ . One can choose an arbitrary $\beta $ within these restrictions.

We start with the following elementary result.

Proposition 5.16. Let $a < b$ be two integers and m an odd integer. Let $A, B, W$ be vector spaces of dimension $a, b, m$ , respectively.

1. (1) Consider the rational map $\nu _1: \mathbf {P}(\mathrm {Hom}(A, B)) \dashrightarrow \mathrm {Gr}(a, B)$ by sending a general element $\psi \in \mathrm {Hom}(A, B)$ to its image $\mathrm {Im}(\psi ) \subset B$ . Then $\nu _1$ sends a general line in $\mathbf {P}(\mathrm {Hom}(A, B))$ to a curve of degree a in $\mathrm {Gr}(a, B)$ .

2. (2) Consider the rational map $\nu _2: \mathbf {P}(\wedge ^2 W) \dashrightarrow \mathbf {P} W^*$ by sending a general element $\psi \in \wedge ^2 W$ to its kernel $\mathrm {Ker}(\psi )$ (by viewing $\psi $ as a map from $W^*$ to W). Then $\nu _2$ sends a general line in $\mathbf {P}(\wedge ^2 W)$ to a curve of degree $m-1$ in $\mathbf {P}(W^*)$ .

Proof. (1) Take a general (parameterised) line $[\psi _{\lambda }] \in \mathbf {P}(\mathrm {Hom}(A, B))$ (with $\lambda \in \mathbf {P}^1$ ), then $\psi _{\lambda }: A \to B$ is injective. Take a basis $e_1, \cdots , e_a$ of A, then $\mathrm {Im}(\psi _{\lambda }) \subset \mathrm {Gr}(a, B)$ corresponds to the curve (under the Plücker embedding):

$$ \begin{align*}\lambda \mapsto \psi_{\lambda}(e_1) \wedge \cdots \wedge \psi_{\lambda}(e_a),\end{align*} $$

which is of degree a as $\psi _{\lambda }$ is linear in $\lambda $ .

(2) For a general element $\psi \in \wedge ^2V$ , it has the maximal rank $m-1$ as m is odd. Take a general subspace $W_0^* \subset W^*$ of codimension 1, then $\psi : W_0^* \to \mathrm {Im}(\psi )$ is an isomorphism. By taking a basis of $W_0^*$ and using a similar argument as in (1), we see that $\nu _2$ maps a general line to a degree $m-1$ curve in $\mathrm {Gr}(m-1, W) \simeq \mathbf {P} W^*$ .

5.D.2 Type $A_{n,k}$

Let V be an $(n+1)$ -dimensional vector space and $k <(n+1)/2$ an integer. The $A_{n,k}$ flop is the birational map $\widehat {\mu }: T^*\mathrm {Gr}(k, V) \dashrightarrow T^* \mathrm {Gr}(k, V^*)$ , which is given as follows:

For any $[F] \in \mathrm {Gr}(k, V)$ , there exists a natural isomorphism $T_{[F]}^*\mathrm {Gr}(k, V) \simeq \mathrm {Hom}(V/F, F)$ . An element $\phi \in \mathrm {Hom}(V/F, F)$ gives naturally an element:

$$ \begin{align*} \phi^* \in \mathrm{Hom}(F^*, (V/F)^*) \subset \mathrm{Hom}(F^*, V^*). \end{align*} $$

If $\phi $ is general, then $\phi : V/F \to F$ is surjective as $\dim F < \dim V/F$ . This gives an injective map $\phi ^*: F^* \to (V/F)^*$ , whose image gives an element $[\mathrm {Im}(\phi ^*)] \in \mathrm {Gr}(k, (V/F)^*) \subset \mathrm {Gr}(k, V^*)$ . The flop $\widehat {\mu }$ sends $([F], \phi )$ to $([\mathrm {Im}(\phi ^*)], \phi ^*)$ . Hence, the rational map $\nu $ is given by:

$$ \begin{align*} \nu: \mathbf{P}(T^*_{[F]}\mathrm{Gr}(k, V)) \dashrightarrow \mathrm{Gr}(k, (V/F)^*) \subset \mathrm{Gr}(k, V^*), \quad [\phi] \mapsto [\mathrm{Im}(\phi^*)]. \end{align*} $$

By Proposition 5.16, $\nu $ maps a general line to a curve of degree k on $\mathrm {Gr}(k, V^*)$ .

5.D.3 Type $D_{2n+1}$

Let $(V, \langle , \rangle )$ be an orthogonal space of dimension $4n+2$ . The spinor variety $\mathbb {S}:=\mathbb {S}_{2n+1}$ , which parameterises $(2n+1)$ -dimensional isotropic subspaces of $(V, \langle , \rangle )$ , consists of two irreducible components $\mathbb {S}^+, \mathbb {S}^- $ . It turns out the Richardson orbits in $ \mathfrak {so}_{4n+2}$ associated to $\mathbb {S}^+$ and $ \mathbb {S}^- $ are the same, which corresponds to the partition $[2^{2n}, 1^2]$ . The two Springer maps $T^* \mathbb {S}^+ \xrightarrow {\widehat {s}^+} \overline {\mathcal {O}} \xleftarrow {\widehat {s}^-} T^*\mathbb {S}^-$ are birational, which gives the $D_{2n+1}$ flop $\widehat {\mu }: T^* \mathbb {S}^+ \dashrightarrow T^* \mathbb {S}^-$ .

The flop $\widehat {\mu }$ can be described as follows (cf. [39, Lemma 5.6]): given a general element $\phi \in \mathcal {O}$ , the kernel $\mathrm {Ker}(\phi )$ is of dimension $2n+2$ , which contains the two-dimensional vector subspace $\mathrm {Im}(\phi )$ . The quotient $\bar {V}:=\mathrm {Ker}(\phi )/\mathrm {Im}(\phi )$ is a two-dimensional orthogonal vector space, which has exactly two isotropic lines (say $L^+, L^-$ ). Then their preimages in $\mathrm {Ker}(\phi )$ give two $(2n+1)$ -dimensional isotropic subspaces $F^+, F^-$ of V. This gives two points $[F^{\pm }] \in \mathbb {S}^{\pm }$ . The flop $\mu $ maps $([F^+], \phi )$ to $([F^-], \phi )$ . Note that we have a natural isomorphism $F^-/\mathrm {Im}(\phi ) \simeq \mathrm {Ker}(\phi )/F^+$ , which shows that $F^-$ is the linear span of $\mathrm {Im}(\phi )$ and $\mathrm {Ker}(\phi )/F^+$ .

For an element $[F] \in \mathbb {S}^+$ , we have a natural isomorphism $V/F \simeq F^*$ induced from the pairing $\langle , \rangle $ on V as $F = F^{\perp }$ . Furthermore, $T_{[F]}^* \mathbb {S}^+ \simeq \wedge ^2 F$ . We fix a (noncanonical) isomorphism $V \simeq F \oplus F^*$ , such that the pairing $\langle , \rangle $ on V corresponds to the natural pairing on $F \oplus F^*$ .

For general $\phi \in \wedge ^2 F$ , its kernel is one-dimensional (as $\dim F$ is odd), which defines a point $[f_{\phi }^*] \in \mathbf {P}F^*$ . Then $\mathrm {Im}(\phi )$ is just the hyperplane $H_{\phi }$ in F annihilating $f_{\phi }^*=0$ . Thus, the rational map $\nu $ is the composition of maps:

$$ \begin{align*} \mathbf{P}(\wedge^2 F) \dashrightarrow \mathbf{P} F^* \subset \mathbb{S}^-, \quad [\phi] \mapsto [f_{\phi}^*] \mapsto <H_{\phi}, f_{\phi}^*>. \end{align*} $$

By Proposition 5.16, $\nu $ maps a general line in $\mathbf {P}(\wedge ^2 F)$ to a curve of degree $2n$ in the Plücker embedding of $\mathbb {S}^-$ .

Note that the composition $\mathbb {S}^- \subset \mathrm {Gr}(2n+1, V) \subset \mathbf {P} (\wedge ^{2n+1} V)$ is induced by $\mathcal {O}_{\mathbb {S}^-}(2)$ , hence, this gives a degree n curve on $\mathbb {S}^-$ .

5.D.4 Type $E_{6,I}$

Consider the $E_{6,I}$ flop $\widehat {\mu }: T^* (E_6/P_1) \dashrightarrow T^*(E_6/P_6)$ . Fix a point $o \in E_6/P_1$ , then the cotangent space $T_o^* (E_6/P_1)$ can be identified with the spinor representation $\mathcal {S}$ of $\mathrm {Spin}_{10}$ . Let $\mathbb {Q}^8$ be the smooth eight-dimensional hyperquadric. By [6, Proposition 1.5], there exists a unique $\mathbb {C}^* \times \mathrm { Spin}_{10}$ -equivariant rational map $\hat {\nu }: \mathcal {S} \dashrightarrow \mathbb {Q}^8$ , which is defined as follows: the affine cone of the ten-dimensional spinor variety $\hat {\mathbb {S}}_5 \subset \mathcal {S}$ is defined by ten quadratic equations $Q_1=\cdots =Q_{10}=0$ , and the map $\hat {\nu }$ is given by $z \mapsto [Q_1(z):\cdots :Q_{10}(z)] \in \mathbb {P}^{9}$ , whose image is contained in $\mathbb {Q}^8$ . This implies that if we take a general line $\ell $ in $\mathbb {P} \mathcal {S}$ , then $\nu (\ell )$ is a conic on $\mathbb {Q}^8$ .

By [6, Theorem 3.3], the map $\hat {\nu }$ is the composition of $\widehat {\mu }$ with the projection $T^* (E_6/P_6) \to E_6/P_6$ (under the natural embedding $\mathbb {Q}^8 \subset E_6/P_6$ ). This shows that the rational map $\nu : \mathbf {P} T_o^*(E_6/P_1) \dashrightarrow E_6/P_6$ maps a general line to a conic.

5.D.5 Type $E_{6, II}$

Let F be a five-dimensional vector space. By [6, Proposition 2.1], there exists a unique $\mathrm {GL}_2 \times \mathrm {GL}(F)$ -equivariant rational map:

$$ \begin{align*} g: \wedge^2 F^* \oplus \wedge^2 F^* \dashrightarrow \mathrm{Gr}(3, F), \end{align*} $$

which maps a general element $(\omega _1, \omega _2) \in \wedge ^2 F^* \oplus \wedge ^2 F^*$ to $\mathrm {Ker}(\omega _1)^{\perp _{\omega _2}} \cap \mathrm { Ker}(\omega _2)^{\perp _{\omega _1}}$ . Here, $\omega _i \in \wedge ^2 F^*$ is viewed as a two form on F and $\mathrm { Ker}(\omega _1)^{\perp _{\omega _2}}$ means the orthogonal space with respect to $\omega _2$ of the subspace $\mathrm {Ker}(\omega _1)$ . As $\omega _i$ is general, it has rank 4, hence, $\mathrm {Ker}(\omega _i)$ is one-dimensional, which shows that $\mathrm {Ker}(\omega _1)^{\perp _{\omega _2}} \cap \mathrm {Ker}(\omega _2)^{\perp _{\omega _1}}$ is a three-dimensional vector subspace in F. By [6, Lemma 2.3], we have $g(a \omega _1 + b \omega _2, a' \omega _1 + b' \omega _2) = g(\omega _1, \omega _2)$ for a general element $\begin {pmatrix} a & b \\ a' & b' \end {pmatrix}$ in $\mathrm {GL}_2$ . By [6, Lemma 2.4], a general element $\phi =(\omega _1, \omega _2) \in \wedge ^2 F^* \oplus \wedge ^2 F^*$ can be codiagonalised as follows (under a suitable basis $f_1^*, \cdots , f_5^*$ of F):

$$ \begin{align*} \omega_1 = f_2^* \wedge f_4^* + f_3^* \wedge f_5^*, \qquad \omega_2 = f_1^* \wedge f_5^* + f_3^* \wedge f_4^*. \end{align*} $$

Take another element $\phi '=(\omega ^{\prime }_1, \omega ^{\prime }_2)$ defined as follows:

$$ \begin{align*} \omega^{\prime}_1 = f_1^* \wedge f_4^* + f_3^* \wedge f_5^*, \qquad \omega^{\prime}_2 = f_1^* \wedge f_2^* + f_3^* \wedge f_4^*. \end{align*} $$

Consider the following plane in $\wedge ^2 F^* \oplus \wedge ^2 F^*$ given by $\phi _{s,t} = s \phi + t \phi ' =(\omega _1^{s,t}, \omega _2^{s,t})$ for $(s,t) \in \mathbb {C}^2$ . By a direct computation, we have:

$$ \begin{align*} \mathrm{Ker}(\omega_1^{s,t}) = \mathbb{C} (sf_1 - t f_2), \qquad \mathrm{Ker}(\omega_2^{s,t}) = \mathbb{C} (sf_2 - t f_5). \end{align*} $$

One remarks that for any $(s, t) \neq (0,0)$ , the subspaces $\mathrm {Ker}(\omega _1^{s,t})$ and $\mathrm {Ker}(\omega _2^{s,t})$ are pne-dimensional and they intersect only at $(0,0)$ . Moreover, one shows directly that:

$$ \begin{align*} \omega_2(\mathrm{Ker}(\omega_1^{s,t}), \cdot) \cap \omega_1(\mathrm{Ker}(\omega_2^{s,t}), \cdot) =\{0\}. \end{align*} $$

This shows that $g(\phi _{s,t})$ is well defined for $(s,t) \neq (0,0)$ . By a direct computation, we have:

$$ \begin{align*} g(\phi_{s,t}) = \left\{ \sum_i x_i f_i | x_5 = \frac{t^2}{s^2} x_1 - \frac{t}{s} x_2, x_4 = \frac{(s+t)t}{s^2} x_3\right\}. \end{align*} $$

This gives a basis for $g(\phi _{s,t})$ , which, under the Plücker embedding is mapped to the following curve on $\mathrm {Gr}(3, F)$ :

$$ \begin{align*} [s:t] \mapsto [(f_1 + \frac{t^2}{s^2} f_5) \wedge (f_2 - \frac{t}{s} f_5) \wedge (f_3 + \frac{(s+t)t}{s^2} f_4)]. \end{align*} $$

Note that this gives a degree 4 curve on $\mathrm {Gr}(3, F)$ .

Consider the $E_{6,II}$ flop $\widehat {\mu }: T^*(E_6/P_3) \dashrightarrow T^*(E_6/P_5)$ . By [6, Theorem 4.3], the composition $T_o^*(E_6/P_3) \dashrightarrow T^*(E_6/P_5) \to E_6/P_5$ can be identified with the composition of g with the natural embedding $\mathrm {Gr}(3, F) \subset E_6/P_5$ . The precedent argument shows that a general line in $\mathbf {P} T_o^*(E_6/P_3)$ is mapped to a degree 4 curve on $E_6/P_5$ .

5.D.6 Type $B_{n, k}$

Let $(V, \langle , \rangle )$ be an orthogonal space of dimension $2n+1$ . A vector subspace $F \subset V$ is said orthogonal if $F \subset F^{\perp }$ . The k-th orthogonal Grassmann variety $B_n/P_k$ parameterises k-dimensional orthogonal vector subspaces in V. There exists an isomorphism:

$$ \begin{align*}T^*(B_n/P_k) \simeq \{([F], \phi) \in B_n/P_k \times \mathfrak{so}(V)| \phi(V) \subset F^{\perp}, \phi(F^{\perp}) \subset F \subset \mathrm{Ker}(\phi) \}. \end{align*} $$

Under this isomorphism, the Springer map $\widehat {s}: T^* (B_n/P_k) \to \overline { \mathcal {O}}_{\mathbf {d}}$ sends $([F], \phi )$ to $\phi $ .

When k is even, such that $k> \frac {2n+1}{3}$ , the Springer map $\pi $ is generically finite of degree 2 and $\mathbf {d} = [3^{2n+1-2k}, 2^{3k-2n-2}, 1^2]$ . The involution on general fibres of $\pi $ gives the $B_{n, k}$ -flop: $\widehat {\mu }: T^*(B_n/P_k) \dashrightarrow T^*(B_n/P_k)$ .

For $\phi \in \mathcal {O}_{\mathbf {d}}$ , we choose a basis $e(i, j)$ of V as described by Proposition 5.15 (by taking $\beta $ satisfying $\beta (k)=k+1$ ). Then $\mathrm {Ker}(\phi )$ has dimension $k+1$ and is generated by $e(1,1), e(1, 2), \cdots , e(1, k+1)$ . The two fibres $\pi ^{-1}(\phi )$ are given by the following two orthogonal subspaces (cf. Proof of [39, Theorem 4.5]):

$$ \begin{align*} F_1 = \sum_{1 \leq j \leq k} \mathbb{C} e(1, j) \ \text{and } F_2 = \sum_{1 \leq j \leq k-1} \mathbb{C} e(1, j) + \mathbb{C} e(1, k+1). \end{align*} $$

One notes that $F_0:=F_1 \cap F_2 = F_1 \cap \mathrm {Im}(\phi ) =\mathrm {Im}(\phi ) \cap \mathrm {Ker}(\phi )$ is of dimension $k-1$ and $F_2/F_0$ is naturally isomorphic to $\mathrm {Ker}(\phi )/F_1$ . The flop $\widehat {\mu }$ interchanges the two fibres. Namely, the flop $\widehat {\mu }$ sends $([F_1], \phi )$ to $([F_2], \phi )$ , where $F_2$ is the linear span of $F_1 \cap \mathrm {Im}(\phi )$ and $\mathrm {Ker}(\phi )/F_1$ , the latter being one-dimensional. Furthermore, $\langle \mathrm { Ker}(\phi )/F_1, F_0 \rangle =0$ and as $F_0 \subset F_1$ is a hyperplane, it is exactly the orthogonal part in F of $\mathrm {Ker}(\phi )/F_1$ . This implies that $F_2$ is in fact uniquely determined by $\mathrm {Ker}(\phi )/F_1$ . We summarise these in the following picture on Young table.

Fix an orthogonal space $[F] \in B_n/P_k$ , then $F^{\perp }/F$ is an orthogonal space of dimension $2n+1-2k$ and $V/F^{\perp }$ is isomorphic to $F^*$ via the pairing $F \times V/F^{\perp } \to \mathbb {C}$ induced from the bilinear form on V. We fix a (noncanonical) isomorphism $V \simeq F \oplus F^* \oplus F^{\perp }/F$ , such that the orthogonal form on V is given by that induced on $F^{\perp }/F$ and the natural one on $F \oplus F^*$ .

By [26, Proposition 5.1], we have:

$$ \begin{align*} \iota_F: T_{[F]}^* (B_n/P_k) \simeq \mathrm{Hom}(F^{\perp}/F, F) \oplus \wedge^2 F. \end{align*} $$

This isomorphism is given as follows: for $\phi \in T_{[F]}^* (B_n/P_k)$ , it induces a map $\phi _0 \in \mathrm {Hom}(F^{\perp }/F, F) $ as $F \subset \mathrm {Ker}(\phi )$ and $\phi (F^{\perp }) \subset F$ . As $\phi (V) \subset F^{\perp }$ , it induces a map $(\phi _1, \phi _2): V/F^{\perp } \to F^{\perp }/F \oplus F$ . It turns out that $\phi \in \mathfrak {so}(V)$ is equivalent to the following: (1) the map $\phi _1: V/F^{\perp } \simeq F^* \to F^{\perp }/F$ is the dual $-\phi _0^*$ of the map $-\phi _0$ (here, $F^{\perp }/F$ is self-dual) and (2) the map $\phi _2: V/F^{\perp } \simeq F^* \to F$ is in fact an element in $\wedge ^2 F$ . Then the isomorphism $\iota _F$ sends $\phi $ to $(\phi _0, \phi _2)$ .

Conversely, given $(\phi _0, \phi _2) \in \mathrm {Hom}(F^{\perp }/F, F) \oplus \wedge ^2 F$ , we construct $\bar {\phi }$ as a map from $V/F \simeq V/F^{\perp } \oplus F^{\perp }/F$ to $F \oplus F^{\perp }/F $ , which is given as follows:

$$ \begin{align*} \bar{\phi} = \begin{pmatrix} \phi_2 & \phi_0 \\ -\phi_0^* & 0 \end{pmatrix}. \end{align*} $$

Thus, $\bar {\phi }$ is represented as an antisymmetric matrix of size $\dim V/F = 2n+1-k$ . Note that $\dim V/F$ is odd as k is even, so for a general choice of $(\phi _0, \phi _2)$ , the map $\bar {\phi }$ is of maximal rank $2n-k$ and $\mathrm {Ker}(\bar {\phi })$ is one-dimensional. Note that $\mathrm {Ker}(\bar {\phi }) = \mathrm {Ker}(\phi )/F$ . By the natural quotient $V/F \to V/F^{\perp } \simeq F^*$ , the image of $\mathrm {Ker}(\bar {\phi })$ gives a line $\mathbb {C} f^* \subset F^*$ . Then the flop $\mu $ maps $([F], \phi )$ to $([F'], \phi )$ , where $F' \subset F \oplus F^* \subset V$ is the subspace generated by $H_{f^*}$ and $f^*$ , here, $H_{f^*}$ is the hyperplane in F defined by $f^*=0$ . Then the map is then given by $[\phi _0, \phi _1] \mapsto [F']$ .

Note that $H_{f^*}$ is uniquely determined by $f^*$ , while $f^*$ is given by the kernel $\mathrm {Ker}(\bar {\phi }^*)$ . By Proposition 5.16, $\nu $ maps a line to a curve of degree $2n-k$ on $B_n/P_k$ for the Plücker embedding of $B_n/P_k$ . Thus, for $k \neq n$ , this gives a degree $2n-k$ curve on $B_n/P_k$ , while for $k=n$ , this gives a curve of degree $n/2$ on $B_n/P_n$ as $B_n/P_n \subset \mathrm {Gr}(n, 2n+1) \subset \mathbb {P}^N$ is induced by $\mathcal {O}(2)$ .

Remark 5.17. By [40, Example 3.3], $B_{2n, 2n}$ -flop is the same as $D_{2n+1}$ -flop. Hence, we recover the result in Section 5.D.3.

5.D.7 Type $D_{n, k}$

Let $(V, \langle , \rangle )$ be an orthogonal space of dimension $2n$ . As in the $B_{n, k}$ -flop case, we have the following isomorphism of the cotangent bundle of the k-th orthogonal Grassmann variety $D_n/P_k$ :

$$ \begin{align*}T^*(D_n/P_k) \simeq \{([F], \phi) \in D_n/P_k \times \mathfrak{so}(V)| \phi(V) \subset F^{\perp}, \phi(F^{\perp}) \subset F \subset \mathrm{Ker}(\phi) \}. \end{align*} $$

Under this isomorphism, the Springer map $\widehat {s}: T^* (B_n/P_k) \to \overline { \mathcal {O}}_{\mathbf {d}}$ sends $([F], \phi )$ to $\phi $ .

When k is odd, such that $n-2 \geq k> \frac {2n}{3}$ , the Springer map $\widehat {s}$ is generically finite of degree 2 and $\mathbf {d} = [3^{2n-2k}, 2^{3k-2n-1}, 1^2]$ . The involution on the general fibres of $\widehat {s}$ gives the $D_{n, k}$ -flop: $\widehat {\mu }: T^*(D_n/P_k) \dashrightarrow T^*(D_n/P_k)$ .

This flop is similar to the $B_{n, k}$ -flop. By the similar argument, we see that a general line in $\mathbf {P} (T^*_{[F]} (D_n/P_k))$ is mapped to a curve of degree $2n-k-1$ .

5.D.8 Type $C_{n, k}$

Let $(V, \omega )$ be a symplectic vector space of dimension $2n$ . A vector subspace $F \subset V$ is said isotropic if $F \subset F^{\perp }$ . The k-th symplectic Grassmann variety $C_n/P_k$ parameterises k-dimensional isotropic vector subspaces in V. There exists an isomorphism:

$$ \begin{align*} T^*(C_n/P_k) \simeq \{([F], \phi) \in C_n/P_k \times \mathfrak{sp}(V)| \phi(V) \subset F^{\perp}, \phi(F^{\perp}) \subset F \subset \mathrm{Ker}(\phi) \}. \end{align*} $$

Under this isomorphism, the Springer map $\widehat {s}: T^* (C_n/P_k) \to \overline { \mathcal {O}}_{\mathbf {d}}$ sends $([F], \phi )$ to $\phi $ .

When k is odd, such that $k \leq \frac {2n}{3}$ , the Springer map $\pi $ is generically finite of degree 2 and $\mathbf {d} = [3^{k-1}, 2^{2}, 1^{2n-3k-1}]$ . The involution on the general fibres of $\pi $ gives the $C_{n, k}$ -flop: $\widehat {\mu }: T^*(C_n/P_k) \dashrightarrow T^*(C_n/P_k)$ .

When $k=1$ , then $\mathbf {d} = [2^{2}, 1^{2n-4}]$ and an element $\phi \in \mathcal {O}_{\mathbf {d}}$ has rank 2, so $\mathrm {Im}(\phi )$ is two dimensional. The flop $\mu $ sends $([F], \phi )$ to $([\mathrm {Im}(\phi )/F], \phi )$ . In this case, if we take a general pencil $\phi _{\lambda } \in T_{[F]}^* (C_n/P_1)$ , then the flop $\widehat {\mu }$ maps it to a line in $C_n/P_1$ .

Now we consider the case $3 \leq k \leq \frac {2n}{3}$ . Fix $[F] \in C_n/P_k$ and take a general pencil $\phi _{\lambda } \in T^*_{[F]}(C_n/P_k)$ . Note that $\phi _{\lambda }^2=\phi _{\lambda } \circ \phi _{\lambda }$ has rank $k-1$ , hence, $\mathrm {Im}( \phi _{\lambda }^2)$ is a vector subspace of dimension $k-1$ in F. It defines an element $f_{\lambda }^*$ in $F^* \simeq V/F^{\perp }$ , which is unique up to a scalar. Then the image of $([F], \phi _{\lambda })$ under the flop $\widehat {\mu }$ is $([F_{\lambda }], \phi _{\lambda })$ , where $F_{\lambda }$ is spanned by $\mathrm {Im}( \phi _{\lambda }^2)$ and $f_{\lambda }^*$ . This gives a curve on $C_n/P_k$ , which is given in the Plücker embedding $\phi _{\lambda }^2(v_1) \wedge \phi _{\lambda }^2(v_2) \cdots \wedge \phi _{\lambda }^2(v_{k-1})$ for general chosen $k-1$ vectors $v_1, \cdots , v_{k-1}$ of V, as $\phi _{\lambda }^2$ is quadratic in $\lambda $ . This gives a curve of degree $2(k-1)$ .

5.E Proof of Theorem 1.14

If the morphism $\varepsilon : \mathbf {P}(T^*_{G/P})\rightarrow \mathbf {P}(\widetilde {{\mathcal O}})$ is a divisorial contraction, then Proposition 5.9 and Corollary 5.10 can be applied to determine a and b. Nevertheless, in general, it is not easy to compute the Segre classes $\Lambda ^{2n-1}$ and $\Lambda ^{2n-1}\cdot \pi ^*H$ . In the following, we shall use a similar method as the previous subsection to determine a and b in the classical cases. We start with the following result which computes the pseudoeffective threshold for $G/P$ of type (II-d-d).

Proposition 5.18. Let $G/P$ be a rational homogeneous space of type (II-d-d) of classical type. Then the pseudoeffective threshold of $G/P$ is given by $\alpha _{G/P} = 1/a$ , where a is the integer given by the following table.

Proof. Note that for $G/P$ of type (II-d-d), the Springer map $\widehat {s}: T_{G/P}^* \to \overline {\mathcal {O}}$ is birational by Proposition 5.4. Let $\Gamma $ be the exceptional divisor, and write $[\Gamma ] \equiv a(\Gamma ) \Lambda - b(\Gamma ) \pi ^*H$ . By Corollary 5.10, we have $b(\Gamma )=1$ . By Theorem 5.5, we have $\alpha _{G/P} = 1/a(\Gamma )$ . By Proposition 5.9, we have $a(\Gamma )\Lambda ' \equiv H'$ , which can be used to determine $a(\Gamma )$ for the classical cases.

As $\mathbf {P}(T_{G/P}^*) \to \mathbf {P}( \overline {\mathcal {O}})$ is birational, this gives a rational map . For any point $x \in \mathcal {O}$ , there exists an $\mathfrak {sl}_2$ -triplet $(x, y, h)$ by the Jacobson-Morozov theorem. The nilpotent elements in this $\mathfrak {sl}_2$ give a conic C on $\mathbf {P}(\mathcal {O})$ passing through $[x]$ . In other words, $\mathbf {P}(\mathcal {O})$ is covered by conics. Now we show that $\eta : C \to \eta (C)$ is birational: let $\mathfrak {n} \subset \mathfrak {g}$ be the nilradical of $\mathfrak {p}$ , which is naturally identified with $T_{G/P,o}^*$ . As $\mathcal {O}$ is Richardson, the intersection $\mathfrak {n} \cap \mathcal {O}$ is dense in $\mathfrak {n}$ , thus, $\mathfrak {n} \subset \overline {\mathcal {O}}$ . This implies that fibres of $T^*_{G/P} \to G/P$ are mapped to linear subspaces in $\overline {\mathcal {O}}$ . For any $y \in G/P$ , denote by $\mathfrak {n}_y$ this linear subspace. Then $\mathbf {P} (\mathfrak {n}_y) \cap C = \mathbf {P} (\mathfrak {n}_y) \cap \mathbf {P} (\mathfrak {sl}_2) \subset C$ . As C is a conic, while $\mathbf {P} (\mathfrak {n}_y) \cap \mathbf {P} (\mathfrak {sl}_2)$ is linear, we have $\mathbf {P} (\mathfrak {n}_y) \cap \mathbf {P} (\mathfrak {sl}_2)$ is just a point, which shows $\eta : C \to \eta (C)$ is birational. It follows that $a(\Gamma ) = \frac {\eta _*(C) \cdot H}{2}$ . Thus, we only need to compute the degree of the curve $\eta _*(C)$ .

Consider the case of $B_n/P_k$ with k odd and $k\geq \frac {2n+1}{3}$ . Then $\mathcal {O}$ corresponds to the partition $[3^{2n+1-2k}, 2^{3k-2n-1}]$ . Take an element $\phi \in \mathcal {O} \subset \mathfrak {so}(V)$ , then $\mathrm {Ker}(\phi )$ has dimension k as $\mathrm {rk}(\phi ) = 2n+1-k$ . Using the identification:

$$ \begin{align*}T^*(B_n/P_k) \simeq \{([F], \phi) \in B_n/P_k \times \mathfrak{so}(V)| \phi(V) \subset F^{\perp}, \phi(F^{\perp}) \subset F \subset \mathrm{Ker}(\phi) \}, \end{align*} $$

it follows that the map $\eta $ is given by $\eta (\phi ) = [\mathrm {Ker}(\phi )]$ . By Proposition 5.16, $\eta _*(C)$ is a curve of degree $2(2n+1-k)$ , which gives $a = 2n+1-k$ . The case of $D_n/P_k$ is completely similar.

Consider $C_n/P_k$ with k even and $k\leq \frac {2n}{3}$ . The nilpotent orbit $\mathcal {O}$ corresponds to the partition $[3^{k}, 1^{2n-3k}]$ . Take an element $\phi \in \mathcal {O}$ , then it is easy to see that $\eta (\phi ) = [\mathrm {Im}(\phi ^2)]$ . This shows that $\eta (C)$ is a curve of degree $4k$ , hence, $a=2k$ .

There are five $G/P$ of type (II-d-d) in exceptional Lie algebras. Although the similar approach works, the map $\eta $ is not explicit, which prevents us from doing the computation. In a similar way, we can get the following:

Lemma 5.19. The pseudoeffective threshold of $C_n/P_k$ with $k \geq \frac {2n+1}{3}$ is $\frac {2}{2n-k}$ .

Proof. Note that $C_n/P_k$ with $k \geq \frac {2n+1}{3}$ is of type (II-d-A1) and the Springer map $\widehat {s}: T_{C_n/P_k}^* \to \overline {\mathcal {O}}_{[3^{2n-2k},2^{3k-2n}]}$ is birational by Proposition 5.4. Let $\Gamma $ be the exceptional divisor, and write $[\Gamma ] \equiv a(\Gamma ) \Lambda - b(\Gamma ) \pi ^*H$ . By Corollary 5.10, we have $b(\Gamma )=2$ . By Theorem 5.5, we have $\alpha _{C_n/P_k} = 2/a(\Gamma )$ . To compute $a(\Gamma )$ , we consider the rational map:

As in the proof of Proposition 5.18, take a conic curve C on $\mathbf {P}(\mathcal {O})$ , then its image $\eta (C)$ is a curve of degree $2(2n-k)$ . This gives $a(\Gamma ) = 2n-k$ .

Now we are ready to prove our main result.

Proof of Theorem 1.14

The statement (1) is a direct consequence of Theorem 5.5 and Propositions 5.8 and 5.9.

For statement (2), let r and d be two positive integers. Then there exists an effective divisor $D\subset \mathbb {P}(T_{G/P})$ , such that $D\sim r\Lambda - d\pi ^*H$ if and only if:

$$\begin{align*}H^0(G/P,(\mathrm{Sym}^r T_{G/P})\otimes {\mathcal O}_{G/P}(-dH))\not=0. \end{align*}$$

First, we assume that the morphism $\varepsilon :\mathbf {P}(T^*_{G/P})\rightarrow \mathbf {P}(\widetilde {{\mathcal O}})$ is divisorial with exceptional divisor $\Gamma $ . Then $\Gamma $ is dominated by curves with $\Lambda $ -degree $0$ and $\Gamma \equiv a\Lambda - b\pi ^*H$ by our definition of a and b. Let m be the multiplicity of D along $\Gamma $ . Then the restriction of the following effective divisor:

$$\begin{align*}D-m\Gamma \equiv (r-am)\Lambda + (bm-d)\pi^*H \end{align*}$$

to $\Gamma $ is pseudoeffective. Then we obtain $r-am\geq 0$ and $bm-d\geq 0$ . This yields:

$$\begin{align*}d\leq bm \leq b\left\lfloor \frac{r}{a} \right\rfloor, \end{align*}$$

where the second inequality follows from the fact that m is an integer. Conversely, if r and d are two positive integers satisfying $ d\leq b\lfloor \frac {r}{a} \rfloor $ , we define $m=\lfloor \frac {r}{a}\rfloor $ , then we get:

$$\begin{align*}r\Lambda - d\pi^*H \sim m\Gamma + (r-am)\Lambda + (bm-d)\pi^*H. \end{align*}$$

Note that $r-am\geq 0$ and $bm-d\geq 0$ by our assumption. As $\Lambda $ and H are globally generated, it follows that there exists an effective divisor $D'$ , such that:

$$\begin{align*}r\Lambda - d\pi^*H\sim m\Gamma + D'\geq 0. \end{align*}$$

Next, we assume that the morphism $\varepsilon :\mathbf {P}(T^*_{G/P})\rightarrow \mathbf {P}(\widetilde {{\mathcal O}})$ is small. We consider the stratified Mukai flop $\mu :\mathbf {P}(T^*_{G/P})\dashrightarrow \mathbf {P}(T^*_{G/Q})$ . Let $D\subset \mathbf {P}(T^*_{G/P})$ be an effective divisor, such that:

$$\begin{align*}D\sim r\Lambda - d\pi_1^*H. \end{align*}$$

By Proposition 5.8, the push forward by $\mu $ shows:

$$\begin{align*}\mu_*D \sim r\Lambda' - d\mu_* \pi_1^*H \sim r\Lambda' - d( a\Lambda' - \pi_2^*H) \sim (r-da)\Lambda' + d\pi_2^*H, \end{align*}$$

where $\Lambda '$ is the tautological divisor of $\mathbf {P}(T^*_{G/Q})$ , and we use the fact that $b=1$ in this case. As $\mu _*D$ is effective, we obtain $r-da\geq 0$ . Conversely, if r and d are two positive integers satisfying $ d\leq b\lfloor \frac {r}{a} \rfloor $ , then we get $ad\leq r$ as $b=1$ . In particular, as $\Lambda '$ and H are globally generated, there exists an effective divisor $D'$ , such that $D'\sim (r-ad)\Lambda ' + d\pi _2^*H$ . Then the pull back $\mu ^*D'$ is an effective divisor, such that:

$$\begin{align*}\mu^*D' \sim (r-ad)\Lambda + d\mu^*\pi_2^*H \sim r\Lambda - d\pi_1^*H. \end{align*}$$

For statement (3), note first that the tangent bundle $T_{G/P}$ is semistable. Thus, by Lemma 2.8, we have:

$$\begin{align*}\frac{b}{a} = \alpha_{G/P} = \mathrm{index}(G/P) \cdot \alpha(G/P,-K_{G/P}) \leq \frac{\mathrm{index}(G/P)}{\dim(G/P)}. \end{align*}$$

In particular, the normalised tangent bundle of $G/P$ is pseudoeffective if and only if:

$$\begin{align*}a\cdot \mathrm{index}(G/P)= b \cdot \dim(G/P). \end{align*}$$

Consequently, as $b\leq 2$ , it follows that $2\dim (G/P)$ is divided by $\mathrm {index}(G/P)$ . Thus, for G of exceptional type, one can check by Appendix A that the normalised tangent bundle of $G/P$ is pseudoeffective if and only if $G/P$ is isomorphic to either $E_7/P_7$ or $G_2/P_1=\mathbb {Q}^5$ .

Type $A_n/P_k$ . Note that $A_n/P_k$ is isomorphic to $A_n/P_{n+1-k}$ . Thus, we may assume that $2k\leq n+1$ . First, we assume that $2k\leq n$ , then $a=k$ and $b=1$ . Then we have:

$$ \begin{align*} a\cdot \text{index}(A_n/P_k) - b\cdot \dim(A_n/P_k) = k(n+1) - k(n-k+1) = k^2>0. \end{align*} $$

Hence, the normalised tangent bundle of $A_n/P_k$ is not pseudoeffective if $2k\not = n+1$ . Next we assume that $2k=n+1$ , then we have $a=k$ and $b=2$ , and we have:

$$\begin{align*}a\cdot \text{index}(A_{n}/P_{k}) - b\cdot \dim(A_n/P_k) = k(n+1) - 2k(n-k+1) = k(2k-n-1) =0. \end{align*}$$

Hence, the normalised tangent bundle of $X=A_n/P_k$ is pseudoeffective if $2k=n+1$ and X is isomorphic to the Grassmann variety $\mathrm { Gr}(k,2k)$ in this case.

Type $B_n/P_k$ . First, we assume that $3k\leq 2n$ . Then $a=2k$ and $b=2$ . In particular, we have:

$$ \begin{align*} a\cdot \text{index}(B_n/P_k) - b\cdot \dim(B_n/P_k) = 2k(2n-k) - k(4n-3k+1) = k(k-1) \geq 0 \ \end{align*} $$

with equality if and only if $k=1$ . Hence, if $3k\leq 2n$ , then the normalised tangent bundle of $B_n/P_k$ is pseudoeffective if and only if $k=1$ , in which case, $B_n/P_k$ is isomorphic to the $(2n-1)$ -dimensional quadric ${\mathbb Q}^{2n-1}$ . Next, we assume that $2n+1\leq 3k\leq 3(n-1)$ . Then $a=2n-k$ (k even) or $2n-k+1$ (k odd), and $b=1$ . Nevertheless, note that we have:

$$ \begin{align*} 2a\cdot \text{index}(B_n/P_k) - 2b\cdot \dim(B_n/P_k) & \geq 2(2n-k)^2 - k(4n-3k+1) \\ & = 8n^2-12nk +5k^2 -k \\ & = (2n-2k)(4n-2k) + k^2-k>0. \end{align*} $$

Therefore, if $2n+1\leq 3k\leq 3(n-1)$ , then the normalised tangent bundle of $B_n/P_k$ is not pseudoeffective. Finally, we assume that $k=n$ . Then $a=\lfloor \frac {n+1}{2}\rfloor $ , and $b=1$ (n even) or $b=2$ (n odd). On the other hand, note that $B_n/P_n$ is the $\frac {n(n+1)}{2}$ -dimensional spinor variety $\mathbb {S}_{n+1}$ with index $2n$ . In particular, one can easily obtain that the normalised tangent bundle of $B_n/P_n$ is pseudoeffective if and only if n is odd.

Type $C_n/P_k$ . If $k=1$ , then $C_n/P_1$ is isomorphic to $\mathbb {P}^{2n-1}$ whose normalised tangent bundle is known to be nonpseudoeffective. Now we assume that $6\leq 3k\leq 2n$ , then $a=2k-2$ (k odd) or $a=2k$ (k even) and $b=1$ . If $k\geq 3$ , then we have:

$$ \begin{align*} 2a\cdot \text{index}(C_n/P_k) - 2b\cdot \dim(C_n/P_k) & \geq 2(2k-2)(2n-k+1) - k (4n-3k+1) \\ & = 4nk-k^2+7k-8n-4 \\ & =\frac{2nk}{3}-k^2 + \frac{10nk}{3} - 8n +7k-4>0. \end{align*} $$

Hence, the normalised tangent bundle of $B_n/P_k$ is not pseudoeffective if $9\leq 3k\leq 2n$ . For $k=2$ and $n \geq 3$ , one can easily check that the normalised tangent bundle of $B_n/P_2$ is not pseudoeffective in the same way. Finally, we assume that $3k\geq 2n+1$ . Then $a=2n-k$ and $b=2$ . Then we obtain:

$$ \begin{align*} a\cdot \text{index}(C_n/P_k) - b\cdot \dim(C_n/P_k) & = (2n-k)(2n-k+1) - k(4n-3k+1) \\ & \geq (2n-2k+1)(2n-2k) \geq 0 \end{align*} $$

with equality if and only if $k=n$ . In particular, if $3k\geq 2n+1$ , then the normalised tangent bundle of $C_n/P_k$ is pseudoeffective if and only if $k=n$ , which is the Lagrangian Grassmann variety $\mathrm LG(n,2n)$ .

Type $D_n/P_k$ . First, we assume that $3k\leq 2n-1$ . Then $a=2k$ and $b=2$ . Then we obtain:

$$ \begin{align*} a\cdot \text{index}(D_n/P_k) - b\cdot \dim(D_n/P_k) = 2k(2n-k-1) - k(4n-3k-1) \geq k^2 -k \geq 0, \end{align*} $$

with equality if and only if $k=1$ . Hence, if $3k\leq 2n-1$ , then the normalised tangent bundle of $D_n/P_k$ is pseudoeffective if and only if $k=1$ , which is the $(2n-2)$ -dimensional quadric ${\mathbb Q}^{2n-2}$ . Next, we assume that $2n\leq 3k\leq 3(n-2)$ , then $a=2n-k-1$ (k odd) or $a=2n-k$ (k even), and $b=1$ . In particular, we have:

$$ \begin{align*} 2a\cdot \text{index}(D_n/P_k) - 2b\cdot \dim(D_n/P_k) & \geq 2(2n-k-1)^2 - k(4n-3k-1) \\ & = 8n^2-12nk+5k^2+5k-8n+2 \\ & = (2n-2k)(4n-2k)+k^2+5k-8n+2 \\ & \geq 4(2n+4) + k^2+5k-8n+2> 0, \end{align*} $$

where the fourth inequality follows from the fact that $k\leq n-2$ . Hence, the normalised tangent bundle is not pseudoeffective if $2n\leq 3k\leq 3(n-2)$ . Finally, if $k\geq n-1$ , then $D_n/P_k$ is isomorphic to the spinor variety $\mathbb {S}_{n}=B_{n-1}/P_{n-1}$ and the normalised tangent bundle of $D_n/P_k$ with $k\geq n-1$ is pseudoeffective if and only if n is even.

6 Two nonhomogeneous examples

As mentioned in the Introduction, besides rational homogeneous spaces, there are only two known examples of Fano manifolds with Picard number $1$ and big tangent bundle: the del Pezzo threefold $V_5$ of degree $5$ and the horospherical $G_2$ -variety $\mathbb {X}$ . In this subsection, we describe the pseudoeffective cones of the projectivised tangent bundle of $V_5$ and $\mathbb {X}$ . Recall that $V_5$ is actually a codimension $3$ linear section of $\mathrm {Gr}(2,5)\subset \mathbb {P}^9$ and the bigness of $T_{V_5}$ is proved in [15] using the total dual VMRT. In particular, this gives the pseudoeffective cone of $\mathbb {P}(T_{V_5})$ by applying Theorem 3.4. Actually, we have the following complete descriptions of the cones of divisors of $\mathbb {P}(T_{V_5})$ .

Proposition 6.1. Let X be the del Pezzo Fano threefold $V_5$ of degree $5$ . Denote by $\pi :{\mathcal X}:=\mathbb {P}(T_X)\rightarrow X$ the projectivised tangent bundle of X. Let H be the ample generator of $\operatorname *{\mathrm {Pic}}(X)$ , and let $\Lambda $ be the tautological divisor of $\mathbb {P}(T_X)$ . Then we have:

$$\begin{align*}\begin{cases} \ \,\mathrm{Eff}({\mathcal X})=\left\langle3\Lambda-\pi^*H,\pi^*H \right\rangle \\ \mathrm{Mov}({\mathcal X}) =\left\langle \Lambda,\pi^*H\right\rangle \\ \ \mathrm{Nef}({\mathcal X})=\left\langle \Lambda+\pi^*H,\pi^*H\right\rangle. \end{cases} \end{align*}$$

In particular, the cones of divisors $\mathrm {Eff}({\mathcal X})$ , $\mathrm {Mov}({\mathcal X})$ and $\mathrm {Nef}({\mathcal X})$ are closed rational cones in $N^1({\mathcal X})$ .

Proof. The description of the effective cone $\mathrm {Eff}({\mathcal X})$ of ${\mathcal X}$ follows from Theorem 3.4 and [15, Theorem 5.4].

Note that $\check {{\mathcal C}}$ is dominated by curves with $\Lambda $ -degree $0$ . It follows that $\check {{\mathcal C}}\subset {\mathbb B}_+(\Lambda )$ . In particular, by Lemma 2.3 that $[\Lambda ]$ is not contained in the interior of $\mathrm {Mov}({\mathcal X})$ . Thus, it remains to show that $\Lambda $ is actually movable. Note that X is quasihomogeneous under the action of $\mathrm {Aut}(X)=\mathrm PGL_2(\mathbb {C})$ and there are exactly three orbits $X_0\sqcup X_1\sqcup X_2$ , where $X_0$ is the open orbit and $X_i$ has codimension i for $0\leq i\leq 2$ . Moreover, the closure $\overline {X}_1=X_1\sqcup X_2$ of $X_1$ is a prime divisor in the complete linear system $|2H|$ . In particular, the base locus of $|\Lambda |$ is contained in $\pi ^{-1}(\overline {X}_1)$ . Let $D\in |\Lambda |$ be an arbitrary element. If $\Lambda $ is not movable, then $\pi ^*\overline {X}_1$ is contained in $\operatorname *{\mathrm {Supp}}(D)$ . In particular, $D-\pi ^*\overline {X}_1$ is an effective divisor. This shows that $\Lambda -2\pi ^*H$ is contained in $\mathrm {Eff}({\mathcal X})$ , which contradicts the description of $\mathrm {Eff}({\mathcal X})$ above. Hence, $\Lambda $ is movable, and we have $\mathrm {Mov}({\mathcal X})=\left \langle \Lambda ,\pi ^*H\right \rangle $ .

Recall that there exists a one-dimensional family of lines $l\subseteq X$ on $X,$ such that:

$$\begin{align*}T_X|_l\cong {\mathcal O}_{\mathbb{P}^1}(2)\oplus {\mathcal O}_{\mathbb{P}^1}(1)\oplus {\mathcal O}_{\mathbb{P}^1}(-1). \end{align*}$$

In particular, the nef cone $\mathrm {Nef}({\mathcal X})$ of ${\mathcal X}$ is contained in the cone $\left \langle \Lambda +\pi ^*H,\pi ^*H\right \rangle $ . Thus, it remains to show that $\Lambda +\pi ^*H$ is nef. Note that X is embedded in $\mathbb {P}^6$ by the complete linear system $|H|$ . Therefore, thanks to [15, Lemma 3.1], the vector bundle:

$$\begin{align*}T_X\otimes {\mathcal O}_{\mathbb{P}^6}(3)|_X \otimes {\mathcal O}_X(K_X)\cong T_X\otimes H \end{align*}$$

is globally generated. Hence, the Cartier divisor class $\Lambda +\pi ^*H$ is nef.

Remark 6.2. If X is a Fano manifold of Picard number $1$ , such that the VMRT ${\mathcal C}_x\subset \mathbb {P}(\Omega _{X,x})$ is zero-dimensional, it is proved in [14, Theorem 1.1] that $T_X$ is big if and only if X is isomorphic to the del Pezzo threefold $V_5$ of degree $5$ . In particular, the normalised tangent bundle can not be pseudoeffective by Proposition 6.1.

Now we consider the horospherical $G_2$ -variety $\mathbb {X}$ . We briefly recall the geometric description of $\mathbb {X}$ , and we refer the reader to [43] for more details. First, $\mathbb {X}$ is a seven-dimensional Fano manifold of Picard number $1$ and index $4$ . The automorphism group $\mathrm {Aut}(\mathbb {X})$ acts on $\mathbb {X}$ with two orbits, and the unique closed orbit $Z\subset \mathbb {X}$ is a smooth five-dimension quadric, such that $H|_Z\cong {\mathcal O}_{\mathbb {Q}^5}(1)$ , where H is the ample generator of $\operatorname *{\mathrm {Pic}}(\mathbb {X})$ . In particular, $\Lambda $ is movable. On the other hand, by [44, Proposition 2.3], it follows that there exists a deformation $\mathfrak {X}\rightarrow \Delta $ , such that $\mathfrak {X}_t\cong B_3/P_2$ if $t\not =0$ and $\mathfrak {X}_0\cong \mathbb {X}$ . Then the semicontinuity theorem implies that $T_{\mathbb {X}}$ is big. On the other hand, for $X=B_3/P_2$ , the total dual VMRT $\check {{\mathcal C}}'$ is a prime divisor, such that:

$$\begin{align*}[\check{{\mathcal C}}'] \equiv 4\Lambda' - 2{\pi'}^*H', \end{align*}$$

where $\Lambda '$ is the tautological divisor of $\pi ':\mathbb {P}(T_{B_3/P_2})\rightarrow B_3/P_2$ and $H'$ is the ample generator of $\operatorname *{\mathrm {Pic}}(B_3/P_2)$ (see Proposition 5.9). Moreover, the VMRT of $\mathbb {X}$ at a general point is the smooth surface $\mathbb {P}({\mathcal O}_{\mathbb {P}^1}(1)\oplus {\mathcal O}_{\mathbb {P}^1}(3))$ embedded by ${\mathcal O}(1)$ . This implies that the total dual VMRT $\check {{\mathcal C}}$ of $\mathbb {X}$ is a prime divisor satisfying:

$$\begin{align*}[\check{{\mathcal C}}] \equiv 4\Lambda - 2\pi^*H. \end{align*}$$

In particular, the class $[\Lambda ]$ is not contained in the interior of $\overline {\mathrm {Mov}}(\mathbb {P}(T_{\mathbb {X}}))$ since ${\mathbb B}_{-}(\Lambda )$ contains $\check {{\mathcal C}}$ . This shows that $[\Lambda ]$ generates an extremal ray of $\overline {\mathrm { Mov}}(\mathbb {P}(T_{\mathbb {X} })$ .

Next, denote by ${\mathcal N}$ the normal bundle of Z in $\mathbb {X}$ . Then by adjunction formula, we have $\det ({\mathcal N})\cong {\mathcal O}_{\mathbb {Q}^5}(-1)$ . Denote by $\mathbb {X}'\rightarrow \mathbb {X}$ the blow up along Z with exceptional divisor E. Then it is known that E is isomorphic to the complete flag manifold of $G_2$ -type. In particular, the variety $E\cong \mathbb {P}({\mathcal N}^*)$ is isomorphic to $\mathbb {P}({\mathcal V})$ over $\mathbb {Q}^5$ , where ${\mathcal V}$ is the Cayley bundle over $\mathbb {Q}^5$ (see [42]). As $\det ({\mathcal V})\cong {\mathcal O}_{\mathbb {Q}^5}(-1)$ , there is an isomorphism ${\mathcal N}\cong {\mathcal V}^*(-1)$ .

We claim that we have an isomorphism ${\mathcal V}^*(-1)\cong {\mathcal V}$ . Indeed, it is clear that ${\mathcal V}^*(-1)$ is stable as ${\mathcal V}$ is stable ([42]). Moreover, an easy computation shows that we have:

$$ \begin{align*} c_1({\mathcal V}^*(-1))=c_1({\mathcal V})\quad \text{and} \quad c_2({\mathcal V}^*(-1))=c_2({\mathcal V}). \end{align*} $$

By [42, Main Theorem], the vector bundle ${\mathcal V}^*(-1)$ is isomorphic to ${\mathcal V}$ .

Finally, by [42, Theorem 3.7], the vector bundle ${\mathcal V}(2)$ and, hence, ${\mathcal N}(2)$ are globally generated. As a consequence, it follows from the tangent sequence of Z that the restriction $T_{\mathbb {X}}(2)|_{Z}$ is nef. Moreover, note that $T_{\mathbb {X}}$ is globally generated outside Z, thus, the vector bundle $T_{\mathbb {X}}(2)$ is nef. On the other hand, by [42, Theorem 3.5], there exist lines l on $Z=\mathbb {Q}^5$ , such that:

$$\begin{align*}{\mathcal V}|_l\cong {\mathcal O}_{\mathbb{P}^1}(-2) \oplus {\mathcal O}_{\mathbb{P}^1}(1). \end{align*}$$

This implies that $T_{\mathbb {X}}(a)$ cannot be nef for any $a<2$ and, hence, the divisor $\Lambda + a\pi ^*H$ is nef if and only if $a\geq 2$ . In summary, we have the following result.

Proposition 6.3. Let X be the horospherical $G_2$ -variety $\mathbb {X}$ , and let H be the ample generator of $\operatorname *{\mathrm {Pic}}(X)$ . Denote by $\Lambda $ the tautological divisor class of the projectivised tangent bundle $\pi :{\mathcal X}=\mathbb {P}(T_X)\rightarrow X$ . Then we have:

$$\begin{align*}\begin{cases} \ \,\mathrm{Eff}({\mathcal X})=\left\langle 4\Lambda-2\pi^*H,\pi^*H \right\rangle \\ \mathrm{Mov}({\mathcal X}) =\left\langle \Lambda,\pi^*H\right\rangle \\ \ \mathrm{Nef}({\mathcal X})=\left\langle \Lambda+2\pi^*H,\pi^*H\right\rangle. \end{cases} \end{align*}$$

Remark 6.4. Recently the second author has found in [31] infinitely many nonhomogeneous Fano manifolds of Picard number $1$ and with big tangent bundle.