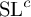Introduction
Around 40 years ago, Arason computed the Witt groups of projective spaces [Reference ArasonAra80]. This computation was later revisited by Gille [Reference GilleGil01], Walter [Reference WalterWal03] and Nenashev [Reference NenashevNen09]. It exhibited Witt groups as a somewhat exotic cohomology theory, whose value on projective spaces differs quite drastically from what is obtained in more classical cohomology theories such as Chow groups or K-theory. It is now understood that this behaviour reflects the lack of
![]() $\operatorname {\mathrm {GL}}$
-orientation in Witt theory.
$\operatorname {\mathrm {GL}}$
-orientation in Witt theory.
Ananyevskiy observed in [Reference AnanyevskiyAna16a] that the key property of Witt groups permitting to perform these computations turns out to be the fact that the Hopf map
induces by pullback an isomorphism of Witt groups
![]() $\operatorname {\mathrm {W}}(\mathbb {P}^1) \xrightarrow {\sim } \operatorname {\mathrm {W}}({\mathbb {A}}^2 \smallsetminus \{0\})$
. He thus extended in [Reference AnanyevskiyAna16a] the above-mentioned computations to arbitrary cohomology theories in which
$\operatorname {\mathrm {W}}(\mathbb {P}^1) \xrightarrow {\sim } \operatorname {\mathrm {W}}({\mathbb {A}}^2 \smallsetminus \{0\})$
. He thus extended in [Reference AnanyevskiyAna16a] the above-mentioned computations to arbitrary cohomology theories in which
![]() $\eta $
induces an isomorphism.
$\eta $
induces an isomorphism.
Inverting the Hopf map
![]() $\eta $
in the motivic stable homotopy category
$\eta $
in the motivic stable homotopy category
![]() $\operatorname {\mathrm {SH}}(S)$
over a base scheme S yields its
$\operatorname {\mathrm {SH}}(S)$
over a base scheme S yields its
![]() $\eta $
-periodic version
$\eta $
-periodic version
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, a category which has been studied in details by Bachmann–Hopkins [Reference Bachmann and HopkinsBH20]. In this paper, we lift Ananyevskiy’s computations of the cohomology of projective spaces to the
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, a category which has been studied in details by Bachmann–Hopkins [Reference Bachmann and HopkinsBH20]. In this paper, we lift Ananyevskiy’s computations of the cohomology of projective spaces to the
![]() $\eta $
-periodic stable homotopy category: We obtain for instance that a projective bundle of even relative dimension becomes an isomorphism in
$\eta $
-periodic stable homotopy category: We obtain for instance that a projective bundle of even relative dimension becomes an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
Another familiar feature of Witt groups is that twisting these groups by squares of line bundles has no effect, which may be viewed as a manifestation of the
![]() $\operatorname {\mathrm {SL}}^c$
-orientability of Witt groups (see below). We show that that property of Witt groups in fact follows from their
$\operatorname {\mathrm {SL}}^c$
-orientability of Witt groups (see below). We show that that property of Witt groups in fact follows from their
![]() $\eta $
-periodicity alone (see (4.3.2) for a more general statement).
$\eta $
-periodicity alone (see (4.3.2) for a more general statement).
Proposition. Let
![]() $V \to X$
be a vector bundle and
$V \to X$
be a vector bundle and
![]() $L \to X$
a line bundle. Then we have an isomorphism of Thom spaces
$L \to X$
a line bundle. Then we have an isomorphism of Thom spaces
Panin and Walter introduced [Reference Panin and WalterPW18, §3] the notion of
![]() $\operatorname {\mathrm {SL}}^c$
-orientability for algebraic cohomology theories, which consists of the data of Thom classes for vector bundles equipped with a square root of their determinant and proved that Hermitian K-theory is
$\operatorname {\mathrm {SL}}^c$
-orientability for algebraic cohomology theories, which consists of the data of Thom classes for vector bundles equipped with a square root of their determinant and proved that Hermitian K-theory is
![]() $\operatorname {\mathrm {SL}}^c$
-oriented. Ananyevskiy later showed [Reference AnanyevskiyAna20, Theorem 1.2] that a cohomology theory is
$\operatorname {\mathrm {SL}}^c$
-oriented. Ananyevskiy later showed [Reference AnanyevskiyAna20, Theorem 1.2] that a cohomology theory is
![]() $\operatorname {\mathrm {SL}}^c$
-oriented as soon as it is a Zariski sheaf in bidegree
$\operatorname {\mathrm {SL}}^c$
-oriented as soon as it is a Zariski sheaf in bidegree
![]() $(0,0)$
and pointed out [Reference AnanyevskiyAna20, Theorem 1.1] the close relations between
$(0,0)$
and pointed out [Reference AnanyevskiyAna20, Theorem 1.1] the close relations between
![]() $\operatorname {\mathrm {SL}}^c$
-orientations and
$\operatorname {\mathrm {SL}}^c$
-orientations and
![]() $\operatorname {\mathrm {SL}}$
-orientations (the latter consisting in the data of Thom classes for vector bundles with trivialised determinant). We show in this paper that the two notions actually coincide in the
$\operatorname {\mathrm {SL}}$
-orientations (the latter consisting in the data of Thom classes for vector bundles with trivialised determinant). We show in this paper that the two notions actually coincide in the
![]() $\eta $
-periodic context.
$\eta $
-periodic context.
Theorem. Every
![]() $\operatorname {\mathrm {SL}}$
-orientation of an
$\operatorname {\mathrm {SL}}$
-orientation of an
![]() $\eta $
-periodic motivic commutative ring spectrum is induced by a unique
$\eta $
-periodic motivic commutative ring spectrum is induced by a unique
![]() $\operatorname {\mathrm {SL}}^c$
-orientation.
$\operatorname {\mathrm {SL}}^c$
-orientation.
These results are obtained as consequences of the following observation.
Proposition. Let E be a vector bundle of odd rank over a smooth S-scheme X and
![]() $E^\circ $
the complement of the zero-section in E.
$E^\circ $
the complement of the zero-section in E.
-
(i) The projection
 $E^\circ \to X$
admits a section in
$E^\circ \to X$
admits a section in
 $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
. -
(ii) The diagram
 $E^\circ \times _X E^\circ \rightrightarrows E^\circ \to X$
becomes a split coequaliser diagram in
$E^\circ \times _X E^\circ \rightrightarrows E^\circ \to X$
becomes a split coequaliser diagram in
 $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
The first assertion may be viewed as a splitting principle, while the second permits performing a form of descent. To some extent, this proposition allows us to assume that odd rank vector bundles admit a nowhere-vanishing section (once
![]() $\eta $
is inverted); in particular that line bundles are trivial.
$\eta $
is inverted); in particular that line bundles are trivial.
Finally, we provide applications to the computation in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
of the étale classifying spaces of certain algebraic groups.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
of the étale classifying spaces of certain algebraic groups.
Theorem. For
![]() $r \in \mathbb {N} \smallsetminus \{0\}$
, there exist natural maps
$r \in \mathbb {N} \smallsetminus \{0\}$
, there exist natural maps
which become isomorphisms in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
From this theorem, we deduce a computation in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
of the classifying space of an arbitrary diagonalisable group. We obtain that all invariants of torsors under a diagonalisable group with values in an
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
of the classifying space of an arbitrary diagonalisable group. We obtain that all invariants of torsors under a diagonalisable group with values in an
![]() $\eta $
-periodic cohomology theory arise from a single invariant of
$\eta $
-periodic cohomology theory arise from a single invariant of
![]() $\mu _2$
-torsors. In the appendix, we present an explicit construction of that invariant, exploiting the identification of the group
$\mu _2$
-torsors. In the appendix, we present an explicit construction of that invariant, exploiting the identification of the group
![]() $\mu _2$
with the orthogonal group
$\mu _2$
with the orthogonal group
![]() $\operatorname {\mathrm {O}}_1$
.
$\operatorname {\mathrm {O}}_1$
.
Next, we obtain ‘relative’ computations in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
of certain étale classifying spaces in terms of others.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
of certain étale classifying spaces in terms of others.
Theorem. For
![]() $n\in \mathbb {N}\smallsetminus \{0\}$
and
$n\in \mathbb {N}\smallsetminus \{0\}$
and
![]() $r\in \mathbb {N}$
, the natural morphisms
$r\in \mathbb {N}$
, the natural morphisms
become isomorphisms in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
The first result can be viewed as a companion of the theorem on orientations stated above and cements the idea that the groups
![]() $\operatorname {\mathrm {SL}}_n^c$
and
$\operatorname {\mathrm {SL}}_n^c$
and
![]() $\operatorname {\mathrm {SL}}_n$
are the same in the eyes of
$\operatorname {\mathrm {SL}}_n$
are the same in the eyes of
![]() $\eta $
-periodic stable homotopy theory. The second (resp. third) result expresses the fact that odd-dimensional vector bundles behave as if they had a nowhere-vanishing section (resp. trivial determinant) from the point of view of
$\eta $
-periodic stable homotopy theory. The second (resp. third) result expresses the fact that odd-dimensional vector bundles behave as if they had a nowhere-vanishing section (resp. trivial determinant) from the point of view of
![]() $\eta $
-periodic stable homotopy theory.
$\eta $
-periodic stable homotopy theory.
The morphism
![]() $\operatorname {\mathrm {BSL}}_{2r} \to \operatorname {\mathrm {BGL}}_{2r}$
is not an isomorphism in
$\operatorname {\mathrm {BSL}}_{2r} \to \operatorname {\mathrm {BGL}}_{2r}$
is not an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, but we show that it admits a section, expressing the fact that every invariant (with values in an
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, but we show that it admits a section, expressing the fact that every invariant (with values in an
![]() $\eta $
-periodic cohomology theory) of even-dimensional vector bundles is determined by its value on those bundles having trivial determinant.
$\eta $
-periodic cohomology theory) of even-dimensional vector bundles is determined by its value on those bundles having trivial determinant.
Finally, let us mention that the results of this paper serve as a starting point for the paper [Reference HautionHau22] on Pontryagin classes.
1 Notation and basic facts
1.1
Throughout the paper, we work over a noetherian base scheme S of finite dimension. The category of smooth separated S-schemes of finite type will be denoted by
![]() $\operatorname {\mathrm {Sm}}_S$
. All schemes will be implicitly assumed to belong to
$\operatorname {\mathrm {Sm}}_S$
. All schemes will be implicitly assumed to belong to
![]() $\operatorname {\mathrm {Sm}}_S$
, and the notation
$\operatorname {\mathrm {Sm}}_S$
, and the notation
![]() ${\mathbb {A}}^n,\mathbb {P}^n,\mathbb {G}_m$
will refer to the corresponding S-schemes. We will denote by
${\mathbb {A}}^n,\mathbb {P}^n,\mathbb {G}_m$
will refer to the corresponding S-schemes. We will denote by
![]() $1$
the trivial line bundle over a given scheme in
$1$
the trivial line bundle over a given scheme in
![]() $\operatorname {\mathrm {Sm}}_S$
.
$\operatorname {\mathrm {Sm}}_S$
.
1.2
We will use the
![]() ${\mathbb {A}}^1$
-homotopy theory introduced by Morel–Voevodsky [Reference Morel and VoevodskyMV99]. We will denote by
${\mathbb {A}}^1$
-homotopy theory introduced by Morel–Voevodsky [Reference Morel and VoevodskyMV99]. We will denote by
![]() $\operatorname {\mathrm {Spc}}(S)$
the category of motivic spaces (i.e., simplicial presheaves on
$\operatorname {\mathrm {Spc}}(S)$
the category of motivic spaces (i.e., simplicial presheaves on
![]() $\operatorname {\mathrm {Sm}}_S$
), by
$\operatorname {\mathrm {Sm}}_S$
), by
![]() ${\mathrm{Spc}_{\bullet }}(S)$
its pointed version and by
${\mathrm{Spc}_{\bullet }}(S)$
its pointed version and by
![]() $\operatorname {\mathrm {Spt}}(S)$
the category of T-spectra, where
$\operatorname {\mathrm {Spt}}(S)$
the category of T-spectra, where
![]() ${T= {\mathbb {A}}^1/\mathbb {G}_m}$
. We endow these with the motivic equivalences, resp. stable motivic equivalences, and denote by
${T= {\mathbb {A}}^1/\mathbb {G}_m}$
. We endow these with the motivic equivalences, resp. stable motivic equivalences, and denote by
![]() $\operatorname {\mathrm {H}}(S), \mathrm {H}_{\bullet }(S), \operatorname {\mathrm {SH}}(S)$
the respective homotopy categories. We refer to, for example, [Reference Panin, Pimenov and RöndigsPPR09, Appendix A] for more details.
$\operatorname {\mathrm {H}}(S), \mathrm {H}_{\bullet }(S), \operatorname {\mathrm {SH}}(S)$
the respective homotopy categories. We refer to, for example, [Reference Panin, Pimenov and RöndigsPPR09, Appendix A] for more details.
We have an infinite suspension functor
![]() $\Sigma ^{\infty }\colon {\mathrm{Spc}_{\bullet }}(S) \to \operatorname {\mathrm {Spt}}(S)$
. Composing with the functor
$\Sigma ^{\infty }\colon {\mathrm{Spc}_{\bullet }}(S) \to \operatorname {\mathrm {Spt}}(S)$
. Composing with the functor
![]() $\operatorname {\mathrm {Spc}}(S) \to {\mathrm{Spc}_{\bullet }}(S)$
adding an external base point, we obtain a functor
$\operatorname {\mathrm {Spc}}(S) \to {\mathrm{Spc}_{\bullet }}(S)$
adding an external base point, we obtain a functor
![]() $\Sigma ^{\infty }_+ \colon \operatorname {\mathrm {Spc}}(S) \to \operatorname {\mathrm {Spt}}(S)$
.
$\Sigma ^{\infty }_+ \colon \operatorname {\mathrm {Spc}}(S) \to \operatorname {\mathrm {Spt}}(S)$
.
The spheres are denoted as usual by
![]() $S^{p,q} \in {\mathrm{Spc}_{\bullet }}(S)$
for
$S^{p,q} \in {\mathrm{Spc}_{\bullet }}(S)$
for
![]() $p,q\in \mathbb {N}$
with
$p,q\in \mathbb {N}$
with
![]() $p\geq q$
(where
$p\geq q$
(where
![]() $T\simeq S^{2,1}$
). The motivic sphere spectrum
$T\simeq S^{2,1}$
). The motivic sphere spectrum
![]() $\Sigma ^{\infty }_+ S$
will be denoted by
$\Sigma ^{\infty }_+ S$
will be denoted by
![]() $\mathbf {1}_S \in \operatorname {\mathrm {Spt}}(S)$
. When A is a motivic spectrum, we denote its
$\mathbf {1}_S \in \operatorname {\mathrm {Spt}}(S)$
. When A is a motivic spectrum, we denote its
![]() $(p,q)$
-th suspension by
$(p,q)$
-th suspension by
![]() $\Sigma ^{p,q}A = S^{p,q} \wedge A$
. This yields functors
$\Sigma ^{p,q}A = S^{p,q} \wedge A$
. This yields functors
![]() $\Sigma ^{p,q} \colon \operatorname {\mathrm {SH}}(S) \to \operatorname {\mathrm {SH}}(S)$
for
$\Sigma ^{p,q} \colon \operatorname {\mathrm {SH}}(S) \to \operatorname {\mathrm {SH}}(S)$
for
![]() $p,q\in \mathbb {Z}$
.
$p,q\in \mathbb {Z}$
.
1.3
When
![]() $E\to X$
is a vector bundle with
$E\to X$
is a vector bundle with
![]() $X \in \operatorname {\mathrm {Sm}}_S$
, we denote by
$X \in \operatorname {\mathrm {Sm}}_S$
, we denote by
![]() $E^{\circ }=E \smallsetminus X$
the complement of the zero section. The Thom space of E is the pointed motivic space
$E^{\circ }=E \smallsetminus X$
the complement of the zero section. The Thom space of E is the pointed motivic space
![]() $\operatorname {\mathrm {Th}}_X(E) = E/E^\circ $
. We will write
$\operatorname {\mathrm {Th}}_X(E) = E/E^\circ $
. We will write
![]() $\operatorname {\mathrm {Th}}_X(E) \in \operatorname {\mathrm {Spt}}(S)$
instead of
$\operatorname {\mathrm {Th}}_X(E) \in \operatorname {\mathrm {Spt}}(S)$
instead of
![]() $\Sigma ^{\infty } \operatorname {\mathrm {Th}}_X(E)$
, in order to lighten the notation. When
$\Sigma ^{\infty } \operatorname {\mathrm {Th}}_X(E)$
, in order to lighten the notation. When
![]() $g \colon Y \to X$
is a morphism in
$g \colon Y \to X$
is a morphism in
![]() $\operatorname {\mathrm {Sm}}_S$
, we will usually write
$\operatorname {\mathrm {Sm}}_S$
, we will usually write
![]() $\operatorname {\mathrm {Th}}_Y(E)$
instead of
$\operatorname {\mathrm {Th}}_Y(E)$
instead of
![]() $\operatorname {\mathrm {Th}}_Y(g^*E)$
. Since
$\operatorname {\mathrm {Th}}_Y(g^*E)$
. Since
![]() $E \to X$
is a weak equivalence, we have a cofiber sequence in
$E \to X$
is a weak equivalence, we have a cofiber sequence in
![]() ${\mathrm{Spc}_{\bullet }}(S)$
, where
${\mathrm{Spc}_{\bullet }}(S)$
, where
![]() $p \colon E^\circ \to X$
is the projection,
$p \colon E^\circ \to X$
is the projection,
If
![]() $F \to S$
is a vector bundle and
$F \to S$
is a vector bundle and
![]() $f \colon X \to S$
the structural morphism, we have by [Reference Morel and VoevodskyMV99, Proposition 3.2.17 (1)] a natural identification in
$f \colon X \to S$
the structural morphism, we have by [Reference Morel and VoevodskyMV99, Proposition 3.2.17 (1)] a natural identification in
![]() ${\mathrm{Spc}_{\bullet }}(S)$
${\mathrm{Spc}_{\bullet }}(S)$
When
![]() $V \to S$
is a vector bundle, we denote by
$V \to S$
is a vector bundle, we denote by
![]() $\Sigma ^V \colon \operatorname {\mathrm {SH}}(S) \to \operatorname {\mathrm {SH}}(S)$
the derived functor induced by
$\Sigma ^V \colon \operatorname {\mathrm {SH}}(S) \to \operatorname {\mathrm {SH}}(S)$
the derived functor induced by
![]() $A \mapsto A \wedge \operatorname {\mathrm {Th}}_S(V)$
. It is an equivalence of categories, with inverse denoted by
$A \mapsto A \wedge \operatorname {\mathrm {Th}}_S(V)$
. It is an equivalence of categories, with inverse denoted by
![]() $\Sigma ^{-V}$
.
$\Sigma ^{-V}$
.
1.4
Let
![]() $i \colon Y\to X$
be a closed immersion in
$i \colon Y\to X$
be a closed immersion in
![]() $\operatorname {\mathrm {Sm}}_S$
, with normal bundle
$\operatorname {\mathrm {Sm}}_S$
, with normal bundle
![]() $N \to Y$
, and open complement
$N \to Y$
, and open complement
![]() $u\colon U \to X$
. The purity equivalence
$u\colon U \to X$
. The purity equivalence
![]() $X/U \simeq \operatorname {\mathrm {Th}}_Y(N)$
(see, e.g., [Reference Morel and VoevodskyMV99, Theorem 3.2.23]) yields a cofiber sequence in
$X/U \simeq \operatorname {\mathrm {Th}}_Y(N)$
(see, e.g., [Reference Morel and VoevodskyMV99, Theorem 3.2.23]) yields a cofiber sequence in
![]() ${\mathrm{Spc}_{\bullet }}(S)$
${\mathrm{Spc}_{\bullet }}(S)$
More generally, if
![]() $V \to X$
is a vector bundle, we have a cofiber sequence in
$V \to X$
is a vector bundle, we have a cofiber sequence in
![]() ${\mathrm{Spc}_{\bullet }}(S)$
${\mathrm{Spc}_{\bullet }}(S)$
This may be deduced from equation (1.4.a) by first reducing to the case
![]() $X=S$
using the functor
$X=S$
using the functor
![]() $f_\sharp $
of (1.9) below and then applying the functor
$f_\sharp $
of (1.9) below and then applying the functor
![]() $- \wedge \operatorname {\mathrm {Th}}_X(V)$
(both of which preserve homotopy colimits), in view of equation (1.3.b).
$- \wedge \operatorname {\mathrm {Th}}_X(V)$
(both of which preserve homotopy colimits), in view of equation (1.3.b).
1.5
Let
![]() $\varphi \colon E \xrightarrow {\sim } F$
be an isomorphism of vector bundles over
$\varphi \colon E \xrightarrow {\sim } F$
be an isomorphism of vector bundles over
![]() $X \in \operatorname {\mathrm {Sm}}_S$
. Then
$X \in \operatorname {\mathrm {Sm}}_S$
. Then
![]() $\varphi $
induces a weak equivalence in
$\varphi $
induces a weak equivalence in
![]() ${\mathrm{Spc}_{\bullet }}(S)$
(and
${\mathrm{Spc}_{\bullet }}(S)$
(and
![]() $\operatorname {\mathrm {Spt}}(S)$
)
$\operatorname {\mathrm {Spt}}(S)$
)
If
![]() $\psi \colon F \xrightarrow {\sim } G$
is an isomorphism of vector bundles over X, we have
$\psi \colon F \xrightarrow {\sim } G$
is an isomorphism of vector bundles over X, we have
If
![]() $X=S$
and
$X=S$
and
![]() $f\in \operatorname {\mathrm {End}}_{\operatorname {\mathrm {SH}}(S)}(\mathbf {1}_S)$
, then we have in
$f\in \operatorname {\mathrm {End}}_{\operatorname {\mathrm {SH}}(S)}(\mathbf {1}_S)$
, then we have in
![]() $\operatorname {\mathrm {SH}}(S)$
$\operatorname {\mathrm {SH}}(S)$
(This follows from the fact that, as morphisms
![]() $\mathbf {1}_S \wedge \operatorname {\mathrm {Th}}_S(E) \to \mathbf {1}_S \wedge \operatorname {\mathrm {Th}}_S(F)$
$\mathbf {1}_S \wedge \operatorname {\mathrm {Th}}_S(E) \to \mathbf {1}_S \wedge \operatorname {\mathrm {Th}}_S(F)$
1.6
(See [Reference MorelMor04, Lemma 6.3.4].) Let
![]() $X \in \operatorname {\mathrm {Sm}}_S$
and
$X \in \operatorname {\mathrm {Sm}}_S$
and
![]() $u\in H^0(X,\mathbb {G}_m)$
. Consider the automorphism
$u\in H^0(X,\mathbb {G}_m)$
. Consider the automorphism
![]() $u \operatorname {\mathrm {id}}_1 \colon 1 \to 1$
of the trivial line bundle over X, and set
$u \operatorname {\mathrm {id}}_1 \colon 1 \to 1$
of the trivial line bundle over X, and set
It follows from equation (1.5.a) that
When
![]() $X=S$
and
$X=S$
and
![]() $A \in \operatorname {\mathrm {SH}}(S)$
, we will denote again by
$A \in \operatorname {\mathrm {SH}}(S)$
, we will denote again by
![]() $\langle u \rangle \in \operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {SH}}(S)}(A)$
the morphism
$\langle u \rangle \in \operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {SH}}(S)}(A)$
the morphism
If
![]() $f\colon A \to B$
is a morphism in
$f\colon A \to B$
is a morphism in
![]() $\operatorname {\mathrm {SH}}(S)$
, then
$\operatorname {\mathrm {SH}}(S)$
, then
1.7
We denote by
![]() $\eta \colon {\mathbb {A}}^2 \smallsetminus \{0\} \to \mathbb {P}^1$
in
$\eta \colon {\mathbb {A}}^2 \smallsetminus \{0\} \to \mathbb {P}^1$
in
![]() ${\mathrm{Spc}_{\bullet }}(S)$
the map
${\mathrm{Spc}_{\bullet }}(S)$
the map
![]() $(x,y) \mapsto [x:y]$
, where
$(x,y) \mapsto [x:y]$
, where
![]() ${\mathbb {A}}^2\smallsetminus \{0\}$
is pointed by
${\mathbb {A}}^2\smallsetminus \{0\}$
is pointed by
![]() $(1,1)$
and
$(1,1)$
and
![]() $\mathbb {P}^1$
by
$\mathbb {P}^1$
by
![]() $[1:1]$
.
$[1:1]$
.
1.8
We will consider the categories
![]() ${\mathrm{Spc}_{\bullet }}(S)[\eta ^{-1}]$
and
${\mathrm{Spc}_{\bullet }}(S)[\eta ^{-1}]$
and
![]() $\operatorname {\mathrm {Spt}}(S)[\eta ^{-1}]$
obtained by monoidally inverting the map
$\operatorname {\mathrm {Spt}}(S)[\eta ^{-1}]$
obtained by monoidally inverting the map
![]() $\eta $
of equation (1.7), which can be constructed as left Bousfield localisations, as discussed in [Reference BachmannBac18, §6]. Their respective homotopy categories will be denoted by
$\eta $
of equation (1.7), which can be constructed as left Bousfield localisations, as discussed in [Reference BachmannBac18, §6]. Their respective homotopy categories will be denoted by
![]() $H_{\bullet }(S)[\eta ^{-1}]$
and
$H_{\bullet }(S)[\eta ^{-1}]$
and
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, and we will usually omit the mention of the localisation functors.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, and we will usually omit the mention of the localisation functors.
A spectrum
![]() $A \in \operatorname {\mathrm {Spt}}(S)$
is called
$A \in \operatorname {\mathrm {Spt}}(S)$
is called
![]() $\eta $
-periodic if the map
$\eta $
-periodic if the map
is an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)$
. The full subcategory of such objects in
$\operatorname {\mathrm {SH}}(S)$
. The full subcategory of such objects in
![]() $\operatorname {\mathrm {Spt}}(S)$
can be identified
$\operatorname {\mathrm {Spt}}(S)$
can be identified
![]() $\operatorname {\mathrm {Spt}}(S)[\eta ^{-1}]$
.
$\operatorname {\mathrm {Spt}}(S)[\eta ^{-1}]$
.
1.9
Let
![]() $X \in \operatorname {\mathrm {Sm}}_S$
with structural morphism
$X \in \operatorname {\mathrm {Sm}}_S$
with structural morphism
![]() $f\colon X \to S$
. Then there are Quillen adjunctions
$f\colon X \to S$
. Then there are Quillen adjunctions
The functor
![]() $f^*$
is induced by base-change, while
$f^*$
is induced by base-change, while
![]() $f_\sharp $
arises from viewing a smooth X-scheme as a smooth S-scheme by composing with f. These induce Quillen adjunctions
$f_\sharp $
arises from viewing a smooth X-scheme as a smooth S-scheme by composing with f. These induce Quillen adjunctions
We will also use the notation
![]() $f^*,f_{\sharp }$
for the derived functors on the respective homotopy categories.
$f^*,f_{\sharp }$
for the derived functors on the respective homotopy categories.
1.10
(See, e.g., [Reference Dugger, Hollander and IsaksenDHI04].) Let
![]() $V \to X$
be a vector bundle with
$V \to X$
be a vector bundle with
![]() $X \in \operatorname {\mathrm {Sm}}_S$
and
$X \in \operatorname {\mathrm {Sm}}_S$
and
![]() $U_\alpha $
an open covering of X. Then the map
$U_\alpha $
an open covering of X. Then the map
 $$\begin{align*}\operatorname{\mathrm{hocolim}} \Big( \cdots\mathrel{\substack{\scriptstyle\rightarrow\\[-0.55ex] \scriptstyle\rightarrow \\[-0.55ex] \scriptstyle\rightarrow}} \coprod_{\alpha,\beta} \operatorname{\mathrm{Th}}_{U_\alpha \cap U_\beta}(V|_{U_\alpha \cap U_\beta}) \rightrightarrows \coprod_\alpha \operatorname{\mathrm{Th}}_{U_\alpha}(V|_{U_\alpha})\Big) \to \operatorname{\mathrm{Th}}_X(V) \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{hocolim}} \Big( \cdots\mathrel{\substack{\scriptstyle\rightarrow\\[-0.55ex] \scriptstyle\rightarrow \\[-0.55ex] \scriptstyle\rightarrow}} \coprod_{\alpha,\beta} \operatorname{\mathrm{Th}}_{U_\alpha \cap U_\beta}(V|_{U_\alpha \cap U_\beta}) \rightrightarrows \coprod_\alpha \operatorname{\mathrm{Th}}_{U_\alpha}(V|_{U_\alpha})\Big) \to \operatorname{\mathrm{Th}}_X(V) \end{align*}$$
is a weak equivalence.
2 Splitting
 $\mathbb {G}_m$
-torsors
$\mathbb {G}_m$
-torsors
2.1 Local splitting
In this section, we consider the schemes
![]() ${\mathbb {A}}^1,\mathbb {G}_m,\mathbb {P}^1,{\mathbb {A}}^2\smallsetminus \{0\}$
as pointed motivic spaces, respectively via
${\mathbb {A}}^1,\mathbb {G}_m,\mathbb {P}^1,{\mathbb {A}}^2\smallsetminus \{0\}$
as pointed motivic spaces, respectively via
![]() $1,1,[1:1],(1,1)$
. We recall that
$1,1,[1:1],(1,1)$
. We recall that
![]() $T={\mathbb {A}}^1/\mathbb {G}_m$
. We have a chain of weak equivalences
$T={\mathbb {A}}^1/\mathbb {G}_m$
. We have a chain of weak equivalences
where the first arrow is induced by the immersion
![]() ${\mathbb {A}}^1 \to \mathbb {P}^1, x \mapsto [x:1]$
, and the quotient
${\mathbb {A}}^1 \to \mathbb {P}^1, x \mapsto [x:1]$
, and the quotient
![]() $\mathbb {P}^1/{\mathbb {A}}^1$
is taken with respect to the immersion
$\mathbb {P}^1/{\mathbb {A}}^1$
is taken with respect to the immersion
![]() ${\mathbb {A}}^1 \to \mathbb {P}^1, y \mapsto [1:y]$
.
${\mathbb {A}}^1 \to \mathbb {P}^1, y \mapsto [1:y]$
.
We first recall a well-known fact (see, e.g., [Reference AnanyevskiyAna20, Lemma 6.2] for a stable version):
2.1.1 Lemma. Let
![]() $u \in H^0(S,\mathbb {G}_m)$
. Then the morphism
$u \in H^0(S,\mathbb {G}_m)$
. Then the morphism
![]() $\operatorname {\mathrm {Th}}(u^2 \operatorname {\mathrm {id}}_1) \colon T \to T$
(see (1.5)) coincides with the identity in
$\operatorname {\mathrm {Th}}(u^2 \operatorname {\mathrm {id}}_1) \colon T \to T$
(see (1.5)) coincides with the identity in
![]() $\mathrm{H}_{\bullet }(S)$
.
$\mathrm{H}_{\bullet }(S)$
.
Proof. The endomorphism
![]() $\varphi \colon \mathbb {P}^1 \to \mathbb {P}^1$
given by
$\varphi \colon \mathbb {P}^1 \to \mathbb {P}^1$
given by
![]() $[x:y] \mapsto [u^2x:y]=[ux:u^{-1}y]$
is induced by the matrix
$[x:y] \mapsto [u^2x:y]=[ux:u^{-1}y]$
is induced by the matrix
 $$\begin{align*}A= \begin{pmatrix} u & 0\\ 0 & u^{-1}\\ \end{pmatrix}. \end{align*}$$
$$\begin{align*}A= \begin{pmatrix} u & 0\\ 0 & u^{-1}\\ \end{pmatrix}. \end{align*}$$
Since
 $$\begin{align*}A = \begin{pmatrix} 1 & u\\ 0 & 1\\ \end{pmatrix} \begin{pmatrix} 1 & 0\\ -u^{-1} & 1\\ \end{pmatrix} \begin{pmatrix} 1 & u-1\\ 0 & 1\\ \end{pmatrix} \begin{pmatrix} 1 & 0\\ 1 & 1\\ \end{pmatrix} \begin{pmatrix} 1 & -1\\ 0 & 1\\ \end{pmatrix} \end{align*}$$
$$\begin{align*}A = \begin{pmatrix} 1 & u\\ 0 & 1\\ \end{pmatrix} \begin{pmatrix} 1 & 0\\ -u^{-1} & 1\\ \end{pmatrix} \begin{pmatrix} 1 & u-1\\ 0 & 1\\ \end{pmatrix} \begin{pmatrix} 1 & 0\\ 1 & 1\\ \end{pmatrix} \begin{pmatrix} 1 & -1\\ 0 & 1\\ \end{pmatrix} \end{align*}$$
is a product of transvections, the endomorphism
![]() $\varphi $
induces the identity endomorphism of
$\varphi $
induces the identity endomorphism of
![]() $\mathbb {P}^1_+$
in
$\mathbb {P}^1_+$
in
![]() $\mathrm{H}_{\bullet }(S)$
(see, e.g., [Reference AnanyevskiyAna16a, Lemma 1]). The map
$\mathrm{H}_{\bullet }(S)$
(see, e.g., [Reference AnanyevskiyAna16a, Lemma 1]). The map
![]() $\varphi $
stabilises the copies of
$\varphi $
stabilises the copies of
![]() ${\mathbb {A}}^1$
given by
${\mathbb {A}}^1$
given by
![]() $x \mapsto [x:1]$
and
$x \mapsto [x:1]$
and
![]() $y \mapsto [1:y]$
and restricts to
$y \mapsto [1:y]$
and restricts to
![]() $u^2 \operatorname {\mathrm {id}}_1$
on the former. Thus, the statement follows from the isomorphism (2.1.0.a).
$u^2 \operatorname {\mathrm {id}}_1$
on the former. Thus, the statement follows from the isomorphism (2.1.0.a).
2.1.2
Excision yields isomorphisms in
![]() $\mathrm{H}_{\bullet }(S)$
$\mathrm{H}_{\bullet }(S)$
Composing with the quotient
![]() ${\mathbb {A}}^2 \smallsetminus \{0\} \to ({\mathbb {A}}^2 \smallsetminus \{0\})/({\mathbb {A}}^1 \times \mathbb {G}_m)$
, this yields a map
${\mathbb {A}}^2 \smallsetminus \{0\} \to ({\mathbb {A}}^2 \smallsetminus \{0\})/({\mathbb {A}}^1 \times \mathbb {G}_m)$
, this yields a map
Lemma 2.1.3. The projection
![]() $p\colon \mathbb {G}_m \to S$
induces a cofiber sequence in
$p\colon \mathbb {G}_m \to S$
induces a cofiber sequence in
![]() ${\mathrm{Spc}_{\bullet }}(S)$
${\mathrm{Spc}_{\bullet }}(S)$
Proof. This follows from the consideration of the following commutative diagram in
![]() ${\mathrm{Spc}_{\bullet }}(S)$
, whose rows are cofiber sequences
${\mathrm{Spc}_{\bullet }}(S)$
, whose rows are cofiber sequences

and where the curved arrow is the weak equivalence induced by the projection
![]() ${\mathbb {G}_m \times {\mathbb {A}}^1 \to \mathbb {G}_m}$
.
${\mathbb {G}_m \times {\mathbb {A}}^1 \to \mathbb {G}_m}$
.
The next lemma is reminiscent of [Reference AnanyevskiyAna16b, Theorem 3.8]:
Lemma 2.1.4. The morphism
![]() $\eta $
of (1.7) factors in
$\eta $
of (1.7) factors in
![]() $\mathrm{H}_{\bullet }(S)$
as
$\mathrm{H}_{\bullet }(S)$
as
where
![]() $t \in H^0(\mathbb {G}_m,\mathbb {G}_m)$
is the tautological section and
$t \in H^0(\mathbb {G}_m,\mathbb {G}_m)$
is the tautological section and
![]() $p\colon \mathbb {G}_m \to S$
the projection (and
$p\colon \mathbb {G}_m \to S$
the projection (and
![]() $T \wedge (\mathbb {G}_m)_+$
is identified with
$T \wedge (\mathbb {G}_m)_+$
is identified with
![]() $\operatorname {\mathrm {Th}}_{\mathbb {G}_m}(1)$
).
$\operatorname {\mathrm {Th}}_{\mathbb {G}_m}(1)$
).
Proof. Consider the commutative diagram in
![]() $\operatorname {\mathrm {Sm}}_S$
$\operatorname {\mathrm {Sm}}_S$

where the upper horizontal arrow is the natural open immersion, the lower horizontal arrow is given by
![]() $x \mapsto [x:1]$
and
$x \mapsto [x:1]$
and
![]() $\mu $
is given by
$\mu $
is given by
![]() $(x,y) \mapsto xy^{-1}$
. Excision yields the isomorphisms in the commutative diagram in
$(x,y) \mapsto xy^{-1}$
. Excision yields the isomorphisms in the commutative diagram in
![]() $\mathrm{H}_{\bullet }(S)$
$\mathrm{H}_{\bullet }(S)$

where
![]() $\tilde {\mu }$
is induced by
$\tilde {\mu }$
is induced by
![]() $\mu $
, and the lower horizontal arrows are the morphisms of equation (2.1.0.a). To conclude, observe that the morphism
$\mu $
, and the lower horizontal arrows are the morphisms of equation (2.1.0.a). To conclude, observe that the morphism
![]() $\tilde {\mu }$
factors as the upper horizontal composite in the following commutative diagram in
$\tilde {\mu }$
factors as the upper horizontal composite in the following commutative diagram in
![]() $H_{\bullet }(S)$
:
$H_{\bullet }(S)$
:

Proposition 2.1.5. Let
![]() $p \colon \mathbb {G}_m \to S$
be the projection, and
$p \colon \mathbb {G}_m \to S$
be the projection, and
![]() $T = {\mathbb {A}}^1/\mathbb {G}_m=\operatorname {\mathrm {Th}}_S(1)$
. Consider the composite (see (1.5))
$T = {\mathbb {A}}^1/\mathbb {G}_m=\operatorname {\mathrm {Th}}_S(1)$
. Consider the composite (see (1.5))
Then the following square is homotopy co-Cartesian in
![]() ${\mathrm{Spc}_{\bullet }}(S)[\eta ^{-1}]$
${\mathrm{Spc}_{\bullet }}(S)[\eta ^{-1}]$

Proof. From (2.1.3), we deduce a commutative diagram

where the left inner square is homotopy co-Cartesian. Applying (2.1.1) over the base
![]() $\mathbb {G}_m$
and using the functor
$\mathbb {G}_m$
and using the functor
![]() $p_\sharp $
of (1.9), we have in
$p_\sharp $
of (1.9), we have in
![]() $H_{\bullet }(S)$
$H_{\bullet }(S)$
It thus follows from (2.1.4) that the upper composite in the diagram (2.1.5.a) is an isomorphism in
![]() $H_{\bullet }(S)[\eta ^{-1}]$
, hence the exterior square in equation (2.1.5.a) is homotopy co-Cartesian. We conclude that the right inner square is homotopy co-Cartesian (by [Reference HirschhornHir03, Proposition 13.3.15, Remark 7.1.10]).
$H_{\bullet }(S)[\eta ^{-1}]$
, hence the exterior square in equation (2.1.5.a) is homotopy co-Cartesian. We conclude that the right inner square is homotopy co-Cartesian (by [Reference HirschhornHir03, Proposition 13.3.15, Remark 7.1.10]).
2.2 Global splitting
Definition 2.2.1. Let
![]() $L\to S$
be a line bundle. Denote by
$L\to S$
be a line bundle. Denote by
![]() $L^\circ $
the complement of the zero-section in L, and by
$L^\circ $
the complement of the zero-section in L, and by
![]() $p\colon L^{\circ } \to S$
the projection. Then the graph
$p\colon L^{\circ } \to S$
the projection. Then the graph
![]() $L^\circ \to L^\circ \times _S L$
of the open immersion
$L^\circ \to L^\circ \times _S L$
of the open immersion
![]() $L^\circ \to L$
may be viewed as a nowhere-vanishing section of the line bundle
$L^\circ \to L$
may be viewed as a nowhere-vanishing section of the line bundle
![]() $p^*L$
over
$p^*L$
over
![]() $L^\circ $
, which induces the tautological trivialisation
$L^\circ $
, which induces the tautological trivialisation
![]() $\tau \colon 1 \xrightarrow {\sim } p^*L$
. We define a morphism in
$\tau \colon 1 \xrightarrow {\sim } p^*L$
. We define a morphism in
![]() $H_{\bullet }(S)$
(recall that
$H_{\bullet }(S)$
(recall that
![]() $T=\operatorname {\mathrm {Th}}_S(1)$
, and see (1.5))
$T=\operatorname {\mathrm {Th}}_S(1)$
, and see (1.5))
Example 2.2.2. Assume that
![]() $L=1$
. Then the tautological trivialisation
$L=1$
. Then the tautological trivialisation
![]() $\tau \colon 1 \to 1$
of the trivial line bundle over
$\tau \colon 1 \to 1$
of the trivial line bundle over
![]() $L^\circ = \mathbb {G}_m$
is given by multiplication by the tautological section
$L^\circ = \mathbb {G}_m$
is given by multiplication by the tautological section
![]() $t \in H^0(\mathbb {G}_m,\mathbb {G}_m)$
, hence
$t \in H^0(\mathbb {G}_m,\mathbb {G}_m)$
, hence
![]() $\pi _1$
coincides with morphism
$\pi _1$
coincides with morphism
![]() $\pi $
of (2.1.5).
$\pi $
of (2.1.5).
2.2.3
Let
![]() $L\to S$
be a line bundle. If
$L\to S$
be a line bundle. If
![]() $f \colon R \to S$
is a scheme morphism, then the functor
$f \colon R \to S$
is a scheme morphism, then the functor
![]() $f^* \colon {\mathrm{Spc}_{\bullet }}(S) \to {\mathrm{Spc}_{\bullet }}(R)$
maps
$f^* \colon {\mathrm{Spc}_{\bullet }}(S) \to {\mathrm{Spc}_{\bullet }}(R)$
maps
![]() $\pi _L$
to
$\pi _L$
to
![]() $\pi _{f^*L}$
.
$\pi _{f^*L}$
.
2.2.4
If
![]() $\varphi \colon L \xrightarrow {\sim } M$
is an isomorphism of line bundles over S, then the following diagram commutes in
$\varphi \colon L \xrightarrow {\sim } M$
is an isomorphism of line bundles over S, then the following diagram commutes in
![]() $H_{\bullet }(S)$
$H_{\bullet }(S)$

Proposition 2.2.5. Let
![]() $L \to S$
be a line bundle. Then the following square is homotopy co-Cartesian in
$L \to S$
be a line bundle. Then the following square is homotopy co-Cartesian in
![]() ${\mathrm{Spc}_{\bullet }}(S)[\eta ^{-1}]$
${\mathrm{Spc}_{\bullet }}(S)[\eta ^{-1}]$

Proof. Let F be the homotopy colimit of the diagram
![]() $\operatorname {\mathrm {Th}}_S(L) \xleftarrow {\pi _L} T \wedge (L^\circ )_+ \xrightarrow {\operatorname {\mathrm {id}} \wedge p_+} T$
. By (1.10) and (1.9) (and in view of (2.2.3)), the fact that
$\operatorname {\mathrm {Th}}_S(L) \xleftarrow {\pi _L} T \wedge (L^\circ )_+ \xrightarrow {\operatorname {\mathrm {id}} \wedge p_+} T$
. By (1.10) and (1.9) (and in view of (2.2.3)), the fact that
![]() $F \simeq *$
may be verified Zariski locally on S. We may thus assume that L is trivial. By (2.2.4), we may further assume that
$F \simeq *$
may be verified Zariski locally on S. We may thus assume that L is trivial. By (2.2.4), we may further assume that
![]() $L=1$
so that
$L=1$
so that
![]() $L^\circ = \mathbb {G}_m$
. Then, in view of (2.2.2) the result follows from (2.1.5).
$L^\circ = \mathbb {G}_m$
. Then, in view of (2.2.2) the result follows from (2.1.5).
The next statement was initially inspired by [Reference LevineLev19, Proof of Theorem 4.1].
Corollary 2.2.6. Let
![]() $L \to S$
be a line bundle. Then in the notation of (2.2.1), we have an isomorphism in
$L \to S$
be a line bundle. Then in the notation of (2.2.1), we have an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
Proof. The square induced in
![]() $\operatorname {\mathrm {Spt}}(S)[\eta ^{-1}]$
by the square of (2.2.5) is homotopy co-Cartesian, hence also homotopy Cartesian (see, e.g., [Reference HoveyHov99, Remark 7.1.12]). This yields an isomorphism
$\operatorname {\mathrm {Spt}}(S)[\eta ^{-1}]$
by the square of (2.2.5) is homotopy co-Cartesian, hence also homotopy Cartesian (see, e.g., [Reference HoveyHov99, Remark 7.1.12]). This yields an isomorphism
from which the result follows by applying the functor
![]() $\Sigma ^{-2,-1}$
.
$\Sigma ^{-2,-1}$
.
Corollary 2.2.7. Let
![]() $L\to S$
be a line bundle and
$L\to S$
be a line bundle and
![]() $V \to S$
a vector bundle.
$V \to S$
a vector bundle.
-
(i) The natural map
 $\operatorname {\mathrm {Th}}_{L^\circ }(V) \to \operatorname {\mathrm {Th}}_S(V)$
extends to a natural isomorphism in
$\operatorname {\mathrm {Th}}_{L^\circ }(V) \to \operatorname {\mathrm {Th}}_S(V)$
extends to a natural isomorphism in
 $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
 $$\begin{align*}\operatorname{\mathrm{Th}}_{L^{\circ}}(V) \simeq \operatorname{\mathrm{Th}}_S(V) \oplus \Sigma^{-2,-1}\operatorname{\mathrm{Th}}_S(V \oplus L). \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Th}}_{L^{\circ}}(V) \simeq \operatorname{\mathrm{Th}}_S(V) \oplus \Sigma^{-2,-1}\operatorname{\mathrm{Th}}_S(V \oplus L). \end{align*}$$
-
(ii) Denote by
 $p \colon L^\circ \to S$
and
$p \colon L^\circ \to S$
and
 $p_1,p_2 \colon L^\circ \times _S L^\circ \to L^\circ $
the projections. Then
$p_1,p_2 \colon L^\circ \times _S L^\circ \to L^\circ $
the projections. Then  $$\begin{align*}\operatorname{\mathrm{Th}}_{L^\circ \times_S L^\circ}(V) \overset{p_1}{\underset{p_2}\rightrightarrows} \operatorname{\mathrm{Th}}_{L^\circ}(V) \xrightarrow{p} \operatorname{\mathrm{Th}}_S(V) \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Th}}_{L^\circ \times_S L^\circ}(V) \overset{p_1}{\underset{p_2}\rightrightarrows} \operatorname{\mathrm{Th}}_{L^\circ}(V) \xrightarrow{p} \operatorname{\mathrm{Th}}_S(V) \end{align*}$$
is a split coequaliser diagram in
 $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
Proof. Statement (i) follows by applying the autoequivalence
![]() $\Sigma ^V \colon \operatorname {\mathrm {SH}}(S)[\eta ^{-1}] \to \operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
to the decomposition of (2.2.6), in view of equation (1.3.b).
$\Sigma ^V \colon \operatorname {\mathrm {SH}}(S)[\eta ^{-1}] \to \operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
to the decomposition of (2.2.6), in view of equation (1.3.b).
Certainly in the diagram of equation (ii), we have
![]() $p \circ p_1 = p \circ p_2$
. The isomorphism (i) yields a section
$p \circ p_1 = p \circ p_2$
. The isomorphism (i) yields a section
![]() $s \colon \operatorname {\mathrm {Th}}_S(V) \to \operatorname {\mathrm {Th}}_{L^\circ }(V)$
of p in
$s \colon \operatorname {\mathrm {Th}}_S(V) \to \operatorname {\mathrm {Th}}_{L^\circ }(V)$
of p in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
. Then, in
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
. Then, in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, the composite
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, the composite
is a section of
On the other hand, in the commutative diagram in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
,
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
,

the upper composite is t, while the lower one is s. Therefore,
![]() $p_2 \circ t = s \circ p$
as endomorphisms of
$p_2 \circ t = s \circ p$
as endomorphisms of
![]() $\operatorname {\mathrm {Th}}_{L^\circ }(V)$
in
$\operatorname {\mathrm {Th}}_{L^\circ }(V)$
in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, proving equation (ii).
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, proving equation (ii).
Corollary 2.2.8. Let
![]() $L \to S$
be a line bundle, and denote by
$L \to S$
be a line bundle, and denote by
![]() $p \colon L^\circ \to S$
the projection. Then the functor
$p \colon L^\circ \to S$
the projection. Then the functor
![]() $p^* \colon \operatorname {\mathrm {SH}}(S)[\eta ^{-1}] \to \operatorname {\mathrm {SH}}(L^\circ )[\eta ^{-1}]$
is faithful and conservative.
$p^* \colon \operatorname {\mathrm {SH}}(S)[\eta ^{-1}] \to \operatorname {\mathrm {SH}}(L^\circ )[\eta ^{-1}]$
is faithful and conservative.
Proof. By the smooth projection formula and (2.2.6), the composite
![]() $p_\sharp \circ p^* {\colon} \operatorname {\mathrm {SH}}(S)[\eta ^{-1}] \kern1.3pt{\to} \operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
decomposes as
$p_\sharp \circ p^* {\colon} \operatorname {\mathrm {SH}}(S)[\eta ^{-1}] \kern1.3pt{\to} \operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
decomposes as
which is faithful, hence so is
![]() $p^*$
. The above formula also shows that
$p^*$
. The above formula also shows that
![]() $p_\sharp \circ p^*$
reflects zero-objects, hence so does
$p_\sharp \circ p^*$
reflects zero-objects, hence so does
![]() $p^*$
. Since
$p^*$
. Since
![]() $p^*$
is triangulated, it is conservative.
$p^*$
is triangulated, it is conservative.
Remark 2.2.9. The results of this section on line bundles will be generalised to odd rank vector bundles in §4.2.
3 Applications to twisted cohomology
3.1 Cohomology theories represented by ring spectra
3.1.1
Let
![]() $A \in \operatorname {\mathrm {Spt}}(S)$
be a motivic spectrum. For a pointed motivic space
$A \in \operatorname {\mathrm {Spt}}(S)$
be a motivic spectrum. For a pointed motivic space
![]() $\mathcal {X}$
, we write
$\mathcal {X}$
, we write
and
![]() $A^{*,*}(\mathcal {X}) = \bigoplus _{p,q\in \mathbb {Z}} A^{p,q}(\mathcal {X})$
. When X is a smooth S-scheme, we will write
$A^{*,*}(\mathcal {X}) = \bigoplus _{p,q\in \mathbb {Z}} A^{p,q}(\mathcal {X})$
. When X is a smooth S-scheme, we will write
![]() $A^{*,*}(X)$
instead of
$A^{*,*}(X)$
instead of
![]() $A^{*,*}(X_+)$
. If
$A^{*,*}(X_+)$
. If
![]() $E \to X$
is a vector bundle of constant rank r, we write
$E \to X$
is a vector bundle of constant rank r, we write
and extend this notation to arbitrary vector bundles in an obvious way. A morphism
![]() $f \colon \mathcal {Y} \to \mathcal {X}$
of pointed motivic spaces (resp. of smooth S-schemes) induces a pullback
$f \colon \mathcal {Y} \to \mathcal {X}$
of pointed motivic spaces (resp. of smooth S-schemes) induces a pullback
![]() $f^* \colon A^{*,*}(\mathcal {X}) \to A^{*,*}(\mathcal {Y})$
.
$f^* \colon A^{*,*}(\mathcal {X}) \to A^{*,*}(\mathcal {Y})$
.
3.1.2
A commutative ring spectrum will mean a commutative monoid in
![]() $(\operatorname {\mathrm {SH}}(S),\wedge ,\mathbf {1}_S)$
. When
$(\operatorname {\mathrm {SH}}(S),\wedge ,\mathbf {1}_S)$
. When
![]() $A \in \operatorname {\mathrm {SH}}(S)$
is a commutative ring spectrum and
$A \in \operatorname {\mathrm {SH}}(S)$
is a commutative ring spectrum and
![]() $X \in \operatorname {\mathrm {Sm}}_S$
, then
$X \in \operatorname {\mathrm {Sm}}_S$
, then
![]() $A^{*,*}(X)$
is naturally a ring, and
$A^{*,*}(X)$
is naturally a ring, and
![]() $A^{*,*}(X;E)$
an
$A^{*,*}(X;E)$
an
![]() $A^{*,*}(X)$
-module. When
$A^{*,*}(X)$
-module. When
![]() $u \in H^0(X,\mathbb {G}_m)$
, we will write
$u \in H^0(X,\mathbb {G}_m)$
, we will write
![]() $\langle u \rangle \in A^{0,0}(X)$
instead of
$\langle u \rangle \in A^{0,0}(X)$
instead of
![]() $\langle u \rangle ^*(1)$
(see (1.6)).
$\langle u \rangle ^*(1)$
(see (1.6)).
3.1.3
If A is an
![]() $\eta $
-periodic motivic spectrum, for any pointed motivic space
$\eta $
-periodic motivic spectrum, for any pointed motivic space
![]() $\mathcal {X}$
, we have natural isomorphisms for
$\mathcal {X}$
, we have natural isomorphisms for
![]() $p,q\in \mathbb {Z}$
$p,q\in \mathbb {Z}$
Proposition 3.1.4. Let A be an
![]() $\eta $
-periodic motivic spectrum. Let
$\eta $
-periodic motivic spectrum. Let
![]() $X \in \operatorname {\mathrm {Sm}}_S$
. Let
$X \in \operatorname {\mathrm {Sm}}_S$
. Let
![]() $L \to X$
be a line bundle and
$L \to X$
be a line bundle and
![]() $V \to X$
a vector bundle.
$V \to X$
a vector bundle.
-
(i) Denoting by
 $p \colon L^\circ \to X$
the projection, we have a split short exact sequence
$p \colon L^\circ \to X$
the projection, we have a split short exact sequence  $$\begin{align*}0 \to A^{*,*}(X;V) \xrightarrow{p^*} A^{*,*}(L^\circ;V) \to A^{*,*}(X;V \oplus L) \to 0. \end{align*}$$
$$\begin{align*}0 \to A^{*,*}(X;V) \xrightarrow{p^*} A^{*,*}(L^\circ;V) \to A^{*,*}(X;V \oplus L) \to 0. \end{align*}$$
-
(ii) Denoting by
 $p_1,p_2 \colon L^\circ \times _X L^\circ \to L^\circ $
the projections, we have an exact sequence
$p_1,p_2 \colon L^\circ \times _X L^\circ \to L^\circ $
the projections, we have an exact sequence  $$\begin{align*}0 \to A^{*,*}(X;V) \xrightarrow{p^*} A^{*,*}(L^\circ;V) \xrightarrow{p_1^*-p_2^*} A^{*,*}(L^\circ \times_X L^\circ;V). \end{align*}$$
$$\begin{align*}0 \to A^{*,*}(X;V) \xrightarrow{p^*} A^{*,*}(L^\circ;V) \xrightarrow{p_1^*-p_2^*} A^{*,*}(L^\circ \times_X L^\circ;V). \end{align*}$$
Proof. This follows by applying (2.2.7) over the base X to the image of A under the pullback
![]() $\operatorname {\mathrm {Spt}}(S) \to \operatorname {\mathrm {Spt}}(X)$
.
$\operatorname {\mathrm {Spt}}(S) \to \operatorname {\mathrm {Spt}}(X)$
.
3.2
 $\operatorname {\mathrm {SL}}$
- and
$\operatorname {\mathrm {SL}}$
- and
 $\operatorname {\mathrm {SL}}^c$
-orientations
$\operatorname {\mathrm {SL}}^c$
-orientations
Definition 3.2.1. An
![]() $\operatorname {\mathrm {SL}}$
-oriented vector bundle over a scheme X is a pair
$\operatorname {\mathrm {SL}}$
-oriented vector bundle over a scheme X is a pair
![]() $(E,\delta )$
, where
$(E,\delta )$
, where
![]() $E \to X$
is a vector bundle and
$E \to X$
is a vector bundle and
![]() $\delta \colon 1 \xrightarrow {\sim } \det E$
is an isomorphism of line bundles. We will also say that
$\delta \colon 1 \xrightarrow {\sim } \det E$
is an isomorphism of line bundles. We will also say that
![]() $\delta $
is an
$\delta $
is an
![]() $\operatorname {\mathrm {SL}}$
-orientation of the vector bundle
$\operatorname {\mathrm {SL}}$
-orientation of the vector bundle
![]() $E \to X$
. An isomorphism of
$E \to X$
. An isomorphism of
![]() $\operatorname {\mathrm {SL}}$
-oriented vector bundles
$\operatorname {\mathrm {SL}}$
-oriented vector bundles
![]() $(E,\delta ) \xrightarrow {\sim } (F,\epsilon )$
is an isomorphism of vector bundles
$(E,\delta ) \xrightarrow {\sim } (F,\epsilon )$
is an isomorphism of vector bundles
![]() $\varphi \colon E \xrightarrow {\sim } F$
such that
$\varphi \colon E \xrightarrow {\sim } F$
such that
![]() $(\det \varphi ) \circ \delta = \epsilon $
.
$(\det \varphi ) \circ \delta = \epsilon $
.
Definition 3.2.2 See [Reference Panin and WalterPW18, §3].
An
![]() $\operatorname {\mathrm {SL}}^c$
-oriented vector bundle over a scheme X is a triple
$\operatorname {\mathrm {SL}}^c$
-oriented vector bundle over a scheme X is a triple
![]() $(E,L,\lambda )$
, where
$(E,L,\lambda )$
, where
![]() $E \to X$
is a vector bundle and
$E \to X$
is a vector bundle and
![]() $L \to X$
a line bundle, and
$L \to X$
a line bundle, and
![]() $\lambda \colon L^{\otimes 2} \xrightarrow {\sim } \det E$
is an isomorphism. We will also say that
$\lambda \colon L^{\otimes 2} \xrightarrow {\sim } \det E$
is an isomorphism. We will also say that
![]() $(L,\lambda )$
is an
$(L,\lambda )$
is an
![]() $\operatorname {\mathrm {SL}}^c$
-orientation of the vector bundle
$\operatorname {\mathrm {SL}}^c$
-orientation of the vector bundle
![]() $E \to X$
. An isomorphism of
$E \to X$
. An isomorphism of
![]() $\operatorname {\mathrm {SL}}^c$
-oriented vector bundles
$\operatorname {\mathrm {SL}}^c$
-oriented vector bundles
![]() $(E,L,\lambda ) \xrightarrow {\sim } (F,M,\mu )$
is an isomorphism of vector bundles
$(E,L,\lambda ) \xrightarrow {\sim } (F,M,\mu )$
is an isomorphism of vector bundles
![]() $\varphi \colon E \xrightarrow {\sim } F$
and an isomorphism of line bundles
$\varphi \colon E \xrightarrow {\sim } F$
and an isomorphism of line bundles
![]() $\psi \colon L \xrightarrow {\sim } M$
such that
$\psi \colon L \xrightarrow {\sim } M$
such that
![]() $(\det \varphi ) \circ \lambda = \mu \circ \psi ^{\otimes 2}$
.
$(\det \varphi ) \circ \lambda = \mu \circ \psi ^{\otimes 2}$
.
3.2.3
Observe that each
![]() $\operatorname {\mathrm {SL}}$
-orientation
$\operatorname {\mathrm {SL}}$
-orientation
![]() $\delta $
of a vector bundle E induces an
$\delta $
of a vector bundle E induces an
![]() $\operatorname {\mathrm {SL}}^c$
-orientation
$\operatorname {\mathrm {SL}}^c$
-orientation
![]() $(L,\lambda )$
of E, where
$(L,\lambda )$
of E, where
![]() $L=1$
and
$L=1$
and
![]() $\lambda $
is the composite
$\lambda $
is the composite
![]() $1^{\otimes 2} \simeq 1 \xrightarrow {\delta } \det E$
.
$1^{\otimes 2} \simeq 1 \xrightarrow {\delta } \det E$
.
3.2.4
Let
![]() $(E,L,\lambda )$
be an
$(E,L,\lambda )$
be an
![]() $\operatorname {\mathrm {SL}}^c$
-oriented vector bundle, and assume that the line bundle L is trivial. Then every trivialisation
$\operatorname {\mathrm {SL}}^c$
-oriented vector bundle, and assume that the line bundle L is trivial. Then every trivialisation
![]() $\alpha \colon 1 \xrightarrow {\sim } L$
induces an
$\alpha \colon 1 \xrightarrow {\sim } L$
induces an
![]() $\operatorname {\mathrm {SL}}$
-orientation of E given by
$\operatorname {\mathrm {SL}}$
-orientation of E given by
Observe that the
![]() $\operatorname {\mathrm {SL}}^c$
-oriented vector bundle induced (in the sense of (3.2.3)) by
$\operatorname {\mathrm {SL}}^c$
-oriented vector bundle induced (in the sense of (3.2.3)) by
![]() $\delta _\alpha $
is isomorphic to
$\delta _\alpha $
is isomorphic to
![]() $(E,L,\lambda )$
.
$(E,L,\lambda )$
.
3.2.5
Consider a commutative ring spectrum
![]() $A \in \operatorname {\mathrm {SH}}(S)$
. By a
$A \in \operatorname {\mathrm {SH}}(S)$
. By a
![]() $\operatorname {\mathrm {SL}}$
-, resp.
$\operatorname {\mathrm {SL}}$
-, resp.
![]() $\operatorname {\mathrm {SL}}^c$
-, orientation of A, we will mean a normalised orientation in the sense of [Reference AnanyevskiyAna20, Definition 3.3]. Such data consists in Thom classes
$\operatorname {\mathrm {SL}}^c$
-, orientation of A, we will mean a normalised orientation in the sense of [Reference AnanyevskiyAna20, Definition 3.3]. Such data consists in Thom classes
![]() $\operatorname {\mathrm {th}}_{(E,\delta )} \in A^{*,*}(X;E)$
for each
$\operatorname {\mathrm {th}}_{(E,\delta )} \in A^{*,*}(X;E)$
for each
![]() $\operatorname {\mathrm {SL}}$
-oriented vector bundle
$\operatorname {\mathrm {SL}}$
-oriented vector bundle
![]() $(E,\delta )$
over
$(E,\delta )$
over
![]() $X \in \operatorname {\mathrm {Sm}}_S$
, resp.
$X \in \operatorname {\mathrm {Sm}}_S$
, resp.
![]() $\operatorname {\mathrm {th}}_{(E,L,\lambda )} \in A^{*,*}(X;E)$
for each
$\operatorname {\mathrm {th}}_{(E,L,\lambda )} \in A^{*,*}(X;E)$
for each
![]() $\operatorname {\mathrm {SL}}^c$
-oriented vector bundle
$\operatorname {\mathrm {SL}}^c$
-oriented vector bundle
![]() $(E,L,\lambda )$
over
$(E,L,\lambda )$
over
![]() $X \in \operatorname {\mathrm {Sm}}_S$
, satisfying a series of axioms.
$X \in \operatorname {\mathrm {Sm}}_S$
, satisfying a series of axioms.
3.2.6
Let
![]() $A \in \operatorname {\mathrm {SH}}(S)$
be a commutative ring spectrum. Then each
$A \in \operatorname {\mathrm {SH}}(S)$
be a commutative ring spectrum. Then each
![]() $\operatorname {\mathrm {SL}}^c$
-orientation of A induces an
$\operatorname {\mathrm {SL}}^c$
-orientation of A induces an
![]() $\operatorname {\mathrm {SL}}$
-orientation of A, by letting the Thom class of an
$\operatorname {\mathrm {SL}}$
-orientation of A, by letting the Thom class of an
![]() $\operatorname {\mathrm {SL}}$
-oriented vector bundle be the Thom class of the induced
$\operatorname {\mathrm {SL}}$
-oriented vector bundle be the Thom class of the induced
![]() $\operatorname {\mathrm {SL}}^c$
-oriented vector bundle, in the sense of (3.2.3).
$\operatorname {\mathrm {SL}}^c$
-oriented vector bundle, in the sense of (3.2.3).
Lemma 3.2.7. Let
![]() $A \in \operatorname {\mathrm {SH}}(S)$
be an
$A \in \operatorname {\mathrm {SH}}(S)$
be an
![]() $\operatorname {\mathrm {SL}}$
-oriented commutative ring spectrum. Let
$\operatorname {\mathrm {SL}}$
-oriented commutative ring spectrum. Let
![]() $(E,L,\lambda )$
be an
$(E,L,\lambda )$
be an
![]() $\operatorname {\mathrm {SL}}^c$
-oriented vector bundle over
$\operatorname {\mathrm {SL}}^c$
-oriented vector bundle over
![]() $X \in \operatorname {\mathrm {Sm}}_S$
, and assume that the line bundle L is trivial. Then, in the notation of (3.2.4), the Thom class
$X \in \operatorname {\mathrm {Sm}}_S$
, and assume that the line bundle L is trivial. Then, in the notation of (3.2.4), the Thom class
![]() $\operatorname {\mathrm {th}}_{(E,\delta _\alpha )} \in A^{*,*}(X;E)$
does not depend on the choice of the trivialisation
$\operatorname {\mathrm {th}}_{(E,\delta _\alpha )} \in A^{*,*}(X;E)$
does not depend on the choice of the trivialisation
![]() $\alpha $
of L.
$\alpha $
of L.
Proof. If
![]() $\alpha \colon 1 \xrightarrow {\sim } L$
is a trivialisation, then every trivialisation is of the form
$\alpha \colon 1 \xrightarrow {\sim } L$
is a trivialisation, then every trivialisation is of the form
![]() $u \alpha $
for some
$u \alpha $
for some
![]() $u \in H^0(X,\mathbb {G}_m)$
. In the notation of (3.2.4), we then have
$u \in H^0(X,\mathbb {G}_m)$
. In the notation of (3.2.4), we then have
![]() $\delta _{u \alpha } = u^2 \delta _{\alpha }$
. By [Reference AnanyevskiyAna20, Lemma 7.3], we have
$\delta _{u \alpha } = u^2 \delta _{\alpha }$
. By [Reference AnanyevskiyAna20, Lemma 7.3], we have
Since
![]() $\langle u^2 \rangle =1 \in A^{0,0}(X)$
by (2.1.1) (or [Reference AnanyevskiyAna20, Lemma 6.2]), the statement follows.
$\langle u^2 \rangle =1 \in A^{0,0}(X)$
by (2.1.1) (or [Reference AnanyevskiyAna20, Lemma 6.2]), the statement follows.
Proposition 3.2.8. Let
![]() $A \in \operatorname {\mathrm {SH}}(S)$
be an
$A \in \operatorname {\mathrm {SH}}(S)$
be an
![]() $\eta $
-periodic commutative ring spectrum. Then every
$\eta $
-periodic commutative ring spectrum. Then every
![]() $\operatorname {\mathrm {SL}}$
-orientation of A is induced (in the sense of (3.2.6)) by a unique
$\operatorname {\mathrm {SL}}$
-orientation of A is induced (in the sense of (3.2.6)) by a unique
![]() $\operatorname {\mathrm {SL}}^c$
-orientation.
$\operatorname {\mathrm {SL}}^c$
-orientation.
Proof. We assume given an
![]() $\operatorname {\mathrm {SL}}$
-orientation of A. Let
$\operatorname {\mathrm {SL}}$
-orientation of A. Let
![]() $(E,L,\lambda )$
be an
$(E,L,\lambda )$
be an
![]() $\operatorname {\mathrm {SL}}^c$
-oriented vector bundle. Denoting by
$\operatorname {\mathrm {SL}}^c$
-oriented vector bundle. Denoting by
![]() $p\colon L^\circ \to X$
the projection, the line bundle
$p\colon L^\circ \to X$
the projection, the line bundle
![]() $p^*L$
over
$p^*L$
over
![]() $L^\circ $
admits a tautological trivialisation
$L^\circ $
admits a tautological trivialisation
![]() $\tau \colon 1 \xrightarrow {\sim } p^*L$
. In view of (3.2.4), this yields an
$\tau \colon 1 \xrightarrow {\sim } p^*L$
. In view of (3.2.4), this yields an
![]() $\operatorname {\mathrm {SL}}$
-orientation
$\operatorname {\mathrm {SL}}$
-orientation
![]() $\delta _\tau $
of
$\delta _\tau $
of
![]() $p^*E$
.
$p^*E$
.
First, assume given an
![]() $\operatorname {\mathrm {SL}}^c$
-orientation of A compatible with its
$\operatorname {\mathrm {SL}}^c$
-orientation of A compatible with its
![]() $\operatorname {\mathrm {SL}}$
-orientation. As observed in (3.2.4), the
$\operatorname {\mathrm {SL}}$
-orientation. As observed in (3.2.4), the
![]() $\operatorname {\mathrm {SL}}^c$
-oriented vector bundle
$\operatorname {\mathrm {SL}}^c$
-oriented vector bundle
![]() $(p^*E,p^*L,p^*\lambda )$
is isomorphic to the one induced by the
$(p^*E,p^*L,p^*\lambda )$
is isomorphic to the one induced by the
![]() $\operatorname {\mathrm {SL}}$
-oriented vector bundle
$\operatorname {\mathrm {SL}}$
-oriented vector bundle
![]() $(p^*E,\delta _\tau )$
. Thus, we must have
$(p^*E,\delta _\tau )$
. Thus, we must have
Since
![]() $p^* \colon A^{*,*}(X;E) \to A^{*,*}(L^{\circ };p^*E)$
is injective by (3.1.4), we obtain the uniqueness part of the statement.
$p^* \colon A^{*,*}(X;E) \to A^{*,*}(L^{\circ };p^*E)$
is injective by (3.1.4), we obtain the uniqueness part of the statement.
We now construct an
![]() $\operatorname {\mathrm {SL}}^c$
-orientation of A from its
$\operatorname {\mathrm {SL}}^c$
-orientation of A from its
![]() $\operatorname {\mathrm {SL}}$
-orientation. In the situation considered at the beginning of the proof, let
$\operatorname {\mathrm {SL}}$
-orientation. In the situation considered at the beginning of the proof, let
![]() $p_1,p_2 \colon L^\circ \times _X L^\circ \to L^\circ $
be the projections, and set
$p_1,p_2 \colon L^\circ \times _X L^\circ \to L^\circ $
be the projections, and set
![]() $q=p \circ p_1=p \circ p_2$
. The tautological trivialisation
$q=p \circ p_1=p \circ p_2$
. The tautological trivialisation
![]() $\tau $
of
$\tau $
of
![]() $p^*L$
yields two trivialisations
$p^*L$
yields two trivialisations
![]() $p_1^*\tau $
and
$p_1^*\tau $
and
![]() $p_2^*\tau $
of
$p_2^*\tau $
of
![]() $q^*L$
, and thus two
$q^*L$
, and thus two
![]() $\operatorname {\mathrm {SL}}$
-orientations
$\operatorname {\mathrm {SL}}$
-orientations
![]() $\alpha _1=\delta _{p_1^*\tau }$
and
$\alpha _1=\delta _{p_1^*\tau }$
and
![]() $\alpha _2=\delta _{p_2^*\tau }$
of E. However, it follows from (3.2.7) that their Thom classes coincide so that (observe that
$\alpha _2=\delta _{p_2^*\tau }$
of E. However, it follows from (3.2.7) that their Thom classes coincide so that (observe that
![]() $\alpha _i = p_i^*(\delta _\tau )$
for
$\alpha _i = p_i^*(\delta _\tau )$
for
![]() $i=1,2$
)
$i=1,2$
)
Therefore, it follows from (3.1.4.ii) that the element
![]() $\operatorname {\mathrm {th}}_{(p^*E,\delta _\tau )} \in A^{*,*}(L^\circ ;E)$
is the image of a unique element
$\operatorname {\mathrm {th}}_{(p^*E,\delta _\tau )} \in A^{*,*}(L^\circ ;E)$
is the image of a unique element
![]() $\theta _{(E,L,\lambda )} \in A^{*,*}(X;E)$
.
$\theta _{(E,L,\lambda )} \in A^{*,*}(X;E)$
.
From the fact that
![]() $(E,\delta ) \mapsto \operatorname {\mathrm {th}}_{(E,\delta )}$
defines an
$(E,\delta ) \mapsto \operatorname {\mathrm {th}}_{(E,\delta )}$
defines an
![]() $\operatorname {\mathrm {SL}}$
-orientation of A, we deduce at once that
$\operatorname {\mathrm {SL}}$
-orientation of A, we deduce at once that
![]() $(E,L,\lambda ) \mapsto \theta _{(E,L,\lambda )}$
defines an
$(E,L,\lambda ) \mapsto \theta _{(E,L,\lambda )}$
defines an
![]() $\operatorname {\mathrm {SL}}^c$
-orientation of A: Indeed, each axiom of [Reference AnanyevskiyAna20, Definition 3.3] can be verified after pulling back along
$\operatorname {\mathrm {SL}}^c$
-orientation of A: Indeed, each axiom of [Reference AnanyevskiyAna20, Definition 3.3] can be verified after pulling back along
![]() $p\colon L^\circ \to X$
since
$p\colon L^\circ \to X$
since
![]() $p^* \colon A^{*,*}(X;E) \to A^{*,*}(L^\circ ;p^*E)$
is injective by (3.1.4).
$p^* \colon A^{*,*}(X;E) \to A^{*,*}(L^\circ ;p^*E)$
is injective by (3.1.4).
To conclude the proof, it remains to show the
![]() $\operatorname {\mathrm {SL}}^c$
-orientation
$\operatorname {\mathrm {SL}}^c$
-orientation
![]() $(E,L,\lambda ) \mapsto \theta _{(E,L,\lambda )}$
induces the original
$(E,L,\lambda ) \mapsto \theta _{(E,L,\lambda )}$
induces the original
![]() $\operatorname {\mathrm {SL}}$
-orientation of A. So let us assume that the
$\operatorname {\mathrm {SL}}$
-orientation of A. So let us assume that the
![]() $\operatorname {\mathrm {SL}}^c$
-oriented vector bundle
$\operatorname {\mathrm {SL}}^c$
-oriented vector bundle
![]() $(E,L,\lambda )$
is induced by an
$(E,L,\lambda )$
is induced by an
![]() $\operatorname {\mathrm {SL}}$
-oriented vector bundle
$\operatorname {\mathrm {SL}}$
-oriented vector bundle
![]() $(E,\delta )$
, in the sense of (3.2.3). In particular,
$(E,\delta )$
, in the sense of (3.2.3). In particular,
![]() $L=1$
. Then the tautological trivialisation
$L=1$
. Then the tautological trivialisation
![]() $\tau \colon 1 \xrightarrow {\sim } p^*L$
and the trivialisation
$\tau \colon 1 \xrightarrow {\sim } p^*L$
and the trivialisation
![]() $1 =p^*1 =p^*L$
yield two
$1 =p^*1 =p^*L$
yield two
![]() $\operatorname {\mathrm {SL}}$
-orientations of
$\operatorname {\mathrm {SL}}$
-orientations of
![]() $p^*E$
. Their Thom classes in
$p^*E$
. Their Thom classes in
![]() $A^{*,*}(L^\circ ;p^*E)$
coincide by (3.2.7), and they are, respectively,
$A^{*,*}(L^\circ ;p^*E)$
coincide by (3.2.7), and they are, respectively,
![]() $p^*\theta _{(E,L,\lambda )}$
and
$p^*\theta _{(E,L,\lambda )}$
and
![]() $p^*\operatorname {\mathrm {th}}_{(E,\delta )}$
. Since
$p^*\operatorname {\mathrm {th}}_{(E,\delta )}$
. Since
![]() $p^* \colon A^{*,*}(X;E) \to A^{*,*}(L^\circ ;p^*E)$
is injective by (3.1.4), we have
$p^* \colon A^{*,*}(X;E) \to A^{*,*}(L^\circ ;p^*E)$
is injective by (3.1.4), we have
![]() $\theta _{(E,L,\lambda )} = \operatorname {\mathrm {th}}_{(E,\delta )} \in A^{*,*}(X;E)$
, as required.
$\theta _{(E,L,\lambda )} = \operatorname {\mathrm {th}}_{(E,\delta )} \in A^{*,*}(X;E)$
, as required.
Remark 3.2.9. Ananyevskiy constructed ‘Thom isomorphisms’ associated with
![]() $\operatorname {\mathrm {SL}}^c$
-bundles in [Reference AnanyevskiyAna20, §4] when A is an arbitrary
$\operatorname {\mathrm {SL}}^c$
-bundles in [Reference AnanyevskiyAna20, §4] when A is an arbitrary
![]() $\operatorname {\mathrm {SL}}$
-oriented theory, but as explained in [Reference AnanyevskiyAna20, Remark 4.4] it is not clear whether this yields an
$\operatorname {\mathrm {SL}}$
-oriented theory, but as explained in [Reference AnanyevskiyAna20, Remark 4.4] it is not clear whether this yields an
![]() $\operatorname {\mathrm {SL}}^c$
-orientation, the problem being the multiplicativity axiom. When A is
$\operatorname {\mathrm {SL}}^c$
-orientation, the problem being the multiplicativity axiom. When A is
![]() $\eta $
-periodic, our construction leads to the same Thom isomorphisms for
$\eta $
-periodic, our construction leads to the same Thom isomorphisms for
![]() $\operatorname {\mathrm {SL}}^c$
-bundles (in fact, the proof of (3.2.8) shows that there is at most one way to construct such functorial isomorphisms compatibly with the
$\operatorname {\mathrm {SL}}^c$
-bundles (in fact, the proof of (3.2.8) shows that there is at most one way to construct such functorial isomorphisms compatibly with the
![]() $\operatorname {\mathrm {SL}}$
-orientation). Thus, the Thom isomorphisms constructed by Ananyevskiy do give rise to an
$\operatorname {\mathrm {SL}}$
-orientation). Thus, the Thom isomorphisms constructed by Ananyevskiy do give rise to an
![]() $\operatorname {\mathrm {SL}}^c$
-orientation when A is
$\operatorname {\mathrm {SL}}^c$
-orientation when A is
![]() $\eta $
-periodic.
$\eta $
-periodic.
3.3 Twisting by doubles and squares of line bundles
Proposition 3.3.1. Let L be a line bundle over S.
-
(i) There exist an isomorphism
 $\Sigma ^{4,2}\mathbf {1}_S \simeq \operatorname {\mathrm {Th}}_S(L^{\oplus 2})$
in
$\Sigma ^{4,2}\mathbf {1}_S \simeq \operatorname {\mathrm {Th}}_S(L^{\oplus 2})$
in
 $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
. -
(ii) If
 $s_1,s_2 \in \mathbb {Z}$
are of the same parity, there exist an isomorphism
$s_1,s_2 \in \mathbb {Z}$
are of the same parity, there exist an isomorphism  $$\begin{align*}\operatorname{\mathrm{Th}}_S(L^{\otimes s_1}) \simeq \operatorname{\mathrm{Th}}_S(L^{\otimes s_2}) \; \text{in } \operatorname{\mathrm{SH}}(S)[\eta^{-1}]. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Th}}_S(L^{\otimes s_1}) \simeq \operatorname{\mathrm{Th}}_S(L^{\otimes s_2}) \; \text{in } \operatorname{\mathrm{SH}}(S)[\eta^{-1}]. \end{align*}$$
Proof. Let us first assume that the line bundle
![]() $L \to S$
admits a trivialisation
$L \to S$
admits a trivialisation
![]() $\alpha \colon 1 \xrightarrow {\sim } L$
. Then we have an isomorphism in
$\alpha \colon 1 \xrightarrow {\sim } L$
. Then we have an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)$
(see (1.5))
$\operatorname {\mathrm {SH}}(S)$
(see (1.5))
Every trivialisation of L is of the form
![]() $u \alpha $
with
$u \alpha $
with
![]() $u \in H^0(S,\mathbb {G}_m)$
. As automorphisms of
$u \in H^0(S,\mathbb {G}_m)$
. As automorphisms of
![]() $\operatorname {\mathrm {Th}}_S(1^{\oplus 2})$
in
$\operatorname {\mathrm {Th}}_S(1^{\oplus 2})$
in
![]() $\operatorname {\mathrm {SH}}(S)$
we have,
$\operatorname {\mathrm {SH}}(S)$
we have,
because
![]() $\operatorname {\mathrm {Th}}((u^{-1}\operatorname {\mathrm {id}}_1) \oplus (u\operatorname {\mathrm {id}}_1))$
is the identity of
$\operatorname {\mathrm {Th}}((u^{-1}\operatorname {\mathrm {id}}_1) \oplus (u\operatorname {\mathrm {id}}_1))$
is the identity of
![]() $\operatorname {\mathrm {Th}}_S(1^{\oplus 2})$
, being given by a product of transvections (see the proof of (2.1.1)). Now, by (2.1.1), under the identification
$\operatorname {\mathrm {Th}}_S(1^{\oplus 2})$
, being given by a product of transvections (see the proof of (2.1.1)). Now, by (2.1.1), under the identification
![]() $\operatorname {\mathrm {Th}}_S(1^{\oplus 2})=\operatorname {\mathrm {Th}}_S(1) \wedge \operatorname {\mathrm {Th}}_S(1)$
(see equation (1.3.b)), we have
$\operatorname {\mathrm {Th}}_S(1^{\oplus 2})=\operatorname {\mathrm {Th}}_S(1) \wedge \operatorname {\mathrm {Th}}_S(1)$
(see equation (1.3.b)), we have
Therefore,
![]() $\operatorname {\mathrm {Th}}((u\operatorname {\mathrm {id}}_1)^{\oplus 2})$
is the identity of
$\operatorname {\mathrm {Th}}((u\operatorname {\mathrm {id}}_1)^{\oplus 2})$
is the identity of
![]() $\operatorname {\mathrm {Th}}_S(1^{\oplus 2})$
in
$\operatorname {\mathrm {Th}}_S(1^{\oplus 2})$
in
![]() $\operatorname {\mathrm {SH}}(S)$
, hence
$\operatorname {\mathrm {SH}}(S)$
, hence
so that the isomorphism
![]() $\operatorname {\mathrm {Th}}(\alpha ^{\oplus 2})$
in
$\operatorname {\mathrm {Th}}(\alpha ^{\oplus 2})$
in
![]() $\operatorname {\mathrm {SH}}(S)$
considered in equation (3.3.1.a) is independent of the choice of the trivialisation
$\operatorname {\mathrm {SH}}(S)$
considered in equation (3.3.1.a) is independent of the choice of the trivialisation
![]() $\alpha $
.
$\alpha $
.
Next, let us consider the case (ii). If
![]() $\alpha \colon 1 \xrightarrow {\sim } L$
is a trivialisation, we have an isomorphism in
$\alpha \colon 1 \xrightarrow {\sim } L$
is a trivialisation, we have an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)$
$\operatorname {\mathrm {SH}}(S)$
(Here and below, for
![]() $r \in \mathbb {N}$
, the notation
$r \in \mathbb {N}$
, the notation
![]() $\alpha ^{\otimes -r}$
refers to the morphism
$\alpha ^{\otimes -r}$
refers to the morphism
![]() $((\alpha ^\vee )^{-1})^{\otimes r}$
.) Now for
$((\alpha ^\vee )^{-1})^{\otimes r}$
.) Now for
![]() $u \in H^0(S,\mathbb {G}_m)$
, the composite in
$u \in H^0(S,\mathbb {G}_m)$
, the composite in
![]() $\operatorname {\mathrm {SH}}(S)$
$\operatorname {\mathrm {SH}}(S)$
coincides with
![]() $\operatorname {\mathrm {Th}}(u^{s_2-s_1} \operatorname {\mathrm {id}}_1)$
, which is the identity by (2.1.1) (recall that
$\operatorname {\mathrm {Th}}(u^{s_2-s_1} \operatorname {\mathrm {id}}_1)$
, which is the identity by (2.1.1) (recall that
![]() $s_2-s_1$
is even), and in particular does not depend on
$s_2-s_1$
is even), and in particular does not depend on
![]() $u\in H^0(S,\mathbb {G}_m)$
. Since the left and right arrows in the above composite are isomorphisms, we deduce that the middle arrow does not depend on
$u\in H^0(S,\mathbb {G}_m)$
. Since the left and right arrows in the above composite are isomorphisms, we deduce that the middle arrow does not depend on
![]() $u\in H^0(S,\mathbb {G}_m)$
, which shows as above that the isomorphism (3.3.1.b) is independent of the choice of the trivialisation
$u\in H^0(S,\mathbb {G}_m)$
, which shows as above that the isomorphism (3.3.1.b) is independent of the choice of the trivialisation
![]() $\alpha $
.
$\alpha $
.
Let us come back to the general case, where
![]() $L \to S$
is a possibly nontrivial line bundle. Let
$L \to S$
is a possibly nontrivial line bundle. Let
![]() $p\colon L^\circ \to S$
be the projection, and consider the tautological trivialisation
$p\colon L^\circ \to S$
be the projection, and consider the tautological trivialisation
![]() $\tau $
of the line bundle
$\tau $
of the line bundle
![]() $p^*L$
over
$p^*L$
over
![]() $L^\circ $
. Let us consider the isomorphism
$L^\circ $
. Let us consider the isomorphism
![]() $\varphi \colon \operatorname {\mathrm {Th}}_{L^\circ }(B) \xrightarrow {\sim } \operatorname {\mathrm {Th}}_{L^\circ }(C)$
in
$\varphi \colon \operatorname {\mathrm {Th}}_{L^\circ }(B) \xrightarrow {\sim } \operatorname {\mathrm {Th}}_{L^\circ }(C)$
in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, where
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, where
-
•
 $B = 1^{\oplus 2}, C=L^{\oplus 2}, \varphi = \operatorname {\mathrm {Th}}(\tau ^{\oplus 2})$
in case (i).
$B = 1^{\oplus 2}, C=L^{\oplus 2}, \varphi = \operatorname {\mathrm {Th}}(\tau ^{\oplus 2})$
in case (i). -
•
 $B = L^{\otimes s_1}, C=L^{\otimes s_2}, \varphi = \operatorname {\mathrm {Th}}(\operatorname {\mathrm {id}}_{L^{\otimes s_1}} \otimes \alpha ^{\otimes s_2-s_1})$
in case (ii).
$B = L^{\otimes s_1}, C=L^{\otimes s_2}, \varphi = \operatorname {\mathrm {Th}}(\operatorname {\mathrm {id}}_{L^{\otimes s_1}} \otimes \alpha ^{\otimes s_2-s_1})$
in case (ii).
Let
![]() $p_1,p_2 \colon L^\circ \times _S L^\circ \to L^\circ $
be the projections, and set
$p_1,p_2 \colon L^\circ \times _S L^\circ \to L^\circ $
be the projections, and set
![]() $q=p \circ p_1=p \circ p_2$
. For
$q=p \circ p_1=p \circ p_2$
. For
![]() $i\in \{1,2\}$
, the isomorphism
$i\in \{1,2\}$
, the isomorphism
![]() $p_i^*\varphi \colon \operatorname {\mathrm {Th}}_{L^\circ \times _S L^\circ }(B) \to \operatorname {\mathrm {Th}}_{L^\circ \times _S L^\circ }(C)$
in
$p_i^*\varphi \colon \operatorname {\mathrm {Th}}_{L^\circ \times _S L^\circ }(B) \to \operatorname {\mathrm {Th}}_{L^\circ \times _S L^\circ }(C)$
in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
is induced by the trivialisation
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
is induced by the trivialisation
![]() $p_i^*\tau $
of the line bundle
$p_i^*\tau $
of the line bundle
![]() $q^*L$
over
$q^*L$
over
![]() $L^\circ \times _S L^\circ $
, hence does not depend on i, by the special case considered at the beginning of the proof. Thus, by (2.2.7.ii) there exists a unique morphism f fitting into the commutative diagram in
$L^\circ \times _S L^\circ $
, hence does not depend on i, by the special case considered at the beginning of the proof. Thus, by (2.2.7.ii) there exists a unique morphism f fitting into the commutative diagram in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$

as well as a unique morphism g into the commutative diagram in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$

As
![]() $p \colon \operatorname {\mathrm {Th}}_{L^{\circ }}(B) \to \operatorname {\mathrm {Th}}_S(B)$
and
$p \colon \operatorname {\mathrm {Th}}_{L^{\circ }}(B) \to \operatorname {\mathrm {Th}}_S(B)$
and
![]() $p \colon \operatorname {\mathrm {Th}}_{L^{\circ }}(C) \to \operatorname {\mathrm {Th}}_S(C)$
are epimorphisms in
$p \colon \operatorname {\mathrm {Th}}_{L^{\circ }}(C) \to \operatorname {\mathrm {Th}}_S(C)$
are epimorphisms in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
(see (2.2.7)), it follows that f and g are mutually inverse isomorphisms in
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
(see (2.2.7)), it follows that f and g are mutually inverse isomorphisms in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
4 Nowhere-vanishing sections of odd rank bundles
4.1 Projective bundles
The results of this section are slight generalisations of those of [Reference AnanyevskiyAna16a, §4].
4.1.1
Let us consider the linear embeddings
![]() $i_k \colon \mathbb {P}^k \to \mathbb {P}^{k+1}$
given by the vanishing of the last coordinate. Denote by
$i_k \colon \mathbb {P}^k \to \mathbb {P}^{k+1}$
given by the vanishing of the last coordinate. Denote by
![]() $\iota _k \colon S \to \mathbb {P}^k$
the S-point given by the composite
$\iota _k \colon S \to \mathbb {P}^k$
the S-point given by the composite
![]() ${S=\mathbb {P}^0 \xrightarrow {i_0} \mathbb {P}^1 \xrightarrow {i_1} \cdots \xrightarrow {i_{k-1}} \mathbb {P}^k}$
.
${S=\mathbb {P}^0 \xrightarrow {i_0} \mathbb {P}^1 \xrightarrow {i_1} \cdots \xrightarrow {i_{k-1}} \mathbb {P}^k}$
.
4.1.2
Assume given a collection
![]() $\mathcal {D}=(d_1,\ldots ,d_r) \in \mathbb {Z}^r$
for some
$\mathcal {D}=(d_1,\ldots ,d_r) \in \mathbb {Z}^r$
for some
![]() $r\in \mathbb {N}$
. We will denote by
$r\in \mathbb {N}$
. We will denote by
![]() $\mathcal {O}(\mathcal {D})$
the vector bundle
$\mathcal {O}(\mathcal {D})$
the vector bundle
![]() $\mathcal {O}(d_1) \oplus \cdots \oplus \mathcal {O}(d_r)$
over
$\mathcal {O}(d_1) \oplus \cdots \oplus \mathcal {O}(d_r)$
over
![]() $\mathbb {P}^k$
, for each
$\mathbb {P}^k$
, for each
![]() $k \in \mathbb {N}$
. When
$k \in \mathbb {N}$
. When
![]() $k=0$
, we have a canonical isomorphism
$k=0$
, we have a canonical isomorphism
![]() $\mathcal {O}(\mathcal {D}) \simeq 1^{\oplus r}$
over
$\mathcal {O}(\mathcal {D}) \simeq 1^{\oplus r}$
over
![]() $\mathbb {P}^0=S$
. This yields, for any
$\mathbb {P}^0=S$
. This yields, for any
![]() $k\in \mathbb {N}$
, a canonical map in
$k\in \mathbb {N}$
, a canonical map in
![]() $\operatorname {\mathrm {Spt}}(S)$
$\operatorname {\mathrm {Spt}}(S)$
Proposition 4.1.3. Let
![]() $k,r \in \mathbb {N}$
, and
$k,r \in \mathbb {N}$
, and
![]() $d_1,\ldots ,d_r \in \mathbb {Z}$
. Set
$d_1,\ldots ,d_r \in \mathbb {Z}$
. Set
![]() $\mathcal {D}=(d_1,\ldots ,d_r)$
, and let
$\mathcal {D}=(d_1,\ldots ,d_r)$
, and let
![]() ${d=d_1 +\cdots +d_r}$
. We use the notation
${d=d_1 +\cdots +d_r}$
. We use the notation
![]() $\mathcal {O}(\mathcal {D})$
described in (4.1.2).
$\mathcal {O}(\mathcal {D})$
described in (4.1.2).
-
(i) If k and d are odd, then
 $\operatorname {\mathrm {Th}}_{\mathbb {P}^k}(\mathcal {O}(\mathcal {D})) = 0$
in
$\operatorname {\mathrm {Th}}_{\mathbb {P}^k}(\mathcal {O}(\mathcal {D})) = 0$
in
 $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
. -
(ii) If k and d are even, then equation (4.1.2.a) induces an isomorphism
 $\Sigma ^{2r,r}\mathbf {1}_S \simeq \operatorname {\mathrm {Th}}_{\mathbb {P}^k}(\mathcal {O}(\mathcal {D}))$
in
$\Sigma ^{2r,r}\mathbf {1}_S \simeq \operatorname {\mathrm {Th}}_{\mathbb {P}^k}(\mathcal {O}(\mathcal {D}))$
in
 $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
. -
(iii) If k is even and d is odd, then
 $\operatorname {\mathrm {Th}}_{\mathbb {P}^k}(\mathcal {O}(\mathcal {D})) \simeq \Sigma ^{2(k+r),k+r}\mathbf {1}_S$
.
$\operatorname {\mathrm {Th}}_{\mathbb {P}^k}(\mathcal {O}(\mathcal {D})) \simeq \Sigma ^{2(k+r),k+r}\mathbf {1}_S$
. -
(iv) If k is odd and d is even, then
 $\operatorname {\mathrm {Th}}_{\mathbb {P}^k}(\mathcal {O}(\mathcal {D})) \simeq \Sigma ^{2(k+r),k+r}\mathbf {1}_S \oplus \Sigma ^{2r,r}\mathbf {1}_S$
.
$\operatorname {\mathrm {Th}}_{\mathbb {P}^k}(\mathcal {O}(\mathcal {D})) \simeq \Sigma ^{2(k+r),k+r}\mathbf {1}_S \oplus \Sigma ^{2r,r}\mathbf {1}_S$
.
Proof. Let us first prove (i). Assume that k and d are odd. Consider a linear embedding
![]() $\mathbb {P}^1 \to \mathbb {P}^k$
. Its normal bundle is
$\mathbb {P}^1 \to \mathbb {P}^k$
. Its normal bundle is
![]() $\mathcal {O}(1)^{\oplus k-1}$
, and its open complement is a vector bundle over
$\mathcal {O}(1)^{\oplus k-1}$
, and its open complement is a vector bundle over
![]() $\mathbb {P}^{k-2}$
. The corresponding zero-section
$\mathbb {P}^{k-2}$
. The corresponding zero-section
![]() $\mathbb {P}^{k-2} \to \mathbb {P}^k\smallsetminus \mathbb {P}^1$
induces an isomorphism in
$\mathbb {P}^{k-2} \to \mathbb {P}^k\smallsetminus \mathbb {P}^1$
induces an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)$
and is the restriction of a linear embedding
$\operatorname {\mathrm {SH}}(S)$
and is the restriction of a linear embedding
![]() $\mathbb {P}^{k-2} \to \mathbb {P}^k$
. Thus, (1.4) yields a distinguished triangle in
$\mathbb {P}^{k-2} \to \mathbb {P}^k$
. Thus, (1.4) yields a distinguished triangle in
![]() $\operatorname {\mathrm {SH}}(S)$
$\operatorname {\mathrm {SH}}(S)$
Using induction on the odd integer k, we are reduced to assuming that
![]() $k=1$
. Now, by (3.3.1.ii) we have in
$k=1$
. Now, by (3.3.1.ii) we have in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
where s is the number of indices
![]() $i \in \{1,\dots ,r\}$
such that
$i \in \{1,\dots ,r\}$
such that
![]() $d_i$
is even. Since d is odd, so is
$d_i$
is even. Since d is odd, so is
![]() $r-s$
and using (3.3.1.i), we deduce that
$r-s$
and using (3.3.1.i), we deduce that
But
![]() $\operatorname {\mathrm {Th}}_{\mathbb {P}^1}(\mathcal {O}(-1))$
vanishes in
$\operatorname {\mathrm {Th}}_{\mathbb {P}^1}(\mathcal {O}(-1))$
vanishes in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
because of the distinguished triangle (see (1.3.a))
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
because of the distinguished triangle (see (1.3.a))
and the definition of the map
![]() $\eta $
(recall that
$\eta $
(recall that
![]() $\mathcal {O}(-1)^\circ = {\mathbb {A}}^2 \smallsetminus \{0\}$
). We have proved equation (i).
$\mathcal {O}(-1)^\circ = {\mathbb {A}}^2 \smallsetminus \{0\}$
). We have proved equation (i).
Let us come back to the situation when k and d are arbitrary. Consider a linear embedding
![]() $\mathbb {P}^{k-1} \to \mathbb {P}^k$
avoiding the S-point
$\mathbb {P}^{k-1} \to \mathbb {P}^k$
avoiding the S-point
![]() $\iota _k \colon S \to \mathbb {P}^k$
(we write
$\iota _k \colon S \to \mathbb {P}^k$
(we write
![]() $\mathbb {P}^{-1}=\varnothing $
). It is a closed immersion defined by the vanishing of a regular section of
$\mathbb {P}^{-1}=\varnothing $
). It is a closed immersion defined by the vanishing of a regular section of
![]() $\mathcal {O}(1)$
. Its open complement is isomorphic to
$\mathcal {O}(1)$
. Its open complement is isomorphic to
![]() ${\mathbb {A}}^k$
, and the morphism
${\mathbb {A}}^k$
, and the morphism
![]() $j_k\colon S \to {\mathbb {A}}^k$
induced by
$j_k\colon S \to {\mathbb {A}}^k$
induced by
![]() $\iota _k$
induces an isomorphism in
$\iota _k$
induces an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)$
. The canonical trivialisation of
$\operatorname {\mathrm {SH}}(S)$
. The canonical trivialisation of
![]() $\mathcal {O}(\mathcal {D})$
over
$\mathcal {O}(\mathcal {D})$
over
![]() $\mathbb {P}^0=S$
is the restriction along
$\mathbb {P}^0=S$
is the restriction along
![]() $j_k$
of a trivialisation of
$j_k$
of a trivialisation of
![]() $\mathcal {O}(\mathcal {D})|_{{\mathbb {A}}^k}$
(induced by the trivialisation of
$\mathcal {O}(\mathcal {D})|_{{\mathbb {A}}^k}$
(induced by the trivialisation of
![]() $\mathcal {O}(1)|_{{\mathbb {A}}^k}$
corresponding to the regular section of
$\mathcal {O}(1)|_{{\mathbb {A}}^k}$
corresponding to the regular section of
![]() $\mathcal {O}(1)$
mentioned above). It follows that the map
$\mathcal {O}(1)$
mentioned above). It follows that the map
![]() $\operatorname {\mathrm {Th}}_{\mathbb {P}^0}(\mathcal {O}(\mathcal {D})) \to \operatorname {\mathrm {Th}}_{{\mathbb {A}}^k}(\mathcal {O}(\mathcal {D}))$
induced by
$\operatorname {\mathrm {Th}}_{\mathbb {P}^0}(\mathcal {O}(\mathcal {D})) \to \operatorname {\mathrm {Th}}_{{\mathbb {A}}^k}(\mathcal {O}(\mathcal {D}))$
induced by
![]() $j_k$
induces an isomorphism in
$j_k$
induces an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)$
. Thus, (1.4) yields a distinguished triangle in
$\operatorname {\mathrm {SH}}(S)$
. Thus, (1.4) yields a distinguished triangle in
![]() $\operatorname {\mathrm {SH}}(S)$
$\operatorname {\mathrm {SH}}(S)$
so that equation (ii) follows from equation (i).
Consider now a linear embedding
![]() $s\colon S=\mathbb {P}^0 \to \mathbb {P}^k$
avoiding
$s\colon S=\mathbb {P}^0 \to \mathbb {P}^k$
avoiding
![]() $i_{k-1}(\mathbb {P}^{k-1})$
. Its open complement U is a line bundle over
$i_{k-1}(\mathbb {P}^{k-1})$
. Its open complement U is a line bundle over
![]() $\mathbb {P}^{k-1}$
. The corresponding zero-section
$\mathbb {P}^{k-1}$
. The corresponding zero-section
![]() $\mathbb {P}^{k-1} \to U$
induces an isomorphism in
$\mathbb {P}^{k-1} \to U$
induces an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)$
and is the restriction of the linear embedding
$\operatorname {\mathrm {SH}}(S)$
and is the restriction of the linear embedding
![]() $i_{k-1} \colon \mathbb {P}^{k-1} \to \mathbb {P}^k$
. Since the vector bundle
$i_{k-1} \colon \mathbb {P}^{k-1} \to \mathbb {P}^k$
. Since the vector bundle
![]() $s^*\mathcal {O}(\mathcal {D})$
and the normal bundle
$s^*\mathcal {O}(\mathcal {D})$
and the normal bundle
![]() $s^*\mathcal {O}(1)^{\oplus k}$
to s are both trivial, we have by (1.4) a distinguished triangle in
$s^*\mathcal {O}(1)^{\oplus k}$
to s are both trivial, we have by (1.4) a distinguished triangle in
![]() $\operatorname {\mathrm {SH}}(S)$
$\operatorname {\mathrm {SH}}(S)$
Therefore, equation (iii) follows from equation (i).
Finally, assume that k is odd and d is even. It follows from equation (ii) that the composite
![]() $\operatorname {\mathrm {Th}}_{\mathbb {P}^{k-1}}(\mathcal {O}(\mathcal {D})) \to \operatorname {\mathrm {Th}}_{\mathbb {P}^k}(\mathcal {O}(\mathcal {D})) \to \operatorname {\mathrm {Th}}_{\mathbb {P}^{k+1}}(\mathcal {O}(\mathcal {D}))$
is an isomorphism in
$\operatorname {\mathrm {Th}}_{\mathbb {P}^{k-1}}(\mathcal {O}(\mathcal {D})) \to \operatorname {\mathrm {Th}}_{\mathbb {P}^k}(\mathcal {O}(\mathcal {D})) \to \operatorname {\mathrm {Th}}_{\mathbb {P}^{k+1}}(\mathcal {O}(\mathcal {D}))$
is an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, hence
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, hence
![]() $\operatorname {\mathrm {Th}}_{\mathbb {P}^{k-1}}(\mathcal {O}(\mathcal {D})) \to \operatorname {\mathrm {Th}}_{\mathbb {P}^k}(\mathcal {O}(\mathcal {D}))$
admits a retraction, giving a splitting of the triangle (4.1.3.a). In view of equation (ii), this proves equation (iv).
$\operatorname {\mathrm {Th}}_{\mathbb {P}^{k-1}}(\mathcal {O}(\mathcal {D})) \to \operatorname {\mathrm {Th}}_{\mathbb {P}^k}(\mathcal {O}(\mathcal {D}))$
admits a retraction, giving a splitting of the triangle (4.1.3.a). In view of equation (ii), this proves equation (iv).
Corollary 4.1.4. If
![]() $k \in \mathbb {N}$
is even, the structural morphism
$k \in \mathbb {N}$
is even, the structural morphism
![]() $\mathbb {P}^k \to S$
induces an isomorphism
$\mathbb {P}^k \to S$
induces an isomorphism
![]() $\Sigma ^{\infty }_+ \mathbb {P}^k \xrightarrow {\sim } \mathbf {1}_S$
in
$\Sigma ^{\infty }_+ \mathbb {P}^k \xrightarrow {\sim } \mathbf {1}_S$
in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
Proof. The structural morphism is retraction of
![]() $\iota _k$
, so the corollary follows from (4.1.3.ii) applied with
$\iota _k$
, so the corollary follows from (4.1.3.ii) applied with
![]() $r=0$
.
$r=0$
.
Proposition 4.1.5. Let
![]() $E,V_1,\ldots ,V_n$
be vector bundles of constant rank over S, and
$E,V_1,\ldots ,V_n$
be vector bundles of constant rank over S, and
![]() $d_1,\ldots ,d_n \in \mathbb {Z}$
. Assume that
$d_1,\ldots ,d_n \in \mathbb {Z}$
. Assume that
![]() $\operatorname {\mathrm {rank}} E$
is even and that
$\operatorname {\mathrm {rank}} E$
is even and that
![]() $d_1 \operatorname {\mathrm {rank}} V_1 +\cdots +d_n \operatorname {\mathrm {rank}} V_n$
is odd. Then
$d_1 \operatorname {\mathrm {rank}} V_1 +\cdots +d_n \operatorname {\mathrm {rank}} V_n$
is odd. Then
where
![]() $q \colon \mathbb {P}(E) \to S$
is the projective bundle.
$q \colon \mathbb {P}(E) \to S$
is the projective bundle.
Proof. By (1.10) and (1.9), this may be verified Zariski locally on S, so we may assume that
![]() $E,V_1,\ldots ,V_n$
are all trivial. Then the statement follows from (4.1.3.i).
$E,V_1,\ldots ,V_n$
are all trivial. Then the statement follows from (4.1.3.i).
Proposition 4.1.6. Let
![]() $E,V$
be vector bundles over S. Assume that E has constant odd rank. Then
$E,V$
be vector bundles over S. Assume that E has constant odd rank. Then
![]() $\operatorname {\mathrm {Th}}_{\mathbb {P}(E)}(V) \to \operatorname {\mathrm {Th}}_S(V)$
is an isomorphism in
$\operatorname {\mathrm {Th}}_{\mathbb {P}(E)}(V) \to \operatorname {\mathrm {Th}}_S(V)$
is an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
. In particular,
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
. In particular,
![]() $\Sigma ^{\infty }_+ \mathbb {P}(E) \xrightarrow {\sim } \mathbf {1}_S$
in
$\Sigma ^{\infty }_+ \mathbb {P}(E) \xrightarrow {\sim } \mathbf {1}_S$
in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
4.2 Odd rank vector bundles
4.2.1
Let
![]() $E\to S$
be a vector bundle. The composite
$E\to S$
be a vector bundle. The composite
![]() $\mathcal {O}(-1) \subset E \times _S \mathbb {P}(E) \to E$
restricts to an isomorphism
$\mathcal {O}(-1) \subset E \times _S \mathbb {P}(E) \to E$
restricts to an isomorphism
![]() $\mathcal {O}(-1)^{\circ } \xrightarrow {\sim } E^\circ $
, which is
$\mathcal {O}(-1)^{\circ } \xrightarrow {\sim } E^\circ $
, which is
![]() $\mathbb {G}_m$
-equivariant. We thus obtain a commutative diagram in
$\mathbb {G}_m$
-equivariant. We thus obtain a commutative diagram in
![]() $\operatorname {\mathrm {Spt}}(S)$
$\operatorname {\mathrm {Spt}}(S)$

which induces a morphism of the homotopy cofibers of the horizontal morphisms:
Lemma 4.2.2. Let
![]() $E \to S$
be a vector bundle of constant odd rank. Then equation (4.2.1.b) is an isomorphism
$E \to S$
be a vector bundle of constant odd rank. Then equation (4.2.1.b) is an isomorphism
![]() $\operatorname {\mathrm {Th}}_{\mathbb {P}(E)}(\mathcal {O}(-1)) \xrightarrow {\sim } \operatorname {\mathrm {Th}}_S(E)$
in
$\operatorname {\mathrm {Th}}_{\mathbb {P}(E)}(\mathcal {O}(-1)) \xrightarrow {\sim } \operatorname {\mathrm {Th}}_S(E)$
in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
Proof. It follows from (4.1.6) that both vertical arrows in the diagram (4.2.1.a) are isomorphisms in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, hence so the induced map on homotopy cofibers.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, hence so the induced map on homotopy cofibers.
Proposition 4.2.3. Let
![]() $E \to S$
be a vector bundle of constant odd rank. Then the projection
$E \to S$
be a vector bundle of constant odd rank. Then the projection
![]() $E^\circ \to S$
admits a section in
$E^\circ \to S$
admits a section in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, inducing a decomposition in
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, inducing a decomposition in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
Proof. By (2.2.6), we have a splitting in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
and the statement follows from (4.2.1), (4.1.6) and (4.2.2).
Remark 4.2.4. One may deduce that (2.2.7) and (2.2.8) remain valid when L is an odd rank vector bundle instead of a line bundle, using exactly the same arguments but substituting (4.2.3) for (2.2.6).
We deduce the following splitting principle.
Corollary 4.2.5. Let
![]() $X \in \operatorname {\mathrm {Sm}}_S$
, and
$X \in \operatorname {\mathrm {Sm}}_S$
, and
![]() $E \to X$
be a vector bundle of constant odd rank. Then there exists a morphism
$E \to X$
be a vector bundle of constant odd rank. Then there exists a morphism
![]() $f\colon Y \to X$
in
$f\colon Y \to X$
in
![]() $\operatorname {\mathrm {Sm}}_S$
whose image in
$\operatorname {\mathrm {Sm}}_S$
whose image in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
admits a section, and a vector bundle
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
admits a section, and a vector bundle
![]() $F \to Y$
such that
$F \to Y$
such that
![]() $f^*E \simeq F \oplus 1$
.
$f^*E \simeq F \oplus 1$
.
Proof. Applying the functor
![]() $\operatorname {\mathrm {SH}}(X)[\eta ^{-1}] \to \operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
of (1.9) we may assume that
$\operatorname {\mathrm {SH}}(X)[\eta ^{-1}] \to \operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
of (1.9) we may assume that
![]() $X=S$
. Let us denote by
$X=S$
. Let us denote by
![]() $p\colon (E^\vee )^\circ \to S$
the projection. Then
$p\colon (E^\vee )^\circ \to S$
the projection. Then
![]() $p^*E^\vee $
admits a nowhere vanishing section s. Its dual
$p^*E^\vee $
admits a nowhere vanishing section s. Its dual
![]() $s^\vee \colon p^*E \to 1$
is surjective. Letting
$s^\vee \colon p^*E \to 1$
is surjective. Letting
![]() $Q = \ker s^\vee $
, we have an exact sequence of vector bundles over
$Q = \ker s^\vee $
, we have an exact sequence of vector bundles over
![]() $(E^\vee )^\circ $
$(E^\vee )^\circ $
Then we may find an affine bundle
![]() $g \colon Y \to (E^\vee )^\circ $
along which the pullback of the sequence (4.2.5.a) splits (we may take for Y the scheme parametrising the sections of
$g \colon Y \to (E^\vee )^\circ $
along which the pullback of the sequence (4.2.5.a) splits (we may take for Y the scheme parametrising the sections of
![]() $p^*E^\vee \to Q^\vee $
; see, e.g., [Reference RiouRio10, p.243]). Then
$p^*E^\vee \to Q^\vee $
; see, e.g., [Reference RiouRio10, p.243]). Then
![]() $\Sigma ^{\infty }_+ g \colon \Sigma ^{\infty }_+ Y \to \Sigma ^{\infty }_+ (E^\vee )^\circ $
is an isomorphism in
$\Sigma ^{\infty }_+ g \colon \Sigma ^{\infty }_+ Y \to \Sigma ^{\infty }_+ (E^\vee )^\circ $
is an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)$
, and
$\operatorname {\mathrm {SH}}(S)$
, and
![]() $\Sigma ^{\infty }_+ p\colon \Sigma ^{\infty }_+ (E^\vee )^\circ \to \mathbf {1}_S$
admits a section in
$\Sigma ^{\infty }_+ p\colon \Sigma ^{\infty }_+ (E^\vee )^\circ \to \mathbf {1}_S$
admits a section in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
by (4.2.3). So we may set
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
by (4.2.3). So we may set
![]() $f =p \circ g$
.
$f =p \circ g$
.
4.3 Thom spaces of tensor products by line bundles
We are now in position to slightly improve the result obtained in §3.3.
Lemma 4.3.1. Let
![]() $E \to S$
be a vector bundle and
$E \to S$
be a vector bundle and
![]() $u \in H^0(S,\mathbb {G}_m)$
. Assume that E has constant rank r. Then in the notation of (1.5) and (1.6), we have in
$u \in H^0(S,\mathbb {G}_m)$
. Assume that E has constant rank r. Then in the notation of (1.5) and (1.6), we have in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
Proof. Since, under the identification
![]() $\operatorname {\mathrm {Th}}_S(E\oplus 1) = \operatorname {\mathrm {Th}}_S(E) \wedge \operatorname {\mathrm {Th}}_S(1)$
(see equation (1.3.b)) we have
$\operatorname {\mathrm {Th}}_S(E\oplus 1) = \operatorname {\mathrm {Th}}_S(E) \wedge \operatorname {\mathrm {Th}}_S(1)$
(see equation (1.3.b)) we have
we may replace E with
![]() $E\oplus 1$
if necessary and thus assume that r is odd. The
$E\oplus 1$
if necessary and thus assume that r is odd. The
![]() $\mathbb {G}_m$
-equivariant isomorphism
$\mathbb {G}_m$
-equivariant isomorphism
![]() $E^\circ \simeq \mathcal {O}(-1)^\circ $
(see (4.2.1)) yields a commutative square in
$E^\circ \simeq \mathcal {O}(-1)^\circ $
(see (4.2.1)) yields a commutative square in
![]() $\operatorname {\mathrm {SH}}(S)$
$\operatorname {\mathrm {SH}}(S)$

where the vertical arrows coincide and are isomorphisms in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
by (4.2.2). In view of equation (1.6.b), we may replace
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
by (4.2.2). In view of equation (1.6.b), we may replace
![]() $E \to S$
with
$E \to S$
with
![]() $\mathcal {O}(-1) \to \mathbb {P}(E)$
, and thus assume that E is a line bundle. By (2.2.8), we may replace S with
$\mathcal {O}(-1) \to \mathbb {P}(E)$
, and thus assume that E is a line bundle. By (2.2.8), we may replace S with
![]() $E^\circ $
, and thus assume that the line bundle
$E^\circ $
, and thus assume that the line bundle
![]() $E \to S$
admits a trivialisation
$E \to S$
admits a trivialisation
![]() $\alpha \colon 1 \xrightarrow {\sim } E$
. Then we have a commutative square of isomorphisms in
$\alpha \colon 1 \xrightarrow {\sim } E$
. Then we have a commutative square of isomorphisms in
![]() $\operatorname {\mathrm {SH}}(S)$
$\operatorname {\mathrm {SH}}(S)$

By definition
![]() $\operatorname {\mathrm {Th}}(u \operatorname {\mathrm {id}}_1) = \langle u \rangle $
, and we deduce using equation (1.6.b) that
$\operatorname {\mathrm {Th}}(u \operatorname {\mathrm {id}}_1) = \langle u \rangle $
, and we deduce using equation (1.6.b) that
![]() $\operatorname {\mathrm {Th}}(u \operatorname {\mathrm {id}}_E) = \langle u \rangle \in \operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {SH}}(S)}(\operatorname {\mathrm {Th}}_S(E))$
. Since
$\operatorname {\mathrm {Th}}(u \operatorname {\mathrm {id}}_E) = \langle u \rangle \in \operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {SH}}(S)}(\operatorname {\mathrm {Th}}_S(E))$
. Since
![]() $\langle u^2 \rangle =\operatorname {\mathrm {id}}$
by (2.1.1) and r is odd, it follows that
$\langle u^2 \rangle =\operatorname {\mathrm {id}}$
by (2.1.1) and r is odd, it follows that
![]() $\langle u \rangle = \langle u^r \rangle $
, concluding the proof.
$\langle u \rangle = \langle u^r \rangle $
, concluding the proof.
Proposition 4.3.2. Let
![]() $L \to S$
be a line bundle, and
$L \to S$
be a line bundle, and
![]() $V \to S$
a vector bundle of constant rank r. If
$V \to S$
a vector bundle of constant rank r. If
![]() $s \in \mathbb {Z}$
is such that
$s \in \mathbb {Z}$
is such that
![]() $rs$
is even, then there exists an isomorphism in
$rs$
is even, then there exists an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
Proof. Upon replacing V with
![]() $V \otimes L^{\otimes s}$
, we may assume that
$V \otimes L^{\otimes s}$
, we may assume that
![]() $s \geq 0$
. When
$s \geq 0$
. When
![]() $\alpha \colon 1 \xrightarrow {\sim }L$
is a trivialisation of the line bundle L over S we have an isomorphism in
$\alpha \colon 1 \xrightarrow {\sim }L$
is a trivialisation of the line bundle L over S we have an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)$
$\operatorname {\mathrm {SH}}(S)$
Any trivialisation of L is of the form
![]() $u \alpha $
for some
$u \alpha $
for some
![]() $u \in H^0(S,\mathbb {G}_m)$
, and we have in
$u \in H^0(S,\mathbb {G}_m)$
, and we have in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, by (4.3.1) and (2.1.1)
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, by (4.3.1) and (2.1.1)
It follows that the image of the isomorphism (4.3.2.a) in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
is independent of the choice of the trivialisation
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
is independent of the choice of the trivialisation
![]() $\alpha $
, and we conclude as in the proof of (3.3.1).
$\alpha $
, and we conclude as in the proof of (3.3.1).
5 Classifying spaces and characters
5.1 Models for étale classifying spaces
Here, we recall some facts concerning the geometric models of the étale classifying space of a linear algebraic group given in [Reference Morel and VoevodskyMV99, §4.2].
5.1.1
Let G be a linear algebraic group over S. Let
![]() $(V_m,U_m,f_m)$
, for
$(V_m,U_m,f_m)$
, for
![]() $m\in \mathbb {N} \smallsetminus \{0\}$
, be an admissible gadget with a nice (right) G-action, in the sense of [Reference Morel and VoevodskyMV99, Definition 4.2.1]. Here,
$m\in \mathbb {N} \smallsetminus \{0\}$
, be an admissible gadget with a nice (right) G-action, in the sense of [Reference Morel and VoevodskyMV99, Definition 4.2.1]. Here,
![]() $V_m \to S$
are G-equivariant vector bundles, and
$V_m \to S$
are G-equivariant vector bundles, and
![]() $U_m \subset V_m$
are G-invariant open subschemes where the G-action is free. Set
$U_m \subset V_m$
are G-invariant open subschemes where the G-action is free. Set
![]() $E_mG=U_m$
and
$E_mG=U_m$
and
![]() $B_mG = (E_mG)/G$
. Let us define
$B_mG = (E_mG)/G$
. Let us define
![]() $\mathrm {B} G \in \operatorname {\mathrm {Spc}}(S)$
as the colimit of the motivic spaces
$\mathrm {B} G \in \operatorname {\mathrm {Spc}}(S)$
as the colimit of the motivic spaces
![]() $B_m G$
as m runs over
$B_m G$
as m runs over
![]() $\mathbb {N} \smallsetminus \{0\}$
. It is proved in [Reference Morel and VoevodskyMV99, Proposition 4.2.6] that the weak-equivalence class of
$\mathbb {N} \smallsetminus \{0\}$
. It is proved in [Reference Morel and VoevodskyMV99, Proposition 4.2.6] that the weak-equivalence class of
![]() $\mathrm {B} G$
does not depend on the choice of
$\mathrm {B} G$
does not depend on the choice of
![]() $(V_m,U_m,f_m)$
. More precisely if
$(V_m,U_m,f_m)$
. More precisely if
![]() $(V_m,U_m,f_m),(V^{\prime }_m,U^{\prime }_m,f^{\prime }_m)$
are admissible gadgets with a nice G-action, and
$(V_m,U_m,f_m),(V^{\prime }_m,U^{\prime }_m,f^{\prime }_m)$
are admissible gadgets with a nice G-action, and
![]() $U_m \to U^{\prime }_m$
are G-equivariant morphisms commuting with the morphisms
$U_m \to U^{\prime }_m$
are G-equivariant morphisms commuting with the morphisms
![]() $f_m,f_m'$
, then the induced morphism of motivic spaces
$f_m,f_m'$
, then the induced morphism of motivic spaces
![]() $\operatorname {\mathrm {colim}}_m (U_m/G) \to \operatorname {\mathrm {colim}}_m (U^{\prime }_m/G)$
is a weak equivalence. In the sequel, we will refer to a system
$\operatorname {\mathrm {colim}}_m (U_m/G) \to \operatorname {\mathrm {colim}}_m (U^{\prime }_m/G)$
is a weak equivalence. In the sequel, we will refer to a system
![]() $(V_m,U_m,f_m)$
as above as a model for
$(V_m,U_m,f_m)$
as above as a model for
![]() $\mathrm {B} G$
and use the notation
$\mathrm {B} G$
and use the notation
![]() $E_mG,B_mG$
.
$E_mG,B_mG$
.
5.1.2
In the situation of (5.1.1), since
![]() $B_1G$
is cofibrant and each
$B_1G$
is cofibrant and each
![]() $B_m G \to B_{m+1} G$
is a cofibration (for the model structure of [Reference Morel and VoevodskyMV99]), it follows that the colimit
$B_m G \to B_{m+1} G$
is a cofibration (for the model structure of [Reference Morel and VoevodskyMV99]), it follows that the colimit
![]() $\mathrm {B} G$
is canonically weakly equivalent to the homotopy colimit of the motivic spaces
$\mathrm {B} G$
is canonically weakly equivalent to the homotopy colimit of the motivic spaces
![]() $B_mG$
in
$B_mG$
in
![]() $\operatorname {\mathrm {Spc}}(S)$
(see, e.g., [Reference HirschhornHir03, Theorem 19.9.1]).
$\operatorname {\mathrm {Spc}}(S)$
(see, e.g., [Reference HirschhornHir03, Theorem 19.9.1]).
5.1.3
Let G be a linear algebraic group over S, and choose a model for
![]() $\mathrm {B} G$
. Since the map
$\mathrm {B} G$
. Since the map
![]() $\operatorname {\mathrm {colim}}_m E_mG \to S$
is a weak equivalence of motivic spaces [Reference Morel and VoevodskyMV99, Proposition 4.2.3], we obtain a canonical morphism
$\operatorname {\mathrm {colim}}_m E_mG \to S$
is a weak equivalence of motivic spaces [Reference Morel and VoevodskyMV99, Proposition 4.2.3], we obtain a canonical morphism
![]() $S \to \mathrm {B} G$
in
$S \to \mathrm {B} G$
in
![]() $\operatorname {\mathrm {H}}(S)$
. We say that the model is pointed if we are given an S-point of
$\operatorname {\mathrm {H}}(S)$
. We say that the model is pointed if we are given an S-point of
![]() $E_1 G$
. This yields map
$E_1 G$
. This yields map
![]() $S \to \mathrm {B} G$
in
$S \to \mathrm {B} G$
in
![]() $\operatorname {\mathrm {Spc}}(S)$
, whose image in
$\operatorname {\mathrm {Spc}}(S)$
, whose image in
![]() $\operatorname {\mathrm {H}}(S)$
is the canonical morphism described just above.
$\operatorname {\mathrm {H}}(S)$
is the canonical morphism described just above.
5.1.4
(See also [Reference Morel and VoevodskyMV99, p.133].) Let us fix an integer
![]() $n\in \mathbb {N}$
and describe an explicit model for
$n\in \mathbb {N}$
and describe an explicit model for
![]() $\operatorname {\mathrm {BGL}}_n$
. Fix an integer
$\operatorname {\mathrm {BGL}}_n$
. Fix an integer
![]() $p \geq n$
(we will typically take
$p \geq n$
(we will typically take
![]() $p=n$
). For
$p=n$
). For
![]() $s \in \mathbb {N}$
, we denote by
$s \in \mathbb {N}$
, we denote by
![]() $\operatorname {\mathrm {Gr}}(n,s)$
the Grassmannian of rank n subbundles
$\operatorname {\mathrm {Gr}}(n,s)$
the Grassmannian of rank n subbundles
![]() $U\subset 1^{\oplus s}$
over S (for us a subbundle is locally split, so
$U\subset 1^{\oplus s}$
over S (for us a subbundle is locally split, so
![]() $1^{\oplus s}/U$
is a vector bundle). For each
$1^{\oplus s}/U$
is a vector bundle). For each
![]() $m\in \mathbb {N} \smallsetminus \{0\}$
, consider the S-scheme
$m\in \mathbb {N} \smallsetminus \{0\}$
, consider the S-scheme
![]() $V_{m,p}$
parametrising the vector bundles maps
$V_{m,p}$
parametrising the vector bundles maps
![]() $1^{\oplus n} \to 1^{\oplus pm}$
; then
$1^{\oplus n} \to 1^{\oplus pm}$
; then
![]() $V_{m,p} \to S$
is a vector bundle. Let
$V_{m,p} \to S$
is a vector bundle. Let
![]() $U_{m,p}$
the open subscheme of
$U_{m,p}$
the open subscheme of
![]() $V_{m,p}$
parametrising those vector bundle maps admitting Zariski locally a retraction (i.e., making
$V_{m,p}$
parametrising those vector bundle maps admitting Zariski locally a retraction (i.e., making
![]() $1^{\oplus n}$
a subbundle of
$1^{\oplus n}$
a subbundle of
![]() $1^{\oplus pm}$
). Then the natural left
$1^{\oplus pm}$
). Then the natural left
![]() $\operatorname {\mathrm {GL}}_n$
-action on
$\operatorname {\mathrm {GL}}_n$
-action on
![]() $1^{\oplus n}$
induces a right
$1^{\oplus n}$
induces a right
![]() $\operatorname {\mathrm {GL}}_n$
-action on
$\operatorname {\mathrm {GL}}_n$
-action on
![]() $U_{m,p}$
, which is free, and the quotient
$U_{m,p}$
, which is free, and the quotient
![]() $U_{m,p}/\operatorname {\mathrm {GL}}_n$
can be identified with the Grassmannian
$U_{m,p}/\operatorname {\mathrm {GL}}_n$
can be identified with the Grassmannian
![]() $\operatorname {\mathrm {Gr}}(n,pm)$
. The inclusion
$\operatorname {\mathrm {Gr}}(n,pm)$
. The inclusion
![]() $1^{\oplus m} \subset 1^{\oplus m+1}$
given by the vanishing of the last coordinate induces an inclusion
$1^{\oplus m} \subset 1^{\oplus m+1}$
given by the vanishing of the last coordinate induces an inclusion
which yields a
![]() $\operatorname {\mathrm {GL}}_n$
-equivariant morphism
$\operatorname {\mathrm {GL}}_n$
-equivariant morphism
![]() $f_{m,p} \colon U_{m,p} \to U_{m+1,p}$
.
$f_{m,p} \colon U_{m,p} \to U_{m+1,p}$
.
Then the family
![]() $(V_{m,p},U_{m,p},f_{m,p})$
is an admissible gadget with a nice
$(V_{m,p},U_{m,p},f_{m,p})$
is an admissible gadget with a nice
![]() $\operatorname {\mathrm {GL}}_n$
-action. Indeed, the first condition of [Reference Morel and VoevodskyMV99, Definition 4.2.1] is satisfied because
$\operatorname {\mathrm {GL}}_n$
-action. Indeed, the first condition of [Reference Morel and VoevodskyMV99, Definition 4.2.1] is satisfied because
![]() $U_{1,p}$
possesses an S-point, and the second condition is satisfied with
$U_{1,p}$
possesses an S-point, and the second condition is satisfied with
![]() $j=2i$
. The fact that the group
$j=2i$
. The fact that the group
![]() $\operatorname {\mathrm {GL}}_n$
is special implies the validity of condition (3) of [Reference Morel and VoevodskyMV99, Definition 4.2.4]. We thus obtained a model for
$\operatorname {\mathrm {GL}}_n$
is special implies the validity of condition (3) of [Reference Morel and VoevodskyMV99, Definition 4.2.4]. We thus obtained a model for
![]() $\operatorname {\mathrm {BGL}}_n$
. We have just seen that this model is pointed (in the sense of (5.1.3)); a canonical pointing when
$\operatorname {\mathrm {BGL}}_n$
. We have just seen that this model is pointed (in the sense of (5.1.3)); a canonical pointing when
![]() $p=n$
is induced by the identity of
$p=n$
is induced by the identity of
![]() $1^{\oplus n}$
.
$1^{\oplus n}$
.
5.1.5
Let
![]() $H \subset G$
be an inclusion of linear algebraic groups over S. Then any admissible gadget with a nice G-action is also one with a nice H-action (where the H-action is given by restricting the G-action). Indeed, the only nonimmediate point is condition (3) of [Reference Morel and VoevodskyMV99, Definition 4.2.4]. So let F be a smooth S-scheme with a free right H-action. Consider the quotient
$H \subset G$
be an inclusion of linear algebraic groups over S. Then any admissible gadget with a nice G-action is also one with a nice H-action (where the H-action is given by restricting the G-action). Indeed, the only nonimmediate point is condition (3) of [Reference Morel and VoevodskyMV99, Definition 4.2.4]. So let F be a smooth S-scheme with a free right H-action. Consider the quotient
![]() $E=(F \times G)/H$
, where the right H-action on G is given by letting
$E=(F \times G)/H$
, where the right H-action on G is given by letting
![]() $h \in H$
act via
$h \in H$
act via
![]() $g \mapsto h^{-1}g$
. Right multiplication in G induces a free right G-action on E. For any
$g \mapsto h^{-1}g$
. Right multiplication in G induces a free right G-action on E. For any
![]() $U \in \operatorname {\mathrm {Sm}}_S$
with a right G-action, we have isomorphisms
$U \in \operatorname {\mathrm {Sm}}_S$
with a right G-action, we have isomorphisms
which are functorial in U and thus permit to identify the morphisms
![]() $(E \times U)/G \to E/G$
and
$(E \times U)/G \to E/G$
and
![]() $(F \times U)/H \to F/H$
. Since the former is an epimorphism in the Nisnevich topology (as the group G is nice), so is the latter.
$(F \times U)/H \to F/H$
. Since the former is an epimorphism in the Nisnevich topology (as the group G is nice), so is the latter.
Thus, given a model for
![]() $\mathrm {B} G$
, we obtain a model for
$\mathrm {B} G$
, we obtain a model for
![]() $\mathrm {B} H$
, where
$\mathrm {B} H$
, where
![]() $E_mH=E_mG$
with the induced H-action. This yields morphisms
$E_mH=E_mG$
with the induced H-action. This yields morphisms
which are compatible with the transition maps as m varies and thus a map
![]() $\mathrm {B} H \to \mathrm {B} G$
.
$\mathrm {B} H \to \mathrm {B} G$
.
5.1.6
(See also [Reference Morel and VoevodskyMV99, Remark 4.2.7].) Assume that G is a linear algebraic group over S, and fix an embedding
![]() $G \subset \operatorname {\mathrm {GL}}_n$
as a closed subgroup. By (5.1.5), every (pointed) model for
$G \subset \operatorname {\mathrm {GL}}_n$
as a closed subgroup. By (5.1.5), every (pointed) model for
![]() $\operatorname {\mathrm {BGL}}_n$
induces a (pointed) model for
$\operatorname {\mathrm {BGL}}_n$
induces a (pointed) model for
![]() $\mathrm {B} G$
. Since
$\mathrm {B} G$
. Since
![]() $\operatorname {\mathrm {BGL}}_n$
admits a pointed model by (5.1.4), so does
$\operatorname {\mathrm {BGL}}_n$
admits a pointed model by (5.1.4), so does
![]() $\mathrm {B} G$
.
$\mathrm {B} G$
.
5.2 Products
5.2.1
Let
![]() $G,G'$
be linear algebraic groups over S. Choose admissible gadgets
$G,G'$
be linear algebraic groups over S. Choose admissible gadgets
![]() $(V_m,U_m,f_m)$
with a nice G-action, and
$(V_m,U_m,f_m)$
with a nice G-action, and
![]() $(V^{\prime }_m,U^{\prime }_m,f^{\prime }_m)$
with a nice
$(V^{\prime }_m,U^{\prime }_m,f^{\prime }_m)$
with a nice
![]() $G'$
-action (in the sense of [Reference Morel and VoevodskyMV99, Definition 4.2.1], recall from (5.1.6) that such exist). Then the family
$G'$
-action (in the sense of [Reference Morel and VoevodskyMV99, Definition 4.2.1], recall from (5.1.6) that such exist). Then the family
![]() $(V_m \times V_m',U_m \times U_m',f_m \times f_m')$
constitutes an admissible gadget with a nice
$(V_m \times V_m',U_m \times U_m',f_m \times f_m')$
constitutes an admissible gadget with a nice
![]() $G \times G'$
-action. Indeed, to check the last condition of [Reference Morel and VoevodskyMV99, Definition 4.2.4], let
$G \times G'$
-action. Indeed, to check the last condition of [Reference Morel and VoevodskyMV99, Definition 4.2.4], let
![]() $T \to X$
be a
$T \to X$
be a
![]() $G\times G'$
-torsor in
$G\times G'$
-torsor in
![]() $\operatorname {\mathrm {Sm}}_S$
. Then the projection
$\operatorname {\mathrm {Sm}}_S$
. Then the projection
![]() $(T \times U \times U')/(G\times G') \to T/(G\times G')$
factors as
$(T \times U \times U')/(G\times G') \to T/(G\times G')$
factors as
where
![]() $T_1 = (T \times U)/G$
followed by
$T_1 = (T \times U)/G$
followed by
where
![]() $T_2 = T/G'$
. Each morphism is an epimorphism in the Nisnevich topology by assumption, hence so is their composite.
$T_2 = T/G'$
. Each morphism is an epimorphism in the Nisnevich topology by assumption, hence so is their composite.
Under this choice of a model for
![]() $\mathrm {B} G$
, we have
$\mathrm {B} G$
, we have
Lemma 5.2.2. If
![]() $G,G'$
are linear algebraic groups over S, we have an isomorphism
$G,G'$
are linear algebraic groups over S, we have an isomorphism
Proof. Since the product with a given motivic space commutes with homotopy colimits, we have isomorphisms in
![]() $\operatorname {\mathrm {H}}(S)$
$\operatorname {\mathrm {H}}(S)$
 $$ \begin{align*} \mathrm{B} (G \times G')&\simeq \operatorname{\mathrm{hocolim}}_m (B_mG \times B_mG') && \text{by equation (5.2.1.a) and (5.1.2)}\\ &\simeq \operatorname{\mathrm{hocolim}}_m \operatorname{\mathrm{hocolim}}_d (B_mG \times B_dG') && \text{by a cofinality argument}\\ &\simeq \operatorname{\mathrm{hocolim}}_m (B_mG \times \operatorname{\mathrm{hocolim}}_d B_dG') \\ &\simeq (\operatorname{\mathrm{hocolim}}_m B_mG) \times (\operatorname{\mathrm{hocolim}}_d B_dG')\\ &\simeq \mathrm{B} G \times \mathrm{B} G'&&\text{by (5.1.2).}\\[-35pt]\end{align*} $$
$$ \begin{align*} \mathrm{B} (G \times G')&\simeq \operatorname{\mathrm{hocolim}}_m (B_mG \times B_mG') && \text{by equation (5.2.1.a) and (5.1.2)}\\ &\simeq \operatorname{\mathrm{hocolim}}_m \operatorname{\mathrm{hocolim}}_d (B_mG \times B_dG') && \text{by a cofinality argument}\\ &\simeq \operatorname{\mathrm{hocolim}}_m (B_mG \times \operatorname{\mathrm{hocolim}}_d B_dG') \\ &\simeq (\operatorname{\mathrm{hocolim}}_m B_mG) \times (\operatorname{\mathrm{hocolim}}_d B_dG')\\ &\simeq \mathrm{B} G \times \mathrm{B} G'&&\text{by (5.1.2).}\\[-35pt]\end{align*} $$
5.3 Characters
In this section, we discuss general facts relating the classifying space of a linear algebraic group G to that of the kernel H of a character of G, which will be applied to explicit situations in §6.
5.3.1
Let G be a linear algebraic group over S, and fix a model for
![]() $\mathrm {B} G$
(see (5.1.1)). Assume given a character of G, that is a morphism of algebraic groups
$\mathrm {B} G$
(see (5.1.1)). Assume given a character of G, that is a morphism of algebraic groups
![]() $\chi \colon G \to \mathbb {G}_m$
. Considering the right G-action on
$\chi \colon G \to \mathbb {G}_m$
. Considering the right G-action on
![]() ${\mathbb {A}}^1$
given by letting
${\mathbb {A}}^1$
given by letting
![]() $g\in G$
act via
$g\in G$
act via
![]() $\lambda \mapsto \chi (g)^{-1} \lambda $
, we define for each
$\lambda \mapsto \chi (g)^{-1} \lambda $
, we define for each
![]() $m \in \mathbb {N} \smallsetminus \{0\}$
a line bundle over
$m \in \mathbb {N} \smallsetminus \{0\}$
a line bundle over
![]() $B_mG$
:
$B_mG$
:
The assignment
![]() $\chi \mapsto C_m(\chi )$
satisfies
$\chi \mapsto C_m(\chi )$
satisfies
yielding group morphisms
Let now
![]() $H \subset G$
be a closed subgroup, and consider the morphisms
$H \subset G$
be a closed subgroup, and consider the morphisms
![]() $B_m H \to B_mG$
defined in (5.1.5). If
$B_m H \to B_mG$
defined in (5.1.5). If
![]() $\chi |_H$
denotes the restriction of the character
$\chi |_H$
denotes the restriction of the character
![]() $\chi $
to H, then
$\chi $
to H, then
If
![]() $G'$
is a linear algebraic group over S, letting
$G'$
is a linear algebraic group over S, letting
![]() $\tilde {\chi }\colon G \times G' \to G \xrightarrow {\chi } \mathbb {G}_m$
be the induced character of
$\tilde {\chi }\colon G \times G' \to G \xrightarrow {\chi } \mathbb {G}_m$
be the induced character of
![]() $G \times G'$
, we have
$G \times G'$
, we have
5.3.2
Let G be a linear algebraic group over S and
![]() $\chi $
a surjective character of G. Letting
$\chi $
a surjective character of G. Letting
![]() $H=\ker \chi $
, we thus have an exact sequence of algebraic groups over S
$H=\ker \chi $
, we thus have an exact sequence of algebraic groups over S
Let us fix a model for
![]() $\mathrm {B} G$
. As explained in (5.1.5), this yields a model for
$\mathrm {B} G$
. As explained in (5.1.5), this yields a model for
![]() $\mathrm {B} H$
, and morphisms
$\mathrm {B} H$
, and morphisms
![]() $p_m \colon B_mH \to B_mG$
for
$p_m \colon B_mH \to B_mG$
for
![]() $m \in \mathbb {N} \smallsetminus \{0\}$
. By (5.3.1), we also have a line bundle
$m \in \mathbb {N} \smallsetminus \{0\}$
. By (5.3.1), we also have a line bundle
![]() $C_m(\chi )$
over
$C_m(\chi )$
over
![]() $B_mG$
such that
$B_mG$
such that
In view of (1.3.a), this yields a cofiber sequence in
![]() ${\mathrm{Spc}_{\bullet }}(S)$
, for each
${\mathrm{Spc}_{\bullet }}(S)$
, for each
![]() $m\in \mathbb {N}\smallsetminus \{0\}$
$m\in \mathbb {N}\smallsetminus \{0\}$
More generally (as in (1.4)), if
![]() $V \to B_mG$
is a vector bundle, we have a cofiber sequence in
$V \to B_mG$
is a vector bundle, we have a cofiber sequence in
![]() ${\mathrm{Spc}_{\bullet }}(S)$
,
${\mathrm{Spc}_{\bullet }}(S)$
,
5.3.3
In the situation of (5.3.2), let us define
As in (5.1.2), this coincides with the homotopy colimit (the transition morphisms are again monomorphisms, being directed colimits of such). We will also write
![]() $\operatorname {\mathrm {Th}}_{\mathrm {B} G}(C(\chi )) \in \operatorname {\mathrm {Spt}}(S)$
instead of
$\operatorname {\mathrm {Th}}_{\mathrm {B} G}(C(\chi )) \in \operatorname {\mathrm {Spt}}(S)$
instead of
![]() $\Sigma ^{\infty } \operatorname {\mathrm {Th}}_{\mathrm {B} G}(C(\chi ))$
. Taking the (homotopy) colimit of equation (5.3.2.b) yields a cofiber sequence in
$\Sigma ^{\infty } \operatorname {\mathrm {Th}}_{\mathrm {B} G}(C(\chi ))$
. Taking the (homotopy) colimit of equation (5.3.2.b) yields a cofiber sequence in
![]() ${\mathrm{Spc}_{\bullet }}(S)$
${\mathrm{Spc}_{\bullet }}(S)$
5.3.4
In the situation of (5.3.2), assume that the model for
![]() $\mathrm {B} G$
is pointed. Then we have a commutative diagram of S-schemes with Cartesian squares
$\mathrm {B} G$
is pointed. Then we have a commutative diagram of S-schemes with Cartesian squares

where
![]() $e_1$
is induced by the S-point and the G-action on
$e_1$
is induced by the S-point and the G-action on
![]() $E_1G$
, and
$E_1G$
, and
![]() $j_1$
, resp.
$j_1$
, resp.
![]() $i_1$
, is obtained by taking the H-quotient, resp. G-quotient of
$i_1$
, is obtained by taking the H-quotient, resp. G-quotient of
![]() $e_1$
. Composing
$e_1$
. Composing
![]() $i_1$
and
$i_1$
and
![]() $j_1$
with the natural maps
$j_1$
with the natural maps
![]() $B_1 G \to \mathrm {B} G$
and
$B_1 G \to \mathrm {B} G$
and
![]() $B_1 H \to \mathrm {B} H$
respectively, we obtain maps
$B_1 H \to \mathrm {B} H$
respectively, we obtain maps
![]() $i \colon S \to \mathrm {B} G$
and
$i \colon S \to \mathrm {B} G$
and
![]() $j \colon \mathbb {G}_m \to \mathrm {B} H$
in
$j \colon \mathbb {G}_m \to \mathrm {B} H$
in
![]() $\operatorname {\mathrm {Spc}}(S)$
. Note that i is the map described in (5.1.3) and that the left-hand Cartesian square in equation (5.3.4.a) shows that the map
$\operatorname {\mathrm {Spc}}(S)$
. Note that i is the map described in (5.1.3) and that the left-hand Cartesian square in equation (5.3.4.a) shows that the map
![]() $j \colon \mathbb {G}_m \to \mathrm {B} H$
classifies the H-torsor
$j \colon \mathbb {G}_m \to \mathrm {B} H$
classifies the H-torsor
![]() $\chi \colon G \to \mathbb {G}_m$
.
$\chi \colon G \to \mathbb {G}_m$
.
The right-hand Cartesian square in equation (5.3.4.a) shows that the
![]() $\mathbb {G}_m$
-torsor
$\mathbb {G}_m$
-torsor
![]() $B_1 H \to B_1G$
pulls back to the trivial torsor along
$B_1 H \to B_1G$
pulls back to the trivial torsor along
![]() $i_1$
, which yields a trivialisation of the line bundle
$i_1$
, which yields a trivialisation of the line bundle
![]() $i_1^*C_1(\chi )$
over S and thus a morphism in
$i_1^*C_1(\chi )$
over S and thus a morphism in
![]() ${\mathrm{Spc}_{\bullet }}(S)$
${\mathrm{Spc}_{\bullet }}(S)$
We thus obtain a commutative diagram in
![]() ${\mathrm{Spc}_{\bullet }}(S)$
, whose rows are cofiber sequences
${\mathrm{Spc}_{\bullet }}(S)$
, whose rows are cofiber sequences

5.3.5
In the situation of (5.3.2), using (2.2.5) for the line bundle
![]() $C_m(\chi ) \to B_mG$
, and applying the functor
$C_m(\chi ) \to B_mG$
, and applying the functor
![]() ${\mathrm{Spc}_{\bullet }}(B_mG)[\eta ^{-1}] \to {\mathrm{Spc}_{\bullet }}(S)[\eta ^{-1}]$
of (1.9), we have homotopy cocartesian squares in
${\mathrm{Spc}_{\bullet }}(B_mG)[\eta ^{-1}] \to {\mathrm{Spc}_{\bullet }}(S)[\eta ^{-1}]$
of (1.9), we have homotopy cocartesian squares in
![]() ${\mathrm{Spc}_{\bullet }}(S)[\eta ^{-1}]$
${\mathrm{Spc}_{\bullet }}(S)[\eta ^{-1}]$

which are compatible with the transition maps as m varies by (2.2.3). Taking the homotopy colimit, and proceeding as in the proof of (2.2.6), we obtain an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
6 Computations of classifying spaces
6.1 Diagonalisable groups
Using the embeddings
![]() $\mathbb {P}^k \subset \mathbb {P}^{k+1}$
of (4.1.1) for
$\mathbb {P}^k \subset \mathbb {P}^{k+1}$
of (4.1.1) for
![]() $k \in \mathbb {N}$
, we define, for
$k \in \mathbb {N}$
, we define, for
![]() $n \in \mathbb {Z}$
$n \in \mathbb {Z}$
and as usual write
![]() $\operatorname {\mathrm {Th}}_{\mathbb {P}^\infty }(\mathcal {O}(n)) \in \operatorname {\mathrm {Spt}}(S)$
instead of
$\operatorname {\mathrm {Th}}_{\mathbb {P}^\infty }(\mathcal {O}(n)) \in \operatorname {\mathrm {Spt}}(S)$
instead of
![]() $\Sigma ^{\infty } \operatorname {\mathrm {Th}}_{\mathbb {P}^\infty }(\mathcal {O}(n))$
. We have a natural map
$\Sigma ^{\infty } \operatorname {\mathrm {Th}}_{\mathbb {P}^\infty }(\mathcal {O}(n))$
. We have a natural map
![]() $\iota _\infty \colon S=\mathbb {P}^0 \to \mathbb {P}^\infty $
in
$\iota _\infty \colon S=\mathbb {P}^0 \to \mathbb {P}^\infty $
in
![]() $\operatorname {\mathrm {Spc}}(S)$
. For each
$\operatorname {\mathrm {Spc}}(S)$
. For each
![]() $n \in \mathbb {Z}$
, the line bundle
$n \in \mathbb {Z}$
, the line bundle
![]() $\mathcal {O}(n)$
over
$\mathcal {O}(n)$
over
![]() $\mathbb {P}^0$
admits a canonical trivialisation so that equation (4.1.2.a) yields a canonical map in
$\mathbb {P}^0$
admits a canonical trivialisation so that equation (4.1.2.a) yields a canonical map in
![]() $\operatorname {\mathrm {Spt}}(S)$
$\operatorname {\mathrm {Spt}}(S)$
Proposition 6.1.1. Let
![]() $n\in \mathbb {Z}$
. The following hold in
$n\in \mathbb {Z}$
. The following hold in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
:
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
:
-
(i) The morphism
 $\iota _\infty $
induces an isomorphism
$\iota _\infty $
induces an isomorphism
 $\mathbf {1}_S \simeq \Sigma ^{\infty }_+\mathbb {P}^\infty $
.
$\mathbf {1}_S \simeq \Sigma ^{\infty }_+\mathbb {P}^\infty $
. -
(ii) If n is odd, then
 $\operatorname {\mathrm {Th}}_{\mathbb {P}^\infty }(\mathcal {O}(n)) = 0$
.
$\operatorname {\mathrm {Th}}_{\mathbb {P}^\infty }(\mathcal {O}(n)) = 0$
. -
(iii) If n is even, then equation (6.1.0.a) induces an isomorphism
 $\Sigma ^{2,1}\mathbf {1}_S \simeq \operatorname {\mathrm {Th}}_{\mathbb {P}^\infty }(\mathcal {O}(n))$
.
$\Sigma ^{2,1}\mathbf {1}_S \simeq \operatorname {\mathrm {Th}}_{\mathbb {P}^\infty }(\mathcal {O}(n))$
.
Proof. We apply (4.1.3) with
![]() $\mathcal {D} = (n)$
, and so
$\mathcal {D} = (n)$
, and so
![]() $\mathcal {O}(\mathcal {D})=\mathcal {O}(n)$
. We obtain that
$\mathcal {O}(\mathcal {D})=\mathcal {O}(n)$
. We obtain that
![]() $\Sigma ^{2,1}\mathbf {1}_S \to \operatorname {\mathrm {Th}}_{\mathbb {P}^k}(\mathcal {O}(n))$
is a weak equivalence in
$\Sigma ^{2,1}\mathbf {1}_S \to \operatorname {\mathrm {Th}}_{\mathbb {P}^k}(\mathcal {O}(n))$
is a weak equivalence in
![]() $\operatorname {\mathrm {Spt}}(S)[\eta ^{-1}]$
when
$\operatorname {\mathrm {Spt}}(S)[\eta ^{-1}]$
when
![]() $n,k$
are even. Taking the homotopy colimit over k yields a weak equivalence
$n,k$
are even. Taking the homotopy colimit over k yields a weak equivalence
![]() $\Sigma ^{2,1}\mathbf {1}_S \to \operatorname {\mathrm {Th}}_{\mathbb {P}^\infty }(\mathcal {O}(n))$
in
$\Sigma ^{2,1}\mathbf {1}_S \to \operatorname {\mathrm {Th}}_{\mathbb {P}^\infty }(\mathcal {O}(n))$
in
![]() $\operatorname {\mathrm {Spt}}(S)[\eta ^{-1}]$
when n is even. This proves equation (iii). The other statements are deduced in a similar way from (4.1.3).
$\operatorname {\mathrm {Spt}}(S)[\eta ^{-1}]$
when n is even. This proves equation (iii). The other statements are deduced in a similar way from (4.1.3).
6.1.2
Consider the model for
![]() $\mathrm {B} \mathbb {G}_m$
described in (5.1.4) with
$\mathrm {B} \mathbb {G}_m$
described in (5.1.4) with
![]() $p=n=1$
, under the identification
$p=n=1$
, under the identification
![]() $\mathbb {G}_m = \operatorname {\mathrm {GL}}_1$
. Then
$\mathbb {G}_m = \operatorname {\mathrm {GL}}_1$
. Then
![]() $B_m\mathbb {G}_m = \mathbb {P}^{m-1}$
, and thus
$B_m\mathbb {G}_m = \mathbb {P}^{m-1}$
, and thus
![]() $\mathrm {B} \mathbb {G}_m = \mathbb {P}^{\infty }$
. Furthermore, the line bundle
$\mathrm {B} \mathbb {G}_m = \mathbb {P}^{\infty }$
. Furthermore, the line bundle
![]() $C_m(\operatorname {\mathrm {id}}_{\mathbb {G}_m})$
over
$C_m(\operatorname {\mathrm {id}}_{\mathbb {G}_m})$
over
![]() $B_mG$
defined in equation (5.3.1.a) may be identified with the tautological bundle
$B_mG$
defined in equation (5.3.1.a) may be identified with the tautological bundle
![]() $\mathcal {O}(-1)$
over
$\mathcal {O}(-1)$
over
![]() $\mathbb {P}^{m-1}$
.
$\mathbb {P}^{m-1}$
.
Theorem 6.1.3. Let
![]() $n\in \mathbb {N} \smallsetminus \{0\}$
. The following hold in
$n\in \mathbb {N} \smallsetminus \{0\}$
. The following hold in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
:
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
:
-
(i) The natural morphism
 $\mathbf {1}_S \to \Sigma ^{\infty }_+\mathrm {B}\mathbb {G}_m$
is an isomorphism.
$\mathbf {1}_S \to \Sigma ^{\infty }_+\mathrm {B}\mathbb {G}_m$
is an isomorphism. -
(ii) If n is odd, the natural morphism
 $\mathbf {1}_S \to \Sigma ^{\infty }_+\mathrm {B}\mu _n$
is an isomorphism.
$\mathbf {1}_S \to \Sigma ^{\infty }_+\mathrm {B}\mu _n$
is an isomorphism. -
(iii) If n is even, the morphism
 $\mathbb {G}_m \to \mathrm {B} \mu _n$
classifying the
$\mathbb {G}_m \to \mathrm {B} \mu _n$
classifying the
 $\mu _n$
-torsor
$\mu _n$
-torsor
 $\mathbb {G}_m \to \mathbb {G}_m$
given by taking n-th powers induces an isomorphism
$\mathbb {G}_m \to \mathbb {G}_m$
given by taking n-th powers induces an isomorphism
 $\Sigma ^{\infty }_+\mathbb {G}_m \simeq \Sigma ^{\infty }_+\mathrm {B}\mu _n$
.
$\Sigma ^{\infty }_+\mathbb {G}_m \simeq \Sigma ^{\infty }_+\mathrm {B}\mu _n$
.
Proof. Let us consider the model for
![]() $\mathrm {B}\mathbb {G}_m$
described in (6.1.2), where
$\mathrm {B}\mathbb {G}_m$
described in (6.1.2), where
![]() $B_m\mathbb {G}_m = \mathbb {P}^{m-1}$
and
$B_m\mathbb {G}_m = \mathbb {P}^{m-1}$
and
![]() $\mathrm {B} \mathbb {G}_m = \mathbb {P}^\infty $
. Then the first statement follows from (6.1.1.i).
$\mathrm {B} \mathbb {G}_m = \mathbb {P}^\infty $
. Then the first statement follows from (6.1.1.i).
Next, consider the character
![]() $n \colon \mathbb {G}_m \to \mathbb {G}_m$
given by taking n-th powers. Its kernel is
$n \colon \mathbb {G}_m \to \mathbb {G}_m$
given by taking n-th powers. Its kernel is
![]() $\mu _n$
, and the line bundle
$\mu _n$
, and the line bundle
![]() $C_m(n)$
over
$C_m(n)$
over
![]() $B_m\mathbb {G}_m$
(defined in equation (5.3.1.a)) corresponds to the line bundle
$B_m\mathbb {G}_m$
(defined in equation (5.3.1.a)) corresponds to the line bundle
![]() $\mathcal {O}(-n)$
over
$\mathcal {O}(-n)$
over
![]() $\mathbb {P}^{m-1}$
(this may be seen for instance by combining (6.1.2) with equation (5.3.1.b)). So we are in the situation of (5.3.2) with
$\mathbb {P}^{m-1}$
(this may be seen for instance by combining (6.1.2) with equation (5.3.1.b)). So we are in the situation of (5.3.2) with
![]() $G=\mathbb {G}_m,\chi =n,H=\mu _n$
. Thus, equation (5.3.3.a) yields a distinguished triangle in
$G=\mathbb {G}_m,\chi =n,H=\mu _n$
. Thus, equation (5.3.3.a) yields a distinguished triangle in
![]() $\operatorname {\mathrm {SH}}(S)$
$\operatorname {\mathrm {SH}}(S)$
If n is odd, then
![]() $\operatorname {\mathrm {Th}}_{\mathbb {P}^\infty }(\mathcal {O}(-n))=0$
in
$\operatorname {\mathrm {Th}}_{\mathbb {P}^\infty }(\mathcal {O}(-n))=0$
in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
by (6.1.1.ii), and the above distinguished triangle shows that the morphism
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
by (6.1.1.ii), and the above distinguished triangle shows that the morphism
![]() $\Sigma ^{\infty }_+ \mathrm {B} \mu _n \to \Sigma ^{\infty }_+ \mathrm {B} \mathbb {G}_m$
is an isomorphism in
$\Sigma ^{\infty }_+ \mathrm {B} \mu _n \to \Sigma ^{\infty }_+ \mathrm {B} \mathbb {G}_m$
is an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
. Thus, the second statement follows from the first.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
. Thus, the second statement follows from the first.
Assume that n is even. Then in the diagram (5.3.4.b) the maps
![]() $i_+$
and t become isomorphisms in
$i_+$
and t become isomorphisms in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
by (6.1.1.i) and (6.1.1.iii), hence
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
by (6.1.1.i) and (6.1.1.iii), hence
![]() $\Sigma ^{\infty }_+ j \colon \Sigma ^{\infty }_+ \mathbb {G}_m \to \Sigma ^{\infty }_+ \mathrm {B} \mu _n$
is also one. As observed in (5.3.2), the latter is induced by the
$\Sigma ^{\infty }_+ j \colon \Sigma ^{\infty }_+ \mathbb {G}_m \to \Sigma ^{\infty }_+ \mathrm {B} \mu _n$
is also one. As observed in (5.3.2), the latter is induced by the
![]() $\mu _n$
-torsor
$\mu _n$
-torsor
![]() $n\colon \mathbb {G}_m \to \mathbb {G}_m$
.
$n\colon \mathbb {G}_m \to \mathbb {G}_m$
.
6.2
 $\operatorname {\mathrm {SL}}$
versus
$\operatorname {\mathrm {SL}}$
versus
 $\operatorname {\mathrm {SL}}^c$
$\operatorname {\mathrm {SL}}^c$
Let
![]() $n \in \mathbb {N} \smallsetminus \{0\}$
. Consider the character
$n \in \mathbb {N} \smallsetminus \{0\}$
. Consider the character
By definition (see [Reference Panin and WalterPW18, §3]), we have
![]() $\operatorname {\mathrm {SL}}_n^c = \ker \nu _n$
. We view
$\operatorname {\mathrm {SL}}_n^c = \ker \nu _n$
. We view
![]() $\operatorname {\mathrm {SL}}_n$
as a subgroup of
$\operatorname {\mathrm {SL}}_n$
as a subgroup of
![]() $\operatorname {\mathrm {SL}}^c_n$
via the mapping
$\operatorname {\mathrm {SL}}^c_n$
via the mapping
![]() $M \mapsto (M,1)$
.
$M \mapsto (M,1)$
.
Proposition 6.2.1. For
![]() $n \in \mathbb {N}\smallsetminus \{0\}$
, the inclusion
$n \in \mathbb {N}\smallsetminus \{0\}$
, the inclusion
![]() $\operatorname {\mathrm {SL}}_n \subset \operatorname {\mathrm {SL}}_n^c$
induces an isomorphism
$\operatorname {\mathrm {SL}}_n \subset \operatorname {\mathrm {SL}}_n^c$
induces an isomorphism
Proof. The character
is surjective (recall that
![]() $n \geq 1$
), and satisfies
$n \geq 1$
), and satisfies
![]() $\operatorname {\mathrm {SL}}_n = \ker \delta _n$
.
$\operatorname {\mathrm {SL}}_n = \ker \delta _n$
.
Set
![]() $P_n=\operatorname {\mathrm {GL}}_n \times \mathbb {G}_m$
, and denote by
$P_n=\operatorname {\mathrm {GL}}_n \times \mathbb {G}_m$
, and denote by
![]() $q_n\colon P_n \to \mathbb {G}_m$
the second projection. Let us fix an arbitrary model for
$q_n\colon P_n \to \mathbb {G}_m$
the second projection. Let us fix an arbitrary model for
![]() $\operatorname {\mathrm {BGL}}_n$
, but choose the model for
$\operatorname {\mathrm {BGL}}_n$
, but choose the model for
![]() $\mathrm {B}\mathbb {G}_m$
described in (6.1.2) so that
$\mathrm {B}\mathbb {G}_m$
described in (6.1.2) so that
![]() $B_m \mathbb {G}_m=\mathbb {P}^{m-1}$
. Recall from (5.2.1.a) that this yields a model for
$B_m \mathbb {G}_m=\mathbb {P}^{m-1}$
. Recall from (5.2.1.a) that this yields a model for
![]() $\mathrm {B} P_n$
such that
$\mathrm {B} P_n$
such that
Letting
![]() $g_n \colon P_n \to \operatorname {\mathrm {GL}}_n$
be the first projection, we have, as characters
$g_n \colon P_n \to \operatorname {\mathrm {GL}}_n$
be the first projection, we have, as characters
![]() $P_n \to \mathbb {G}_m$
$P_n \to \mathbb {G}_m$
where
![]() $\det _n \colon \operatorname {\mathrm {GL}}_n \to \mathbb {G}_m$
denotes the determinant morphism. It follows from equations (5.3.1.b) and (5.3.1.d) that, as line bundles over
$\det _n \colon \operatorname {\mathrm {GL}}_n \to \mathbb {G}_m$
denotes the determinant morphism. It follows from equations (5.3.1.b) and (5.3.1.d) that, as line bundles over
![]() $B_m P_n$
, we have in the notation of (5.3.1.a)
$B_m P_n$
, we have in the notation of (5.3.1.a)
Recall from (6.1.2) that the line bundle
![]() $C_m(\operatorname {\mathrm {id}}_{\mathbb {G}_m}) \to B_m\mathbb {G}_m$
corresponds to
$C_m(\operatorname {\mathrm {id}}_{\mathbb {G}_m}) \to B_m\mathbb {G}_m$
corresponds to
![]() $\mathcal {O}(-1) \to \mathbb {P}^{m-1}$
. Applying (4.1.5) to the projective bundle
$\mathcal {O}(-1) \to \mathbb {P}^{m-1}$
. Applying (4.1.5) to the projective bundle
![]() $B_mP_n \to B_m \operatorname {\mathrm {GL}}_n$
, for m even we have
$B_mP_n \to B_m \operatorname {\mathrm {GL}}_n$
, for m even we have
Since the character
![]() $\delta _n$
is the restriction of
$\delta _n$
is the restriction of
![]() $q_n \colon P_n \to \mathbb {G}_m$
, it follows from equation (5.3.1.c) that the line bundle
$q_n \colon P_n \to \mathbb {G}_m$
, it follows from equation (5.3.1.c) that the line bundle
![]() $C_m(\delta _n)$
over
$C_m(\delta _n)$
over
![]() $B_m\operatorname {\mathrm {SL}}_n^c$
is the pullback of
$B_m\operatorname {\mathrm {SL}}_n^c$
is the pullback of
![]() $C_m(q_n)$
over
$C_m(q_n)$
over
![]() $B_mP_n$
. By (5.3.2.c), we have a distinguished triangle in
$B_mP_n$
. By (5.3.2.c), we have a distinguished triangle in
![]() $\operatorname {\mathrm {SH}}(S)$
$\operatorname {\mathrm {SH}}(S)$
 $$ \begin{align*} \operatorname{\mathrm{Th}}_{B_m\operatorname{\mathrm{SL}}_n^c}(C_m(\delta_n)) \to \operatorname{\mathrm{Th}}_{B_mP_n}(C_m(q_n)) \to& \operatorname{\mathrm{Th}}_{B_mP_n}(C_m(\nu_n) \oplus C_m(q_n)) \\ &\quad \quad \to \Sigma^{1,0}\operatorname{\mathrm{Th}}_{B_m\operatorname{\mathrm{SL}}_n^c}(C_m(\delta_n)) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Th}}_{B_m\operatorname{\mathrm{SL}}_n^c}(C_m(\delta_n)) \to \operatorname{\mathrm{Th}}_{B_mP_n}(C_m(q_n)) \to& \operatorname{\mathrm{Th}}_{B_mP_n}(C_m(\nu_n) \oplus C_m(q_n)) \\ &\quad \quad \to \Sigma^{1,0}\operatorname{\mathrm{Th}}_{B_m\operatorname{\mathrm{SL}}_n^c}(C_m(\delta_n)) \end{align*} $$
so that, in view of equation (6.2.1.a)
Now, the distinguished triangle in
![]() $\operatorname {\mathrm {SH}}(S)$
(see (5.3.2.b))
$\operatorname {\mathrm {SH}}(S)$
(see (5.3.2.b))
implies that, for m even, the natural map induces an isomorphism
The statement follows by taking the homotopy colimit.
Remark 6.2.2. Let
![]() $A \in \operatorname {\mathrm {SH}}(S)$
be an
$A \in \operatorname {\mathrm {SH}}(S)$
be an
![]() $\eta $
-periodic commutative ring spectrum, and consider the corresponding cohomology theory
$\eta $
-periodic commutative ring spectrum, and consider the corresponding cohomology theory
![]() $A^{*,*}(-)$
(see (3.1.1)). Then by (6.2.1), we have a natural isomorphism
$A^{*,*}(-)$
(see (3.1.1)). Then by (6.2.1), we have a natural isomorphism
If A is
![]() $\operatorname {\mathrm {SL}}$
-oriented (see (3.2.5)) and
$\operatorname {\mathrm {SL}}$
-oriented (see (3.2.5)) and
![]() $S=\operatorname {\mathrm {Spec}} k$
with k a field of characteristic not two, Ananyevskiy computed in [Reference AnanyevskiyAna15, Theorem 10] that
$S=\operatorname {\mathrm {Spec}} k$
with k a field of characteristic not two, Ananyevskiy computed in [Reference AnanyevskiyAna15, Theorem 10] that
 $$\begin{align*}A^{*,*}(\operatorname{\mathrm{BSL}}_n) = \begin{cases} A^{*,*}(S)[[p_1,\ldots,p_{r-1},e]]_h & \text{if } n=2r \text{ with } r\in\mathbb{N} \smallsetminus \{0\}\\ A^{*,*}(S)[[p_1,\ldots,p_r]]_h & \text{if } n=2r+1 \text{ with } r\in \mathbb{N}, \end{cases} \end{align*}$$
$$\begin{align*}A^{*,*}(\operatorname{\mathrm{BSL}}_n) = \begin{cases} A^{*,*}(S)[[p_1,\ldots,p_{r-1},e]]_h & \text{if } n=2r \text{ with } r\in\mathbb{N} \smallsetminus \{0\}\\ A^{*,*}(S)[[p_1,\ldots,p_r]]_h & \text{if } n=2r+1 \text{ with } r\in \mathbb{N}, \end{cases} \end{align*}$$
where
![]() $p_i$
has degree
$p_i$
has degree
![]() $(4i,2i)$
and e has degree
$(4i,2i)$
and e has degree
![]() $(2r,r)$
(here, the notation
$(2r,r)$
(here, the notation
![]() $R[[x_1,\ldots ,x_m]]_h$
refers to the homogeneous power series ring in m variables over the graded ring R; see [Reference AnanyevskiyAna15, Definition 27]). This computation remains valid (with exactly the same arguments) when S is an arbitrary noetherian scheme of finite dimension under the assumption that
$R[[x_1,\ldots ,x_m]]_h$
refers to the homogeneous power series ring in m variables over the graded ring R; see [Reference AnanyevskiyAna15, Definition 27]). This computation remains valid (with exactly the same arguments) when S is an arbitrary noetherian scheme of finite dimension under the assumption that
![]() $2$
is invertible in S. Removing that last assumption seems to require a modification of the arguments of [Reference AnanyevskiyAna15], the problem being with [Reference AnanyevskiyAna15, Lemma 6] (which is used to prove [Reference AnanyevskiyAna15, Theorem 9]).
$2$
is invertible in S. Removing that last assumption seems to require a modification of the arguments of [Reference AnanyevskiyAna15], the problem being with [Reference AnanyevskiyAna15, Lemma 6] (which is used to prove [Reference AnanyevskiyAna15, Theorem 9]).
6.3
 $\operatorname {\mathrm {GL}}$
and
$\operatorname {\mathrm {GL}}$
and
 $\operatorname {\mathrm {SL}}$
$\operatorname {\mathrm {SL}}$
In this section, we compare the classifying spaces
![]() $\operatorname {\mathrm {BGL}}_{2r}$
,
$\operatorname {\mathrm {BGL}}_{2r}$
,
![]() $\operatorname {\mathrm {BGL}}_{2r+1}$
,
$\operatorname {\mathrm {BGL}}_{2r+1}$
,
![]() $\operatorname {\mathrm {BSL}}_{2r}$
,
$\operatorname {\mathrm {BSL}}_{2r}$
,
![]() $\operatorname {\mathrm {BSL}}_{2r+1}$
.
$\operatorname {\mathrm {BSL}}_{2r+1}$
.
6.3.1
Recall that under the model for
![]() $\operatorname {\mathrm {BGL}}_n$
described in (5.1.4) for
$\operatorname {\mathrm {BGL}}_n$
described in (5.1.4) for
![]() $p=n$
, the scheme
$p=n$
, the scheme
![]() $B_m \operatorname {\mathrm {GL}}_n$
is identified with the Grassmannian
$B_m \operatorname {\mathrm {GL}}_n$
is identified with the Grassmannian
![]() $\operatorname {\mathrm {Gr}}(n,nm)$
. The closed immersion
$\operatorname {\mathrm {Gr}}(n,nm)$
. The closed immersion
![]() $\operatorname {\mathrm {Gr}}(n,nm) \to \operatorname {\mathrm {Gr}}(n+1,(n+1)m)$
mapping a subbundle
$\operatorname {\mathrm {Gr}}(n,nm) \to \operatorname {\mathrm {Gr}}(n+1,(n+1)m)$
mapping a subbundle
![]() $E \subset (1^{\oplus m})^{\oplus n}$
to
$E \subset (1^{\oplus m})^{\oplus n}$
to
![]() $E \oplus 1 \subset (1^{\oplus m})^{\oplus n} \oplus 1^{\oplus m} = (1^{\oplus m})^{\oplus n+1}$
, where the inclusion
$E \oplus 1 \subset (1^{\oplus m})^{\oplus n} \oplus 1^{\oplus m} = (1^{\oplus m})^{\oplus n+1}$
, where the inclusion
![]() $1 \subset 1^{\oplus m}$
is given by the vanishing of the last
$1 \subset 1^{\oplus m}$
is given by the vanishing of the last
![]() $m-1$
coordinates, induces a morphism
$m-1$
coordinates, induces a morphism
![]() $f_m \colon B_m \operatorname {\mathrm {GL}}_n \to B_m\operatorname {\mathrm {GL}}_{n+1}$
which is compatible with the transition maps as m varies. This yields a morphism in
$f_m \colon B_m \operatorname {\mathrm {GL}}_n \to B_m\operatorname {\mathrm {GL}}_{n+1}$
which is compatible with the transition maps as m varies. This yields a morphism in
![]() $\operatorname {\mathrm {Spc}}(S)$
$\operatorname {\mathrm {Spc}}(S)$
6.3.2
For integers
![]() $u,v,w \in \mathbb {N}$
, we denote by
$u,v,w \in \mathbb {N}$
, we denote by
![]() $\operatorname {\mathrm {Gr}}(u\subset v,w)$
the flag variety of subbundles
$\operatorname {\mathrm {Gr}}(u\subset v,w)$
the flag variety of subbundles
![]() $P \subset Q \subset 1^{\oplus w}$
with
$P \subset Q \subset 1^{\oplus w}$
with
![]() $\operatorname {\mathrm {rank}} P=u$
and
$\operatorname {\mathrm {rank}} P=u$
and
![]() $\operatorname {\mathrm {rank}} Q=v$
. Let
$\operatorname {\mathrm {rank}} Q=v$
. Let
![]() $r,s \in \mathbb {N}$
, and consider the morphisms
$r,s \in \mathbb {N}$
, and consider the morphisms
given by mapping a flag
![]() $P \subset Q$
to P, resp. Q.
$P \subset Q$
to P, resp. Q.
For
![]() $n \in \{2r,2r+1\}$
, let us denote by
$n \in \{2r,2r+1\}$
, let us denote by
![]() $\mathcal {U}_n \subset 1^{\oplus s}$
the tautological rank n subbundle over
$\mathcal {U}_n \subset 1^{\oplus s}$
the tautological rank n subbundle over
![]() $\operatorname {\mathrm {Gr}}(n,s)$
, and write
$\operatorname {\mathrm {Gr}}(n,s)$
, and write
![]() $\mathcal {Q}_n = 1^{\oplus s}/\mathcal {U}_n$
. Then the morphism p may be identified with the projective bundle
$\mathcal {Q}_n = 1^{\oplus s}/\mathcal {U}_n$
. Then the morphism p may be identified with the projective bundle
![]() $\mathbb {P}(\mathcal {Q}_{2r})$
, and the morphism q is the projective bundle
$\mathbb {P}(\mathcal {Q}_{2r})$
, and the morphism q is the projective bundle
![]() $\mathbb {P}(\mathcal {U}_{2r+1}^\vee )$
.
$\mathbb {P}(\mathcal {U}_{2r+1}^\vee )$
.
Proposition 6.3.3. The map
![]() $\operatorname {\mathrm {BGL}}_{2r} \to \operatorname {\mathrm {BGL}}_{2r+1}$
of equation (6.3.1.a) becomes an isomorphism in
$\operatorname {\mathrm {BGL}}_{2r} \to \operatorname {\mathrm {BGL}}_{2r+1}$
of equation (6.3.1.a) becomes an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
.
Proof. Let
![]() $n=2r$
. For
$n=2r$
. For
![]() $m\in \mathbb {N} \smallsetminus \{0\}$
, consider the commutative diagram in
$m\in \mathbb {N} \smallsetminus \{0\}$
, consider the commutative diagram in
![]() $\operatorname {\mathrm {Sm}}_S$
$\operatorname {\mathrm {Sm}}_S$

where the morphism
![]() $j_m$
is given by mapping
$j_m$
is given by mapping
![]() $E \subset (1^{\oplus m})^{\oplus n}$
to
$E \subset (1^{\oplus m})^{\oplus n}$
to
with the inclusion
![]() $1 \subset 1^{\oplus m}$
given by the vanishing of the
$1 \subset 1^{\oplus m}$
given by the vanishing of the
![]() $m-1$
last coordinates. Here, the morphisms
$m-1$
last coordinates. Here, the morphisms
![]() $p_m,q_m$
are the morphisms
$p_m,q_m$
are the morphisms
![]() $p,q$
described in (6.3.2) when
$p,q$
described in (6.3.2) when
![]() $s=(n+1)m$
. The morphism
$s=(n+1)m$
. The morphism
![]() $f_m$
is the one described in (6.3.1), and the morphism
$f_m$
is the one described in (6.3.1), and the morphism
![]() $g_m$
is induced by the inclusion
$g_m$
is induced by the inclusion
The morphisms of this diagram are compatible with the transition maps as m varies, induced by the inclusions
![]() $1^{\oplus m} \subset 1^{\oplus m+1}$
given by the vanishing of the last coordinate.
$1^{\oplus m} \subset 1^{\oplus m+1}$
given by the vanishing of the last coordinate.
The morphism
![]() $q_m$
is a
$q_m$
is a
![]() $\mathbb {P}^n$
-bundle, hence is an isomorphism in
$\mathbb {P}^n$
-bundle, hence is an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
by (4.1.6) (recall that
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
by (4.1.6) (recall that
![]() $n=2r$
is even). The morphism
$n=2r$
is even). The morphism
![]() $p_m$
is a
$p_m$
is a
![]() $\mathbb {P}^{(n+1)m-n-1}$
-bundle, hence is also an isomorphism in
$\mathbb {P}^{(n+1)m-n-1}$
-bundle, hence is also an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
when m is odd by (4.1.6).
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
when m is odd by (4.1.6).
In the notation of (5.1.4), the morphism
![]() $g_m$
is the
$g_m$
is the
![]() $\operatorname {\mathrm {GL}}_n$
-quotient of the morphism
$\operatorname {\mathrm {GL}}_n$
-quotient of the morphism
![]() $U_{m,n} \to U_{m,n+1}$
induced by equation (6.3.3.a). Therefore, it follows from (5.1.1) that the map
$U_{m,n} \to U_{m,n+1}$
induced by equation (6.3.3.a). Therefore, it follows from (5.1.1) that the map
![]() $\operatorname {\mathrm {colim}}_m g_m$
is a weak equivalence of motivic spaces.
$\operatorname {\mathrm {colim}}_m g_m$
is a weak equivalence of motivic spaces.
Applying the functor
![]() $\Sigma ^{\infty }_+ \colon \operatorname {\mathrm {Sm}}_S \to \operatorname {\mathrm {Spt}}(S)[\eta ^{-1}]$
to the above diagram and taking the homotopy colimit over m, we thus obtain a commutative diagram in
$\Sigma ^{\infty }_+ \colon \operatorname {\mathrm {Sm}}_S \to \operatorname {\mathrm {Spt}}(S)[\eta ^{-1}]$
to the above diagram and taking the homotopy colimit over m, we thus obtain a commutative diagram in
![]() $\operatorname {\mathrm {Spt}}(S)[\eta ^{-1}]$
, where all maps are weak equivalences. Since the map (6.3.1.a) is obtained as
$\operatorname {\mathrm {Spt}}(S)[\eta ^{-1}]$
, where all maps are weak equivalences. Since the map (6.3.1.a) is obtained as
![]() $\operatorname {\mathrm {colim}}_m f_m$
, the proposition follows.
$\operatorname {\mathrm {colim}}_m f_m$
, the proposition follows.
6.3.4
Let
![]() $n \in \mathbb {N} \smallsetminus \{0\}$
. The group
$n \in \mathbb {N} \smallsetminus \{0\}$
. The group
![]() $\operatorname {\mathrm {SL}}_n$
is the kernel of the determinant morphism
$\operatorname {\mathrm {SL}}_n$
is the kernel of the determinant morphism
![]() $\det _n \colon \operatorname {\mathrm {GL}}_n \to \mathbb {G}_m$
, which is surjective (as
$\det _n \colon \operatorname {\mathrm {GL}}_n \to \mathbb {G}_m$
, which is surjective (as
![]() $n\geq 1$
). We are thus in the situation of (5.3.2) so that we have by equation (5.3.5.a) a splitting
$n\geq 1$
). We are thus in the situation of (5.3.2) so that we have by equation (5.3.5.a) a splitting
6.3.5
Using the model for
![]() $\operatorname {\mathrm {BGL}}_n$
described in (5.1.4) with
$\operatorname {\mathrm {BGL}}_n$
described in (5.1.4) with
![]() $p=n$
, the variety
$p=n$
, the variety
![]() $B_m \operatorname {\mathrm {GL}}_n$
coincides with the Grassmannian
$B_m \operatorname {\mathrm {GL}}_n$
coincides with the Grassmannian
![]() $\operatorname {\mathrm {Gr}}(n,nm)$
. Observe that the tautological bundle
$\operatorname {\mathrm {Gr}}(n,nm)$
. Observe that the tautological bundle
![]() $\mathcal {U}_n$
over this variety is isomorphic to the quotient
$\mathcal {U}_n$
over this variety is isomorphic to the quotient
![]() $(E_m\operatorname {\mathrm {GL}}_n \times {\mathbb {A}}^n)/\operatorname {\mathrm {GL}}_n$
, where the right
$(E_m\operatorname {\mathrm {GL}}_n \times {\mathbb {A}}^n)/\operatorname {\mathrm {GL}}_n$
, where the right
![]() $\operatorname {\mathrm {GL}}_n$
-action on
$\operatorname {\mathrm {GL}}_n$
-action on
![]() ${\mathbb {A}}^n$
is given by letting
${\mathbb {A}}^n$
is given by letting
![]() $\varphi \in \operatorname {\mathrm {GL}}_n$
act via
$\varphi \in \operatorname {\mathrm {GL}}_n$
act via
![]() $v \mapsto \varphi ^{-1}(v)$
. The
$v \mapsto \varphi ^{-1}(v)$
. The
![]() $\operatorname {\mathrm {GL}}_n$
-equivariant isomorphism
$\operatorname {\mathrm {GL}}_n$
-equivariant isomorphism
![]() $\det (E_m\operatorname {\mathrm {GL}}_n \times {\mathbb {A}}^n) \simeq E_m\operatorname {\mathrm {GL}}_n \times {\mathbb {A}}^1$
, where the right
$\det (E_m\operatorname {\mathrm {GL}}_n \times {\mathbb {A}}^n) \simeq E_m\operatorname {\mathrm {GL}}_n \times {\mathbb {A}}^1$
, where the right
![]() $\operatorname {\mathrm {GL}}_n$
-action on
$\operatorname {\mathrm {GL}}_n$
-action on
![]() ${\mathbb {A}}^1$
is given by letting
${\mathbb {A}}^1$
is given by letting
![]() $\varphi \in \operatorname {\mathrm {GL}}_n$
act via
$\varphi \in \operatorname {\mathrm {GL}}_n$
act via
![]() $\lambda \mapsto \det _n(\varphi ^{-1}) \lambda $
, yields an isomorphism of line bundles over
$\lambda \mapsto \det _n(\varphi ^{-1}) \lambda $
, yields an isomorphism of line bundles over
![]() $B_m\operatorname {\mathrm {GL}}_n$
$B_m\operatorname {\mathrm {GL}}_n$
Proposition 6.3.6. Let
![]() $r \in \mathbb {N}$
. Then in
$r \in \mathbb {N}$
. Then in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, the natural morphism
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, the natural morphism
![]() $\operatorname {\mathrm {BSL}}_{2r} \to \operatorname {\mathrm {BGL}}_{2r}$
acquires a section, and the natural morphism
$\operatorname {\mathrm {BSL}}_{2r} \to \operatorname {\mathrm {BGL}}_{2r}$
acquires a section, and the natural morphism
![]() $\operatorname {\mathrm {BSL}}_{2r+1} \to \operatorname {\mathrm {BGL}}_{2r+1}$
becomes an isomorphism.
$\operatorname {\mathrm {BSL}}_{2r+1} \to \operatorname {\mathrm {BGL}}_{2r+1}$
becomes an isomorphism.
Proof. The first statement follows from (6.3.4.a). Let us prove the second. We use the model for
![]() $\operatorname {\mathrm {BGL}}_{2r+1}$
described in (5.1.4) with
$\operatorname {\mathrm {BGL}}_{2r+1}$
described in (5.1.4) with
![]() $n=p=2r+1$
so that
$n=p=2r+1$
so that
![]() $B_m \operatorname {\mathrm {GL}}_{2r+1} = \operatorname {\mathrm {Gr}}(2r+1,s)$
where
$B_m \operatorname {\mathrm {GL}}_{2r+1} = \operatorname {\mathrm {Gr}}(2r+1,s)$
where
![]() $s=(2r+1)m$
. We consider the situation of (6.3.2) and use the notation thereof. We have an exact sequence of vector bundles over
$s=(2r+1)m$
. We consider the situation of (6.3.2) and use the notation thereof. We have an exact sequence of vector bundles over
![]() $Y_m=\operatorname {\mathrm {Gr}}(2r \subset 2r+1,s)=\mathbb {P}(\mathcal {Q}_{2r})$
$Y_m=\operatorname {\mathrm {Gr}}(2r \subset 2r+1,s)=\mathbb {P}(\mathcal {Q}_{2r})$
Taking determinants and using equation (6.3.5.a), we obtain an isomorphism of line bundles
When m is even, the vector bundle
![]() $\mathcal {Q}_{2r}=1^{\oplus s}/\mathcal {U}_{2r}$
has even rank, hence it follows from (4.1.5) and equation (6.3.6.a) that
$\mathcal {Q}_{2r}=1^{\oplus s}/\mathcal {U}_{2r}$
has even rank, hence it follows from (4.1.5) and equation (6.3.6.a) that
![]() $\operatorname {\mathrm {Th}}_{Y_m}(q^*C_m(\det _{2r+1}))=0$
in
$\operatorname {\mathrm {Th}}_{Y_m}(q^*C_m(\det _{2r+1}))=0$
in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
. Since
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
. Since
![]() $q \colon Y_m \to \operatorname {\mathrm {Gr}}(2r+1,s)$
is a
$q \colon Y_m \to \operatorname {\mathrm {Gr}}(2r+1,s)$
is a
![]() $\mathbb {P}^{2r}$
-bundle, it then follows from (4.1.6) (applied with
$\mathbb {P}^{2r}$
-bundle, it then follows from (4.1.6) (applied with
![]() $V=C_m(\det _{2r+1})$
) that
$V=C_m(\det _{2r+1})$
) that
![]() $\operatorname {\mathrm {Th}}_{\operatorname {\mathrm {Gr}}(2r+1,s)}(C_m(\det _{2r+1}))=0$
in
$\operatorname {\mathrm {Th}}_{\operatorname {\mathrm {Gr}}(2r+1,s)}(C_m(\det _{2r+1}))=0$
in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
for m even. Taking the homotopy colimit over m, we deduce that
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
for m even. Taking the homotopy colimit over m, we deduce that
![]() $\operatorname {\mathrm {Th}}_{\operatorname {\mathrm {BGL}}_{2r+1}}(C(\det _{2r+1}))=0$
in
$\operatorname {\mathrm {Th}}_{\operatorname {\mathrm {BGL}}_{2r+1}}(C(\det _{2r+1}))=0$
in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, and the second statement of the proposition follows from equation (6.3.4.a).
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, and the second statement of the proposition follows from equation (6.3.4.a).
Remark 6.3.7. Let
![]() $A \in \operatorname {\mathrm {SH}}(S)$
be an
$A \in \operatorname {\mathrm {SH}}(S)$
be an
![]() $\eta $
-periodic
$\eta $
-periodic
![]() $\operatorname {\mathrm {SL}}$
-oriented commutative ring spectrum (see (3.2.5)), and consider the corresponding cohomology theory
$\operatorname {\mathrm {SL}}$
-oriented commutative ring spectrum (see (3.2.5)), and consider the corresponding cohomology theory
![]() $A^{*,*}(-)$
(see (3.1.1)). Assume that
$A^{*,*}(-)$
(see (3.1.1)). Assume that
![]() $2$
is invertible in S. Combining (6.3.6) and (6.3.3) with Ananyevskiy’s computation of
$2$
is invertible in S. Combining (6.3.6) and (6.3.3) with Ananyevskiy’s computation of
![]() $A^{*,*}(\operatorname {\mathrm {BSL}}_{2r+1})$
(see (6.2.2)), we recover Levine’s computation [Reference LevineLev19, Theorem 4.1]
$A^{*,*}(\operatorname {\mathrm {BSL}}_{2r+1})$
(see (6.2.2)), we recover Levine’s computation [Reference LevineLev19, Theorem 4.1]
(Note that this permits to remove some of the technical assumptions present in the statement of [Reference LevineLev19, Theorem 4.1].)
Appendix A An invariant of
 $\mu _2$
-torsors
$\mu _2$
-torsors
We have proved in (6.1.3) that in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, for
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, for
![]() $n\in \mathbb {N}$
$n\in \mathbb {N}$
 $$\begin{align*}\Sigma^{\infty}_+ \mathrm{B} \mu_n = \begin{cases} \mathbf{1}_S & \text{if } n=0 (\text{i.e., } \mu_n = \mathbb{G}_m) \text{ or } n \text{ is odd,}\\ \Sigma^{\infty}_+ \mathbb{G}_m = \mathbf{1}_S \oplus \mathbf{1}_S & \text{if } n>0 \text{ is even.} \end{cases} \end{align*}$$
$$\begin{align*}\Sigma^{\infty}_+ \mathrm{B} \mu_n = \begin{cases} \mathbf{1}_S & \text{if } n=0 (\text{i.e., } \mu_n = \mathbb{G}_m) \text{ or } n \text{ is odd,}\\ \Sigma^{\infty}_+ \mathbb{G}_m = \mathbf{1}_S \oplus \mathbf{1}_S & \text{if } n>0 \text{ is even.} \end{cases} \end{align*}$$
Thus, when
![]() $n>0$
is even, there is essentially one nontrivial invariant of
$n>0$
is even, there is essentially one nontrivial invariant of
![]() $\mu _n$
-torsors over S in
$\mu _n$
-torsors over S in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, in the form of an element of
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
, in the form of an element of
![]() $\operatorname {\mathrm {End}}_{\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]}(\mathbf {1}_S)$
. Moreover, it also follows from (6.1.3) that the morphism
$\operatorname {\mathrm {End}}_{\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]}(\mathbf {1}_S)$
. Moreover, it also follows from (6.1.3) that the morphism
![]() $\mathrm {B} \mu _2 \to \mathrm {B} \mu _{2r}$
becomes an isomorphism in
$\mathrm {B} \mu _2 \to \mathrm {B} \mu _{2r}$
becomes an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
for
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
for
![]() $r>0$
. Therefore, the above-mentioned invariant of
$r>0$
. Therefore, the above-mentioned invariant of
![]() $\mu _n$
-torsors is induced by an invariant of
$\mu _n$
-torsors is induced by an invariant of
![]() $\mu _2$
-torsors, which is, however, not really explicit from this description. In this section, we provide an explicit construction of this invariant (the connection with the above discussion is made in (A.9) below).
$\mu _2$
-torsors, which is, however, not really explicit from this description. In this section, we provide an explicit construction of this invariant (the connection with the above discussion is made in (A.9) below).
A.1
Let
![]() $L\to S$
be a line bundle. As observed by Ananyevskiy [Reference AnanyevskiyAna20, Lemma 4.1], the isomorphism of S-schemes
$L\to S$
be a line bundle. As observed by Ananyevskiy [Reference AnanyevskiyAna20, Lemma 4.1], the isomorphism of S-schemes
![]() $L^\circ \xrightarrow {\sim } (L^\vee )^\circ $
, given locally by
$L^\circ \xrightarrow {\sim } (L^\vee )^\circ $
, given locally by
![]() $l \mapsto l^\vee $
, where
$l \mapsto l^\vee $
, where
![]() $l^\vee (l)=1$
, induces an isomorphism in
$l^\vee (l)=1$
, induces an isomorphism in
![]() $H_{\bullet }(S)$
$H_{\bullet }(S)$
A.2
If
![]() $\varphi \colon L \to M$
is an isomorphism of line bundles over X, we have (see (1.5))
$\varphi \colon L \to M$
is an isomorphism of line bundles over X, we have (see (1.5))
Definition A.3. It will be convenient to think of a
![]() $\mu _2$
-torsor over S as a pair
$\mu _2$
-torsor over S as a pair
![]() $(L,\lambda )$
, where
$(L,\lambda )$
, where
![]() $L\to S$
is a line bundle, and
$L\to S$
is a line bundle, and
![]() $\lambda \colon L \xrightarrow {\sim } L^\vee $
is an isomorphism of line bundles over S. Isomorphisms
$\lambda \colon L \xrightarrow {\sim } L^\vee $
is an isomorphism of line bundles over S. Isomorphisms
![]() $(L,\lambda ) \to (L',\lambda ')$
are given by isomorphisms of line bundles
$(L,\lambda ) \to (L',\lambda ')$
are given by isomorphisms of line bundles
![]() $\varphi \colon L \xrightarrow {\sim } L'$
such that
$\varphi \colon L \xrightarrow {\sim } L'$
such that
![]() $\lambda = \varphi ^\vee \circ \lambda ' \circ \varphi $
. The set of isomorphism classes of
$\lambda = \varphi ^\vee \circ \lambda ' \circ \varphi $
. The set of isomorphism classes of
![]() $\mu _2$
-torsors is denoted
$\mu _2$
-torsors is denoted
![]() $H^1_{et}(S,\mu _2)$
; it is endowed with a group structure induced by the tensor product of line bundles.
$H^1_{et}(S,\mu _2)$
; it is endowed with a group structure induced by the tensor product of line bundles.
Definition A.4. Consider a
![]() $\mu _2$
-torsor, given by a line bundle
$\mu _2$
-torsor, given by a line bundle
![]() $L\to S$
and an isomorphism
$L\to S$
and an isomorphism
![]() $\lambda \colon L\xrightarrow {\sim } L^\vee $
. Let us consider the composite isomorphism in
$\lambda \colon L\xrightarrow {\sim } L^\vee $
. Let us consider the composite isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)$
(see (A.1) for the definition of
$\operatorname {\mathrm {SH}}(S)$
(see (A.1) for the definition of
![]() $\sigma _L$
, and (1.5) for that of
$\sigma _L$
, and (1.5) for that of
![]() $\operatorname {\mathrm {Th}}(\lambda )$
)
$\operatorname {\mathrm {Th}}(\lambda )$
)
This yields an element
![]() $a_{(L,\lambda )} = \Sigma ^{-L}(\sigma _L^{-1} \circ \operatorname {\mathrm {Th}}(\lambda )) \in \operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {SH}}(S)}(\mathbf {1}_S)$
. We define
$a_{(L,\lambda )} = \Sigma ^{-L}(\sigma _L^{-1} \circ \operatorname {\mathrm {Th}}(\lambda )) \in \operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {SH}}(S)}(\mathbf {1}_S)$
. We define
where
![]() $\operatorname {\mathrm {can}} \colon 1 \to 1^\vee $
is the canonical isomorphism of line bundles over S. (The element
$\operatorname {\mathrm {can}} \colon 1 \to 1^\vee $
is the canonical isomorphism of line bundles over S. (The element
![]() $a_{(1,\operatorname {\mathrm {can}})}$
corresponds to the element
$a_{(1,\operatorname {\mathrm {can}})}$
corresponds to the element
![]() $\epsilon $
of [Reference MorelMor04, §6.1].)
$\epsilon $
of [Reference MorelMor04, §6.1].)
A.5
This construction is compatible with pullbacks, in the sense that if
![]() $f\colon R \to S$
is a morphism of noetherian schemes of finite dimension and
$f\colon R \to S$
is a morphism of noetherian schemes of finite dimension and
![]() $(L,\lambda )$
a
$(L,\lambda )$
a
![]() $\mu _2$
-torsor, then the composite in
$\mu _2$
-torsor, then the composite in
![]() $\operatorname {\mathrm {SH}}(R)$
$\operatorname {\mathrm {SH}}(R)$
is
![]() $\alpha (f^*L,f^*\lambda )$
.
$\alpha (f^*L,f^*\lambda )$
.
Example A.6. Consider a
![]() $\mu _2$
-torsor
$\mu _2$
-torsor
![]() $(L,\lambda )$
, where
$(L,\lambda )$
, where
![]() $L=1$
is the trivial line bundle. Then
$L=1$
is the trivial line bundle. Then
![]() $\lambda = u \operatorname {\mathrm {can}}$
for some
$\lambda = u \operatorname {\mathrm {can}}$
for some
![]() $u \in H^0(S,\mathbb {G}_m)$
, hence
$u \in H^0(S,\mathbb {G}_m)$
, hence
![]() $\operatorname {\mathrm {Th}}(\lambda ) = \operatorname {\mathrm {Th}}(\operatorname {\mathrm {can}}) \circ \operatorname {\mathrm {Th}}(u\operatorname {\mathrm {id}}_1)$
. Therefore, (see (1.6))
$\operatorname {\mathrm {Th}}(\lambda ) = \operatorname {\mathrm {Th}}(\operatorname {\mathrm {can}}) \circ \operatorname {\mathrm {Th}}(u\operatorname {\mathrm {id}}_1)$
. Therefore, (see (1.6))
 $$ \begin{align*} \alpha(1,\lambda) &= \Sigma^{-2,-1}((\sigma_1^{-1} \circ \operatorname{\mathrm{Th}}(\operatorname{\mathrm{can}}))^{-1} \circ (\sigma_1^{-1} \circ \operatorname{\mathrm{Th}}(\lambda)) \\ &= \Sigma^{-2,-1}(\operatorname{\mathrm{Th}}(\operatorname{\mathrm{can}})^{-1} \circ \operatorname{\mathrm{Th}}(\lambda))\\ &= \Sigma^{-2,-1} \operatorname{\mathrm{Th}}(u\operatorname{\mathrm{id}}_1)\\ &= \langle u\rangle. \end{align*} $$
$$ \begin{align*} \alpha(1,\lambda) &= \Sigma^{-2,-1}((\sigma_1^{-1} \circ \operatorname{\mathrm{Th}}(\operatorname{\mathrm{can}}))^{-1} \circ (\sigma_1^{-1} \circ \operatorname{\mathrm{Th}}(\lambda)) \\ &= \Sigma^{-2,-1}(\operatorname{\mathrm{Th}}(\operatorname{\mathrm{can}})^{-1} \circ \operatorname{\mathrm{Th}}(\lambda))\\ &= \Sigma^{-2,-1} \operatorname{\mathrm{Th}}(u\operatorname{\mathrm{id}}_1)\\ &= \langle u\rangle. \end{align*} $$
Proposition A.7. The assignment
![]() $(L,\lambda ) \mapsto \alpha (L,\lambda )$
induces a morphism of pointed sets
$(L,\lambda ) \mapsto \alpha (L,\lambda )$
induces a morphism of pointed sets
Proof. By construction, we have
![]() $\alpha (1,\operatorname {\mathrm {can}})=\operatorname {\mathrm {id}}$
. Consider an isomorphism of
$\alpha (1,\operatorname {\mathrm {can}})=\operatorname {\mathrm {id}}$
. Consider an isomorphism of
![]() $\mu _2$
-torsors
$\mu _2$
-torsors
![]() $(L,\lambda ) \xrightarrow {\sim } (M,\mu )$
(see (A.3)), given by an isomorphism
$(L,\lambda ) \xrightarrow {\sim } (M,\mu )$
(see (A.3)), given by an isomorphism
![]() $\varphi \colon L \xrightarrow {\sim } M$
. Let us set
$\varphi \colon L \xrightarrow {\sim } M$
. Let us set
![]() $a_L = a_{(L,\lambda )}$
and
$a_L = a_{(L,\lambda )}$
and
![]() $a_M = a_{(M,\mu )}$
(see (A.4)). Then, in
$a_M = a_{(M,\mu )}$
(see (A.4)). Then, in
![]() $\operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {SH}}(S)}(\operatorname {\mathrm {Th}}_S(L))$
,
$\operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {SH}}(S)}(\operatorname {\mathrm {Th}}_S(L))$
,
 $$ \begin{align*} \Sigma^La_L = \sigma_L^{-1} \circ \operatorname{\mathrm{Th}}(\lambda) &= \sigma_L^{-1} \circ \operatorname{\mathrm{Th}}(\varphi^\vee) \circ \operatorname{\mathrm{Th}}(\mu) \circ \operatorname{\mathrm{Th}}(\varphi) && \text{(as } \lambda = \varphi^\vee \circ \mu \circ \varphi) \\ &= \operatorname{\mathrm{Th}}(\varphi)^{-1} \circ \sigma_M^{-1} \circ \operatorname{\mathrm{Th}}(\mu) \circ \operatorname{\mathrm{Th}}(\varphi) && \text{by equation (A.2.a)}\\ &= \operatorname{\mathrm{Th}}(\varphi)^{-1} \circ (\Sigma^Ma_M) \circ \operatorname{\mathrm{Th}}(\varphi) \\ &= \operatorname{\mathrm{Th}}(\varphi)^{-1} \circ \operatorname{\mathrm{Th}}(\varphi) \circ (\Sigma^L a_M) && \text{(by equation (1.5.b))}\\ &= \Sigma^La_M, \end{align*} $$
$$ \begin{align*} \Sigma^La_L = \sigma_L^{-1} \circ \operatorname{\mathrm{Th}}(\lambda) &= \sigma_L^{-1} \circ \operatorname{\mathrm{Th}}(\varphi^\vee) \circ \operatorname{\mathrm{Th}}(\mu) \circ \operatorname{\mathrm{Th}}(\varphi) && \text{(as } \lambda = \varphi^\vee \circ \mu \circ \varphi) \\ &= \operatorname{\mathrm{Th}}(\varphi)^{-1} \circ \sigma_M^{-1} \circ \operatorname{\mathrm{Th}}(\mu) \circ \operatorname{\mathrm{Th}}(\varphi) && \text{by equation (A.2.a)}\\ &= \operatorname{\mathrm{Th}}(\varphi)^{-1} \circ (\Sigma^Ma_M) \circ \operatorname{\mathrm{Th}}(\varphi) \\ &= \operatorname{\mathrm{Th}}(\varphi)^{-1} \circ \operatorname{\mathrm{Th}}(\varphi) \circ (\Sigma^L a_M) && \text{(by equation (1.5.b))}\\ &= \Sigma^La_M, \end{align*} $$
whence
![]() $a_L = a_M$
, and
$a_L = a_M$
, and
![]() $\alpha (L,\lambda ) = \alpha (M,\mu )$
.
$\alpha (L,\lambda ) = \alpha (M,\mu )$
.
Proposition A.8. The assignment
![]() $(L,\lambda ) \mapsto \alpha (L,\lambda )$
induces a group morphism
$(L,\lambda ) \mapsto \alpha (L,\lambda )$
induces a group morphism
Proof. Consider
![]() $\mu _2$
-torsors given by line bundles
$\mu _2$
-torsors given by line bundles
![]() $L,M$
over S and isomorphisms
$L,M$
over S and isomorphisms
![]() $L\xrightarrow {\sim } L^\vee $
and
$L\xrightarrow {\sim } L^\vee $
and
![]() $M \xrightarrow {\sim } M^\vee $
. As the functor
$M \xrightarrow {\sim } M^\vee $
. As the functor
![]() $f^* \colon \operatorname {\mathrm {SH}}(S)[\eta ^{-1}] \to \operatorname {\mathrm {SH}}(L^\circ )[\eta ^{-1}]$
is faithful (2.2.8), by functoriality (A.5) we may assume that the line bundle L is trivial. Similarly, we may assume that M is also trivial. By (A.7), we may assume that
$f^* \colon \operatorname {\mathrm {SH}}(S)[\eta ^{-1}] \to \operatorname {\mathrm {SH}}(L^\circ )[\eta ^{-1}]$
is faithful (2.2.8), by functoriality (A.5) we may assume that the line bundle L is trivial. Similarly, we may assume that M is also trivial. By (A.7), we may assume that
![]() $L=M=1$
. Then, in view of (A.6), the statement follows from equation (1.6.a).
$L=M=1$
. Then, in view of (A.6), the statement follows from equation (1.6.a).
Remark A.9. Let
![]() $\rho \colon \mathbb {G}_m \to \mathrm {B} \mu _2$
be the map classifying the
$\rho \colon \mathbb {G}_m \to \mathrm {B} \mu _2$
be the map classifying the
![]() $\mu _2$
-torsor
$\mu _2$
-torsor
![]() $(1,t\operatorname {\mathrm {id}})$
over
$(1,t\operatorname {\mathrm {id}})$
over
![]() $\mathbb {G}_m$
, where
$\mathbb {G}_m$
, where
![]() $t\in H^0(\mathbb {G}_m,\mathbb {G}_m)$
is the tautological section. Recall from (6.1.3.iii) that
$t\in H^0(\mathbb {G}_m,\mathbb {G}_m)$
is the tautological section. Recall from (6.1.3.iii) that
![]() $\Sigma ^{\infty }_+ \rho \colon \Sigma ^{\infty }_+ \mathbb {G}_m \to \Sigma ^{\infty }_+ \mathrm {B} \mu _2$
is an isomorphism in
$\Sigma ^{\infty }_+ \rho \colon \Sigma ^{\infty }_+ \mathbb {G}_m \to \Sigma ^{\infty }_+ \mathrm {B} \mu _2$
is an isomorphism in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
. If a
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
. If a
![]() $\mu _2$
-torsor
$\mu _2$
-torsor
![]() $(L,\lambda )$
is classified by the map
$(L,\lambda )$
is classified by the map
![]() $f \colon S \to \mathrm {B} \mu _2$
, we claim that
$f \colon S \to \mathrm {B} \mu _2$
, we claim that
![]() $\alpha (L,\lambda )$
is the composite in
$\alpha (L,\lambda )$
is the composite in
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
(the map
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]$
(the map
![]() $\pi _1$
was defined in (2.2.1))
$\pi _1$
was defined in (2.2.1))
Indeed, applying the functor
![]() $\operatorname {\mathrm {SH}}(S)[\eta ^{-1}] \to \operatorname {\mathrm {SH}}(L^\circ )[\eta ^{-1}]$
which is faithful by (2.2.8) and using (A.7), we may assume that
$\operatorname {\mathrm {SH}}(S)[\eta ^{-1}] \to \operatorname {\mathrm {SH}}(L^\circ )[\eta ^{-1}]$
which is faithful by (2.2.8) and using (A.7), we may assume that
![]() $L=1$
. Then
$L=1$
. Then
![]() $\lambda $
is given by multiplication by an element
$\lambda $
is given by multiplication by an element
![]() $u \in H^0(S,\mathbb {G}_m)$
, and the map f factors as
$u \in H^0(S,\mathbb {G}_m)$
, and the map f factors as
![]() $S \xrightarrow {u} \mathbb {G}_m \xrightarrow {\rho } \mathrm {B} \mu _2$
. Denoting by
$S \xrightarrow {u} \mathbb {G}_m \xrightarrow {\rho } \mathrm {B} \mu _2$
. Denoting by
![]() $p \colon \mathbb {G}_m \to S$
is the projection, the composite (A.9.a) is given by
$p \colon \mathbb {G}_m \to S$
is the projection, the composite (A.9.a) is given by
which coincides with
![]() $\langle u \rangle \in \operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]}(S)$
. Thus, the claim follows from (A.6).
$\langle u \rangle \in \operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {SH}}(S)[\eta ^{-1}]}(S)$
. Thus, the claim follows from (A.6).
Acknowledgments
I am grateful to the referee for his/her suggestions and in particular for noticing that the coequaliser diagram of (2.2.7) is split.
This work was supported by the DFG research grant HA 7702/5-1 and Heisenberg grant HA 7702/4-1.
Competing interests
The authors have no competing interest to declare.