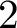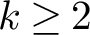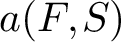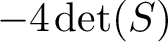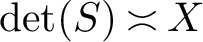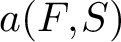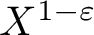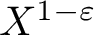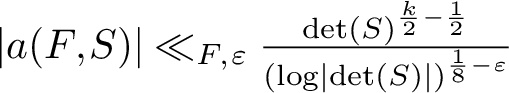1. Introduction
Let
 $S_k(\Gamma _0^{(2)}(N))$
denote the space of Siegel cusp forms of degree
$S_k(\Gamma _0^{(2)}(N))$
denote the space of Siegel cusp forms of degree
![]() $2$
and weight k with respect to the congruence subgroup
$2$
and weight k with respect to the congruence subgroup
 $\Gamma _0^{(2)}(N) \subseteq \mathrm {Sp}_4({\mathbb Z})$
of level N. Any
$\Gamma _0^{(2)}(N) \subseteq \mathrm {Sp}_4({\mathbb Z})$
of level N. Any
 $F \in S_k(\Gamma _0^{(2)}(N))$
has a Fourier expansion of the form
$F \in S_k(\Gamma _0^{(2)}(N))$
has a Fourier expansion of the form
 $$ \begin{align} F(Z)=\sum_{S\in \Lambda_2} a(F, S)e^{2\pi i{\mathrm{Tr}}(SZ)},\qquad Z\text{ in the Siegel upper half-space}, \end{align} $$
$$ \begin{align} F(Z)=\sum_{S\in \Lambda_2} a(F, S)e^{2\pi i{\mathrm{Tr}}(SZ)},\qquad Z\text{ in the Siegel upper half-space}, \end{align} $$
where the set
![]() $\Lambda _2$
consists of symmetric, semi-integral, positive-definite
$\Lambda _2$
consists of symmetric, semi-integral, positive-definite
![]() $2\times 2$
matrices S – that is,
$2\times 2$
matrices S – that is,
 $$ \begin{align} \Lambda_2 = \left\{{\left(\begin{array}{@{}cc@{}}a&b/2\\b/2&c\end{array}\right)},\qquad a,b,c\in{\mathbb Z}, \qquad a>0, \qquad d:=b^2 - 4ac <0\right\}. \end{align} $$
$$ \begin{align} \Lambda_2 = \left\{{\left(\begin{array}{@{}cc@{}}a&b/2\\b/2&c\end{array}\right)},\qquad a,b,c\in{\mathbb Z}, \qquad a>0, \qquad d:=b^2 - 4ac <0\right\}. \end{align} $$
For
 $S ={\left (\begin {array}{@{}cc@{}}a&b/2\\b/2&c\end {array}\right )}\in \Lambda _2$
, we define
$S ={\left (\begin {array}{@{}cc@{}}a&b/2\\b/2&c\end {array}\right )}\in \Lambda _2$
, we define
![]() ${\mathrm{disc}}(S)=-4\det (S)=b^2-4ac$
. If
${\mathrm{disc}}(S)=-4\det (S)=b^2-4ac$
. If
![]() $d = {\mathrm{disc}}(S)$
is a fundamental discriminant,Footnote
1
then S is called fundamental. A fundamental S is automatically primitive (i.e.,
$d = {\mathrm{disc}}(S)$
is a fundamental discriminant,Footnote
1
then S is called fundamental. A fundamental S is automatically primitive (i.e.,
![]() $\gcd (a,b,c)=1$
). Observe that if d is odd, then S is fundamental if and only if d is square-free. The fundamental Fourier coefficients of Siegel cusp forms are deep and highly interesting objects. These are the basic building blocks, in the sense that one cannot use the theory of Hecke operators to relate the Fourier coefficients
$\gcd (a,b,c)=1$
). Observe that if d is odd, then S is fundamental if and only if d is square-free. The fundamental Fourier coefficients of Siegel cusp forms are deep and highly interesting objects. These are the basic building blocks, in the sense that one cannot use the theory of Hecke operators to relate the Fourier coefficients
![]() $a(F,S)$
at these matrices to those at simpler matrices. Furthermore, fundamental Fourier coefficients are closely related to central L-values.
$a(F,S)$
at these matrices to those at simpler matrices. Furthermore, fundamental Fourier coefficients are closely related to central L-values.
In [Reference Saha56, Reference Schmidt58] it was proved that if
![]() $k>2$
is even and N is square-free, then elements of
$k>2$
is even and N is square-free, then elements of
 $S_k(\Gamma _0^{(2)}(N))$
(under some mild assumptions) are uniquely determined by their fundamental Fourier coefficients. More precisely, it was proved there that for
$S_k(\Gamma _0^{(2)}(N))$
(under some mild assumptions) are uniquely determined by their fundamental Fourier coefficients. More precisely, it was proved there that for
![]() $k,\ N$
as described, if
$k,\ N$
as described, if
 $F \in S_k(\Gamma _0^{(2)}(N))$
is nonzero and an eigenfunction of the
$F \in S_k(\Gamma _0^{(2)}(N))$
is nonzero and an eigenfunction of the
![]() $U(p)$
operators for
$U(p)$
operators for
![]() $p\mid N$
, then
$p\mid N$
, then
![]() $a(F, S) \ne 0$
for infinitely many matrices S such that
$a(F, S) \ne 0$
for infinitely many matrices S such that
![]() ${\mathrm{disc}}(S)$
is odd and square-free. This nonvanishing result is crucial for the existence of good Bessel models [Reference Prasad and Ramakrishnan44, Lemma 5.1.1], and consequently was needed for removing a key assumption from theorems due to Furusawa [Reference Furusawa and Morimoto17], Pitale and Schmidt [Reference Pitale and Schmidt46], and the third named author of the present paper [Reference Prasad and Ramakrishnan44, Reference Saha54, Reference Saha55] on the degree
${\mathrm{disc}}(S)$
is odd and square-free. This nonvanishing result is crucial for the existence of good Bessel models [Reference Prasad and Ramakrishnan44, Lemma 5.1.1], and consequently was needed for removing a key assumption from theorems due to Furusawa [Reference Furusawa and Morimoto17], Pitale and Schmidt [Reference Pitale and Schmidt46], and the third named author of the present paper [Reference Prasad and Ramakrishnan44, Reference Saha54, Reference Saha55] on the degree
![]() $8\ L$
-function on
$8\ L$
-function on
![]() ${\mathrm{GSp}}_4 \times {\mathrm{GL}}_2$
. Furthermore, there is a remarkable identity, explained in more detail in §1.3, relating squares of (weighted averages of) fundamental Fourier coefficients and central values of dihedral twists of
${\mathrm{GSp}}_4 \times {\mathrm{GL}}_2$
. Furthermore, there is a remarkable identity, explained in more detail in §1.3, relating squares of (weighted averages of) fundamental Fourier coefficients and central values of dihedral twists of
![]() ${\mathrm{GSp}}_4$
and
${\mathrm{GSp}}_4$
and
![]() ${\mathrm{GL}}_2\ L$
-functions. Indeed, the fundamental Fourier coefficients are unipotent periods whose weighted averages are Bessel periods whose absolute squares are essentially central L-values of degree
${\mathrm{GL}}_2\ L$
-functions. Indeed, the fundamental Fourier coefficients are unipotent periods whose weighted averages are Bessel periods whose absolute squares are essentially central L-values of degree
![]() $8\ L$
-functions, via the refined Gan–Gross–Prasad conjectures [Reference Lester and Radziwiłł40].
$8\ L$
-functions, via the refined Gan–Gross–Prasad conjectures [Reference Lester and Radziwiłł40].
Motivated by these connections, the objective of this paper is to better understand the nature of the fundamental Fourier coefficients. In particular, we investigate the following questions:
-
• Are there many sign changes among the fundamental Fourier coefficients?
-
• How large (in the sense of both lower and upper bounds) are the fundamental Fourier coefficients?
We emphasize that while these kinds of questions have been previously studied for the full sequence
![]() $a(F,S)$
(
$a(F,S)$
(
![]() $S\in \Lambda _2$
) of Fourier coefficients attached to F (see [Reference Chandee12, Reference Gan and Takeda22, Reference Heath-Brown24] for results on sign changes and [Reference Das13] for an
$S\in \Lambda _2$
) of Fourier coefficients attached to F (see [Reference Chandee12, Reference Gan and Takeda22, Reference Heath-Brown24] for results on sign changes and [Reference Das13] for an
![]() $\Omega $
-result), there appears to be virtually no previous work in the more subtle setting where one restricts to fundamental Fourier coefficients. There has also been a fair bit of work on sign changes of Hecke eigenvalues of Siegel cusp forms [Reference Das and Kohnen14, Reference Kaczorowski and Perelli36, Reference Pitale and Schmidt45, Reference Royer, Sengupta and Wu53], which can be combined with the Hecke relations [Reference Atkin and Lehner1] to deduce sign changes among the
$\Omega $
-result), there appears to be virtually no previous work in the more subtle setting where one restricts to fundamental Fourier coefficients. There has also been a fair bit of work on sign changes of Hecke eigenvalues of Siegel cusp forms [Reference Das and Kohnen14, Reference Kaczorowski and Perelli36, Reference Pitale and Schmidt45, Reference Royer, Sengupta and Wu53], which can be combined with the Hecke relations [Reference Atkin and Lehner1] to deduce sign changes among the
![]() $a(F,S)$
with
$a(F,S)$
with
![]() ${\mathrm{disc}}(S)=dm^2$
, where d is a fixed fundamental discriminant and m varies. This should make it clear that the problem of obtaining sign changes or growth asymptotics for Fourier coefficients not associated to fundamental discriminants is of a different flavor (and relatively easier). Our focus in this paper is on the subsequence of Fourier coefficients
${\mathrm{disc}}(S)=dm^2$
, where d is a fixed fundamental discriminant and m varies. This should make it clear that the problem of obtaining sign changes or growth asymptotics for Fourier coefficients not associated to fundamental discriminants is of a different flavor (and relatively easier). Our focus in this paper is on the subsequence of Fourier coefficients
![]() $a(F,S)$
with S restricted to matrices of fundamental discriminant, where these questions are more difficult.
$a(F,S)$
with S restricted to matrices of fundamental discriminant, where these questions are more difficult.
1.1. Main results
Let
![]() $k> 2$
be an even integer and N be an odd square-free integer. Fix
$k> 2$
be an even integer and N be an odd square-free integer. Fix
 $F \in S_k(\Gamma _0^{(2)}(N))$
. If
$F \in S_k(\Gamma _0^{(2)}(N))$
. If
![]() $N>1$
, assume that F is an eigenform for the
$N>1$
, assume that F is an eigenform for the
![]() $U(p)$
Hecke operator (see equation (50)) for the finitely many primes
$U(p)$
Hecke operator (see equation (50)) for the finitely many primes
![]() $p\mid N$
; we make no assumptions concerning whether F is a Hecke eigenform at primes not dividing the level N. Our main result on sign changes is as follows:
$p\mid N$
; we make no assumptions concerning whether F is a Hecke eigenform at primes not dividing the level N. Our main result on sign changes is as follows:
Theorem A see Theorem 5.2
For F as before with real Fourier coefficients, one can fix M such that given
![]() $\varepsilon>0$
and sufficiently large X, there are
$\varepsilon>0$
and sufficiently large X, there are
![]() $ \ge X^{1-\varepsilon }$
distinct odd square-free integers
$ \ge X^{1-\varepsilon }$
distinct odd square-free integers
![]() $n_i \in [X, MX]$
and associated fundamental matrices
$n_i \in [X, MX]$
and associated fundamental matrices
![]() $S_i\in \Lambda _2$
with
$S_i\in \Lambda _2$
with
![]() $\lvert {\mathrm{disc}}(S_i)\rvert =n_i$
, such that with the
$\lvert {\mathrm{disc}}(S_i)\rvert =n_i$
, such that with the
![]() $n_i$
ordered in increasing manner, we have
$n_i$
ordered in increasing manner, we have
![]() $a(F, S_{i})a(F, S_{i+1})<0$
.
$a(F, S_{i})a(F, S_{i+1})<0$
.
Thus, Theorem A asserts that there are at least
![]() $X^{1-\varepsilon }$
(strict) sign changes among the fundamental Fourier coefficients of discriminant
$X^{1-\varepsilon }$
(strict) sign changes among the fundamental Fourier coefficients of discriminant
![]() $\asymp X$
. Interestingly, this also improves the exponent of the nonvanishing results of [Reference Saha56, Reference Schmidt58] mentioned earlier, where it was proved that there are
$\asymp X$
. Interestingly, this also improves the exponent of the nonvanishing results of [Reference Saha56, Reference Schmidt58] mentioned earlier, where it was proved that there are
![]() $\gg _\varepsilon X^{5/8 - \varepsilon }$
nonvanishing fundamental Fourier coefficients of discriminant up to X.
$\gg _\varepsilon X^{5/8 - \varepsilon }$
nonvanishing fundamental Fourier coefficients of discriminant up to X.
Another question left unanswered in all previous works is that of lower bounds for
![]() $\lvert a(F,S)\rvert $
with S fundamental. Let F be as before and fixed. A famous (and very deep) conjecture of Resnikoff and Saldana [Reference Roberts and Schmidt51] predicts that for S a fundamental matrixFootnote
2
in
$\lvert a(F,S)\rvert $
with S fundamental. Let F be as before and fixed. A famous (and very deep) conjecture of Resnikoff and Saldana [Reference Roberts and Schmidt51] predicts that for S a fundamental matrixFootnote
2
in
![]() $\Lambda _2$
,
$\Lambda _2$
,
 $$ \begin{align} \lvert a(F,S)\rvert \ll_{F,\varepsilon} \lvert{\mathrm{disc}}(S)\rvert^{\frac{k}2 -\frac{3}4 + \varepsilon}. \end{align} $$
$$ \begin{align} \lvert a(F,S)\rvert \ll_{F,\varepsilon} \lvert{\mathrm{disc}}(S)\rvert^{\frac{k}2 -\frac{3}4 + \varepsilon}. \end{align} $$
We prove a lower bound for many fundamental Fourier coefficients with an exponent of the same strength.
Theorem B see Theorem 5.3
For F as before,
![]() $\varepsilon>0$
fixed, and all sufficiently large X, there are
$\varepsilon>0$
fixed, and all sufficiently large X, there are
![]() $\ge X^{1-\varepsilon }$
distinct odd square-free integers
$\ge X^{1-\varepsilon }$
distinct odd square-free integers
![]() $n \in [X, 2X]$
, with associated fundamental matrices
$n \in [X, 2X]$
, with associated fundamental matrices
![]() $S_n$
such that
$S_n$
such that
![]() $\lvert {\mathrm{disc}}(S_n)\rvert =n$
and
$\lvert {\mathrm{disc}}(S_n)\rvert =n$
and
 $$ \begin{align*} \lvert a(F,S_n)\rvert \ge n^{\frac{k}2 - \frac34} \exp\left(\frac{1}{82} \sqrt{\frac{\log n}{\log \log n}} \right). \end{align*} $$
$$ \begin{align*} \lvert a(F,S_n)\rvert \ge n^{\frac{k}2 - \frac34} \exp\left(\frac{1}{82} \sqrt{\frac{\log n}{\log \log n}} \right). \end{align*} $$
Theorem B tells us that there are at least
![]() $X^{1-\varepsilon }$
fundamental Fourier coefficients of discriminant
$X^{1-\varepsilon }$
fundamental Fourier coefficients of discriminant
![]() $\asymp X$
whose sizes are ‘large’. Incidentally, just like Theorem A, Theorem B also improves upon the exponent of the set of nonvanishing fundamental coefficients obtained in [Reference Schmidt58] from
$\asymp X$
whose sizes are ‘large’. Incidentally, just like Theorem A, Theorem B also improves upon the exponent of the set of nonvanishing fundamental coefficients obtained in [Reference Schmidt58] from
![]() $5/8$
to
$5/8$
to
![]() $1$
.
$1$
.
Next, we investigate upper bounds for the Fourier coefficients
![]() $\lvert a(F,S)\rvert $
for fundamental S. The best currently known bound is due to Kohnen [Reference Kohnen35], who proved that
$\lvert a(F,S)\rvert $
for fundamental S. The best currently known bound is due to Kohnen [Reference Kohnen35], who proved that
 $\lvert a(F,S)\rvert \ll _{F, \varepsilon } \lvert {\mathrm{disc}}(S)\rvert ^{\frac {k}2 - \frac {13}{36}+\varepsilon }$
. This bound is quite far from the conjectured true bound (3). In fact, even if one were to assume the generalized Lindelöf hypothesis, one only obtains the upper bound
$\lvert a(F,S)\rvert \ll _{F, \varepsilon } \lvert {\mathrm{disc}}(S)\rvert ^{\frac {k}2 - \frac {13}{36}+\varepsilon }$
. This bound is quite far from the conjectured true bound (3). In fact, even if one were to assume the generalized Lindelöf hypothesis, one only obtains the upper bound
 $\ll _{F, \varepsilon }\lvert {\mathrm{disc}}(S)\rvert ^{\frac {k}2 - \frac {1}{2}+\varepsilon }$
(as explained later). Thus, the exponent
$\ll _{F, \varepsilon }\lvert {\mathrm{disc}}(S)\rvert ^{\frac {k}2 - \frac {1}{2}+\varepsilon }$
(as explained later). Thus, the exponent
 $\frac {k}2 - \frac {1}{2}$
appears to be a natural barrier. By using probabilistic methods and assuming the generalized Riemann hypothesis (GRH) for several L-functions, we are able to go beyond this barrier for the first time.
$\frac {k}2 - \frac {1}{2}$
appears to be a natural barrier. By using probabilistic methods and assuming the generalized Riemann hypothesis (GRH) for several L-functions, we are able to go beyond this barrier for the first time.
Theorem C see Theorem 5.14
Let
![]() $k> 2$
be an even integer and N be an odd square-free integer. Fix
$k> 2$
be an even integer and N be an odd square-free integer. Fix
 $F \in S_k(\Gamma _0^{(2)}(N))$
. Assume that the refined Gan–Gross–Prasad conjecture [Reference Lester and Radziwiłł40, equation (1.1)] holdsFootnote
3
for Bessel periods of holomorphic cusp forms on
$F \in S_k(\Gamma _0^{(2)}(N))$
. Assume that the refined Gan–Gross–Prasad conjecture [Reference Lester and Radziwiłł40, equation (1.1)] holdsFootnote
3
for Bessel periods of holomorphic cusp forms on
![]() ${\mathrm{SO}}_5({\mathbb A})$
. Assume that the GRH holds for L-functions in the Selberg class.Footnote
4
Then we have
${\mathrm{SO}}_5({\mathbb A})$
. Assume that the GRH holds for L-functions in the Selberg class.Footnote
4
Then we have
 $$ \begin{align*} \lvert a(F,S)\rvert \ll_{F, \varepsilon} \frac{\lvert{\mathrm{disc}}(S)\rvert^{\frac{k}2 - \frac{1}{2}}}{ \left(\log \lvert{\mathrm{disc}}(S)\rvert\right)^{\frac18 - \varepsilon}} \end{align*} $$
$$ \begin{align*} \lvert a(F,S)\rvert \ll_{F, \varepsilon} \frac{\lvert{\mathrm{disc}}(S)\rvert^{\frac{k}2 - \frac{1}{2}}}{ \left(\log \lvert{\mathrm{disc}}(S)\rvert\right)^{\frac18 - \varepsilon}} \end{align*} $$
for fundamental matrices S.
We note that a bound similar to that obtained in Theorem C has been recently proved in the special case where F is a Yoshida lift by Blomer and Brumley [Reference Böcherer and Das5, Corollary 4].
1.2. The reduction of Theorems A and B to half-integral-weight forms
The proofs of Theorems A and B rely on reducing these questions to corresponding ones about cusp forms of weight
 $k-\frac 12$
on the upper half-plane, exploiting the Fourier–Jacobi expansion of F and the relation between Jacobi forms and classical cusp forms of half-integral weight. More precisely, using [Reference Iwaniec28] it follows (see §5.2) that the set of primes p such that the pth Fourier–Jacobi coefficient of F is nonzero and has positive density in the set of all primes; fix any p in this set coprime to N. Using a classical construction going back to Eichler and Zagier [Reference Eichler and Zagier16, Theorem 5.6] in the case
$k-\frac 12$
on the upper half-plane, exploiting the Fourier–Jacobi expansion of F and the relation between Jacobi forms and classical cusp forms of half-integral weight. More precisely, using [Reference Iwaniec28] it follows (see §5.2) that the set of primes p such that the pth Fourier–Jacobi coefficient of F is nonzero and has positive density in the set of all primes; fix any p in this set coprime to N. Using a classical construction going back to Eichler and Zagier [Reference Eichler and Zagier16, Theorem 5.6] in the case
![]() $N=1$
and due to Manickam and Ramakrishnan [Reference Manickam and Ramakrishnan41] for square-free N, we can now construct a nonzero cusp form h of level
$N=1$
and due to Manickam and Ramakrishnan [Reference Manickam and Ramakrishnan41] for square-free N, we can now construct a nonzero cusp form h of level
![]() $4Np$
and weight
$4Np$
and weight
 $k-\frac 12$
whose Fourier coefficients
$k-\frac 12$
whose Fourier coefficients
![]() $a(h,n)$
essentially equal some
$a(h,n)$
essentially equal some
![]() $a(F,S)$
with
$a(F,S)$
with
![]() $\lvert {\mathrm{disc}}(S)\rvert =n$
.
$\lvert {\mathrm{disc}}(S)\rvert =n$
.
From this construction, Theorem A will follow if we can demonstrate
![]() $X^{1-\varepsilon }$
sign changes among the coefficients
$X^{1-\varepsilon }$
sign changes among the coefficients
![]() $a(h,n)$
of the half-integral-weight form h for odd square-free
$a(h,n)$
of the half-integral-weight form h for odd square-free
![]() $n\asymp X$
– which is exactly what we prove in Theorem 3.1, a result which builds upon works of Matomäki and Radziwiłł [Reference Lester and Radziwiłł39, Reference Matomäki and Radziwiłł42] and may be of independent interest. A point worth noting here is that h is not typically a Hecke eigenform (even when F is a Hecke eigenform), as the passage from Siegel cusp forms to Jacobi forms already described is not a functorial correspondence. The main ingredient for our proof of Theorem 3.1 is the demonstration of cancellation in sums of
$n\asymp X$
– which is exactly what we prove in Theorem 3.1, a result which builds upon works of Matomäki and Radziwiłł [Reference Lester and Radziwiłł39, Reference Matomäki and Radziwiłł42] and may be of independent interest. A point worth noting here is that h is not typically a Hecke eigenform (even when F is a Hecke eigenform), as the passage from Siegel cusp forms to Jacobi forms already described is not a functorial correspondence. The main ingredient for our proof of Theorem 3.1 is the demonstration of cancellation in sums of
![]() $a(h,n)$
over almost all short intervals, together with bounds on their moments, thereby providing a lower bound on sums of
$a(h,n)$
over almost all short intervals, together with bounds on their moments, thereby providing a lower bound on sums of
![]() $\lvert a(h,n)\rvert $
over almost all short intervals. Combining the two results shows that over many short intervals, the absolute value of the average of
$\lvert a(h,n)\rvert $
over almost all short intervals. Combining the two results shows that over many short intervals, the absolute value of the average of
![]() $a(h,n)$
is strictly smaller than that of
$a(h,n)$
is strictly smaller than that of
![]() $\lvert a(h,n)\rvert $
. Consequently, a sign change of
$\lvert a(h,n)\rvert $
. Consequently, a sign change of
![]() $a(h,n)$
occurs in many short intervals.
$a(h,n)$
occurs in many short intervals.
Likewise, Theorem B follows, provided we can demonstrate suitable large values for
![]() $\lvert a(h,n)\rvert $
. This is done in §4. The main result of that section, Theorem 4.1, says that there are at least
$\lvert a(h,n)\rvert $
. This is done in §4. The main result of that section, Theorem 4.1, says that there are at least
![]() $X^{1-\varepsilon }$
odd square-free
$X^{1-\varepsilon }$
odd square-free
![]() $n\asymp X$
with
$n\asymp X$
with
 $$ \begin{align*} \lvert a(h,n)\rvert \ge n^{\frac{k}2 - \frac34} \exp\left(\frac{1}{82} \sqrt{\frac{\log n}{\log \log n}} \right). \end{align*} $$
$$ \begin{align*} \lvert a(h,n)\rvert \ge n^{\frac{k}2 - \frac34} \exp\left(\frac{1}{82} \sqrt{\frac{\log n}{\log \log n}} \right). \end{align*} $$
Theorem 4.1 generalizes recent work of Gun, Kohnen, and Soundararajan [Reference Gun and Sengupta21] which dealt with the case of h of level
![]() $4$
. The proof of Theorem 4.1 follows the ‘resonance method’ strategy of [Reference Gun and Sengupta21, Reference Soundararajan63]; however, there are additional complications coming from the level which we need to overcome. The starting point of the proof is to use Kohnen’s basis for
$4$
. The proof of Theorem 4.1 follows the ‘resonance method’ strategy of [Reference Gun and Sengupta21, Reference Soundararajan63]; however, there are additional complications coming from the level which we need to overcome. The starting point of the proof is to use Kohnen’s basis for
 $S_{k+\frac 12}^+(4N)$
consisting of newforms and an explicit form of Waldspurger’s formula to reduce the problem to showing large values for (a weighted average of) a particular central L-value, while controlling the sizes of certain other central L-values (see Proposition 4.2 and the discussion after it, in particular estimates (31) and (32)). This is achieved by the resonance method as in [Reference Gun and Sengupta21]. A key technical input for this method is the evaluation of the first moment of twisted central L-values (Proposition 4.3), which is obtained following the method of [Reference Soundararajan and Young65]. Complications arising from the level show up here in the form of extra congruence and coprimality conditions, and these are dealt with as in [Reference Resnikoff and Saldana50].
$S_{k+\frac 12}^+(4N)$
consisting of newforms and an explicit form of Waldspurger’s formula to reduce the problem to showing large values for (a weighted average of) a particular central L-value, while controlling the sizes of certain other central L-values (see Proposition 4.2 and the discussion after it, in particular estimates (31) and (32)). This is achieved by the resonance method as in [Reference Gun and Sengupta21]. A key technical input for this method is the evaluation of the first moment of twisted central L-values (Proposition 4.3), which is obtained following the method of [Reference Soundararajan and Young65]. Complications arising from the level show up here in the form of extra congruence and coprimality conditions, and these are dealt with as in [Reference Resnikoff and Saldana50].
Theorem C, unlike Theorems A and B, does not involve a reduction to half-integral-weight forms. We further explain the main ideas behind its proof in §1.4.
Finally, we remark that a variant of the Fourier–Jacobi expansion trick sketched at the beginning of this subsection has been recently developed by Böcherer and Das to prove the nonvanishing of fundamental Fourier coefficients of Siegel modular forms of degree n [Reference Bump and Ginzburg7]. Using their variant, it seems plausible that the methods of this paper may allow one to extend Theorems A and B to Siegel cusp forms of higher degree. We do not pursue this extension here.
1.3. Central L-values for dihedral twists of spin L-functions
For two matrices
![]() $S_1, S_2$
in
$S_1, S_2$
in
![]() $\Lambda _2$
, write
$\Lambda _2$
, write
![]() $S_1 \sim S_2$
if there exists
$S_1 \sim S_2$
if there exists
![]() $A \in {\mathrm{SL}}_2({\mathbb Z})$
such that
$A \in {\mathrm{SL}}_2({\mathbb Z})$
such that
![]() $S_1 = {}^tA S_2A$
. Set
$S_1 = {}^tA S_2A$
. Set
 $F \in S_k(\Gamma _0^{(2)}(N))$
with
$F \in S_k(\Gamma _0^{(2)}(N))$
with
![]() $k>2$
even and N odd and square-free. Using the defining relation for Siegel cusp forms, we see that
$k>2$
even and N odd and square-free. Using the defining relation for Siegel cusp forms, we see that
thus showing that
![]() $a(F, S)$
depends only on the
$a(F, S)$
depends only on the
![]() ${\mathrm{SL}}_2({\mathbb Z})$
-equivalence class of the matrix S. Let
${\mathrm{SL}}_2({\mathbb Z})$
-equivalence class of the matrix S. Let
![]() $d < 0$
be a fundamental discriminant, let
$d < 0$
be a fundamental discriminant, let
![]() $\operatorname {\mathrm {Cl}}_K$
denote the ideal class group of
$\operatorname {\mathrm {Cl}}_K$
denote the ideal class group of
![]() $K= {\mathbb Q}(\sqrt {d})$
, and let
$K= {\mathbb Q}(\sqrt {d})$
, and let
![]() $w(K) \in \{2,4,6\}$
be the number of roots of unity in K. It is well known that the
$w(K) \in \{2,4,6\}$
be the number of roots of unity in K. It is well known that the
![]() ${\mathrm{SL}}_2({\mathbb Z})$
-equivalence classes of matrices in
${\mathrm{SL}}_2({\mathbb Z})$
-equivalence classes of matrices in
![]() $\Lambda _2$
of discriminant d are in natural bijective correspondence with the elements of
$\Lambda _2$
of discriminant d are in natural bijective correspondence with the elements of
![]() $\operatorname {\mathrm {Cl}}_K$
. So for any character
$\operatorname {\mathrm {Cl}}_K$
. So for any character
![]() $\Lambda $
of the finite group
$\Lambda $
of the finite group
![]() $\operatorname {\mathrm {Cl}}_K$
, we can define
$\operatorname {\mathrm {Cl}}_K$
, we can define
 $$ \begin{align} B(F, \Lambda) = \sum_{S \in \operatorname{\mathrm{Cl}}_K}a(F, S) \Lambda(S), \end{align} $$
$$ \begin{align} B(F, \Lambda) = \sum_{S \in \operatorname{\mathrm{Cl}}_K}a(F, S) \Lambda(S), \end{align} $$
which may be viewed as a Bessel period [Reference Dickson, Pitale, Saha and Schmidt15, Proposition 3.5].
The space
 $S_k(\Gamma _0^{(2)}(N))$
has a natural subspace
$S_k(\Gamma _0^{(2)}(N))$
has a natural subspace
 $S_k(\Gamma ^{(2)}_0(N))^{\mathrm{CAP}}$
spanned by the Saito–Kurokawa lifts. If F is a Saito–Kurokawa lift, then
$S_k(\Gamma ^{(2)}_0(N))^{\mathrm{CAP}}$
spanned by the Saito–Kurokawa lifts. If F is a Saito–Kurokawa lift, then
![]() $a(F,S)$
(for fundamental S) depends only on
$a(F,S)$
(for fundamental S) depends only on
![]() $d={\mathrm{disc}}(S)$
and is fairly well understood. In particular, for
$d={\mathrm{disc}}(S)$
and is fairly well understood. In particular, for
 $F \in S_k(\Gamma ^{(2)}_0(N))^{\mathrm{CAP}}$
, the Bessel period
$F \in S_k(\Gamma ^{(2)}_0(N))^{\mathrm{CAP}}$
, the Bessel period
![]() $B(F, \Lambda )$
vanishes whenever
$B(F, \Lambda )$
vanishes whenever
![]() $\Lambda \neq 1_K$
, where
$\Lambda \neq 1_K$
, where
![]() $1_K$
denotes the trivial character of
$1_K$
denotes the trivial character of
![]() $\operatorname {\mathrm {Cl}}_K$
. Now suppose that F is not a Saito–Kurokawa lift. Let
$\operatorname {\mathrm {Cl}}_K$
. Now suppose that F is not a Saito–Kurokawa lift. Let
![]() $\phi $
be the adelization of F, and suppose that
$\phi $
be the adelization of F, and suppose that
![]() $\phi $
generates an irreducible automorphic representation
$\phi $
generates an irreducible automorphic representation
![]() $\pi $
of
$\pi $
of
![]() ${\mathrm{GSp}}_4({\mathbb A})$
. Böcherer [Reference Berger, Dembélé, Pacetti and Şengün6] made the remarkable conjecture that
${\mathrm{GSp}}_4({\mathbb A})$
. Böcherer [Reference Berger, Dembélé, Pacetti and Şengün6] made the remarkable conjecture that
 $\lvert B(F, 1_K)\rvert ^2 = A_F \cdot w(K)^{2} \cdot \lvert d\rvert ^{k-1} \cdot L\left (\tfrac 12, \pi \otimes \chi _{d}\right )$
, where
$\lvert B(F, 1_K)\rvert ^2 = A_F \cdot w(K)^{2} \cdot \lvert d\rvert ^{k-1} \cdot L\left (\tfrac 12, \pi \otimes \chi _{d}\right )$
, where
![]() $\chi _d$
is the quadratic character associated to
$\chi _d$
is the quadratic character associated to
![]() $K/{\mathbb Q}$
and
$K/{\mathbb Q}$
and
![]() $A_F$
is a constant depending only on F.
$A_F$
is a constant depending only on F.
More generally, let
![]() ${\mathcal {AI}}(\Lambda )$
be the automorphic representation of
${\mathcal {AI}}(\Lambda )$
be the automorphic representation of
![]() ${\mathrm{GL}}(2,{\mathbb A})$
given by the automorphic induction of
${\mathrm{GL}}(2,{\mathbb A})$
given by the automorphic induction of
![]() $\Lambda $
from K; it is generated by (the adelization of) the dihedral modular form
$\Lambda $
from K; it is generated by (the adelization of) the dihedral modular form
 $\theta _{\Lambda }(z) = \sum _{0 \ne \mathfrak {a} \subset \mathcal O_K}\Lambda (\mathfrak {a}) e^{2 \pi i N(\mathfrak {a})z}$
of weight
$\theta _{\Lambda }(z) = \sum _{0 \ne \mathfrak {a} \subset \mathcal O_K}\Lambda (\mathfrak {a}) e^{2 \pi i N(\mathfrak {a})z}$
of weight
![]() $1$
. It is easy to check that
$1$
. It is easy to check that
![]() $L(s, \pi \otimes {\mathcal {AI}}(\Lambda )) = L(s, \pi ) L(s, \pi \otimes \chi _{d})$
. Now assume that the refined Gan–Gross–Prasad conjecture (see [Reference Dickson, Pitale, Saha and Schmidt15, Conjecture 1.12] and [Reference Lester and Radziwiłł40, (1.1)]) for the pair
$L(s, \pi \otimes {\mathcal {AI}}(\Lambda )) = L(s, \pi ) L(s, \pi \otimes \chi _{d})$
. Now assume that the refined Gan–Gross–Prasad conjecture (see [Reference Dickson, Pitale, Saha and Schmidt15, Conjecture 1.12] and [Reference Lester and Radziwiłł40, (1.1)]) for the pair
![]() $(\phi , \Lambda )$
holds true. In fact, this conjecture for
$(\phi , \Lambda )$
holds true. In fact, this conjecture for
![]() $\Lambda =1_K$
is now known, thanks to work of Furusawa and Morimoto [Reference Furusawa18] (which, combined with [Reference Dickson, Pitale, Saha and Schmidt15], completes the proof of Böcherer’s conjecture), who have also recently announced the proof for general
$\Lambda =1_K$
is now known, thanks to work of Furusawa and Morimoto [Reference Furusawa18] (which, combined with [Reference Dickson, Pitale, Saha and Schmidt15], completes the proof of Böcherer’s conjecture), who have also recently announced the proof for general
![]() $\Lambda $
. Then [Reference Dickson, Pitale, Saha and Schmidt15, Theorem 1.13] implies that under some mild assumptions,
$\Lambda $
. Then [Reference Dickson, Pitale, Saha and Schmidt15, Theorem 1.13] implies that under some mild assumptions,
 $$ \begin{align} \lvert B(F, \Lambda)\rvert^2 = c_F w(K)^2 \lvert d\rvert^{k-1}L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right), \end{align} $$
$$ \begin{align} \lvert B(F, \Lambda)\rvert^2 = c_F w(K)^2 \lvert d\rvert^{k-1}L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right), \end{align} $$
where
![]() $c_F$
is an explicit nonzero constant depending only on F and
$c_F$
is an explicit nonzero constant depending only on F and
![]() $L(s, \pi \times {\mathcal {AI}}(\Lambda ))$
is the tensor-product L-function of the spin (degree
$L(s, \pi \times {\mathcal {AI}}(\Lambda ))$
is the tensor-product L-function of the spin (degree
![]() $4$
) L-function of
$4$
) L-function of
![]() $\pi $
and the standard (degree
$\pi $
and the standard (degree
![]() $2$
) L-function of
$2$
) L-function of
![]() ${\mathcal {AI}}(\Lambda )$
. We show in Proposition 5.9 that a variant of equation (6) where the equality is replaced by an inequality holds in a more general setup (assuming the refined Gan–Gross–Prasad conjecture).
${\mathcal {AI}}(\Lambda )$
. We show in Proposition 5.9 that a variant of equation (6) where the equality is replaced by an inequality holds in a more general setup (assuming the refined Gan–Gross–Prasad conjecture).
The identities (5) and (6) demonstrate that the fundamental Fourier coefficients of Hecke eigenforms in
 $S_k(\Gamma _0^{(2)}(N))$
are intimately connected with central L-values of the degree
$S_k(\Gamma _0^{(2)}(N))$
are intimately connected with central L-values of the degree
![]() $8\ L$
-function
$8\ L$
-function
![]() $L(s, \pi \times {\mathcal {AI}}(\Lambda ))$
as
$L(s, \pi \times {\mathcal {AI}}(\Lambda ))$
as
![]() $\Lambda $
varies over the ideal class characters of K. By inverting equation (5), we can write
$\Lambda $
varies over the ideal class characters of K. By inverting equation (5), we can write
 $$ \begin{align} a(F,S) = \frac{1}{\lvert \operatorname{\mathrm{Cl}}_K\rvert}\sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} B(F, \Lambda) \Lambda^{-1}(S), \end{align} $$
$$ \begin{align} a(F,S) = \frac{1}{\lvert \operatorname{\mathrm{Cl}}_K\rvert}\sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} B(F, \Lambda) \Lambda^{-1}(S), \end{align} $$
which expresses each fundamental
![]() $a(F,S)$
as a weighted average of the Bessel periods
$a(F,S)$
as a weighted average of the Bessel periods
![]() $B(F, \Lambda )$
.
$B(F, \Lambda )$
.
Now, combining equations (6) and (7) with Theorem B, we obtain the following corollaries.
Corollary 1.1. Let
![]() $\pi $
be a cuspidal automorphic representation of
$\pi $
be a cuspidal automorphic representation of
![]() ${\mathrm{GSp}}_4({\mathbb A})$
that is not of Saito–Kurokawa type, such that
${\mathrm{GSp}}_4({\mathbb A})$
that is not of Saito–Kurokawa type, such that
![]() $\pi $
arises from a form in
$\pi $
arises from a form in
 $S_k(\Gamma _0^{(2)}(N))$
with
$S_k(\Gamma _0^{(2)}(N))$
with
![]() $k>2$
even and N odd and square-free. Fix
$k>2$
even and N odd and square-free. Fix
![]() $\varepsilon>0$
. Assume the refined Gan–Gross-Prasad conjecture [Reference Dickson, Pitale, Saha and Schmidt15, Conjecture 1.12]. Then for all sufficiently large X, there are
$\varepsilon>0$
. Assume the refined Gan–Gross-Prasad conjecture [Reference Dickson, Pitale, Saha and Schmidt15, Conjecture 1.12]. Then for all sufficiently large X, there are
![]() $\ge X^{1-\varepsilon }$
negative fundamental discriminants d with
$\ge X^{1-\varepsilon }$
negative fundamental discriminants d with
![]() $|d|\asymp X$
such that for
$|d|\asymp X$
such that for
![]() $K={\mathbb Q}(\sqrt {d})$
,
$K={\mathbb Q}(\sqrt {d})$
,
 $$ \begin{align*} \frac{1}{\lvert\operatorname{\mathrm{Cl}}_K\rvert}\sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right) \gg_\pi \lvert d\rvert^{-1/2} \exp\left(\frac{1}{82} \sqrt{\frac{\log \lvert d\rvert}{\log \log \lvert d\rvert}} \right). \end{align*} $$
$$ \begin{align*} \frac{1}{\lvert\operatorname{\mathrm{Cl}}_K\rvert}\sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right) \gg_\pi \lvert d\rvert^{-1/2} \exp\left(\frac{1}{82} \sqrt{\frac{\log \lvert d\rvert}{\log \log \lvert d\rvert}} \right). \end{align*} $$
By specializing further to the case of Yoshida lifts, we obtain the following application which is purely about central L-values of dihedral twists of classical newforms.
Corollary 1.2. Let
![]() $k>2$
be an even integer. Let
$k>2$
be an even integer. Let
![]() $N_1, N_2$
be two positive, square-free integers such that
$N_1, N_2$
be two positive, square-free integers such that
![]() $M = \gcd (N_1, N_2)>1$
. Let f be a holomorphic newform of weight
$M = \gcd (N_1, N_2)>1$
. Let f be a holomorphic newform of weight
![]() $2k-2$
on
$2k-2$
on
![]() $\Gamma _0(N_1)$
and g be a holomorphic newform of weight
$\Gamma _0(N_1)$
and g be a holomorphic newform of weight
![]() $2$
on
$2$
on
![]() $\Gamma _0(N_2)$
. Assume that for all primes p dividing M, the Atkin–Lehner eigenvalues of f and g coincide. Fix
$\Gamma _0(N_2)$
. Assume that for all primes p dividing M, the Atkin–Lehner eigenvalues of f and g coincide. Fix
![]() $\varepsilon>0$
. Then for all sufficiently large X, there are
$\varepsilon>0$
. Then for all sufficiently large X, there are
![]() $\ge X^{1-\varepsilon }$
negative fundamental discriminants d with
$\ge X^{1-\varepsilon }$
negative fundamental discriminants d with
![]() $\lvert d\rvert \asymp X$
with the property that there exists an ideal class group character
$\lvert d\rvert \asymp X$
with the property that there exists an ideal class group character
![]() $\Lambda $
of
$\Lambda $
of
![]() $K={\mathbb Q}(\sqrt {d})$
such that
$K={\mathbb Q}(\sqrt {d})$
such that
 $$ \begin{align*} L\left(\tfrac12, f \times {\mathcal{AI}}(\Lambda)\right) L\left(\tfrac12, g \times {\mathcal{AI}}(\Lambda)\right) \gg_{f,g} \lvert d\rvert^{-1/2} \exp\left(\frac{1}{82} \sqrt{\frac{\log \lvert d\rvert}{\log \log \lvert d\rvert}} \right). \end{align*} $$
$$ \begin{align*} L\left(\tfrac12, f \times {\mathcal{AI}}(\Lambda)\right) L\left(\tfrac12, g \times {\mathcal{AI}}(\Lambda)\right) \gg_{f,g} \lvert d\rvert^{-1/2} \exp\left(\frac{1}{82} \sqrt{\frac{\log \lvert d\rvert}{\log \log \lvert d\rvert}} \right). \end{align*} $$
Corollary 1.2 strengthens the main theorem of [Reference Schmidt58], which showed the existence of
![]() $\Lambda $
with (simultaneous) nonvanishing for
$\Lambda $
with (simultaneous) nonvanishing for
 $L\left (\frac 12, f \times {\mathcal {AI}}(\Lambda )\right )$
and
$L\left (\frac 12, f \times {\mathcal {AI}}(\Lambda )\right )$
and
 $L\left (\frac 12, g \times {\mathcal {AI}}(\Lambda )\right )$
and remarked, ‘While our method gives a lower bound on the number of non-vanishing twists, it does not give a lower bound on the size of the non-vanishing L-value itself’. Corollary 1.2 successfully achieves this.
$L\left (\frac 12, g \times {\mathcal {AI}}(\Lambda )\right )$
and remarked, ‘While our method gives a lower bound on the number of non-vanishing twists, it does not give a lower bound on the size of the non-vanishing L-value itself’. Corollary 1.2 successfully achieves this.
1.4. Fractional moments of L-values
Combining equations (6) and (7), we can write
 $$ \begin{align} \lvert a(F,S)\rvert \ll_F \lvert d\rvert^{\frac{k}{2}-\frac12}\frac{1}{\lvert\operatorname{\mathrm{Cl}}_K\rvert} \sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} \sqrt{L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right)}. \end{align} $$
$$ \begin{align} \lvert a(F,S)\rvert \ll_F \lvert d\rvert^{\frac{k}{2}-\frac12}\frac{1}{\lvert\operatorname{\mathrm{Cl}}_K\rvert} \sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} \sqrt{L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right)}. \end{align} $$
From the foregoing, we see that the generalized Lindelöf hypothesis for
 $L\left (\tfrac 12, \pi \times {\mathcal {AI}}(\Lambda )\right )$
implies that
$L\left (\tfrac 12, \pi \times {\mathcal {AI}}(\Lambda )\right )$
implies that
 $\lvert a(F,S)\rvert \ll _{F, \varepsilon } \lvert {\mathrm{disc}}(S)\rvert ^{\frac {k}2 - \frac {1}{2} + \varepsilon },$
which is still quite far from the bound (3).
$\lvert a(F,S)\rvert \ll _{F, \varepsilon } \lvert {\mathrm{disc}}(S)\rvert ^{\frac {k}2 - \frac {1}{2} + \varepsilon },$
which is still quite far from the bound (3).
Therefore, in order to prove Theorem C, we need to go beyond the bound obtained by a naive application of the generalized Lindelöf hypothesis. We do this by using Soundararajan’s method [Reference Saha and Schmidt64] for bounding moments of L-functions. Assuming the GRH, we prove the following bound (Theorem 6.1), which, thanks to the estimate (8), implies Theorem C:
 $$ \begin{align*} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{ \operatorname{Cl}_K}} \sqrt{L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right)} \ll_\varepsilon \frac{1}{(\log \lvert d\rvert)^{\frac18-\varepsilon}}. \end{align*} $$
$$ \begin{align*} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{ \operatorname{Cl}_K}} \sqrt{L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right)} \ll_\varepsilon \frac{1}{(\log \lvert d\rvert)^{\frac18-\varepsilon}}. \end{align*} $$
The main contribution to the moments of
 $L\left (\tfrac 12, \pi \times {\mathcal {AI}}(\Lambda )\right )$
will come from its large values, and we expect that these should be approximated by the large values of
$L\left (\tfrac 12, \pi \times {\mathcal {AI}}(\Lambda )\right )$
will come from its large values, and we expect that these should be approximated by the large values of
 $ \exp \left ( \sum _{p^n < \lvert d\rvert } \frac {b_{\pi \times {\mathcal {AI}}(\Lambda )}\left (p^n\right )}{ p^{n/2}}\right ), $
where
$ \exp \left ( \sum _{p^n < \lvert d\rvert } \frac {b_{\pi \times {\mathcal {AI}}(\Lambda )}\left (p^n\right )}{ p^{n/2}}\right ), $
where
![]() $b_{\pi \times {\mathcal {AI}}(\Lambda )}(n)$
is the nth coefficient of the Dirichlet series of
$b_{\pi \times {\mathcal {AI}}(\Lambda )}(n)$
is the nth coefficient of the Dirichlet series of
![]() $\log L(s,\pi \times {\mathcal {AI}}(\Lambda ))$
. For ease of discussion, let us assume here that d is prime,
$\log L(s,\pi \times {\mathcal {AI}}(\Lambda ))$
. For ease of discussion, let us assume here that d is prime,
![]() $N=1$
, and
$N=1$
, and
![]() $\pi $
transfers to a cuspidal representation of
$\pi $
transfers to a cuspidal representation of
![]() ${\mathrm{GL}}_4$
.Footnote
5
Separately analyzing the primes, squares of primes, and higher prime powers, we show under GRH that
${\mathrm{GL}}_4$
.Footnote
5
Separately analyzing the primes, squares of primes, and higher prime powers, we show under GRH that
 $$ \begin{align*} \sum_{p^n < \lvert d\rvert} \frac{b_{\pi \times {\mathcal{AI}}(\Lambda)}\left(p^n\right)}{ p^{n/2}}= \sum_{p < \lvert d\rvert} \frac{b_{\pi}(p)b_{{\mathcal{AI}}(\Lambda)}(p)}{\sqrt{p}}-\frac{1}{2} \log \log \lvert d\rvert(1+o(1)), \end{align*} $$
$$ \begin{align*} \sum_{p^n < \lvert d\rvert} \frac{b_{\pi \times {\mathcal{AI}}(\Lambda)}\left(p^n\right)}{ p^{n/2}}= \sum_{p < \lvert d\rvert} \frac{b_{\pi}(p)b_{{\mathcal{AI}}(\Lambda)}(p)}{\sqrt{p}}-\frac{1}{2} \log \log \lvert d\rvert(1+o(1)), \end{align*} $$
where
![]() $b_{\pi }(p)$
and
$b_{\pi }(p)$
and
![]() $b_{{\mathcal {AI}}(\Lambda )}(p)$
respectively denote the pth coefficients of the Dirichlet series of
$b_{{\mathcal {AI}}(\Lambda )}(p)$
respectively denote the pth coefficients of the Dirichlet series of
![]() $\log L(s,\pi )$
and of
$\log L(s,\pi )$
and of
![]() $ \log L(s, {\mathcal {AI}}(\Lambda ))$
. For primes with
$ \log L(s, {\mathcal {AI}}(\Lambda ))$
. For primes with
 $\left (\frac {d}{p}\right )=1$
so that
$\left (\frac {d}{p}\right )=1$
so that
![]() $p\mathcal O_K=\mathfrak p \overline {\mathfrak p}$
, as
$p\mathcal O_K=\mathfrak p \overline {\mathfrak p}$
, as
![]() $\Lambda $
varies over
$\Lambda $
varies over
![]() $\widehat {\operatorname {Cl}_K}$
, we expect that
$\widehat {\operatorname {Cl}_K}$
, we expect that
 $b_{{\mathcal {AI}}(\Lambda )}(p)=\Lambda (\mathfrak p)+\Lambda (\mathfrak p)^{-1}$
behaves like the random variable
$b_{{\mathcal {AI}}(\Lambda )}(p)=\Lambda (\mathfrak p)+\Lambda (\mathfrak p)^{-1}$
behaves like the random variable
 $X_p+X_p^{-1}$
, where
$X_p+X_p^{-1}$
, where
 $\left \{X_p\right \}_p$
are independent and identically distributed random variables uniformly distributed on the unit circle – if
$\left \{X_p\right \}_p$
are independent and identically distributed random variables uniformly distributed on the unit circle – if
 $\left (\frac {d}{p}\right )=-1$
,
$\left (\frac {d}{p}\right )=-1$
,
![]() $b_{{\mathcal {AI}}(\Lambda )}(p)=0$
. Consequently, the sum on the right-hand side in the foregoing equation is modeled by the random variable
$b_{{\mathcal {AI}}(\Lambda )}(p)=0$
. Consequently, the sum on the right-hand side in the foregoing equation is modeled by the random variable
 $\sum _{p < \lvert d\rvert } \frac {b_{\pi }(p) \left (X_p+X_p^{-1}\right )}{\sqrt {p}} 1_{\left (\frac {d}{p}\right )=1}$
, which can be shown to have a normal limiting distribution as
$\sum _{p < \lvert d\rvert } \frac {b_{\pi }(p) \left (X_p+X_p^{-1}\right )}{\sqrt {p}} 1_{\left (\frac {d}{p}\right )=1}$
, which can be shown to have a normal limiting distribution as
![]() $d \rightarrow \infty $
with mean
$d \rightarrow \infty $
with mean
![]() $0$
and variance
$0$
and variance
 $2\sum _{\substack {p < \lvert d\rvert }} \frac {b_{\pi }(p)^2 }{p} 1_{\left (\frac {d}{p}\right )=1} \sim \log \log \lvert d\rvert $
, which we prove under the GRH. The preceding discussion suggests
$2\sum _{\substack {p < \lvert d\rvert }} \frac {b_{\pi }(p)^2 }{p} 1_{\left (\frac {d}{p}\right )=1} \sim \log \log \lvert d\rvert $
, which we prove under the GRH. The preceding discussion suggests
 $$ \begin{align*} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{ \operatorname{Cl}_K}} \sqrt{L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right)} & \asymp (\log \lvert d\rvert)^{-1/4} \mathbb E \!\left(\! \exp \!\left(\! \frac{1}{2} \sum_{p < \lvert d\rvert} \frac{b_{\pi}(p) \!\left(X_p+X_p^{-1} \!\right)\! 1_{ \!\left( \!\frac{d}{p}\right)=1}}{\sqrt{p}} \!\right)\!\right) \\ & \asymp (\log \lvert d\rvert)^{-1/8}, \end{align*} $$
$$ \begin{align*} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{ \operatorname{Cl}_K}} \sqrt{L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right)} & \asymp (\log \lvert d\rvert)^{-1/4} \mathbb E \!\left(\! \exp \!\left(\! \frac{1}{2} \sum_{p < \lvert d\rvert} \frac{b_{\pi}(p) \!\left(X_p+X_p^{-1} \!\right)\! 1_{ \!\left( \!\frac{d}{p}\right)=1}}{\sqrt{p}} \!\right)\!\right) \\ & \asymp (\log \lvert d\rvert)^{-1/8}, \end{align*} $$
where in the last step we have used the fact that the moment-generating function of a normal random variable X with mean
![]() $0$
and variance
$0$
and variance
![]() $\sigma ^2$
is given by
$\sigma ^2$
is given by
 $\mathbb E \left (e^{zX}\right )=e^{\frac 12 z^2 \sigma ^2}$
. Remarkably, Soundararajan’s method allows us to make this heuristic argument rigorous for the upper bound, up to the loss of a factor
$\mathbb E \left (e^{zX}\right )=e^{\frac 12 z^2 \sigma ^2}$
. Remarkably, Soundararajan’s method allows us to make this heuristic argument rigorous for the upper bound, up to the loss of a factor
![]() $(\log \lvert d\rvert )^{\varepsilon }$
, which occurs due to a suboptimal treatment of the large primes.
$(\log \lvert d\rvert )^{\varepsilon }$
, which occurs due to a suboptimal treatment of the large primes.
1.5. Notations
We use the notation
![]() $A \ll _{x,y,z} B$
to signify that there exists a positive constant C, depending at most upon
$A \ll _{x,y,z} B$
to signify that there exists a positive constant C, depending at most upon
![]() $x,y,z$
, such that
$x,y,z$
, such that
![]() $\lvert A\rvert \leq C \lvert B\rvert $
. The symbol
$\lvert A\rvert \leq C \lvert B\rvert $
. The symbol
![]() $\varepsilon $
will denote a small positive quantity. We write
$\varepsilon $
will denote a small positive quantity. We write
![]() $A(x) = O_y(B(x))$
if there exists a positive real number M (depending on y) and a real number
$A(x) = O_y(B(x))$
if there exists a positive real number M (depending on y) and a real number
![]() $x_0$
such that
$x_0$
such that
![]() $\lvert A(x)\rvert \le M \lvert B(x)\rvert $
for all
$\lvert A(x)\rvert \le M \lvert B(x)\rvert $
for all
![]() $x \ge x_0$
.
$x \ge x_0$
.
For a positive integer n with prime factorization
 $n = \prod _{i=1}^k p_i^{\alpha _i}$
, we define
$n = \prod _{i=1}^k p_i^{\alpha _i}$
, we define
![]() $\omega (n)=k$
,
$\omega (n)=k$
,
 $\Omega (n)=\sum _{i=1}^k \alpha _i$
. We let
$\Omega (n)=\sum _{i=1}^k \alpha _i$
. We let
![]() $\mu (n)$
denote the Möbius function – that is,
$\mu (n)$
denote the Möbius function – that is,
![]() $\mu (n)=(-1)^{\omega (n)}$
if
$\mu (n)=(-1)^{\omega (n)}$
if
![]() $\omega (n)=\Omega (n)$
, and
$\omega (n)=\Omega (n)$
, and
![]() $\mu (n) =0$
otherwise. We say that n is square-free if
$\mu (n) =0$
otherwise. We say that n is square-free if
![]() $\mu (n) \neq 0$
. We let
$\mu (n) \neq 0$
. We let
![]() $(a,b)$
or
$(a,b)$
or
![]() $\gcd (a,b)$
denote the greatest common divisor of a and b.
$\gcd (a,b)$
denote the greatest common divisor of a and b.
We say that d is a fundamental discriminant if d is the discriminant of the field
![]() ${\mathbb Q}(\sqrt {d})$
. For a fundamental discriminant d, we let
${\mathbb Q}(\sqrt {d})$
. For a fundamental discriminant d, we let
![]() $\chi _d$
be the associated quadratic Dirichlet character. Given any representation
$\chi _d$
be the associated quadratic Dirichlet character. Given any representation
![]() $\pi $
of a group, we let
$\pi $
of a group, we let
![]() $\hat {\pi }$
denote the contragredient and
$\hat {\pi }$
denote the contragredient and
![]() $V_\pi $
denote the representation space. We use
$V_\pi $
denote the representation space. We use
![]() ${\mathbb A}$
to denote the ring of adeles over
${\mathbb A}$
to denote the ring of adeles over
![]() ${\mathbb Q}$
and we use
${\mathbb Q}$
and we use
![]() ${\mathbb A}_F$
to denote the ring of adeles over F for a general number field F. If G is a reductive group such that the local Langlands correspondence is known for each
${\mathbb A}_F$
to denote the ring of adeles over F for a general number field F. If G is a reductive group such that the local Langlands correspondence is known for each
![]() $G(F_v)$
and
$G(F_v)$
and
![]() $\pi $
is an automorphic representation of
$\pi $
is an automorphic representation of
![]() $G({\mathbb A}_F)$
, then we formally (as an Euler product over finite places) define the L-function
$G({\mathbb A}_F)$
, then we formally (as an Euler product over finite places) define the L-function
![]() $L(s, \rho (\pi )):= L(s, \pi , \rho )$
for each finite-dimensional representation
$L(s, \rho (\pi )):= L(s, \pi , \rho )$
for each finite-dimensional representation
![]() $\rho $
of the dual group. All L-functions in this paper will denote the finite part of the L-function (i.e., without the Archimedean factors), so that for a number field F and an automorphic representation
$\rho $
of the dual group. All L-functions in this paper will denote the finite part of the L-function (i.e., without the Archimedean factors), so that for a number field F and an automorphic representation
![]() $\pi $
of
$\pi $
of
![]() ${\mathrm{GL}}_n(F)$
, we have
${\mathrm{GL}}_n(F)$
, we have
![]() $L(s, \pi ) = \prod _{v<\infty } L(s, \pi _v)$
. All L-functions will be normalized to take
$L(s, \pi ) = \prod _{v<\infty } L(s, \pi _v)$
. All L-functions will be normalized to take
![]() $s \mapsto 1-s$
. For an integer N we denote
$s \mapsto 1-s$
. For an integer N we denote
 $L^N(s, \pi )=\prod _{v \nmid N}L(s, \pi _v)$
. Given a reductive group G and two irreducible automorphic representations
$L^N(s, \pi )=\prod _{v \nmid N}L(s, \pi _v)$
. Given a reductive group G and two irreducible automorphic representations
![]() $\pi = \otimes _v \pi _v$
and
$\pi = \otimes _v \pi _v$
and
![]() $\sigma = \otimes _v \sigma _v$
of
$\sigma = \otimes _v \sigma _v$
of
![]() $G({\mathbb A}_F)$
, we say that
$G({\mathbb A}_F)$
, we say that
![]() $\pi $
and
$\pi $
and
![]() $\sigma $
are nearly equivalent if
$\sigma $
are nearly equivalent if
![]() $\pi _v \simeq \sigma _v$
for all but finite many places v of F.
$\pi _v \simeq \sigma _v$
for all but finite many places v of F.
2. Preliminaries on half-integral-weight forms
The goal of this section is to set up some notation and lay out some key properties concerning cusp forms of half-integral weight on the complex upper half-plane.
2.1. Notation
The group
![]() ${\mathrm{SL}}_2({\mathbb R})$
acts on the upper half-plane
${\mathrm{SL}}_2({\mathbb R})$
acts on the upper half-plane
![]() $\mathbb H$
by
$\mathbb H$
by
 $\gamma z = \frac {az+b}{cz+d}$
, where
$\gamma z = \frac {az+b}{cz+d}$
, where
 $\gamma = {\left (\begin {array}{@{}cc@{}}a&b\\c&d\end {array}\right )} $
and
$\gamma = {\left (\begin {array}{@{}cc@{}}a&b\\c&d\end {array}\right )} $
and
![]() $z=x+iy $
. For a positive integer N, let
$z=x+iy $
. For a positive integer N, let
![]() $\Gamma _0(N)$
denote the congruence subgroup consisting of matrices
$\Gamma _0(N)$
denote the congruence subgroup consisting of matrices
 ${\left (\begin {array}{@{}cc@{}}a&b\\c&d\end {array}\right )}$
in
${\left (\begin {array}{@{}cc@{}}a&b\\c&d\end {array}\right )}$
in
![]() ${\mathrm{SL}}_2({\mathbb Z})$
such that N divides c. For a complex number z, let
${\mathrm{SL}}_2({\mathbb Z})$
such that N divides c. For a complex number z, let
![]() $e(z)$
denote
$e(z)$
denote
![]() $e^{2\pi i z}$
.
$e^{2\pi i z}$
.
Let
 $\theta (z) = \sum _{n = -\infty }^\infty e\left (n^2 z\right )$
be the standard theta function on
$\theta (z) = \sum _{n = -\infty }^\infty e\left (n^2 z\right )$
be the standard theta function on
![]() $\mathbb H$
. If
$\mathbb H$
. If
 $A = {\left (\begin {array}{@{}cc@{}}a&b\\c&d\end {array}\right )} \in \Gamma _0(4)$
, we have
$A = {\left (\begin {array}{@{}cc@{}}a&b\\c&d\end {array}\right )} \in \Gamma _0(4)$
, we have
![]() $\theta (Az) = j(A, z)\theta (z)$
, where
$\theta (Az) = j(A, z)\theta (z)$
, where
![]() $j(A, z)$
is the so-called
$j(A, z)$
is the so-called
![]() $\theta $
-multiplier. For an explicit formula for
$\theta $
-multiplier. For an explicit formula for
![]() $j(A, z)$
, see [Reference Soundararajan62, (1.10)]. Let
$j(A, z)$
, see [Reference Soundararajan62, (1.10)]. Let
 $S_{k+\frac {1}{2}}(4N)$
denote the space of holomorphic cusp forms of weight
$S_{k+\frac {1}{2}}(4N)$
denote the space of holomorphic cusp forms of weight
 $k+\frac {1}{2}$
for the group
$k+\frac {1}{2}$
for the group
![]() $\Gamma _0(4N)$
. In other words, a function
$\Gamma _0(4N)$
. In other words, a function
![]() $f : \mathbb H \rightarrow {\mathbb C}$
belongs to
$f : \mathbb H \rightarrow {\mathbb C}$
belongs to
 $S_{k+\frac {1}{2}}(4N)$
if
$S_{k+\frac {1}{2}}(4N)$
if
-
i)
 $f(Az) = j(A, z)^{2k +1} f(z)$
for every
$f(Az) = j(A, z)^{2k +1} f(z)$
for every
 $A = {\left (\begin {array}{@{}cc@{}}a&b\\c&d\end {array}\right )} \in \Gamma _0(4N)$
,
$A = {\left (\begin {array}{@{}cc@{}}a&b\\c&d\end {array}\right )} \in \Gamma _0(4N)$
, -
ii) f is holomorphic,
-
iii) and f vanishes at the cusps.
Any
 $f \in S_{k+\frac {1}{2}}(4N)$
has the Fourier expansion
$f \in S_{k+\frac {1}{2}}(4N)$
has the Fourier expansion
 $$ \begin{align*} f(z) = \sum_{n> 0} a(f, n)e(nz). \end{align*} $$
$$ \begin{align*} f(z) = \sum_{n> 0} a(f, n)e(nz). \end{align*} $$
We let
![]() $c(f,n)$
denote the ‘normalized’ Fourier coefficients, defined by
$c(f,n)$
denote the ‘normalized’ Fourier coefficients, defined by
 $$ \begin{align*} c(f,n) = a(f,n)n^{ \frac14-\frac k2}. \end{align*} $$
$$ \begin{align*} c(f,n) = a(f,n)n^{ \frac14-\frac k2}. \end{align*} $$
For
 $f, g \in S_{k+\frac 12}(4N)$
, we define the Petersson inner product
$f, g \in S_{k+\frac 12}(4N)$
, we define the Petersson inner product
![]() $\langle f, g\rangle $
by
$\langle f, g\rangle $
by
 $$ \begin{align*} \langle f, g\rangle = [{\textrm{SL}}_2({\mathbb Z}): \Gamma_0(4N)]^{-1} \int_{\Gamma_0(N) \backslash \mathbb H}f(z) \overline{g(z)} y^{k + \frac12} \frac{dx dy}{y^2}. \end{align*} $$
$$ \begin{align*} \langle f, g\rangle = [{\textrm{SL}}_2({\mathbb Z}): \Gamma_0(4N)]^{-1} \int_{\Gamma_0(N) \backslash \mathbb H}f(z) \overline{g(z)} y^{k + \frac12} \frac{dx dy}{y^2}. \end{align*} $$
2.2. The Kohnen plus space and decomposition into old and newspaces
Fix positive integers
![]() $k, N$
such that N is odd and square-free. We recall the definition of the Kohnen plus space
$k, N$
such that N is odd and square-free. We recall the definition of the Kohnen plus space
 $S^+_{k+\frac 12}(4N) \subseteq S_{k+\frac 12}(4N).$
The space
$S^+_{k+\frac 12}(4N) \subseteq S_{k+\frac 12}(4N).$
The space
 $S^+_{k+\frac 12}(4N)$
consists of all forms f in
$S^+_{k+\frac 12}(4N)$
consists of all forms f in
 $S_{k+\frac 12}(4N)$
for which
$S_{k+\frac 12}(4N)$
for which
![]() $a(f,n) = 0$
whenever
$a(f,n) = 0$
whenever
![]() $n \equiv (-1)^{k+1}$
or
$n \equiv (-1)^{k+1}$
or
![]() $2 \bmod {4}$
. According to the results of [Reference Kohnen33], there exists a canonically defined subspace
$2 \bmod {4}$
. According to the results of [Reference Kohnen33], there exists a canonically defined subspace
 $S^{+, \mathrm {new}}_{k+\frac 12}(4N) \subset S^+_{k+\frac 12}(4N)$
and a decomposition
$S^{+, \mathrm {new}}_{k+\frac 12}(4N) \subset S^+_{k+\frac 12}(4N)$
and a decomposition
 $$ \begin{align} S^+_{k+\frac12}(4N) = \bigoplus_{\substack{r, \ell \ge 1 \\ r \ell\mid N}} S^{+, \mathrm{new}}_{k+\frac12}(4\ell)\mid U\left(r^2\right), \end{align} $$
$$ \begin{align} S^+_{k+\frac12}(4N) = \bigoplus_{\substack{r, \ell \ge 1 \\ r \ell\mid N}} S^{+, \mathrm{new}}_{k+\frac12}(4\ell)\mid U\left(r^2\right), \end{align} $$
where we define
 $$ \begin{align} f\mid U\left(r^2\right) = r^{\frac12 - k}\sum_{n>0 }a\left(f,r^2n\right)e(nz). \end{align} $$
$$ \begin{align} f\mid U\left(r^2\right) = r^{\frac12 - k}\sum_{n>0 }a\left(f,r^2n\right)e(nz). \end{align} $$
It is known [Reference Soundararajan62, Proposition 1.5] that if
![]() $(r, \ell )=1$
, then
$(r, \ell )=1$
, then
 $U\left (r^2\right )$
takes
$U\left (r^2\right )$
takes
 $S_{k + \frac 12}(4\ell )$
to
$S_{k + \frac 12}(4\ell )$
to
 $S_{k + \frac 12}(4r\ell )$
. It is also useful to note that
$S_{k + \frac 12}(4r\ell )$
. It is also useful to note that
 $$ \begin{align} c\left(f\mid U\left(r^2\right), n\right) = c\left(f, r^2 n\right). \end{align} $$
$$ \begin{align} c\left(f\mid U\left(r^2\right), n\right) = c\left(f, r^2 n\right). \end{align} $$
2.3. Hecke operators and the Shimura correspondence
For all primes p coprime to N there exist Hecke operators
 $T\left (p^2\right )$
acting on the space
$T\left (p^2\right )$
acting on the space
 $S_{k+\frac 12}(4N)$
(see [Reference Soundararajan62, Theorem 1.7]). A newform in
$S_{k+\frac 12}(4N)$
(see [Reference Soundararajan62, Theorem 1.7]). A newform in
 $S^{+, \mathrm {new}}_{k+\frac 12}(4N)$
is defined to be an element of
$S^{+, \mathrm {new}}_{k+\frac 12}(4N)$
is defined to be an element of
 $S^{+, \mathrm {new}}_{k+\frac 12}(4N)$
that is an eigenfunction of the Hecke operators
$S^{+, \mathrm {new}}_{k+\frac 12}(4N)$
that is an eigenfunction of the Hecke operators
 $T\left (p^2\right )$
for
$T\left (p^2\right )$
for
![]() $p\nmid N$
. The newforms are uniquely determined up to multiplication by nonzero complex numbers and are in fact also eigenforms for the operators
$p\nmid N$
. The newforms are uniquely determined up to multiplication by nonzero complex numbers and are in fact also eigenforms for the operators
 $U\left (p^2\right )$
for all
$U\left (p^2\right )$
for all
![]() $p\mid N$
[Reference Kohnen33, Theorem 2]. The space
$p\mid N$
[Reference Kohnen33, Theorem 2]. The space
 $S^{+, \mathrm {new}}_{k+\frac 12}(4N)$
has an orthogonal basis consisting of newforms.
$S^{+, \mathrm {new}}_{k+\frac 12}(4N)$
has an orthogonal basis consisting of newforms.
According to the Shimura lifting [Reference Soundararajan62] as refined by Kohnen in [Reference Kohnen33], there is an isomorphism
 $$ \begin{align} S^{+, \mathrm{new}}_{k+\frac12}(4N) \overset{\simeq}{\rightarrow} S_{2k}^{\mathrm{new}}(N) \end{align} $$
$$ \begin{align} S^{+, \mathrm{new}}_{k+\frac12}(4N) \overset{\simeq}{\rightarrow} S_{2k}^{\mathrm{new}}(N) \end{align} $$
as Hecke modules, where
![]() $S_{2k}^{\mathrm {new}}(N)$
is the orthogonal complement of the space of cuspidal oldforms of weight
$S_{2k}^{\mathrm {new}}(N)$
is the orthogonal complement of the space of cuspidal oldforms of weight
![]() $2k$
for
$2k$
for
![]() $\Gamma _0(N)$
as defined by Atkin and Lehner [Reference Arthur3]. The Shimura lifting takes each newform in
$\Gamma _0(N)$
as defined by Atkin and Lehner [Reference Arthur3]. The Shimura lifting takes each newform in
 $S^{+, \mathrm {new}}_{k+\frac 12}(4N)$
(as already defined) to a newform (in the sense of Atkin and Lehner [Reference Arthur3, Lemma 18]) in
$S^{+, \mathrm {new}}_{k+\frac 12}(4N)$
(as already defined) to a newform (in the sense of Atkin and Lehner [Reference Arthur3, Lemma 18]) in
![]() $S_{2k}^{\mathrm {new}}(N)$
with the same Hecke eigenvalues. More precisely, if
$S_{2k}^{\mathrm {new}}(N)$
with the same Hecke eigenvalues. More precisely, if
 $f \in S^{+, \mathrm {new}}_{k+\frac 12}(4N)$
is a newform and
$f \in S^{+, \mathrm {new}}_{k+\frac 12}(4N)$
is a newform and
![]() $g \in S_{2k}^{\mathrm {new}}(N)$
is the Shimura lift of f according to isomorphism (12), then for each prime
$g \in S_{2k}^{\mathrm {new}}(N)$
is the Shimura lift of f according to isomorphism (12), then for each prime
![]() $p \nmid N$
there exists a real number
$p \nmid N$
there exists a real number
![]() $\lambda _f(p) \in [-2, 2]$
(by Deligne’s bound for the normalized Hecke eigenvalue) such that
$\lambda _f(p) \in [-2, 2]$
(by Deligne’s bound for the normalized Hecke eigenvalue) such that
 $$ \begin{align*} f\mid T\left(p^2\right) = \lambda_f(p) p^{k - \frac12} f, \qquad g\mid T(p) = \lambda_f(p) p^{k - \frac12} g. \end{align*} $$
$$ \begin{align*} f\mid T\left(p^2\right) = \lambda_f(p) p^{k - \frac12} f, \qquad g\mid T(p) = \lambda_f(p) p^{k - \frac12} g. \end{align*} $$
In view of decomposition (9) and the fact that the operators
![]() $U(p)$
with
$U(p)$
with
![]() $p\mid N$
commute with
$p\mid N$
commute with
 $T\left (p^2\right )$
,
$T\left (p^2\right )$
,
![]() $p \nmid N$
, a basis of
$p \nmid N$
, a basis of
 $S^{+}_{k+\frac 12}(4N)$
consisting of eigenforms for
$S^{+}_{k+\frac 12}(4N)$
consisting of eigenforms for
 $T\left (p^2\right )$
,
$T\left (p^2\right )$
,
![]() $p\nmid N$
, is given by
$p\nmid N$
, is given by
 $$ \begin{align} {\mathcal B}_{k+\frac12,4N} = \bigcup_{\substack{r, \ell \ge 1 \\ r \ell\mid N}} \left\{f\mid U\left(r^2\right): f\in {\mathcal B}^{\mathrm{new}}_{k+\frac12,4\ell}\right\}, \end{align} $$
$$ \begin{align} {\mathcal B}_{k+\frac12,4N} = \bigcup_{\substack{r, \ell \ge 1 \\ r \ell\mid N}} \left\{f\mid U\left(r^2\right): f\in {\mathcal B}^{\mathrm{new}}_{k+\frac12,4\ell}\right\}, \end{align} $$
where
 ${\mathcal B}^{\mathrm {new}}_{k+\frac 12,4\ell }$
is an orthogonal basis of
${\mathcal B}^{\mathrm {new}}_{k+\frac 12,4\ell }$
is an orthogonal basis of
 $S^{+, \mathrm {new}}_{k+\frac 12}(4\ell )$
consisting of newforms. Note, however, that it is not necessarily the case that all members of
$S^{+, \mathrm {new}}_{k+\frac 12}(4\ell )$
consisting of newforms. Note, however, that it is not necessarily the case that all members of
 ${\mathcal B}_{k+\frac 12,4N}$
are orthogonal to each other. The following result will be useful for us; recall the definitions of
${\mathcal B}_{k+\frac 12,4N}$
are orthogonal to each other. The following result will be useful for us; recall the definitions of
![]() $\Omega (n)$
and
$\Omega (n)$
and
![]() $\omega (n)$
from §1.5:
$\omega (n)$
from §1.5:
Lemma 2.1. Let
![]() $r, \ell $
be positive, odd, square-free integers with
$r, \ell $
be positive, odd, square-free integers with
![]() $(r, \ell )=1$
and let
$(r, \ell )=1$
and let
 $f \in S^{+, \mathrm {new}}_{k+\frac 12}(4\ell )$
be a newform. Then for any odd square-free integer n, putting
$f \in S^{+, \mathrm {new}}_{k+\frac 12}(4\ell )$
be a newform. Then for any odd square-free integer n, putting
![]() $d=(-1)^kn$
, we have
$d=(-1)^kn$
, we have
 $$ \begin{align*} c\left(f\mid U\left(r^2\right), n\right) = c\left(f, r^2n\right) = c(f,n) \prod_{p\mid r}\left(\lambda_f(p) - \frac{1}{\sqrt{p}}\left(\frac{d}{p} \right) \right). \end{align*} $$
$$ \begin{align*} c\left(f\mid U\left(r^2\right), n\right) = c\left(f, r^2n\right) = c(f,n) \prod_{p\mid r}\left(\lambda_f(p) - \frac{1}{\sqrt{p}}\left(\frac{d}{p} \right) \right). \end{align*} $$
Additionally, for any odd integer
![]() $r \ge 1$
with
$r \ge 1$
with
![]() $(r,\ell )=1$
, we have
$(r,\ell )=1$
, we have
 $$ \begin{align*} \left\lvert c\left(f,r^2n\right)\right\rvert \le 3^{\Omega(r)} \lvert c(f,n)\rvert. \end{align*} $$
$$ \begin{align*} \left\lvert c\left(f,r^2n\right)\right\rvert \le 3^{\Omega(r)} \lvert c(f,n)\rvert. \end{align*} $$
Proof. The first statement follows from [Reference Soundararajan62, Corollary 1.8(i)]. Using Deligne’s bound
![]() $\left \lvert \lambda _f(p)\right \rvert \le 2$
and applying [Reference Soundararajan62, Corollary 1.8(ii)], we will establish the second claim by the following simple induction argument. It suffices to show for each
$\left \lvert \lambda _f(p)\right \rvert \le 2$
and applying [Reference Soundararajan62, Corollary 1.8(ii)], we will establish the second claim by the following simple induction argument. It suffices to show for each
![]() $p\nmid 2\ell $
that
$p\nmid 2\ell $
that
 $$ \begin{align*} \left\lvert c\left(f,p^{2m} n\right)\right\rvert \le 3^m \lvert c(f,n)\rvert. \end{align*} $$
$$ \begin{align*} \left\lvert c\left(f,p^{2m} n\right)\right\rvert \le 3^m \lvert c(f,n)\rvert. \end{align*} $$
The case
![]() $m=0$
is trivial, and
$m=0$
is trivial, and
![]() $m=1$
follows from the first claim of the lemma. By [Reference Soundararajan62, Corollary 1.8(ii)], we have, for any
$m=1$
follows from the first claim of the lemma. By [Reference Soundararajan62, Corollary 1.8(ii)], we have, for any
![]() $m \ge 1$
,
$m \ge 1$
,
 $$ \begin{align*} c\left(f,p^{2m+2}n\right) =\lambda_f(p) c\left(f,p^{2m}n\right)-(-1)^{k\left(p^2-1\right)/2} c\left(f,p^{2m-2} n\right). \end{align*} $$
$$ \begin{align*} c\left(f,p^{2m+2}n\right) =\lambda_f(p) c\left(f,p^{2m}n\right)-(-1)^{k\left(p^2-1\right)/2} c\left(f,p^{2m-2} n\right). \end{align*} $$
Hence, for
![]() $m \ge 1$
we get
$m \ge 1$
we get
 $$ \begin{align*} \left\lvert c\left(f,p^{2m+2}n\right)\right\rvert &\le 2 \left\lvert c\left(f,p^{2m}n\right)\right\rvert+\left\lvert c\left(f,p^{2m-2 }n\right)\right\rvert\\ & \le \left(2 \cdot 3^{m}+3^{m-1}\right) \lvert c(f,n)\rvert \le 3^{m+1} \lvert c(f,n)\rvert. \end{align*} $$
$$ \begin{align*} \left\lvert c\left(f,p^{2m+2}n\right)\right\rvert &\le 2 \left\lvert c\left(f,p^{2m}n\right)\right\rvert+\left\lvert c\left(f,p^{2m-2 }n\right)\right\rvert\\ & \le \left(2 \cdot 3^{m}+3^{m-1}\right) \lvert c(f,n)\rvert \le 3^{m+1} \lvert c(f,n)\rvert. \end{align*} $$
2.4. An explicit version of Waldspurger’s formula
A well-known formula of Waldspurger [Reference Waldspurger67] that was refined and made explicit in special cases by Kohnen [Reference Kohnen34] expresses the squares of Fourier coefficients of half-integral-weight eigenforms in terms of central L-values. We state a version of it here for elements of the basis (13).
Proposition 2.2. Let
![]() $r, \ell $
be positive, odd, square-free integers with
$r, \ell $
be positive, odd, square-free integers with
![]() $(r, \ell )=1$
. Let f be a newform in
$(r, \ell )=1$
. Let f be a newform in
 $S^{+, \mathrm {new}}_{k+\frac 12}(4\ell )$
and let
$S^{+, \mathrm {new}}_{k+\frac 12}(4\ell )$
and let
![]() $g \in S_{2k}^{\mathrm {new}}(\ell )$
be the Shimura lift of f. Then for any square-free positive integer n with
$g \in S_{2k}^{\mathrm {new}}(\ell )$
be the Shimura lift of f. Then for any square-free positive integer n with
![]() $(n, 4\ell )=1$
, and
$(n, 4\ell )=1$
, and
![]() $d=(-1)^kn$
, we have
$d=(-1)^kn$
, we have
 $$ \begin{align*} \frac{\left\lvert c\left(f\mid U\left(r^2\right), n\right)\right\rvert^2}{\langle f, f\rangle} = 2^{\omega(\ell)} \frac{L\left(\frac12, g \otimes \chi_d \right)}{\langle g, g \rangle } \frac{(k-1)!}{\pi^k} \left(\prod_{p\mid r}\left(\lambda_f(p) - \frac{1}{\sqrt{p}}\left(\frac{d}{p} \right) \right)\right)^2, \end{align*} $$
$$ \begin{align*} \frac{\left\lvert c\left(f\mid U\left(r^2\right), n\right)\right\rvert^2}{\langle f, f\rangle} = 2^{\omega(\ell)} \frac{L\left(\frac12, g \otimes \chi_d \right)}{\langle g, g \rangle } \frac{(k-1)!}{\pi^k} \left(\prod_{p\mid r}\left(\lambda_f(p) - \frac{1}{\sqrt{p}}\left(\frac{d}{p} \right) \right)\right)^2, \end{align*} $$
provided that
-
i)
 $d \equiv 1 \pmod {4}$
and
$d \equiv 1 \pmod {4}$
and -
ii) for each prime
 $p\mid \ell $
, we have
$p\mid \ell $
, we have
 $\left (\frac {d}{p}\right )=w_p$
, where
$\left (\frac {d}{p}\right )=w_p$
, where
 $w_p$
is the eigenvalue for the Atkin–Lehner operator at p acting on g.
$w_p$
is the eigenvalue for the Atkin–Lehner operator at p acting on g.
If either of these two conditions is not met, then
 $c\left (f\mid U\left (r^2\right ), n\right ) = 0$
.
$c\left (f\mid U\left (r^2\right ), n\right ) = 0$
.
Proof. This follows from [Reference Kohnen34, Corollary 1], [Reference Kohnen33, Proposition 4], and Lemma 2.1.
2.5. Estimates on moments of Fourier coefficients
Proposition 2.3. Let
 $f \in S_{k+\frac 12}^+(4N)$
, where N is odd and square-free. Then there exists
$f \in S_{k+\frac 12}^+(4N)$
, where N is odd and square-free. Then there exists
![]() $M\ge 2$
such that for all sufficiently large X,
$M\ge 2$
such that for all sufficiently large X,
 $$ \begin{align} \sum_{\substack{X \leq n \leq MX \\ (n,2N)=1 }} \lvert c(f,n)\rvert^2 \mu^2(n) \asymp_{f, M} X, \end{align} $$
$$ \begin{align} \sum_{\substack{X \leq n \leq MX \\ (n,2N)=1 }} \lvert c(f,n)\rvert^2 \mu^2(n) \asymp_{f, M} X, \end{align} $$
and for any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
 $$ \begin{align} \sum_{\substack{X \leq n \leq 2X \\ (n,2N)=1}} \lvert c(f,n)\rvert^4 \mu^2(n) \ll_{f, \varepsilon} X^{1+\varepsilon}. \end{align} $$
$$ \begin{align} \sum_{\substack{X \leq n \leq 2X \\ (n,2N)=1}} \lvert c(f,n)\rvert^4 \mu^2(n) \ll_{f, \varepsilon} X^{1+\varepsilon}. \end{align} $$
Proof. We first prove the estimate (14). For the upper bound we use the fact that
![]() $y^{k+1/2}\lvert f(z)\rvert $
is bounded on
$y^{k+1/2}\lvert f(z)\rvert $
is bounded on
![]() $\mathbb H$
, and hence we have
$\mathbb H$
, and hence we have
 $$ \begin{align} \sum_{\substack{X \le n \le 2X \\ (n,2N)=1}} \lvert c(f,n)\rvert^2 \mu^2(n) \le \sum_{X \le n \le 2X} \lvert c(f,n)\rvert^2 & \ll \frac{1}{X^{k-1/2}} \sum_{n} \lvert c(f, n)\rvert^2 n^{k - \frac12} e^{-4\pi n /X}\nonumber\\ & = \frac{1}{X^{k-1/2}} \int_0^1 \lvert f(x+i/X)\rvert^2 dx \ll_f X. \end{align} $$
$$ \begin{align} \sum_{\substack{X \le n \le 2X \\ (n,2N)=1}} \lvert c(f,n)\rvert^2 \mu^2(n) \le \sum_{X \le n \le 2X} \lvert c(f,n)\rvert^2 & \ll \frac{1}{X^{k-1/2}} \sum_{n} \lvert c(f, n)\rvert^2 n^{k - \frac12} e^{-4\pi n /X}\nonumber\\ & = \frac{1}{X^{k-1/2}} \int_0^1 \lvert f(x+i/X)\rvert^2 dx \ll_f X. \end{align} $$
For the lower bound, we use a result obtained in the proof of [Reference Saha56, Proposition 3.7], which gives, for any
![]() $M \ge 1$
,
$M \ge 1$
,
 $$ \begin{align*} \sum_{(n,2N)=1} \lvert c(f, n)\rvert^2 \mu^2(n) e^{-n/\left(X\sqrt{M}\right)} \gg_f X\sqrt{M}. \end{align*} $$
$$ \begin{align*} \sum_{(n,2N)=1} \lvert c(f, n)\rvert^2 \mu^2(n) e^{-n/\left(X\sqrt{M}\right)} \gg_f X\sqrt{M}. \end{align*} $$
Using the bound (16) along with partial summation, we can bound the tail end of the sum as follows:
 $$ \begin{align*} \sum_{\substack{n \ge M X\\ (n,2N)=1}} \lvert c(f, n)\rvert^2 \mu^2(n) e^{-n/\left(X\sqrt{M}\right)} \ll_f M e^{-\sqrt{M}} X. \end{align*} $$
$$ \begin{align*} \sum_{\substack{n \ge M X\\ (n,2N)=1}} \lvert c(f, n)\rvert^2 \mu^2(n) e^{-n/\left(X\sqrt{M}\right)} \ll_f M e^{-\sqrt{M}} X. \end{align*} $$
Combining the two bounds, we have, for M sufficiently large,
 $$ \begin{align*} \sum_{\substack{n \le M X\\ (n,2N)=1}} \lvert c(f,n)\rvert^2 \mu^2(n) & \ge \sum_{\substack{n \le MX\\ (n,2N)=1}} \lvert c(f, n)\rvert^2 \mu^2(n) e^{-n/\left(X\sqrt{M}\right)} \\ &= \sum_{\substack{n \ge 1\\ (n,2N)=1}} \lvert c(f, n)\rvert^2 \mu^2(n) e^{-n/\left(X\sqrt{M}\right)} +O_f \!\left(\! M e^{-\sqrt{M}} X \!\right)\! \gg_f X \sqrt{M}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{n \le M X\\ (n,2N)=1}} \lvert c(f,n)\rvert^2 \mu^2(n) & \ge \sum_{\substack{n \le MX\\ (n,2N)=1}} \lvert c(f, n)\rvert^2 \mu^2(n) e^{-n/\left(X\sqrt{M}\right)} \\ &= \sum_{\substack{n \ge 1\\ (n,2N)=1}} \lvert c(f, n)\rvert^2 \mu^2(n) e^{-n/\left(X\sqrt{M}\right)} +O_f \!\left(\! M e^{-\sqrt{M}} X \!\right)\! \gg_f X \sqrt{M}. \end{align*} $$
Finally, we note that by the bound (16) the contribution from terms to the left-hand side here with
![]() $n \le X$
is
$n \le X$
is
![]() $O_f(X)$
, which completes the proof of the lower bound in the estimate (14).
$O_f(X)$
, which completes the proof of the lower bound in the estimate (14).
For the proof of the bound (15), we use equation (13) to reduce to the case
 $f = f_1\mid U\left (r^2\right )$
, where
$f = f_1\mid U\left (r^2\right )$
, where
 $f_1 \in S^{+, \mathrm {new}}_{k+\frac 12}(4\ell )$
is a newform with
$f_1 \in S^{+, \mathrm {new}}_{k+\frac 12}(4\ell )$
is a newform with
![]() $r\ell \mid N$
. Using Proposition 2.2, it now suffices to prove that
$r\ell \mid N$
. Using Proposition 2.2, it now suffices to prove that
 $$ \begin{align*} \sideset{}{^{\flat}}\sum_{\lvert d\rvert\le X} L\left(\tfrac12, g \otimes \chi_d\right)^2 \ll_{g, \varepsilon} X^{1+\varepsilon}, \end{align*} $$
$$ \begin{align*} \sideset{}{^{\flat}}\sum_{\lvert d\rvert\le X} L\left(\tfrac12, g \otimes \chi_d\right)^2 \ll_{g, \varepsilon} X^{1+\varepsilon}, \end{align*} $$
where g is the Shimura lift of
![]() $f_1$
and the sum is over fundamental discriminants d. This follows from the approximate functional equation and Heath-Brown’s quadratic large sieve [Reference Henniart25], using a straightforward modification of the proof of [Reference Henniart25, Theorem 2] (see also [Reference Soundararajan and Young65, Corollary 2.5]).
$f_1$
and the sum is over fundamental discriminants d. This follows from the approximate functional equation and Heath-Brown’s quadratic large sieve [Reference Henniart25], using a straightforward modification of the proof of [Reference Henniart25, Theorem 2] (see also [Reference Soundararajan and Young65, Corollary 2.5]).
3. Sign changes for coefficients of half-integral-weight forms
3.1. Statement of main result
Throughout this section, let
![]() $k \ge 2$
be an integer and
$k \ge 2$
be an integer and
![]() $N \ge 1$
be odd and square-free. The main theorem to be proved in this section is the following:
$N \ge 1$
be odd and square-free. The main theorem to be proved in this section is the following:
Theorem 3.1. Let
 $f \in S_{k+\frac 12}^+(4N)$
be a fixed cusp form whose Fourier coefficients
$f \in S_{k+\frac 12}^+(4N)$
be a fixed cusp form whose Fourier coefficients
![]() $c(f,n)$
are all real. Then there exists
$c(f,n)$
are all real. Then there exists
![]() $M \ge 2$
such that given any
$M \ge 2$
such that given any
![]() $\varepsilon>0$
, the sequence
$\varepsilon>0$
, the sequence
 $\{ c(f,n) \}_{\substack {X \leq n \leq MX \\ 2n \text { is square-free}\\ (n,N)=1}}$
has at least
$\{ c(f,n) \}_{\substack {X \leq n \leq MX \\ 2n \text { is square-free}\\ (n,N)=1}}$
has at least
![]() $ \gg _{f,M,\varepsilon } X^{1-\varepsilon }$
sign changes.
$ \gg _{f,M,\varepsilon } X^{1-\varepsilon }$
sign changes.
The main novelty here is that this result holds for all cusp forms
 $f \in S_{k+1/2}^+(4N)$
, not just Hecke eigenforms, and this is crucial for our later application. Previously it was not apparently even known that there are infinitely many sign changes of
$f \in S_{k+1/2}^+(4N)$
, not just Hecke eigenforms, and this is crucial for our later application. Previously it was not apparently even known that there are infinitely many sign changes of
![]() $c(f,n)$
as n ranges over square-free integers for
$c(f,n)$
as n ranges over square-free integers for
 $f \in S_{k+\frac 12}^+(4N)$
.
$f \in S_{k+\frac 12}^+(4N)$
.
Our proof builds upon the methods developed in [Reference Lester and Radziwiłł39, Reference Matomäki and Radziwiłł42] and relies upon the following two propositions. The first shows that the size of
![]() $\lvert c(f,n)\rvert $
is relatively well behaved for most short intervals
$\lvert c(f,n)\rvert $
is relatively well behaved for most short intervals
![]() $[x,x+y]$
.
$[x,x+y]$
.
Proposition 3.2. Let
 $f \in S_{k+\frac {1}{2}}^+(4N)$
. There exists
$f \in S_{k+\frac {1}{2}}^+(4N)$
. There exists
![]() $M \ge 2$
such that given any
$M \ge 2$
such that given any
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $2 \le y \le X/2$
, there are
$2 \le y \le X/2$
, there are
 $\gg _{f,M,\varepsilon } X^{1-\frac 32 \varepsilon }$
integers
$\gg _{f,M,\varepsilon } X^{1-\frac 32 \varepsilon }$
integers
![]() $X \le x \le MX$
such that
$X \le x \le MX$
such that
 $$ \begin{align*} \sum_{\substack{x \leq n \leq x + y \\ (n,2N)=1}} \lvert c(f, n)\rvert \mu^2(n)> \frac{y}{X^{\varepsilon}}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{x \leq n \leq x + y \\ (n,2N)=1}} \lvert c(f, n)\rvert \mu^2(n)> \frac{y}{X^{\varepsilon}}. \end{align*} $$
Our other main proposition shows that we can obtain square-root cancelation in sums of
![]() $c(f,n)$
over almost all short intervals
$c(f,n)$
over almost all short intervals
![]() $[x,x+y]$
.
$[x,x+y]$
.
Proposition 3.3. Let
 $f \in S_{k+\frac {1}{2}}^+(4N)$
. Then for
$f \in S_{k+\frac {1}{2}}^+(4N)$
. Then for
 $1 \leq y \leq X^{\frac {1}{205}}$
, we have
$1 \leq y \leq X^{\frac {1}{205}}$
, we have
 $$ \begin{align*} \sum_{X \le x \le 2X} \left\lvert\sum_{\substack{x \le n \le x+y \\ (n,2N)=1}} c(f,n) \mu^2(n) \right\rvert \ll_f X \sqrt{y}. \end{align*} $$
$$ \begin{align*} \sum_{X \le x \le 2X} \left\lvert\sum_{\substack{x \le n \le x+y \\ (n,2N)=1}} c(f,n) \mu^2(n) \right\rvert \ll_f X \sqrt{y}. \end{align*} $$
We will now prove Theorem 3.1 using Propositions 3.2 and 3.3. The proofs of Propositions 3.2 and 3.3 will be given in §§3.2 and 3.3, respectively.
Proof of Theorem 3.1. Observe that if the Fourier coefficients
![]() $c(f,n)$
are real and
$c(f,n)$
are real and
 $$ \begin{align*} \left\lvert \sum_{\substack{x \leq n \leq x + y \\ (n,2N)=1}} c(f,n) \mu^2(n) \right\rvert < \sum_{\substack{x \leq n \leq x + y \\ (n,2N)=1}} \lvert c(f,n)\rvert \mu^2(n), \end{align*} $$
$$ \begin{align*} \left\lvert \sum_{\substack{x \leq n \leq x + y \\ (n,2N)=1}} c(f,n) \mu^2(n) \right\rvert < \sum_{\substack{x \leq n \leq x + y \\ (n,2N)=1}} \lvert c(f,n)\rvert \mu^2(n), \end{align*} $$
then the interval
![]() $[x,x+y]$
must contain a sign change of
$[x,x+y]$
must contain a sign change of
![]() $c(f,n)$
, where
$c(f,n)$
, where
![]() $n\in [x,x+y]$
ranges over odd square-free integers that are coprime to N. We will show that for most integers
$n\in [x,x+y]$
ranges over odd square-free integers that are coprime to N. We will show that for most integers
![]() $X \le x \le MX$
, this inequality holds for intervals of length
$X \le x \le MX$
, this inequality holds for intervals of length
![]() $y = X^{6 \varepsilon }$
.
$y = X^{6 \varepsilon }$
.
By Chebyshev’s inequality, the number of integers
![]() $X \le x \le MX$
for which
$X \le x \le MX$
for which
 $$ \begin{align} \left\lvert \sum_{\substack{x \leq n \leq x + y \\ (n,2N)=1}} c(f,n) \mu^2(n) \right\rvert \leq \frac{y}{X^{\varepsilon}} \end{align} $$
$$ \begin{align} \left\lvert \sum_{\substack{x \leq n \leq x + y \\ (n,2N)=1}} c(f,n) \mu^2(n) \right\rvert \leq \frac{y}{X^{\varepsilon}} \end{align} $$
does not hold is
 $$ \begin{align*} \le \frac{X^{\varepsilon}}{y}\sum_{X \le x \le MX} \left\lvert \sum_{\substack{x \leq n \leq x + y \\ (n,2N)=1}} c(f,n) \mu^2(n) \right\rvert \ll_{f,M} \frac{X^{1+\varepsilon}}{\sqrt{y}}=X^{1-2\varepsilon}, \end{align*} $$
$$ \begin{align*} \le \frac{X^{\varepsilon}}{y}\sum_{X \le x \le MX} \left\lvert \sum_{\substack{x \leq n \leq x + y \\ (n,2N)=1}} c(f,n) \mu^2(n) \right\rvert \ll_{f,M} \frac{X^{1+\varepsilon}}{\sqrt{y}}=X^{1-2\varepsilon}, \end{align*} $$
where we have used Proposition 3.3 in the last inequality. By Proposition 3.2, we have
 $$ \begin{align} \sum_{\substack{x \leq n \leq x + y \\ (n,2N)=1}} \lvert c(f,n)\rvert \mu^2(n)> \frac{y}{X^{\varepsilon}} \end{align} $$
$$ \begin{align} \sum_{\substack{x \leq n \leq x + y \\ (n,2N)=1}} \lvert c(f,n)\rvert \mu^2(n)> \frac{y}{X^{\varepsilon}} \end{align} $$
for all integers
![]() $X \le x \le MX$
outside an exceptional set of size
$X \le x \le MX$
outside an exceptional set of size
![]() $\ll _{f,M, \varepsilon } X^{1 - 3\varepsilon /2}$
. Hence, there exist at least
$\ll _{f,M, \varepsilon } X^{1 - 3\varepsilon /2}$
. Hence, there exist at least
![]() $\gg _{f, M, \varepsilon } X^{1 - 3 \varepsilon /2}$
integers
$\gg _{f, M, \varepsilon } X^{1 - 3 \varepsilon /2}$
integers
![]() $X \le x \le MX$
such that the bounds (17) and (18) hold. Therefore, we obtain at least
$X \le x \le MX$
such that the bounds (17) and (18) hold. Therefore, we obtain at least
 $ \gg _{f, M, \varepsilon } \frac {X^{1-3\varepsilon /2}}{y}=X^{1 - 15 \varepsilon /2}$
sign changes of
$ \gg _{f, M, \varepsilon } \frac {X^{1-3\varepsilon /2}}{y}=X^{1 - 15 \varepsilon /2}$
sign changes of
![]() $c(f,n)$
along integers
$c(f,n)$
along integers
![]() $X \le n \le MX$
that are odd, square-free, and coprime to N.□
$X \le n \le MX$
that are odd, square-free, and coprime to N.□
3.2. Proof of Proposition 3.2
We first prove the following result, which is an easy consequence of Proposition 2.3:
Lemma 3.4. Let
 $f \in S_{k+\frac 12}^{+}(4N)$
. Then there exists
$f \in S_{k+\frac 12}^{+}(4N)$
. Then there exists
![]() $M \ge 2$
such that given any
$M \ge 2$
such that given any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
 $$ \begin{align} \sum_{\substack{X \le n \le MX \\ (n,2N)=1 \\ \lvert c(f,n)\rvert \le X^{\varepsilon}}} \lvert c(f,n)\rvert \mu^2(n) \gg_{f,M,\varepsilon} X^{1-\varepsilon/2}. \end{align} $$
$$ \begin{align} \sum_{\substack{X \le n \le MX \\ (n,2N)=1 \\ \lvert c(f,n)\rvert \le X^{\varepsilon}}} \lvert c(f,n)\rvert \mu^2(n) \gg_{f,M,\varepsilon} X^{1-\varepsilon/2}. \end{align} $$
Proof. Applying Hölder’s inequality gives
 $$ \begin{align*} \sum_{\substack{X \leq n \leq MX \\ (n,2N)=1}} \lvert c(f, n)\rvert^2 \mu^2(n) \le \left( \sum_{\substack{X \leq n \leq MX \\ (n,2N)=1}} \lvert c(f,n)\rvert \mu^2(n) \right)^{2/3} \left( \sum_{\substack{X \leq n \leq MX \\ (n,2N)=1}} \lvert c(f,n)\rvert^4 \mu^2(n) \right)^{1/3}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{X \leq n \leq MX \\ (n,2N)=1}} \lvert c(f, n)\rvert^2 \mu^2(n) \le \left( \sum_{\substack{X \leq n \leq MX \\ (n,2N)=1}} \lvert c(f,n)\rvert \mu^2(n) \right)^{2/3} \left( \sum_{\substack{X \leq n \leq MX \\ (n,2N)=1}} \lvert c(f,n)\rvert^4 \mu^2(n) \right)^{1/3}. \end{align*} $$
Hence, using Proposition 2.3 we conclude that
 $$ \begin{align} \sum_{\substack{X \le n \le MX \\ (n,2N)=1}} \lvert c(f,n)\rvert \mu^2(n) \gg_{f, M, \varepsilon} X^{1-\varepsilon/2}. \end{align} $$
$$ \begin{align} \sum_{\substack{X \le n \le MX \\ (n,2N)=1}} \lvert c(f,n)\rvert \mu^2(n) \gg_{f, M, \varepsilon} X^{1-\varepsilon/2}. \end{align} $$
Also, by the estimate (14) we have
 $$ \begin{align*} \sum_{\substack{X \le n \le MX \\ (n,2N)=1 \\ \lvert c(f,n)\rvert> X^{\varepsilon}}} \lvert c(f,n)\rvert \mu^2(n) < X^{-\varepsilon} \sum_{\substack{X \le n \le MX \\ (n,2N)=1}} \lvert c(f,n)\rvert^2 \mu^2(n)\ll_{f,M, \varepsilon} X^{1-\varepsilon}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{X \le n \le MX \\ (n,2N)=1 \\ \lvert c(f,n)\rvert> X^{\varepsilon}}} \lvert c(f,n)\rvert \mu^2(n) < X^{-\varepsilon} \sum_{\substack{X \le n \le MX \\ (n,2N)=1}} \lvert c(f,n)\rvert^2 \mu^2(n)\ll_{f,M, \varepsilon} X^{1-\varepsilon}. \end{align*} $$
Combining this with the bound (20) completes the proof.
Proof of Proposition 3.2. Let
 $C(f,n)=\lvert c(f,n)\rvert \mu ^2(n) 1_{(n,2N)=1} 1_{\lvert c(f,n)\rvert \le X^{\varepsilon }}$
. Applying Lemma 3.4, we see that
$C(f,n)=\lvert c(f,n)\rvert \mu ^2(n) 1_{(n,2N)=1} 1_{\lvert c(f,n)\rvert \le X^{\varepsilon }}$
. Applying Lemma 3.4, we see that
 $$ \begin{align*} X^{1-\varepsilon/2} \ll_{f,M, \varepsilon} \sum_{\substack{ X+y \le n \le 2MX }} C(f,n) \le \frac{1}{y} \sum_{X \le x \le 2MX} \sum_{\substack{ x \le n \le x+y}} C(f,n) , \end{align*} $$
$$ \begin{align*} X^{1-\varepsilon/2} \ll_{f,M, \varepsilon} \sum_{\substack{ X+y \le n \le 2MX }} C(f,n) \le \frac{1}{y} \sum_{X \le x \le 2MX} \sum_{\substack{ x \le n \le x+y}} C(f,n) , \end{align*} $$
where the second inequality follows because every term in the sum on the left-hand side is counted
![]() $\lfloor y\rfloor +1$
times on the right-hand side. Let
$\lfloor y\rfloor +1$
times on the right-hand side. Let
 $S=\{X \le x \le 2MX : \sum _{x \le n \le x+y} C(f,n) \le y/X^{\varepsilon }\}$
. The contribution to the right-hand side from the integers
$S=\{X \le x \le 2MX : \sum _{x \le n \le x+y} C(f,n) \le y/X^{\varepsilon }\}$
. The contribution to the right-hand side from the integers
![]() $x \in S$
is
$x \in S$
is
 $\ll _{f,M,\varepsilon }\frac {1}{y} \cdot X \frac {y}{X^{\varepsilon }}=X^{1-\varepsilon }$
. Hence we must have
$\ll _{f,M,\varepsilon }\frac {1}{y} \cdot X \frac {y}{X^{\varepsilon }}=X^{1-\varepsilon }$
. Hence we must have
 $$ \begin{align*} X^{1-\varepsilon/2} \ll_{f,M,\varepsilon} \frac{1}{y} \sum_{\substack{X \le x \le 2MX \\ x \notin S}}\sum_{\substack{ x \le n \le x+y \\ }} C(f,n) \ll_{f,M, \varepsilon} \frac{1}{y} \cdot y X^{\varepsilon} \sum_{\substack{X \le x \le 2MX \\ x \notin S}} 1, \end{align*} $$
$$ \begin{align*} X^{1-\varepsilon/2} \ll_{f,M,\varepsilon} \frac{1}{y} \sum_{\substack{X \le x \le 2MX \\ x \notin S}}\sum_{\substack{ x \le n \le x+y \\ }} C(f,n) \ll_{f,M, \varepsilon} \frac{1}{y} \cdot y X^{\varepsilon} \sum_{\substack{X \le x \le 2MX \\ x \notin S}} 1, \end{align*} $$
so that
 $\# \left \{ X \le x \le 2MX : x \notin S\right \} \gg _{f,M, \varepsilon } X^{1-\frac 32 \varepsilon }$
.□
$\# \left \{ X \le x \le 2MX : x \notin S\right \} \gg _{f,M, \varepsilon } X^{1-\frac 32 \varepsilon }$
.□
3.3. Proof of Proposition 3.3
Throughout this section, we write
 $$ \begin{align} W(u)=u^{\frac{k-1/2}{2}}e^{-2\pi u}. \end{align} $$
$$ \begin{align} W(u)=u^{\frac{k-1/2}{2}}e^{-2\pi u}. \end{align} $$
The proof of the proposition proceeds directly, beginning with an application of Cauchy–Schwarz. This leads naturally to a shifted convolution sum of Fourier coefficients of f over square-free integers, and to bound this sum we require the following fairly standard result:
Proposition 3.5. Let
 $f \in S^+_{k+\frac 12}(4N)$
. Then for
$f \in S^+_{k+\frac 12}(4N)$
. Then for
![]() $1 \leq r\leq X^{\frac {1}{102}}$
,
$1 \leq r\leq X^{\frac {1}{102}}$
,
 $0 < \lvert h\rvert < X^{\frac {1}{2}}$
, and
$0 < \lvert h\rvert < X^{\frac {1}{2}}$
, and
![]() $v\in \mathbb Z$
with
$v\in \mathbb Z$
with
![]() $(v, r) = 1$
, we have, for any given
$(v, r) = 1$
, we have, for any given
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
,
 $$ \begin{align} \sum_{n \ge 1} c(f,n) c(f,n+h) e \left ( \frac{n v}{r} \right ) W\left(\frac{n}{X} \right) W\left( \frac{n+h}{X}\right) \ll_{f,\varepsilon} X^{1 - \frac{1}{102} + \varepsilon}. \end{align} $$
$$ \begin{align} \sum_{n \ge 1} c(f,n) c(f,n+h) e \left ( \frac{n v}{r} \right ) W\left(\frac{n}{X} \right) W\left( \frac{n+h}{X}\right) \ll_{f,\varepsilon} X^{1 - \frac{1}{102} + \varepsilon}. \end{align} $$
Proof. This is an extension of [Reference Lester and Radziwiłł39, Proposition 6.1] to the case of general level, and we will describe how to adapt the arguments given there to this case. The initial step is to use the Fourier expansion of f to express the left-hand side of formula (22) as
 $$ \begin{align*} =\frac{1}{X^{k-\frac12}} \int_0^1 f\left(\alpha+\frac{v}{q}+\frac{i}{X} \right) f\left(-\alpha+\frac{i}{X} \right) e(-\alpha h) d\alpha. \end{align*} $$
$$ \begin{align*} =\frac{1}{X^{k-\frac12}} \int_0^1 f\left(\alpha+\frac{v}{q}+\frac{i}{X} \right) f\left(-\alpha+\frac{i}{X} \right) e(-\alpha h) d\alpha. \end{align*} $$
We now use the circle method following Jutila [Reference Jutila30], as in [Reference Andrianov2 Reference Arthur3, Proposition 2]. An important feature in Jutila’s version of the circle method is that we have freedom over our choice of moduli, which we choose as follows:
Write
 $R=\sum _{q \in \mathcal Q} \varphi (q)$
. Upon applying [Reference Andrianov2
Reference Arthur3, Proposition 2] with
$R=\sum _{q \in \mathcal Q} \varphi (q)$
. Upon applying [Reference Andrianov2
Reference Arthur3, Proposition 2] with
![]() $\delta =Q^{-2+\eta }$
,
$\delta =Q^{-2+\eta }$
,
![]() $Q=X^{1/2+2\eta }$
, and
$Q=X^{1/2+2\eta }$
, and
![]() $r \le X^{\eta /8}$
, where
$r \le X^{\eta /8}$
, where
![]() $\eta>0$
is chosen later, we get that up to a term of size
$\eta>0$
is chosen later, we get that up to a term of size
 $O_f\left (X^{1-\eta /8+\varepsilon }\right )$
the integral equals
$O_f\left (X^{1-\eta /8+\varepsilon }\right )$
the integral equals
 $$ \begin{align} \frac{Q^{2-\eta}}{2 R X^{k - \frac 12}}\sum_{q \in \mathcal{Q}\ } \sideset{}{^*}\sum_{d \! \!\!\! \pmod q} e \!\left(-\tfrac{h d}{q}\right)\! \int_{-\delta}^{\delta} f \left(\tfrac{d}{q}+\tfrac{v}{r}+\alpha+\tfrac{i}{X}\right) f\left(\tfrac{-d}{q}-\alpha+\tfrac{i}{X}\right) e (- \alpha h) d \alpha. \end{align} $$
$$ \begin{align} \frac{Q^{2-\eta}}{2 R X^{k - \frac 12}}\sum_{q \in \mathcal{Q}\ } \sideset{}{^*}\sum_{d \! \!\!\! \pmod q} e \!\left(-\tfrac{h d}{q}\right)\! \int_{-\delta}^{\delta} f \left(\tfrac{d}{q}+\tfrac{v}{r}+\alpha+\tfrac{i}{X}\right) f\left(\tfrac{-d}{q}-\alpha+\tfrac{i}{X}\right) e (- \alpha h) d \alpha. \end{align} $$
Notably, to estimate the error term we use the fact that
 $y^{\frac {k}{2} + \frac 14} \lvert f(z)\rvert $
is bounded on
$y^{\frac {k}{2} + \frac 14} \lvert f(z)\rvert $
is bounded on
![]() $\mathbb H$
, since f is a cusp form.
$\mathbb H$
, since f is a cusp form.
Since we have chosen our moduli
![]() $q \in \mathcal Q$
such that
$q \in \mathcal Q$
such that
![]() $4N\mid q$
, we are able to use the modularity of f by applying [Reference Lester and Radziwiłł39, Lemma 6.1], which extends to general level in straightforward way, then once again use the Fourier expansion of f. Consequently, we have transformed the original sum on the left-hand side of formula (22), which is effectively over
$4N\mid q$
, we are able to use the modularity of f by applying [Reference Lester and Radziwiłł39, Lemma 6.1], which extends to general level in straightforward way, then once again use the Fourier expansion of f. Consequently, we have transformed the original sum on the left-hand side of formula (22), which is effectively over
![]() $n\le X^{1+\varepsilon }$
, to dual sums which are effectively over
$n\le X^{1+\varepsilon }$
, to dual sums which are effectively over
![]() $m,n \le X^{\varepsilon } Q^2/X $
. The summands in the dual sums include the Fourier coefficients of f twisted by additive characters and factors from the half-integral-weight multiplier system, along with a Kloosterman sum
$m,n \le X^{\varepsilon } Q^2/X $
. The summands in the dual sums include the Fourier coefficients of f twisted by additive characters and factors from the half-integral-weight multiplier system, along with a Kloosterman sum
![]() $S(\star , -h;p)$
, where the first argument
$S(\star , -h;p)$
, where the first argument
![]() $\star $
depends on
$\star $
depends on
![]() $N,p,m,n,v,r$
. An important observation is that since p is a prime with
$N,p,m,n,v,r$
. An important observation is that since p is a prime with
![]() $0< \lvert h\rvert < p$
, the Weil bound gives
$0< \lvert h\rvert < p$
, the Weil bound gives
![]() $\lvert S(\star , -h;p)\rvert \le 2\sqrt {p}$
for any
$\lvert S(\star , -h;p)\rvert \le 2\sqrt {p}$
for any
![]() $\star \in \mathbb Z$
. Using the Weil bound and estimating the dual sums over
$\star \in \mathbb Z$
. Using the Weil bound and estimating the dual sums over
![]() $m,n$
by applying Cauchy–Schwarz and formula (16) to handle the Fourier coefficients of f, we can show that expression (23) is bounded by
$m,n$
by applying Cauchy–Schwarz and formula (16) to handle the Fourier coefficients of f, we can show that expression (23) is bounded by
 $$ \begin{align*} \ll_{f, \varepsilon} X^{3/4+49\eta/16+\varepsilon}. \end{align*} $$
$$ \begin{align*} \ll_{f, \varepsilon} X^{3/4+49\eta/16+\varepsilon}. \end{align*} $$
Recalling our earlier error term of
 $O\left (X^{1-\eta /8+\varepsilon }\right )$
, which arose from applying Jutila’s circle method, we now take
$O\left (X^{1-\eta /8+\varepsilon }\right )$
, which arose from applying Jutila’s circle method, we now take
![]() $\eta =4/51$
to complete the proof.
$\eta =4/51$
to complete the proof.
To sum over square-free integers, we will sieve out integers that have a square divisor and require the following estimate for sums of Fourier coefficients:
Lemma 3.6. Let
 $f \in S_{k+\frac 12}^+(4N)$
. Then
$f \in S_{k+\frac 12}^+(4N)$
. Then
 $$ \begin{align*} \sum_{\substack{n \le X \\ (n,2N)=1 \\ d^2 \mid n }} \lvert c(f,n)\rvert \ll_{f,\varepsilon} \frac{X^{1+\varepsilon}}{d^2}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{n \le X \\ (n,2N)=1 \\ d^2 \mid n }} \lvert c(f,n)\rvert \ll_{f,\varepsilon} \frac{X^{1+\varepsilon}}{d^2}. \end{align*} $$
Proof. Just as in the proof of Proposition 2.3, using equation (13) it suffices to consider the case
 $f=f_1\mid U\left (r^2\right )$
, where
$f=f_1\mid U\left (r^2\right )$
, where
 $f_1 \in S_{k+\frac 12}^{+,\text {new}}(4\ell )$
is a newform with
$f_1 \in S_{k+\frac 12}^{+,\text {new}}(4\ell )$
is a newform with
![]() $r\ell \mid N$
. For
$r\ell \mid N$
. For
![]() $(n,2N)=1$
write
$(n,2N)=1$
write
![]() $n=s^2m$
, where m is odd and square-free. Also, let
$n=s^2m$
, where m is odd and square-free. Also, let
![]() $t=rs$
and note
$t=rs$
and note
![]() $(t,\ell )=1$
, since N is square-free. Applying Lemma 2.1 we have
$(t,\ell )=1$
, since N is square-free. Applying Lemma 2.1 we have
 $$ \begin{align*} c\left(f_1\mid U\left(r^2\right),n\right)=c\left(f_1, t^2 m\right) \ll_\varepsilon t^{\varepsilon} \lvert c(f_1,m)\rvert. \end{align*} $$
$$ \begin{align*} c\left(f_1\mid U\left(r^2\right),n\right)=c\left(f_1, t^2 m\right) \ll_\varepsilon t^{\varepsilon} \lvert c(f_1,m)\rvert. \end{align*} $$
Using this bound and then applying Cauchy–Schwarz and the bound (16), we get
 $$ \begin{align*} \sum_{\substack{n \le X \\ (n,2N)=1 \\ d^2 \mid n }} \left\lvert c\left(f_1\mid U\left(r^2\right),n\right)\right\rvert \ll_\varepsilon X^{\varepsilon} \sum_{\substack{t \le \sqrt{X} \\ d\mid t}} \sum_{ m \le \frac{X}{t^2} } \lvert c(f_1,m)\rvert \ll_{f, \varepsilon} X^{\varepsilon} \sum_{\substack{t \le \sqrt{X} \\ d\mid t}} \frac{X}{t^2} \ll_\varepsilon \frac{X^{1+\varepsilon}}{d^2}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{n \le X \\ (n,2N)=1 \\ d^2 \mid n }} \left\lvert c\left(f_1\mid U\left(r^2\right),n\right)\right\rvert \ll_\varepsilon X^{\varepsilon} \sum_{\substack{t \le \sqrt{X} \\ d\mid t}} \sum_{ m \le \frac{X}{t^2} } \lvert c(f_1,m)\rvert \ll_{f, \varepsilon} X^{\varepsilon} \sum_{\substack{t \le \sqrt{X} \\ d\mid t}} \frac{X}{t^2} \ll_\varepsilon \frac{X^{1+\varepsilon}}{d^2}. \end{align*} $$
Proof of Proposition 3.3. To handle the condition that
![]() $2n$
be square-free, we first recall that the indicator function of square-free numbers is
$2n$
be square-free, we first recall that the indicator function of square-free numbers is
 $\mu ^2(n)=\sum _{d^2\mid n} \mu (d)$
. We then treat the cases of divisors
$\mu ^2(n)=\sum _{d^2\mid n} \mu (d)$
. We then treat the cases of divisors
![]() $d\le Y$
and
$d\le Y$
and
![]() $d>Y$
separately, letting
$d>Y$
separately, letting
 $$ \begin{align*} \mu^2_{\leq Y}(n) = \sum_{\substack{d^2 \mid n \\ d \leq Y }} \mu(d) , \qquad \mu^2_{> Y}(n) = \sum_{\substack{d^2 \mid n \\ d > Y}} \mu(d). \end{align*} $$
$$ \begin{align*} \mu^2_{\leq Y}(n) = \sum_{\substack{d^2 \mid n \\ d \leq Y }} \mu(d) , \qquad \mu^2_{> Y}(n) = \sum_{\substack{d^2 \mid n \\ d > Y}} \mu(d). \end{align*} $$
First we consider the large divisors, and get
 $$ \begin{align*} \sum_{X \leq x \leq 2X} \left\lvert\sum_{\substack{x \leq n \leq x + y \\ (n,2N)=1}} c(f,n) \mu^2_{>Y }(n) \right\rvert \leq y \sum_{\substack{n \leq 4 X \\ (n,2N)=1}} \left\lvert c(f,n) \mu^2_{> Y}(n)\right\rvert. \end{align*} $$
$$ \begin{align*} \sum_{X \leq x \leq 2X} \left\lvert\sum_{\substack{x \leq n \leq x + y \\ (n,2N)=1}} c(f,n) \mu^2_{>Y }(n) \right\rvert \leq y \sum_{\substack{n \leq 4 X \\ (n,2N)=1}} \left\lvert c(f,n) \mu^2_{> Y}(n)\right\rvert. \end{align*} $$
Using the definition of
![]() $\mu ^2_{> Y}(n)$
and applying Lemma 3.6, we see that the right-hand side of this inequality is
$\mu ^2_{> Y}(n)$
and applying Lemma 3.6, we see that the right-hand side of this inequality is
 $$ \begin{align} \ll y \sum_{\substack{d> Y }} \sum_{\substack{n \leq 4 X \\ d^2 \mid n}} \lvert c(f,n) \rvert \ll_{f, \varepsilon} y X^{1+\varepsilon} \sum_{d >Y} \frac{1}{d^2} \ll y \frac{X^{1+\varepsilon}}{Y}. \end{align} $$
$$ \begin{align} \ll y \sum_{\substack{d> Y }} \sum_{\substack{n \leq 4 X \\ d^2 \mid n}} \lvert c(f,n) \rvert \ll_{f, \varepsilon} y X^{1+\varepsilon} \sum_{d >Y} \frac{1}{d^2} \ll y \frac{X^{1+\varepsilon}}{Y}. \end{align} $$
For
![]() $ Y \ge \sqrt {y}X^{\varepsilon }$
, this is
$ Y \ge \sqrt {y}X^{\varepsilon }$
, this is
![]() $\ll X \sqrt {y}$
, as needed.
$\ll X \sqrt {y}$
, as needed.
Next we consider the contribution from the small divisors
![]() $d \le Y$
. Let
$d \le Y$
. Let
 $\widetilde C(f,n)=c(f,n)\mu _{\le Y}^2(n)1_{\left (n,2N\right )=1}$
. Applying Cauchy–Schwarz and using the fact that
$\widetilde C(f,n)=c(f,n)\mu _{\le Y}^2(n)1_{\left (n,2N\right )=1}$
. Applying Cauchy–Schwarz and using the fact that
![]() $W(u)^2 \gg 1$
, for any
$W(u)^2 \gg 1$
, for any
![]() $u \in [1,2]$
we get
$u \in [1,2]$
we get
 $$ \begin{align*} \sum_{X \le x \le 2 X} \left \lvert \sum_{x \le n \le x+y} \widetilde C(f,n) \right\rvert & \le \sqrt{X} \left( \sum_{X \le x \le 2X} \left \lvert \sum_{x \le n \le x + y} \widetilde C(f,n) \right \rvert^2\right)^{1/2} \\ & \ll \sqrt{X} \left( \sum_{x \ge 1} \left\lvert \sum_{x \le n \le x + y } \widetilde C(f,n) \right \rvert^2 W\left( \frac{x}{X}\right)^2\right)^{1/2}. \end{align*} $$
$$ \begin{align*} \sum_{X \le x \le 2 X} \left \lvert \sum_{x \le n \le x+y} \widetilde C(f,n) \right\rvert & \le \sqrt{X} \left( \sum_{X \le x \le 2X} \left \lvert \sum_{x \le n \le x + y} \widetilde C(f,n) \right \rvert^2\right)^{1/2} \\ & \ll \sqrt{X} \left( \sum_{x \ge 1} \left\lvert \sum_{x \le n \le x + y } \widetilde C(f,n) \right \rvert^2 W\left( \frac{x}{X}\right)^2\right)^{1/2}. \end{align*} $$
Assume
![]() $y \le X^{1/4}$
. We use the convention that
$y \le X^{1/4}$
. We use the convention that
![]() $c(f,n)=0$
if
$c(f,n)=0$
if
![]() $n \notin \mathbb N$
. To estimate the inner sums on the right-hand side, we expand the square, combine appropriate terms, use the fact that W is a smooth function, and apply the bound (16); the right-hand side then equals
$n \notin \mathbb N$
. To estimate the inner sums on the right-hand side, we expand the square, combine appropriate terms, use the fact that W is a smooth function, and apply the bound (16); the right-hand side then equals
 $$ \begin{align} &=\sum_{0 \leq h_1, h_2 \leq y} \sum_{\substack{n \ge 1 }} \widetilde C(f,n+h_1)\widetilde C(f,n+h_2) W\left(\frac{n}{X} \right)^2\nonumber \\ &= \sum_{\substack{\lvert h\rvert \leq y}} \sum_{\substack{n \ge 1}} \widetilde C(f,n) \widetilde C(f,n+h) W\left (\frac{n} {X} \right) W\left ( \frac{n + h}{ X} \right ) \sum_{\substack{0 \le h_1,h_2 \le y \\ h_2-h_1=h}} \left(1+O\left( \frac{y}{n}+\frac{y}{X} \right) \right) + O_f(1) \nonumber \\ &= \sum_{\lvert h\rvert \leq y} (y + 1 - \lvert h\rvert) \sum_{\substack{n \ge 1 }} \widetilde C(f,n) \widetilde C(f,n + h) W \left (\frac{n}{X} \right) W \left ( \frac{n + h}{X} \right ) +O_{f, \varepsilon}\left(y^3 X^{\varepsilon} \right). \end{align} $$
$$ \begin{align} &=\sum_{0 \leq h_1, h_2 \leq y} \sum_{\substack{n \ge 1 }} \widetilde C(f,n+h_1)\widetilde C(f,n+h_2) W\left(\frac{n}{X} \right)^2\nonumber \\ &= \sum_{\substack{\lvert h\rvert \leq y}} \sum_{\substack{n \ge 1}} \widetilde C(f,n) \widetilde C(f,n+h) W\left (\frac{n} {X} \right) W\left ( \frac{n + h}{ X} \right ) \sum_{\substack{0 \le h_1,h_2 \le y \\ h_2-h_1=h}} \left(1+O\left( \frac{y}{n}+\frac{y}{X} \right) \right) + O_f(1) \nonumber \\ &= \sum_{\lvert h\rvert \leq y} (y + 1 - \lvert h\rvert) \sum_{\substack{n \ge 1 }} \widetilde C(f,n) \widetilde C(f,n + h) W \left (\frac{n}{X} \right) W \left ( \frac{n + h}{X} \right ) +O_{f, \varepsilon}\left(y^3 X^{\varepsilon} \right). \end{align} $$
Using the bound (16) once again, we get that the term with
![]() $h=0$
in the sum on the right-hand side contributes
$h=0$
in the sum on the right-hand side contributes
 $$ \begin{align} \ll y \sum_{n \ge 1} \lvert c(f,n) \rvert^2 W \left ( \frac{n}{X} \right )^2 \ll_{f, \varepsilon} yX. \end{align} $$
$$ \begin{align} \ll y \sum_{n \ge 1} \lvert c(f,n) \rvert^2 W \left ( \frac{n}{X} \right )^2 \ll_{f, \varepsilon} yX. \end{align} $$
We next estimate the contribution from the terms in formula (25) with
![]() $h \neq 0$
. Recalling the definition of
$h \neq 0$
. Recalling the definition of
 $\mu ^2_{\leq Y}$
and using the fact that
$\mu ^2_{\leq Y}$
and using the fact that
 $$ \begin{align*} 1_{\left(n,2N\right)=1}=\sum_{\substack{d\mid\left(n,2N\right)}} \mu(d)=\sum_{\substack{d\mid 2N \\ d\mid n}} \mu(d), \end{align*} $$
$$ \begin{align*} 1_{\left(n,2N\right)=1}=\sum_{\substack{d\mid\left(n,2N\right)}} \mu(d)=\sum_{\substack{d\mid 2N \\ d\mid n}} \mu(d), \end{align*} $$
it follows that the contribution to the right-hand side of formula (25) from the terms with
![]() $h \neq 0$
is
$h \neq 0$
is
 $$ \begin{align} \ll y \sum_{\substack{0 < \lvert h\rvert \leq y \\ d_1, d_2 \leq Y \\ d_3,d_4 \mid 2N}} \left\lvert \sum_{\substack{d_1^2\mid n, d_2^2 \mid n + h \\ d_3\mid n, d_4\mid n+h}} c(f,n) c(f,n+h) W\left ( \frac{n}{X} \right ) W \left ( \frac{n + h}{X} \right ) \right\rvert. \end{align} $$
$$ \begin{align} \ll y \sum_{\substack{0 < \lvert h\rvert \leq y \\ d_1, d_2 \leq Y \\ d_3,d_4 \mid 2N}} \left\lvert \sum_{\substack{d_1^2\mid n, d_2^2 \mid n + h \\ d_3\mid n, d_4\mid n+h}} c(f,n) c(f,n+h) W\left ( \frac{n}{X} \right ) W \left ( \frac{n + h}{X} \right ) \right\rvert. \end{align} $$
For n with
![]() $d_1^2 \mid n$
,
$d_1^2 \mid n$
,
![]() $d_2^2 \mid n + h$
,
$d_2^2 \mid n + h$
,
![]() $d_3\mid n$
, and
$d_3\mid n$
, and
![]() $d_4\mid n+h$
, we have
$d_4\mid n+h$
, we have
![]() $n \equiv a \pmod {r}$
for some
$n \equiv a \pmod {r}$
for some
![]() $a,r \in \mathbb Z$
with
$a,r \in \mathbb Z$
with
![]() $ r\le 16 N^2 Y^4$
. Using additive characters to detect this congruence, we get that the inner sum in the previous expression is
$ r\le 16 N^2 Y^4$
. Using additive characters to detect this congruence, we get that the inner sum in the previous expression is
 $$ \begin{align*} & =\sum_{n \equiv a \! \! \! \! \pmod{r}} c(f,n) c(f,n+h) W \left ( \frac{n}{X} \right ) W \left ( \frac{n + h}{X} \right ) \\ &= \frac{1}{r} \sum_{0 \le v < r} e\left(\frac{-av}{r} \right) \sum_{n \ge 1} c(f,n) c(f,n+h)e \left ( \frac{n v}{r} \right ) W \left ( \frac{n}{X} \right ) W \left ( \frac{n + h}{X} \right ). \end{align*} $$
$$ \begin{align*} & =\sum_{n \equiv a \! \! \! \! \pmod{r}} c(f,n) c(f,n+h) W \left ( \frac{n}{X} \right ) W \left ( \frac{n + h}{X} \right ) \\ &= \frac{1}{r} \sum_{0 \le v < r} e\left(\frac{-av}{r} \right) \sum_{n \ge 1} c(f,n) c(f,n+h)e \left ( \frac{n v}{r} \right ) W \left ( \frac{n}{X} \right ) W \left ( \frac{n + h}{X} \right ). \end{align*} $$
For
![]() $v \neq 0$
write
$v \neq 0$
write
![]() $v/r=v'/r'$
, with
$v/r=v'/r'$
, with
![]() $(r',v')=1$
, and if
$(r',v')=1$
, and if
![]() $v=0$
, set
$v=0$
, set
![]() $r'=1$
. Applying Proposition 3.5, this sum is
$r'=1$
. Applying Proposition 3.5, this sum is
 $\ll _{f, \varepsilon } X^{1-\frac {1}{102}+\varepsilon }$
, provided that
$\ll _{f, \varepsilon } X^{1-\frac {1}{102}+\varepsilon }$
, provided that
![]() $r' \le X^{\frac {1}{102}}$
and
$r' \le X^{\frac {1}{102}}$
and
 $0<\lvert h\rvert < X^{\frac {1}{2}}$
. Hence, by this along with the bound (26) we conclude that for
$0<\lvert h\rvert < X^{\frac {1}{2}}$
. Hence, by this along with the bound (26) we conclude that for
![]() $16N^2 Y^4 \le X^{\frac {1}{102}}$
, the right-hand side of formula (25) is
$16N^2 Y^4 \le X^{\frac {1}{102}}$
, the right-hand side of formula (25) is
 $ \ll _{f, \varepsilon } y X+ y^2 Y^2 X^{1-\frac {1}{102}+\varepsilon }+y^3 X^{\varepsilon }, $
which is
$ \ll _{f, \varepsilon } y X+ y^2 Y^2 X^{1-\frac {1}{102}+\varepsilon }+y^3 X^{\varepsilon }, $
which is
![]() $\ll y X$
, as needed, provided that
$\ll y X$
, as needed, provided that
![]() $y \le X^{1/4}$
and
$y \le X^{1/4}$
and
 $$ \begin{align} yY^2X^{\varepsilon} \ll X^{\frac{1}{102}}. \end{align} $$
$$ \begin{align} yY^2X^{\varepsilon} \ll X^{\frac{1}{102}}. \end{align} $$
It remains to optimize our parameters. Recall that to handle the contribution of the small divisors, we required
![]() $Y \ge \sqrt {y} X^{\varepsilon }$
. We now choose
$Y \ge \sqrt {y} X^{\varepsilon }$
. We now choose
![]() $Y=\sqrt {y} X^{\varepsilon }$
. Taking the constraint (28) into account, the largest we can choose y is
$Y=\sqrt {y} X^{\varepsilon }$
. Taking the constraint (28) into account, the largest we can choose y is
 $y=X^{\frac {1}{204}-\frac {3}{2}\varepsilon }$
. We conclude by noting that with these choices, we have
$y=X^{\frac {1}{204}-\frac {3}{2}\varepsilon }$
. We conclude by noting that with these choices, we have
![]() $16 N^2 Y^4 \ll _N X^{\frac {1}{102}-3\varepsilon } \le X^{\frac {1}{102}}$
, as required for the application of Proposition 3.5.□
$16 N^2 Y^4 \ll _N X^{\frac {1}{102}-3\varepsilon } \le X^{\frac {1}{102}}$
, as required for the application of Proposition 3.5.□
4. Large values for coefficients of half-integral-weight forms
The main result of this section, Theorem 4.1, generalizes [Reference Gun and Sengupta21, Theorem 1] (which treated the case
![]() $N=1$
).
$N=1$
).
4.1. Statement of main result
Theorem 4.1. Let
![]() $k \ge 2$
be an integer,
$k \ge 2$
be an integer,
![]() $N \ge 1$
be odd and square-free, and
$N \ge 1$
be odd and square-free, and
 $h \in S_{k+\frac 12}^+(4N)$
be a cusp form. Let
$h \in S_{k+\frac 12}^+(4N)$
be a cusp form. Let
![]() $\varepsilon>0$
be fixed. Then for all X sufficiently large, there exist at least
$\varepsilon>0$
be fixed. Then for all X sufficiently large, there exist at least
![]() $X^{1-\varepsilon }$
odd square-free integers n coprime to N such that
$X^{1-\varepsilon }$
odd square-free integers n coprime to N such that
![]() $X \le n \le 2X$
and
$X \le n \le 2X$
and
 $$ \begin{align*} \lvert c(h,n)\rvert \ge \exp\left(\frac{1}{82} \sqrt{\frac{\log n}{\log \log n}} \right). \end{align*} $$
$$ \begin{align*} \lvert c(h,n)\rvert \ge \exp\left(\frac{1}{82} \sqrt{\frac{\log n}{\log \log n}} \right). \end{align*} $$
We will prove this theorem by combining methods of [Reference Gun and Sengupta21] and [Reference Lester and Radziwiłł39, Reference Resnikoff and Saldana50]. Our first job is to reduce the question to bounding central values of L-functions. This is done by using the explicit form of Waldspurger’s formula due to Kohnen (Proposition 2.2).
4.2. Reduction to bounds on L-values
Fix an integer
![]() $k \ge 2$
and an odd square-free integer
$k \ge 2$
and an odd square-free integer
![]() $N\geq 1$
throughout §
$N\geq 1$
throughout §
![]() $4$
. Let h be as in Theorem 4.1. We use the basis (13) to write
$4$
. Let h be as in Theorem 4.1. We use the basis (13) to write
 $$ \begin{align*} h = \sum_{\substack{r,\ell\geq 1\\ r\ell\mid N}}\sum_{f\in{\mathcal B}_{k+\frac12,4\ell}^{\text{new}}} \alpha_{r,\ell, f} f\mid U\left(r^2\right), \end{align*} $$
$$ \begin{align*} h = \sum_{\substack{r,\ell\geq 1\\ r\ell\mid N}}\sum_{f\in{\mathcal B}_{k+\frac12,4\ell}^{\text{new}}} \alpha_{r,\ell, f} f\mid U\left(r^2\right), \end{align*} $$
where the coefficients
![]() $\alpha _{r, \ell , f}$
depend only on
$\alpha _{r, \ell , f}$
depend only on
![]() $r, \ell , f, h$
. For each odd square-free n, we use Lemma 2.1 to get the following identity for the Fourier coefficients:
$r, \ell , f, h$
. For each odd square-free n, we use Lemma 2.1 to get the following identity for the Fourier coefficients:
 $$ \begin{align*} c(h,n)= \sum_{\ell\mid N}\sum_{f\in{\mathcal B}_{k+\frac12,4\ell}^{\text{new}}} c(f,n) \sum_{r\mid \frac{N}{\ell}}\alpha_{r,\ell,f} \prod_{p\mid r}\left(\lambda_f(p) - \frac{1}{\sqrt{p}}\left(\frac{(-1)^kn}{p} \right) \right). \end{align*} $$
$$ \begin{align*} c(h,n)= \sum_{\ell\mid N}\sum_{f\in{\mathcal B}_{k+\frac12,4\ell}^{\text{new}}} c(f,n) \sum_{r\mid \frac{N}{\ell}}\alpha_{r,\ell,f} \prod_{p\mid r}\left(\lambda_f(p) - \frac{1}{\sqrt{p}}\left(\frac{(-1)^kn}{p} \right) \right). \end{align*} $$
We already know that
![]() $c(h,n) \neq 0$
for some odd square-free n (this follows from [Reference Schmidt58], for example). So there exist
$c(h,n) \neq 0$
for some odd square-free n (this follows from [Reference Schmidt58], for example). So there exist
![]() $\ell _0\mid N$
,
$\ell _0\mid N$
,
 $f_0\in {\mathcal B}_{k+\frac 12,4\ell _0}^{\mathrm {new}}$
, and a reduced residue class
$f_0\in {\mathcal B}_{k+\frac 12,4\ell _0}^{\mathrm {new}}$
, and a reduced residue class
![]() $\eta \bmod 4N$
such that
$\eta \bmod 4N$
such that
 $$ \begin{align*} \eta \equiv 1 \pmod{4}, \qquad \left(\frac{\eta}p\right)=w_p \quad \text{ for each } p\mid\ell_0, \\ \sum_{r\mid \frac{N}{\ell_0}}\alpha_{r,\ell_0,f_0} \prod_{p\mid r}\left(\lambda_{f_0}(p) - \frac{1}{\sqrt{p}}\left(\frac{\eta}{p} \right) \right) \neq 0. \end{align*} $$
$$ \begin{align*} \eta \equiv 1 \pmod{4}, \qquad \left(\frac{\eta}p\right)=w_p \quad \text{ for each } p\mid\ell_0, \\ \sum_{r\mid \frac{N}{\ell_0}}\alpha_{r,\ell_0,f_0} \prod_{p\mid r}\left(\lambda_{f_0}(p) - \frac{1}{\sqrt{p}}\left(\frac{\eta}{p} \right) \right) \neq 0. \end{align*} $$
Here,
![]() $w_p$
is the eigenvalue of the Atkin–Lehner operator
$w_p$
is the eigenvalue of the Atkin–Lehner operator
![]() $W_p$
acting on
$W_p$
acting on
![]() $f_0$
. For brevity, we denote, for each
$f_0$
. For brevity, we denote, for each
 $f \in {\mathcal B}_{k+\frac 12,4\ell }^{\mathrm {new}}$
,
$f \in {\mathcal B}_{k+\frac 12,4\ell }^{\mathrm {new}}$
,
 $$ \begin{align*} \beta_{f} = \sum_{r\mid \frac{N}{\ell}}\alpha_{r,\ell,f} \prod_{p\mid r}\left(\lambda_{f}(p) - \frac{1}{\sqrt{p}}\left(\frac{\eta}{p} \right) \right). \end{align*} $$
$$ \begin{align*} \beta_{f} = \sum_{r\mid \frac{N}{\ell}}\alpha_{r,\ell,f} \prod_{p\mid r}\left(\lambda_{f}(p) - \frac{1}{\sqrt{p}}\left(\frac{\eta}{p} \right) \right). \end{align*} $$
We will denote the Shimura lift of
 $f\in {\mathcal B}_{k+\frac 12,4\ell }^{\mathrm {new}}$
by
$f\in {\mathcal B}_{k+\frac 12,4\ell }^{\mathrm {new}}$
by
![]() $g_{f}\in S_{2k}^{\mathrm {new}}(\ell )$
with Fourier coefficients
$g_{f}\in S_{2k}^{\mathrm {new}}(\ell )$
with Fourier coefficients
 $m^{k - \frac 12}\lambda _{g_f}(m)$
normalized so that
$m^{k - \frac 12}\lambda _{g_f}(m)$
normalized so that
![]() $\lambda _{g_f}(1)=1$
. Also, write
$\lambda _{g_f}(1)=1$
. Also, write
![]() $g_0$
for
$g_0$
for
![]() $g_{f_0}$
and
$g_{f_0}$
and
 $m^{k-\frac 12}\lambda _0(m)$
for its Fourier coefficients. For each odd, square-free integer n such that
$m^{k-\frac 12}\lambda _0(m)$
for its Fourier coefficients. For each odd, square-free integer n such that
![]() $d=(-1)^k n \equiv \eta \pmod 4N$
, we use the triangle inequality, Cauchy–Schwarz, and Proposition 2.2 to obtain
$d=(-1)^k n \equiv \eta \pmod 4N$
, we use the triangle inequality, Cauchy–Schwarz, and Proposition 2.2 to obtain
 $$ \begin{align} \lvert c(h, n)\rvert &= \left\lvert\sum_{\ell\mid N}\sum_{f\in{\mathcal B}_{k+\frac12,4\ell}^{\text{new}}} c(f,n) \beta_f\right\rvert \nonumber\\ & \ge \left\lvert\beta_{f_0} c_{f_0}(n)\right\rvert -\sqrt{\left(\sum_{\ell\mid N}\sum_{f_0 \ne f\in{\mathcal B}_{k+\frac12,4\ell}^{\text{new}}} \lvert c(f,n) \rvert^2 \right) \left(\sum_{\ell\mid N}\sum_{f_0 \ne f\in{\mathcal B}_{k+\frac12,4\ell}^{\text{new}}} \left\lvert \beta_f\right\rvert^2 \right)} \nonumber \\ & \ge A \sqrt{L\left(\frac12,g_0\otimes\chi_d\right)} - B \sqrt{\sum_{\ell\mid N}\sum_{f_0 \ne f\in{\mathcal B}_{k+\frac12,4\ell}^{\text{new}}} L\left(\frac12,g_f\otimes\chi_d\right)}, \end{align} $$
$$ \begin{align} \lvert c(h, n)\rvert &= \left\lvert\sum_{\ell\mid N}\sum_{f\in{\mathcal B}_{k+\frac12,4\ell}^{\text{new}}} c(f,n) \beta_f\right\rvert \nonumber\\ & \ge \left\lvert\beta_{f_0} c_{f_0}(n)\right\rvert -\sqrt{\left(\sum_{\ell\mid N}\sum_{f_0 \ne f\in{\mathcal B}_{k+\frac12,4\ell}^{\text{new}}} \lvert c(f,n) \rvert^2 \right) \left(\sum_{\ell\mid N}\sum_{f_0 \ne f\in{\mathcal B}_{k+\frac12,4\ell}^{\text{new}}} \left\lvert \beta_f\right\rvert^2 \right)} \nonumber \\ & \ge A \sqrt{L\left(\frac12,g_0\otimes\chi_d\right)} - B \sqrt{\sum_{\ell\mid N}\sum_{f_0 \ne f\in{\mathcal B}_{k+\frac12,4\ell}^{\text{new}}} L\left(\frac12,g_f\otimes\chi_d\right)}, \end{align} $$
where
![]() $A>0$
and
$A>0$
and
![]() $B>0$
are independent of d. Now Theorem 4.1 follows from the following auxiliary result:
$B>0$
are independent of d. Now Theorem 4.1 follows from the following auxiliary result:
Proposition 4.2. Let
![]() $C\ge 0$
be a constant,
$C\ge 0$
be a constant,
![]() $\varepsilon>0$
, and let
$\varepsilon>0$
, and let
![]() $\eta \pmod {4N}$
be a fixed reduced residue class with
$\eta \pmod {4N}$
be a fixed reduced residue class with
![]() $\eta \equiv 1 \pmod 4$
. Given
$\eta \equiv 1 \pmod 4$
. Given
![]() $\ell _0\mid N$
, let
$\ell _0\mid N$
, let
 $f_0 \in {\mathcal B}_{k+\frac 12,4\ell _0}^{\mathrm {new}}$
be a newform as before with Shimura lift
$f_0 \in {\mathcal B}_{k+\frac 12,4\ell _0}^{\mathrm {new}}$
be a newform as before with Shimura lift
![]() $g_0$
. For sufficiently large X, there are
$g_0$
. For sufficiently large X, there are
![]() $\ge X^{1-\varepsilon }$
odd square-free integers
$\ge X^{1-\varepsilon }$
odd square-free integers
![]() $n \in [X, 2X]$
, such that
$n \in [X, 2X]$
, such that
![]() $d=(-1)^kn\equiv \eta \pmod {4N}$
and
$d=(-1)^kn\equiv \eta \pmod {4N}$
and
 $$ \begin{align} L\left(\tfrac12,g_0\otimes\chi_d\right)>C\sum_{\ell\mid N}\sum_{\substack{f\in{\mathcal B}_{k+\frac12,4\ell}^{\mathrm{new}}\\ \left(\ell,f\right)\neq\left(\ell_0,f_0\right)}}L\left(\tfrac12,g_f\otimes\chi_d\right)+ \exp\left(\frac1{40}\sqrt{\frac{\log X}{\log\log X}}\right). \end{align} $$
$$ \begin{align} L\left(\tfrac12,g_0\otimes\chi_d\right)>C\sum_{\ell\mid N}\sum_{\substack{f\in{\mathcal B}_{k+\frac12,4\ell}^{\mathrm{new}}\\ \left(\ell,f\right)\neq\left(\ell_0,f_0\right)}}L\left(\tfrac12,g_f\otimes\chi_d\right)+ \exp\left(\frac1{40}\sqrt{\frac{\log X}{\log\log X}}\right). \end{align} $$
We first explain how Proposition 4.2 implies Theorem 4.1. Put
 $L_0 = L\left (\frac 12,g_0\otimes \chi _d\right )$
and
$L_0 = L\left (\frac 12,g_0\otimes \chi _d\right )$
and
 $L_1 = \sum _{\ell \mid N}\sum _{f_0 \ne f\in {\mathcal B}_{k+\frac 12,4\ell }^{\mathrm {new}}}L\left (\frac 12,g_f\otimes \chi _d\right )$
. Put
$L_1 = \sum _{\ell \mid N}\sum _{f_0 \ne f\in {\mathcal B}_{k+\frac 12,4\ell }^{\mathrm {new}}}L\left (\frac 12,g_f\otimes \chi _d\right )$
. Put
![]() $C=2B^2/A^2$
. Combining Proposition 4.2 and the estimate (29),
$C=2B^2/A^2$
. Combining Proposition 4.2 and the estimate (29),
 $$ \begin{align*} \lvert c(h, n)\rvert &\ge A \sqrt{L_0} - B \sqrt{L_1}> A \sqrt{CL_1 + \exp\left(\frac1{40}\sqrt{\frac{\log X}{\log\log X}}\right)} - B \sqrt{L_1} \\ & \ge \frac{A}{\sqrt{2}}\left(\sqrt{CL_1} + \exp\left(\frac1{80}\sqrt{\frac{\log X}{\log\log X}}\right)\right) - B \sqrt{L_1}\\ &= \frac{A}{\sqrt{2}} \exp\left(\frac1{80}\sqrt{\frac{\log X}{\log\log X}}\right) \ge \exp\left(\frac{1}{82} \sqrt{\frac{\log n}{\log \log n}} \right) \end{align*} $$
$$ \begin{align*} \lvert c(h, n)\rvert &\ge A \sqrt{L_0} - B \sqrt{L_1}> A \sqrt{CL_1 + \exp\left(\frac1{40}\sqrt{\frac{\log X}{\log\log X}}\right)} - B \sqrt{L_1} \\ & \ge \frac{A}{\sqrt{2}}\left(\sqrt{CL_1} + \exp\left(\frac1{80}\sqrt{\frac{\log X}{\log\log X}}\right)\right) - B \sqrt{L_1}\\ &= \frac{A}{\sqrt{2}} \exp\left(\frac1{80}\sqrt{\frac{\log X}{\log\log X}}\right) \ge \exp\left(\frac{1}{82} \sqrt{\frac{\log n}{\log \log n}} \right) \end{align*} $$
for sufficiently large X. We now proceed with the proof of Proposition 4.2. For
![]() $\eta \equiv 1 \pmod 4$
, let
$\eta \equiv 1 \pmod 4$
, let
 $$ \begin{align*} \mathcal D_{N,\eta}=\left\{d=(-1)^kn : \mu^2(2n)\neq 0,\,(n,N)=1,\, d\equiv \eta\! \! \! \! \pmod {4N}\right\} \end{align*} $$
$$ \begin{align*} \mathcal D_{N,\eta}=\left\{d=(-1)^kn : \mu^2(2n)\neq 0,\,(n,N)=1,\, d\equiv \eta\! \! \! \! \pmod {4N}\right\} \end{align*} $$
and
For each such d we introduce a resonance polynomial
 $$ \begin{align*} R(d)=\sum_{m\leq M}r(m)\lambda_0(m)\chi_d(m), \end{align*} $$
$$ \begin{align*} R(d)=\sum_{m\leq M}r(m)\lambda_0(m)\chi_d(m), \end{align*} $$
where the coefficients
![]() $r(m)$
are multiplicative and supported on square-free integers. At primes we set
$r(m)$
are multiplicative and supported on square-free integers. At primes we set
 $$ \begin{align*} r(p)=\begin{cases} \frac L{\sqrt p \log p}&\text{if }L^2\leq p\leq L^4\text{ and }p\nmid N \\ 0&\text{otherwise}, \end{cases} \end{align*} $$
$$ \begin{align*} r(p)=\begin{cases} \frac L{\sqrt p \log p}&\text{if }L^2\leq p\leq L^4\text{ and }p\nmid N \\ 0&\text{otherwise}, \end{cases} \end{align*} $$
where
 $L=\frac 18\sqrt {\log M\log \log M}$
, with
$L=\frac 18\sqrt {\log M\log \log M}$
, with
![]() $M=X^{1/24}$
.
$M=X^{1/24}$
.
The strategy to prove the estimate (30) is to consider the quantity
 $$ \begin{align*} \sum_{d\in\mathcal D_{N,\eta}(X)}L\left(\tfrac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2. \end{align*} $$
$$ \begin{align*} \sum_{d\in\mathcal D_{N,\eta}(X)}L\left(\tfrac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2. \end{align*} $$
Let
![]() $\mathcal S$
be the subset of
$\mathcal S$
be the subset of
![]() $\mathcal D_{N,\eta }(X)$
for which the estimate (30) holds. Then certainly
$\mathcal D_{N,\eta }(X)$
for which the estimate (30) holds. Then certainly
 $$ \begin{align*} & \sum_{d\in\mathcal D_{N,\eta}(X)} L\left(\frac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2\\ &\quad \leq\sum_{d\in\mathcal D_{N,\eta}(X)}\left(\sum_{\substack{\ell=1\\ \ell\mid N}}^\infty\sum_{\substack{f\in{\mathcal B}_{k+\frac12,4\ell}^{\mathrm{new}}\\ \left(\ell,f\right)\neq\left(\ell_0,f_0\right)}}CL\left(\frac12,g_f\otimes\chi_d\right)+\exp\left(\frac1{40}\sqrt{\frac{\log X}{\log\log X}}\right)\right)\lvert R(d)\rvert^2\\ &\qquad+\sum_{d\in\mathcal S}L\left(\frac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2. \end{align*} $$
$$ \begin{align*} & \sum_{d\in\mathcal D_{N,\eta}(X)} L\left(\frac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2\\ &\quad \leq\sum_{d\in\mathcal D_{N,\eta}(X)}\left(\sum_{\substack{\ell=1\\ \ell\mid N}}^\infty\sum_{\substack{f\in{\mathcal B}_{k+\frac12,4\ell}^{\mathrm{new}}\\ \left(\ell,f\right)\neq\left(\ell_0,f_0\right)}}CL\left(\frac12,g_f\otimes\chi_d\right)+\exp\left(\frac1{40}\sqrt{\frac{\log X}{\log\log X}}\right)\right)\lvert R(d)\rvert^2\\ &\qquad+\sum_{d\in\mathcal S}L\left(\frac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2. \end{align*} $$
Suppose that the following estimates hold:
 $$ \begin{align} \sum_{d\in\mathcal D_{N,\eta}(X)} & L\left(\tfrac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2\gg_{k,N} X\cdot\mathcal R\cdot\exp\left(\left(\frac12+o(1)\right)\frac L{\log L}\right), \end{align} $$
$$ \begin{align} \sum_{d\in\mathcal D_{N,\eta}(X)} & L\left(\tfrac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2\gg_{k,N} X\cdot\mathcal R\cdot\exp\left(\left(\frac12+o(1)\right)\frac L{\log L}\right), \end{align} $$
 $$ \begin{align} \sum_{d\in\mathcal D_{N,\eta}(X)} & L\left(\tfrac12,g_f\otimes\chi_d\right)\lvert R(d)\rvert^2\ll_{k,N} X\cdot\mathcal R\cdot\exp\left(o\left(\frac L{\log L}\right)\right) \qquad \text{for}\ f\neq f_0, \end{align} $$
$$ \begin{align} \sum_{d\in\mathcal D_{N,\eta}(X)} & L\left(\tfrac12,g_f\otimes\chi_d\right)\lvert R(d)\rvert^2\ll_{k,N} X\cdot\mathcal R\cdot\exp\left(o\left(\frac L{\log L}\right)\right) \qquad \text{for}\ f\neq f_0, \end{align} $$
 $$ \begin{align} \sum_{d\in\mathcal D_{N,\eta}(X)} & \lvert R(d)\rvert^2\leq\frac{2X}{\pi^2}\cdot\mathcal R+O(X), \end{align} $$
$$ \begin{align} \sum_{d\in\mathcal D_{N,\eta}(X)} & \lvert R(d)\rvert^2\leq\frac{2X}{\pi^2}\cdot\mathcal R+O(X), \end{align} $$
 $$ \begin{align} \sum_{d\in\mathcal D_{N,\eta}(X)} & \lvert R(d)\rvert^6\ll X\cdot\exp\left(O\left(\frac{\log X}{\log\log X}\right)\right), \end{align} $$
$$ \begin{align} \sum_{d\in\mathcal D_{N,\eta}(X)} & \lvert R(d)\rvert^6\ll X\cdot\exp\left(O\left(\frac{\log X}{\log\log X}\right)\right), \end{align} $$
where
 $$ \begin{align*} \mathcal R=\prod_{L^2\leq p\leq L^4}\left(1+r(p)^2\lambda_0(p)^2\right). \end{align*} $$
$$ \begin{align*} \mathcal R=\prod_{L^2\leq p\leq L^4}\left(1+r(p)^2\lambda_0(p)^2\right). \end{align*} $$
Assuming the estimates (31)–(34), the proof of Proposition 4.2 can be finished as follows. We observe that
 $$ \begin{align*} X\cdot\mathcal R\cdot\exp\left(\left(\frac12+o(1)\right)\frac L{\log L}\right)&\ll_{k,N}\sum_{d\in\mathcal D_{N,\eta}(X)}L\left(\tfrac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2\\ &\ll_{k,N} X\cdot\mathcal R\cdot\exp\left(o\left(\frac L{\log L}\right)\right)+\sum_{d\in\mathcal S}L\left(\tfrac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2 \end{align*} $$
$$ \begin{align*} X\cdot\mathcal R\cdot\exp\left(\left(\frac12+o(1)\right)\frac L{\log L}\right)&\ll_{k,N}\sum_{d\in\mathcal D_{N,\eta}(X)}L\left(\tfrac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2\\ &\ll_{k,N} X\cdot\mathcal R\cdot\exp\left(o\left(\frac L{\log L}\right)\right)+\sum_{d\in\mathcal S}L\left(\tfrac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2 \end{align*} $$
by using the estimates (31)–(33). Hence
 $$ \begin{align} X\cdot\mathcal R\cdot\exp\left(\left(\frac12+o(1)\right)\frac L{\log L}\right)\ll_{k,N} \sum_{d\in\mathcal S}L\left(\tfrac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2. \end{align} $$
$$ \begin{align} X\cdot\mathcal R\cdot\exp\left(\left(\frac12+o(1)\right)\frac L{\log L}\right)\ll_{k,N} \sum_{d\in\mathcal S}L\left(\tfrac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2. \end{align} $$
On the other hand, the right-hand side can be estimated by Hölder’s inequality and the estimate (34) as
 $$ \begin{align*} &\leq \left(\sum_{d\in\mathcal D_{N,\eta}(X)}L\left(\tfrac12,g_0\otimes\chi_d\right)^2\right)^{1/2}\cdot \lvert \mathcal S\rvert^{1/6}\left(\sum_{d\in\mathcal S}\lvert R(d)\rvert^6\right)^{1/3}\\ &\ll_{k,N} X^{1/2+\varepsilon/2}\lvert\mathcal S\rvert^{1/6}\cdot\left(X\cdot\exp\left(O\left(\frac{\log X}{\log\log X}\right)\right)\right)^{1/3}, \end{align*} $$
$$ \begin{align*} &\leq \left(\sum_{d\in\mathcal D_{N,\eta}(X)}L\left(\tfrac12,g_0\otimes\chi_d\right)^2\right)^{1/2}\cdot \lvert \mathcal S\rvert^{1/6}\left(\sum_{d\in\mathcal S}\lvert R(d)\rvert^6\right)^{1/3}\\ &\ll_{k,N} X^{1/2+\varepsilon/2}\lvert\mathcal S\rvert^{1/6}\cdot\left(X\cdot\exp\left(O\left(\frac{\log X}{\log\log X}\right)\right)\right)^{1/3}, \end{align*} $$
where, as before, the average of the squares of central L-values is estimated by using the quadratic large sieve of Heath-Brown [Reference Henniart25] (here we can extend the sum to all fundamental discriminants
![]() $\le X$
in magnitude by nonnegativity). Combining this with the estimate (35) gives
$\le X$
in magnitude by nonnegativity). Combining this with the estimate (35) gives
![]() $\lvert \mathcal S\rvert \gg _{k,N} X^{1-\varepsilon /2} \ge X^{1-\varepsilon }$
, as desired.
$\lvert \mathcal S\rvert \gg _{k,N} X^{1-\varepsilon /2} \ge X^{1-\varepsilon }$
, as desired.
So it suffices to establish estimates (31)–(34). Notice that the estimates (33) and (34) follow directly from [Reference Gun and Sengupta21, Proposition 3] by simply estimating
 $$ \begin{align*} \sum_{d\in\mathcal D_{N,\eta}(X)}\lvert R(d)\rvert^2 & \leq\sum_{\substack{X\leq (-1)^kd\leq 2X\\ d\equiv 1 \! \! \! \! \pmod{4}}}\lvert R(d)\rvert^2\qquad\text{and}\qquad \\ \sum_{d\in\mathcal D_{N,\eta}(X)}\lvert R(d)\rvert^6 &\leq\sum_{\substack{X\leq (-1)^kd\leq 2X\\ d\equiv 1\! \! \! \! \pmod{4}}}\lvert R(d)\rvert^6. \end{align*} $$
$$ \begin{align*} \sum_{d\in\mathcal D_{N,\eta}(X)}\lvert R(d)\rvert^2 & \leq\sum_{\substack{X\leq (-1)^kd\leq 2X\\ d\equiv 1 \! \! \! \! \pmod{4}}}\lvert R(d)\rvert^2\qquad\text{and}\qquad \\ \sum_{d\in\mathcal D_{N,\eta}(X)}\lvert R(d)\rvert^6 &\leq\sum_{\substack{X\leq (-1)^kd\leq 2X\\ d\equiv 1\! \! \! \! \pmod{4}}}\lvert R(d)\rvert^6. \end{align*} $$
The other two estimates are consequences of the following first moment result.
Proposition 4.3. Let
![]() $N\geq 1$
be a positive integer and let
$N\geq 1$
be a positive integer and let
![]() $g\in S_{2k}^{\mathrm {new}}(\ell )$
for some
$g\in S_{2k}^{\mathrm {new}}(\ell )$
for some
![]() $\ell \mid N$
. Suppose that u is an odd positive integer coprime to N and write
$\ell \mid N$
. Suppose that u is an odd positive integer coprime to N and write
![]() $u=u_1u_2^2$
, with
$u=u_1u_2^2$
, with
![]() $u_1$
square-free. Let
$u_1$
square-free. Let
![]() $\Phi $
denote a smooth and compactly supported function in
$\Phi $
denote a smooth and compactly supported function in
![]() $[1/2,5/2]$
. Then
$[1/2,5/2]$
. Then
 $$ \begin{align*} &\sum_{d\in \mathcal D_{N,\eta}}L\left(\tfrac12,g\otimes\chi_d\right)\chi_d(u)\Phi\left(\frac{\lvert d\rvert}X\right)\\ &\quad=\frac{X\lambda_g(u_1)}{2Nu_1^{1/2}}\left(\int_0^\infty\Phi(\xi)\mathrm d \xi\right)L_{g,\eta}\left(\tfrac12\right)L\left(1,\mathrm{Sym}^2g\right)\mathcal G(1;u)+O_{k,N, \Phi, \varepsilon}\left(X^{7/8+\varepsilon}u^{3/8+\varepsilon}\right). \end{align*} $$
$$ \begin{align*} &\sum_{d\in \mathcal D_{N,\eta}}L\left(\tfrac12,g\otimes\chi_d\right)\chi_d(u)\Phi\left(\frac{\lvert d\rvert}X\right)\\ &\quad=\frac{X\lambda_g(u_1)}{2Nu_1^{1/2}}\left(\int_0^\infty\Phi(\xi)\mathrm d \xi\right)L_{g,\eta}\left(\tfrac12\right)L\left(1,\mathrm{Sym}^2g\right)\mathcal G(1;u)+O_{k,N, \Phi, \varepsilon}\left(X^{7/8+\varepsilon}u^{3/8+\varepsilon}\right). \end{align*} $$
Here
![]() $L_{g,\eta }(1/2)\neq 0$
is the Dirichlet series given in equation (36) and
$L_{g,\eta }(1/2)\neq 0$
is the Dirichlet series given in equation (36) and
![]() $\mathcal G(1;u)$
is the Euler product defined in equation (41). Furthermore,
$\mathcal G(1;u)$
is the Euler product defined in equation (41). Furthermore,
![]() $\mathcal G(1;\cdot )$
is a multiplicative function satisfying
$\mathcal G(1;\cdot )$
is a multiplicative function satisfying
 $\mathcal G\left (1;p^k\right )=1+O(1/p)$
at prime powers.
$\mathcal G\left (1;p^k\right )=1+O(1/p)$
at prime powers.
4.3. A twisted first moment asymptotic
In this subsection, we sketch the proof of Proposition 4.3. The starting point is the approximate functional equation (which follows by an easy modification of the proof of [Reference Resnikoff and Saldana50, Lemma 5]) saying that
 $$ \begin{align*} L\left(\frac12,g\otimes\chi_d\right)=2\sum_{\substack{m=1\\ \left(m,2N\right)=1}}^\infty\frac{\lambda_g(m)\chi_d(m)}{\sqrt m}W_{g,\eta}\left(\frac m{\lvert d\rvert}\right), \end{align*} $$
$$ \begin{align*} L\left(\frac12,g\otimes\chi_d\right)=2\sum_{\substack{m=1\\ \left(m,2N\right)=1}}^\infty\frac{\lambda_g(m)\chi_d(m)}{\sqrt m}W_{g,\eta}\left(\frac m{\lvert d\rvert}\right), \end{align*} $$
where
![]() $W_{g,\eta }$
is a smooth weight function defined by, for
$W_{g,\eta }$
is a smooth weight function defined by, for
![]() $c>1/2$
,
$c>1/2$
,
 $$ \begin{align} W_{g,\eta}(\xi)=\frac1{2\pi i}\int_{(c)}L_{g,\eta}\!\left( \! s+\frac12 \!\right)\!\frac{\Gamma(s+k)}{\Gamma(k)}\!{\left(\!\frac{\sqrt \ell}{2\pi\xi}\!\right)\!}^s \frac{\mathrm d s}s, \quad L_{g,\eta}(s)=\sum_{\substack{m=1\\ p\mid m\implies p\mid 2N}}^\infty\frac{\lambda_g(m)\chi_d(m)}{m^s}. \end{align} $$
$$ \begin{align} W_{g,\eta}(\xi)=\frac1{2\pi i}\int_{(c)}L_{g,\eta}\!\left( \! s+\frac12 \!\right)\!\frac{\Gamma(s+k)}{\Gamma(k)}\!{\left(\!\frac{\sqrt \ell}{2\pi\xi}\!\right)\!}^s \frac{\mathrm d s}s, \quad L_{g,\eta}(s)=\sum_{\substack{m=1\\ p\mid m\implies p\mid 2N}}^\infty\frac{\lambda_g(m)\chi_d(m)}{m^s}. \end{align} $$
Notice that the value of
![]() $L_{g,\eta }(s)$
is the same for each
$L_{g,\eta }(s)$
is the same for each
![]() $d\equiv \eta \pmod {4N}$
. The weight function satisfies
$d\equiv \eta \pmod {4N}$
. The weight function satisfies
 $W_{g,\eta }(\xi )=L_{g,\eta }(1/2)+O_{k,N,\varepsilon }\left (\xi ^{\frac 12-\varepsilon }\right )$
as
$W_{g,\eta }(\xi )=L_{g,\eta }(1/2)+O_{k,N,\varepsilon }\left (\xi ^{\frac 12-\varepsilon }\right )$
as
![]() $\xi \longrightarrow 0$
and
$\xi \longrightarrow 0$
and
![]() $W_{g,\eta }(\xi )\ll _{k,N,A}\lvert \xi \rvert ^{-A}$
for any
$W_{g,\eta }(\xi )\ll _{k,N,A}\lvert \xi \rvert ^{-A}$
for any
![]() $A\geq 1$
as
$A\geq 1$
as
![]() $\xi \longrightarrow \infty $
. Thus the sum we have to evaluate takes the shape
$\xi \longrightarrow \infty $
. Thus the sum we have to evaluate takes the shape
 $$ \begin{align} 2\sum_{\substack{m=1\\ \left(m,2N\right)=1}}^\infty\frac{\lambda_g(m)}{\sqrt m}\sum_{d\in\mathcal D_{N,\eta}}\chi_d(mu)W_{g,\eta}\left(\frac m{\lvert d\rvert}\right)\Phi\left(\frac{\lvert d\rvert}X\right). \end{align} $$
$$ \begin{align} 2\sum_{\substack{m=1\\ \left(m,2N\right)=1}}^\infty\frac{\lambda_g(m)}{\sqrt m}\sum_{d\in\mathcal D_{N,\eta}}\chi_d(mu)W_{g,\eta}\left(\frac m{\lvert d\rvert}\right)\Phi\left(\frac{\lvert d\rvert}X\right). \end{align} $$
Notice that by definition, any
![]() $d\in \mathcal D_{N,\eta }$
is square-free and odd. We pick out this property by the identity
$d\in \mathcal D_{N,\eta }$
is square-free and odd. We pick out this property by the identity
 $$ \begin{align} \sum_{\substack{\alpha=1\\ \left(\alpha,2N\right)=1\\ \alpha^2\mid d}}^\infty\mu(\alpha)=\begin{cases} 1 & \text{if }d\text{ is square-free},\\ 0 & \text{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} \sum_{\substack{\alpha=1\\ \left(\alpha,2N\right)=1\\ \alpha^2\mid d}}^\infty\mu(\alpha)=\begin{cases} 1 & \text{if }d\text{ is square-free},\\ 0 & \text{otherwise}. \end{cases} \end{align} $$
Note that this identity holds without the condition
![]() $(\alpha ,2N)=1$
, but this can be added, as by construction
$(\alpha ,2N)=1$
, but this can be added, as by construction
![]() $(d,2N)=1$
for
$(d,2N)=1$
for
![]() $d\in \mathcal D_{N,\eta }$
. Inserting this into the expression (37) that the d-sum is given by
$d\in \mathcal D_{N,\eta }$
. Inserting this into the expression (37) that the d-sum is given by
 $$ \begin{align*} \sum_{\substack{\alpha=1\\ \left(\alpha,2Nu\right)=1}}^\infty\mu(\alpha)\left(\frac{\alpha^2}{mu}\right)\sum_{r\equiv\eta\overline{\alpha^2}\pmod{4N}}\left(\frac r{mu}\right)W_{g,\eta}\left(\frac m{r\alpha^2}\right)\Phi\left(\frac{r\alpha^2}X\right). \end{align*} $$
$$ \begin{align*} \sum_{\substack{\alpha=1\\ \left(\alpha,2Nu\right)=1}}^\infty\mu(\alpha)\left(\frac{\alpha^2}{mu}\right)\sum_{r\equiv\eta\overline{\alpha^2}\pmod{4N}}\left(\frac r{mu}\right)W_{g,\eta}\left(\frac m{r\alpha^2}\right)\Phi\left(\frac{r\alpha^2}X\right). \end{align*} $$
We will evaluate the r-sum by applying a version of the Poisson summation formula [Reference Resnikoff and Saldana50, Lemma 7]. The terms where
![]() $mu$
is a square will contribute the main term in the zero-frequency term on the dual side, and the rest will give the error term. Using standard arguments [Reference Lester and Radziwiłł39], the contribution of the latter terms can be bounded by
$mu$
is a square will contribute the main term in the zero-frequency term on the dual side, and the rest will give the error term. Using standard arguments [Reference Lester and Radziwiłł39], the contribution of the latter terms can be bounded by
![]() $\ll _{k,N, \Phi , \varepsilon } X^{7/8+\varepsilon }u^{3/8+\varepsilon }$
.
$\ll _{k,N, \Phi , \varepsilon } X^{7/8+\varepsilon }u^{3/8+\varepsilon }$
.
Using equation (36), the zero-frequency contribution is given by
 $$ \begin{align} & \frac{X}{2N}\cdot\frac1{2\pi i}\int_{(c)}\left(\int_0^\infty\Phi(\xi)\xi^s\mathrm d \xi\right)L_{g,\eta}\left(s+\tfrac12\right)\frac{\Gamma(s+k)}{\Gamma(k)}\left(\frac{\sqrt \ell X}{2\pi}\right)^s \nonumber\\ &\quad \times \sum_{\substack{\alpha=1\\ \left(\alpha,2Nu\right)=1}}^\infty\frac{\mu(\alpha)}{\alpha^2}\sum_{\substack{m=1\\ \left(m,2N\alpha\right)=1\\ mu \text{ is a square}}}^\infty\frac{\lambda_g(m)}{m^{s+1/2}}\frac{\varphi(mu)}{mu}\frac{\mathrm d s}s. \end{align} $$
$$ \begin{align} & \frac{X}{2N}\cdot\frac1{2\pi i}\int_{(c)}\left(\int_0^\infty\Phi(\xi)\xi^s\mathrm d \xi\right)L_{g,\eta}\left(s+\tfrac12\right)\frac{\Gamma(s+k)}{\Gamma(k)}\left(\frac{\sqrt \ell X}{2\pi}\right)^s \nonumber\\ &\quad \times \sum_{\substack{\alpha=1\\ \left(\alpha,2Nu\right)=1}}^\infty\frac{\mu(\alpha)}{\alpha^2}\sum_{\substack{m=1\\ \left(m,2N\alpha\right)=1\\ mu \text{ is a square}}}^\infty\frac{\lambda_g(m)}{m^{s+1/2}}\frac{\varphi(mu)}{mu}\frac{\mathrm d s}s. \end{align} $$
A simple computation shows that for
![]() $(m,2N)=1$
,
$(m,2N)=1$
,
 $$ \begin{align*} \sum_{\substack{\alpha=1\\ \left(\alpha,2Num\right)=1}}^\infty\frac{\mu(\alpha)}{\alpha^2}\cdot\frac{\varphi(mu)}{mu}=\prod_{p\nmid 2N}\left(1-\frac1{p^2}\right)\prod_{p\mid um}\left(1+\frac1p\right)^{-1}, \end{align*} $$
$$ \begin{align*} \sum_{\substack{\alpha=1\\ \left(\alpha,2Num\right)=1}}^\infty\frac{\mu(\alpha)}{\alpha^2}\cdot\frac{\varphi(mu)}{mu}=\prod_{p\nmid 2N}\left(1-\frac1{p^2}\right)\prod_{p\mid um}\left(1+\frac1p\right)^{-1}, \end{align*} $$
leading to
 $$ \begin{align} & \sum_{\substack{\alpha=1\\ \left(\alpha,2Nu\right)=1}}^\infty\frac{\mu(\alpha)}{\alpha^2}\sum_{\substack{m=1\\ \left(m,2N\alpha\right)=1\\ mu \text{ is a square}}}^\infty\frac{\lambda_g(m)}{m^{s+1/2}}\cdot\frac{\varphi(mu)}{mu} \nonumber \\ &\quad =\prod_{p\nmid 2N}\left(1-\frac1{p^2}\right)\sum_{\substack{m=1\\ \left(m,2N\right)=1\\ mu \text{ is a square}}}^\infty\frac{\lambda_g(m)}{m^{s+1/2}}\prod_{p|um}\left(1+\frac1p\right)^{-1}. \end{align} $$
$$ \begin{align} & \sum_{\substack{\alpha=1\\ \left(\alpha,2Nu\right)=1}}^\infty\frac{\mu(\alpha)}{\alpha^2}\sum_{\substack{m=1\\ \left(m,2N\alpha\right)=1\\ mu \text{ is a square}}}^\infty\frac{\lambda_g(m)}{m^{s+1/2}}\cdot\frac{\varphi(mu)}{mu} \nonumber \\ &\quad =\prod_{p\nmid 2N}\left(1-\frac1{p^2}\right)\sum_{\substack{m=1\\ \left(m,2N\right)=1\\ mu \text{ is a square}}}^\infty\frac{\lambda_g(m)}{m^{s+1/2}}\prod_{p|um}\left(1+\frac1p\right)^{-1}. \end{align} $$
For
![]() $mu\text { a square}$
and
$mu\text { a square}$
and
![]() $u=u_1u_2^2$
with
$u=u_1u_2^2$
with
![]() $u_1$
square-free, it follows that
$u_1$
square-free, it follows that
![]() $m=u_1\ell ^2$
for some
$m=u_1\ell ^2$
for some
![]() $\ell \in \mathbb Z$
. Hence the right-hand side of the previous display is
$\ell \in \mathbb Z$
. Hence the right-hand side of the previous display is
 $$ \begin{align*} &\prod_{p\nmid 2N} \left(1-\frac1{p^2}\right)\sum_{\substack{\ell=1\\ \left(\ell,2N\right)=1}}^\infty\frac{\lambda_g\left(u_1\ell^2\right)}{u_1^{s+1/2}\ell^{2s+1}}\prod_{p\mid u\ell}\left(1+\frac1p\right)^{-1}\\ &=\frac1{u_1^{s+1/2}}\prod_{p\nmid 2N} \!\left( \! 1-\frac1{p^2} \!\right)\!\prod_{p\nmid 2Nu}\!\left(\! 1+\sum_{k=1}^\infty\frac{\lambda_g \!\left(\! p^{2k} \!\right)}{p^{k(2s+1)}}\!\left(\!1+\frac1p\right)^{-1}\!\right) \\ &\qquad \times \prod_{p\mid u}\!\left(\sum_{k=0}^\infty\frac{\lambda_g\left(p^{2k+\text{ord}_p\left(u_1\right)}\right)}{p^{k(2s+1)}}\!\right)\!\left(\!1+\frac1p \!\right)^{-1}\\ &=\frac1{u_1^{s+1/2}}L\left(2s+1,\text{Sym}^2g\right)\prod_{p\mid 2N}L_p\left(2s+1,\text{Sym}^2h\right)^{-1}\prod_{p\mid u}\left(1-\frac{1}p\right)\left(\sum_{k=0}^\infty\frac{\lambda_g\left(p^{2k+\text{ord}_p\left(u_1\right)}\right)}{p^{k(2s+1)}}\right)\\ &\quad\cdot L_p\left(2s+1,\text{Sym}^2g\right)^{-1}\prod_{p\nmid 2Nu}\!\left(\! 1-\frac1{p^2}\!\right)\!\left(\! 1+\sum_{k=1}^\infty\frac{\lambda_g(p^{2k})}{p^{k(2s+1)}}{\!\left(\! 1+\frac1p \!\right)\!}^{-1} \!\right)\! L_p\left(2s+1,\text{Sym}^2g\right)^{-1}. \end{align*} $$
$$ \begin{align*} &\prod_{p\nmid 2N} \left(1-\frac1{p^2}\right)\sum_{\substack{\ell=1\\ \left(\ell,2N\right)=1}}^\infty\frac{\lambda_g\left(u_1\ell^2\right)}{u_1^{s+1/2}\ell^{2s+1}}\prod_{p\mid u\ell}\left(1+\frac1p\right)^{-1}\\ &=\frac1{u_1^{s+1/2}}\prod_{p\nmid 2N} \!\left( \! 1-\frac1{p^2} \!\right)\!\prod_{p\nmid 2Nu}\!\left(\! 1+\sum_{k=1}^\infty\frac{\lambda_g \!\left(\! p^{2k} \!\right)}{p^{k(2s+1)}}\!\left(\!1+\frac1p\right)^{-1}\!\right) \\ &\qquad \times \prod_{p\mid u}\!\left(\sum_{k=0}^\infty\frac{\lambda_g\left(p^{2k+\text{ord}_p\left(u_1\right)}\right)}{p^{k(2s+1)}}\!\right)\!\left(\!1+\frac1p \!\right)^{-1}\\ &=\frac1{u_1^{s+1/2}}L\left(2s+1,\text{Sym}^2g\right)\prod_{p\mid 2N}L_p\left(2s+1,\text{Sym}^2h\right)^{-1}\prod_{p\mid u}\left(1-\frac{1}p\right)\left(\sum_{k=0}^\infty\frac{\lambda_g\left(p^{2k+\text{ord}_p\left(u_1\right)}\right)}{p^{k(2s+1)}}\right)\\ &\quad\cdot L_p\left(2s+1,\text{Sym}^2g\right)^{-1}\prod_{p\nmid 2Nu}\!\left(\! 1-\frac1{p^2}\!\right)\!\left(\! 1+\sum_{k=1}^\infty\frac{\lambda_g(p^{2k})}{p^{k(2s+1)}}{\!\left(\! 1+\frac1p \!\right)\!}^{-1} \!\right)\! L_p\left(2s+1,\text{Sym}^2g\right)^{-1}. \end{align*} $$
From this it is easy to see, by using the Euler product expression of the symmetric square L-function, that for
![]() $p\nmid 2Nu$
the corresponding Euler factor is
$p\nmid 2Nu$
the corresponding Euler factor is
 $$ \begin{align*} =\left(1-\frac1p\right)\left(1-\frac1{p^{2s+1}}\right)\left(\frac1p\left(1-\frac{\alpha_p^2}{p^{2s+1}}\right)\left(1-\frac{\beta_p^2}{p^{2s+1}}\right)+1+\frac1{p^{2s+1}}\right), \end{align*} $$
$$ \begin{align*} =\left(1-\frac1p\right)\left(1-\frac1{p^{2s+1}}\right)\left(\frac1p\left(1-\frac{\alpha_p^2}{p^{2s+1}}\right)\left(1-\frac{\beta_p^2}{p^{2s+1}}\right)+1+\frac1{p^{2s+1}}\right), \end{align*} $$
where
![]() $\left \{\alpha _p,\beta _p\right \}$
are the Satake parameters of the cusp form g at p.
$\left \{\alpha _p,\beta _p\right \}$
are the Satake parameters of the cusp form g at p.
Similarly, for
![]() $p\mid u, p\nmid u_1$
, the corresponding Euler factor is
$p\mid u, p\nmid u_1$
, the corresponding Euler factor is
 $\left (1-\frac {1}{p}\right )\left (1-\frac 1{p^{4s+2}}\right )$
. For
$\left (1-\frac {1}{p}\right )\left (1-\frac 1{p^{4s+2}}\right )$
. For
![]() $p\mid u_1$
, the corresponding Euler factor is
$p\mid u_1$
, the corresponding Euler factor is
 $\left (1-\frac {1}{p}\right )\left (1-\frac 1{p^{2s+1}}\right )\lambda _g(p)$
by using the relations
$\left (1-\frac {1}{p}\right )\left (1-\frac 1{p^{2s+1}}\right )\lambda _g(p)$
by using the relations
 $\lambda _g\left (p^j\right )=\left (\alpha _p^{j+1}-\beta _p^{j+1}\right )/\left (\alpha _p-\beta _p\right )$
for
$\lambda _g\left (p^j\right )=\left (\alpha _p^{j+1}-\beta _p^{j+1}\right )/\left (\alpha _p-\beta _p\right )$
for
![]() $j\geq 0$
and
$j\geq 0$
and
![]() $\alpha _p\beta _p=1$
. And finally, for
$\alpha _p\beta _p=1$
. And finally, for
![]() $p\mid 2N$
the corresponding Euler factor is clearly
$p\mid 2N$
the corresponding Euler factor is clearly
 $L_p\left (2s+1,\text {Sym}^2g\right )^{-1}$
.
$L_p\left (2s+1,\text {Sym}^2g\right )^{-1}$
.
To summarize, the right-hand side of equation (40) equals
 $$ \begin{align*} \frac{\lambda_g(u_1)}{u_1^{s+1/2}}L\left(2s+1,\text{Sym}^2g\right)\mathcal G(2s+1;u), \end{align*} $$
$$ \begin{align*} \frac{\lambda_g(u_1)}{u_1^{s+1/2}}L\left(2s+1,\text{Sym}^2g\right)\mathcal G(2s+1;u), \end{align*} $$
where
 $\mathcal G(2s+1;u)=\prod _p \mathcal G_p(2s+1;u)$
is the Euler product locally given by
$\mathcal G(2s+1;u)=\prod _p \mathcal G_p(2s+1;u)$
is the Euler product locally given by
 $$ \begin{align} &\mathcal G_p(2s+1;u)\nonumber\\&\quad =\begin{cases} L_p\left(2s+1,\text{Sym}^2 g\right)^{-1}&\text{if }p\mid 2N,\\ \left(1-\frac1{p}\right)\left(1-\frac1{p^{2s+1}}\right)&\text{if }p\mid u_1,\\ \left(1-\frac1{p}\right)\left(1-\frac1{p^{4s+2}}\right)&\text{if }p\mid u_2,\ p\nmid u_1,\\ \left(1-\frac1p\right)\left(1-\frac1{p^{2s+1}}\right)\left(1+\frac1p\left(1-\frac{\alpha_p^2}{p^{2s+1}}\right)\left(1-\frac{\beta_p^2}{p^{2s+1}}\right)+\frac1{p^{2s+1}}\right)&\text{if }p\nmid 2Nu. \end{cases} \end{align} $$
$$ \begin{align} &\mathcal G_p(2s+1;u)\nonumber\\&\quad =\begin{cases} L_p\left(2s+1,\text{Sym}^2 g\right)^{-1}&\text{if }p\mid 2N,\\ \left(1-\frac1{p}\right)\left(1-\frac1{p^{2s+1}}\right)&\text{if }p\mid u_1,\\ \left(1-\frac1{p}\right)\left(1-\frac1{p^{4s+2}}\right)&\text{if }p\mid u_2,\ p\nmid u_1,\\ \left(1-\frac1p\right)\left(1-\frac1{p^{2s+1}}\right)\left(1+\frac1p\left(1-\frac{\alpha_p^2}{p^{2s+1}}\right)\left(1-\frac{\beta_p^2}{p^{2s+1}}\right)+\frac1{p^{2s+1}}\right)&\text{if }p\nmid 2Nu. \end{cases} \end{align} $$
By estimating trivially, it follows that
![]() $\mathcal G(2s+1;u)$
extends analytically to the domain
$\mathcal G(2s+1;u)$
extends analytically to the domain
![]() $\mathrm {Re}(s)>-1/4$
and is bounded there by
$\mathrm {Re}(s)>-1/4$
and is bounded there by
 $$ \begin{align*} \ll\prod_{p\nmid 2Nu}\left(1+\frac{O(1)}{\sqrt p}\right)\ll_{N,\varepsilon} u^\varepsilon. \end{align*} $$
$$ \begin{align*} \ll\prod_{p\nmid 2Nu}\left(1+\frac{O(1)}{\sqrt p}\right)\ll_{N,\varepsilon} u^\varepsilon. \end{align*} $$
Consequently, the s-integrand in the expression (39) extends to an analytic function the domain
![]() $\mathrm {Re}(s)>-1/4$
(apart from a simple pole at
$\mathrm {Re}(s)>-1/4$
(apart from a simple pole at
![]() $s=0$
). Thus moving the line of integration in formula (39) to the line
$s=0$
). Thus moving the line of integration in formula (39) to the line
![]() $\mathrm {Re}(s)=-1/4+\varepsilon $
shows that the expression equals
$\mathrm {Re}(s)=-1/4+\varepsilon $
shows that the expression equals
 $$ \begin{align*} \frac{X\lambda_g(u_1)}{2Nu_1^{1/2}}\left(\int_0^\infty\Phi(\xi)\mathrm d \xi\right)L_{g,\eta}\left(\frac12\right)L\left(1,\text{Sym}^2g\right)\mathcal G(1;u)+O_{k,N, \Phi, \varepsilon}\left(X^{3/4+\varepsilon}\right), \end{align*} $$
$$ \begin{align*} \frac{X\lambda_g(u_1)}{2Nu_1^{1/2}}\left(\int_0^\infty\Phi(\xi)\mathrm d \xi\right)L_{g,\eta}\left(\frac12\right)L\left(1,\text{Sym}^2g\right)\mathcal G(1;u)+O_{k,N, \Phi, \varepsilon}\left(X^{3/4+\varepsilon}\right), \end{align*} $$
where the main term comes from the residue at
![]() $s=0$
and the error term from the contour shift. It follows immediately from the definition of
$s=0$
and the error term from the contour shift. It follows immediately from the definition of
![]() $\mathcal G(s;u)$
that
$\mathcal G(s;u)$
that
![]() $\mathcal G(1;\cdot )$
is multiplicative and that
$\mathcal G(1;\cdot )$
is multiplicative and that
 $\mathcal G\left (1;p^k\right )=1+O(1/p)$
at prime powers. This concludes the sketch of the proof of Proposition 4.3.
$\mathcal G\left (1;p^k\right )=1+O(1/p)$
at prime powers. This concludes the sketch of the proof of Proposition 4.3.
4.4. Proofs of the estimates
We are now ready to prove the estimates (31) and (32). As the arguments are similar to [Reference Gun and Sengupta21], we will be brief. Let us denote
 $$ \begin{align*} A_{g,\eta}(\Phi)=\frac1{2N}\left(\int_0^\infty\Phi(\xi)\mathrm d \xi\right)L_{g,\eta}\left(\frac12\right)L\left(1,\text{Sym}^2g\right) \end{align*} $$
$$ \begin{align*} A_{g,\eta}(\Phi)=\frac1{2N}\left(\int_0^\infty\Phi(\xi)\mathrm d \xi\right)L_{g,\eta}\left(\frac12\right)L\left(1,\text{Sym}^2g\right) \end{align*} $$
and
 $$ \begin{align*} B_g(u)=\frac{\lambda_g\left(u_1\right)}{u_1^{1/2}}\mathcal G(1;u) \end{align*} $$
$$ \begin{align*} B_g(u)=\frac{\lambda_g\left(u_1\right)}{u_1^{1/2}}\mathcal G(1;u) \end{align*} $$
for
![]() $u=u_1u_2^2$
with
$u=u_1u_2^2$
with
![]() $u_1$
square-free.
$u_1$
square-free.
Let
![]() $\Phi $
be a compactly supported smooth weight function. Our aim is now to evaluate
$\Phi $
be a compactly supported smooth weight function. Our aim is now to evaluate
 $$ \begin{align} \sum_{d\in\mathcal D_{N,\eta}}L\left(\tfrac12,g\otimes\chi_d\right)\lvert R(d)\rvert^2\Phi\left(\frac{\lvert d\rvert}X\right) \end{align} $$
$$ \begin{align} \sum_{d\in\mathcal D_{N,\eta}}L\left(\tfrac12,g\otimes\chi_d\right)\lvert R(d)\rvert^2\Phi\left(\frac{\lvert d\rvert}X\right) \end{align} $$
for
![]() $g=g_f\in S_{2k}^{\mathrm {new}}(\ell )$
, where
$g=g_f\in S_{2k}^{\mathrm {new}}(\ell )$
, where
 $f\in {\mathcal B}_{k+\frac 12,4\ell }^{\mathrm {new}}$
with
$f\in {\mathcal B}_{k+\frac 12,4\ell }^{\mathrm {new}}$
with
![]() $\ell \mid N$
, by choosing
$\ell \mid N$
, by choosing
![]() $\Phi $
appropriately for given f.
$\Phi $
appropriately for given f.
By opening the definition of
![]() $R(d)$
and using Proposition 4.3, the sum (42) equals
$R(d)$
and using Proposition 4.3, the sum (42) equals
 $$ \begin{align*} \sum_{d\in\mathcal D_{N,\eta}} & L\left(\tfrac12,g\otimes\chi_d\right)\Phi\left(\frac{\lvert d\rvert}X\right)\sum_{n_1,n_2\leq M}r(n_1)r(n_2)\lambda_0(n_1)\lambda_0(n_2)\chi_d(n_1n_2)\\ &=X\cdot A_{g,\eta}(\Phi)\sum_{n_1,n_2\leq M}r(n_1)r(n_2)\lambda_0(n_1)\lambda_0(n_2)B_g\left(n_1n_2\right)\\ &\quad +O_{k,N,\Phi,\varepsilon}\left(X^{7/8+\varepsilon}\sum_{n_1,n_2\leq M}r(n_1)r(n_2)\lvert\lambda_0(n_1)\lambda_0(n_2)\rvert(n_1n_2)^{3/8+\varepsilon}\right) \end{align*} $$
$$ \begin{align*} \sum_{d\in\mathcal D_{N,\eta}} & L\left(\tfrac12,g\otimes\chi_d\right)\Phi\left(\frac{\lvert d\rvert}X\right)\sum_{n_1,n_2\leq M}r(n_1)r(n_2)\lambda_0(n_1)\lambda_0(n_2)\chi_d(n_1n_2)\\ &=X\cdot A_{g,\eta}(\Phi)\sum_{n_1,n_2\leq M}r(n_1)r(n_2)\lambda_0(n_1)\lambda_0(n_2)B_g\left(n_1n_2\right)\\ &\quad +O_{k,N,\Phi,\varepsilon}\left(X^{7/8+\varepsilon}\sum_{n_1,n_2\leq M}r(n_1)r(n_2)\lvert\lambda_0(n_1)\lambda_0(n_2)\rvert(n_1n_2)^{3/8+\varepsilon}\right) \end{align*} $$
as
![]() $r(n)$
vanishes, unless
$r(n)$
vanishes, unless
![]() $(n,N)=1$
. Using Deligne’s bound, we obtain as in [Reference Gun and Sengupta21, §6] that the error term is
$(n,N)=1$
. Using Deligne’s bound, we obtain as in [Reference Gun and Sengupta21, §6] that the error term is
![]() $\ll _{k,N,\Phi } X^{99/100}$
.
$\ll _{k,N,\Phi } X^{99/100}$
.
By making use of the fact that
 $$ \begin{align*} n_1n_2=\frac{n_1n_2}{(n_1,n_2)^2}\cdot(n_1,n_2)^2, \end{align*} $$
$$ \begin{align*} n_1n_2=\frac{n_1n_2}{(n_1,n_2)^2}\cdot(n_1,n_2)^2, \end{align*} $$
with the first factor on the right-hand side square-free in our case, as the function
![]() $r(n)$
is supported only on square-free integers, the main term can be written as
$r(n)$
is supported only on square-free integers, the main term can be written as
 $$ \begin{align*} X\cdot A_{g,\eta}(\Phi)\sum_{n_1,n_2\leq M}r(n_1)r(n_2)\lambda_0(n_1)\lambda_0(n_2)\frac{\lambda_g\left(\frac{n_1n_2}{(n_1,n_2)^2}\right)}{\left(\frac{n_1n_2}{(n_1,n_2)^2}\right)^{1/2}}\cdot\mathcal G(1;n_1n_2). \end{align*} $$
$$ \begin{align*} X\cdot A_{g,\eta}(\Phi)\sum_{n_1,n_2\leq M}r(n_1)r(n_2)\lambda_0(n_1)\lambda_0(n_2)\frac{\lambda_g\left(\frac{n_1n_2}{(n_1,n_2)^2}\right)}{\left(\frac{n_1n_2}{(n_1,n_2)^2}\right)^{1/2}}\cdot\mathcal G(1;n_1n_2). \end{align*} $$
Our aim is to use multiplicativity, and so we need to extend the sum over all integers. To do so we must show that the terms with max(
![]() $n_1,n_2)>M$
can be added with a tolerable error. Using Rankin’s trick, these terms contribute
$n_1,n_2)>M$
can be added with a tolerable error. Using Rankin’s trick, these terms contribute
 $$ \begin{align*} &\ll_{k,N} X\sum_{\max\left(n_1,n_2\right)>M}r(n_1)r(n_2)\lvert\lambda_0(n_1)\lambda_0(n_2)\rvert\cdot\lvert\mathcal G(1;n_1n_2)\rvert\cdot\left\lvert\frac{\lambda_g\left(\frac{n_1n_2}{(n_1,n_2)^2}\right)}{\left(\frac{n_1n_2}{(n_1,n_2)^2}\right)^{1/2}}\right\rvert\\ &\ll_{k,N} X\sum_{n_1,n_2=1}^\infty r(n_1)r(n_2)\lvert\lambda_0(n_1)\lambda_0(n_2)\rvert\cdot\lvert\mathcal G(1;n_1n_2)\rvert\cdot\left\lvert\frac{\lambda_g\left(\frac{n_1n_2}{(n_1,n_2)^2}\right)}{\left(\frac{n_1n_2}{(n_1,n_2)^2}\right)^{1/2}}\right\rvert\left(\frac{n_1n_2}M\right)^\alpha \end{align*} $$
$$ \begin{align*} &\ll_{k,N} X\sum_{\max\left(n_1,n_2\right)>M}r(n_1)r(n_2)\lvert\lambda_0(n_1)\lambda_0(n_2)\rvert\cdot\lvert\mathcal G(1;n_1n_2)\rvert\cdot\left\lvert\frac{\lambda_g\left(\frac{n_1n_2}{(n_1,n_2)^2}\right)}{\left(\frac{n_1n_2}{(n_1,n_2)^2}\right)^{1/2}}\right\rvert\\ &\ll_{k,N} X\sum_{n_1,n_2=1}^\infty r(n_1)r(n_2)\lvert\lambda_0(n_1)\lambda_0(n_2)\rvert\cdot\lvert\mathcal G(1;n_1n_2)\rvert\cdot\left\lvert\frac{\lambda_g\left(\frac{n_1n_2}{(n_1,n_2)^2}\right)}{\left(\frac{n_1n_2}{(n_1,n_2)^2}\right)^{1/2}}\right\rvert\left(\frac{n_1n_2}M\right)^\alpha \end{align*} $$
for any
![]() $\alpha>0$
, which is chosen optimally later.
$\alpha>0$
, which is chosen optimally later.
Write
![]() $n=n_1n_2$
to express the double sum as a single sum over n, and note that by the fact that
$n=n_1n_2$
to express the double sum as a single sum over n, and note that by the fact that
![]() $r(\cdot )$
is supported only on square-free integers coprime to N, the only integers n which contribute to the sum over n satisfy
$r(\cdot )$
is supported only on square-free integers coprime to N, the only integers n which contribute to the sum over n satisfy
![]() $p^3 \nmid n$
and
$p^3 \nmid n$
and
![]() $(n,N)=1$
. Hence, by the multiplicativity of
$(n,N)=1$
. Hence, by the multiplicativity of
![]() $r(\cdot )$
we can express the sum over n as an Euler product, and the expression on the right-hand side of the previous display equals
$r(\cdot )$
we can express the sum over n as an Euler product, and the expression on the right-hand side of the previous display equals
 $$ \begin{align*} &= XM^{-\alpha}\prod_{L^2\leq p\leq L^4}\left(1+2r(p)p^{\alpha-1/2}\lvert\mathcal G(1;p)\rvert\cdot\frac{\left\lvert\lambda_0(p)\lambda_g(p)\right\rvert}{\sqrt p}+r(p)^2p^{2\alpha}\left\lvert\mathcal G\left(1;p^2\right)\right\rvert\cdot\lvert\lambda_0(p)\rvert^2\right)\\ &\ll XM^{-\alpha}\exp\left(\sum_{L^2\leq p\leq L^4} \left(\frac{8Lp^{\alpha-1}}{\log p}+\frac{4L^2p^{2\alpha-1}}{(\log p)^2}\right) \left( 1+O\left( \frac1p\right)\right)\right), \end{align*} $$
$$ \begin{align*} &= XM^{-\alpha}\prod_{L^2\leq p\leq L^4}\left(1+2r(p)p^{\alpha-1/2}\lvert\mathcal G(1;p)\rvert\cdot\frac{\left\lvert\lambda_0(p)\lambda_g(p)\right\rvert}{\sqrt p}+r(p)^2p^{2\alpha}\left\lvert\mathcal G\left(1;p^2\right)\right\rvert\cdot\lvert\lambda_0(p)\rvert^2\right)\\ &\ll XM^{-\alpha}\exp\left(\sum_{L^2\leq p\leq L^4} \left(\frac{8Lp^{\alpha-1}}{\log p}+\frac{4L^2p^{2\alpha-1}}{(\log p)^2}\right) \left( 1+O\left( \frac1p\right)\right)\right), \end{align*} $$
where the last estimate follows from Deligne’s bound
![]() $\left \lvert \lambda _g(p)\right \rvert \leq 2$
, the fact that
$\left \lvert \lambda _g(p)\right \rvert \leq 2$
, the fact that
 $\mathcal G\left (1;p^k\right )=1+O(1/p)$
, and the definition of
$\mathcal G\left (1;p^k\right )=1+O(1/p)$
, and the definition of
![]() $r(n)$
.
$r(n)$
.
Let us now choose
![]() $\alpha =1/(8\log L)$
. Then by the prime number theorem and partial summation, the previous is
$\alpha =1/(8\log L)$
. Then by the prime number theorem and partial summation, the previous is
 $$ \begin{align*} \ll X\cdot\exp\left(-\frac{\log M}{8\log L}+\frac{8L}{\log L}+\frac{4L^2}{(\log L)^2}\right)\ll X \end{align*} $$
$$ \begin{align*} \ll X\cdot\exp\left(-\frac{\log M}{8\log L}+\frac{8L}{\log L}+\frac{4L^2}{(\log L)^2}\right)\ll X \end{align*} $$
by the choices
 $L=\frac 18\sqrt {\log M\log \log M}$
and
$L=\frac 18\sqrt {\log M\log \log M}$
and
![]() $M=X^{1/24}$
. From the foregoing arguments we deduce that
$M=X^{1/24}$
. From the foregoing arguments we deduce that
 $$ \begin{align} &\sum_{d\in\mathcal D_{N,\eta}} L\left(\frac12,g\otimes\chi_d\right)\lvert R(d)\rvert^2\Phi\left(\frac{\lvert d\rvert}X\right)\\ &\quad = A_{g,\eta}(\Phi)\cdot X\cdot\prod_{L^2\leq p\leq L^4}\!\left(\! 1+2r(p)\mathcal G(1;p)\cdot\frac{\lambda_0(p)\lambda_g(p)}{\sqrt p}+r(p)^2\mathcal G(1;p^2)\cdot \lambda_0(p)^2 \!\right) \nonumber \\ &\qquad +O_{k,N,\Phi}(X) \nonumber \\ &\quad =A_{g,\eta}(\Phi)\cdot X\cdot\mathcal R\cdot\exp \!\left(\! 2\sum_{L^2\leq p\leq L^4}\frac{r(p)\lambda_0(p)\lambda_g(p)}{\sqrt p}+O_{k,N,\Phi} \!\left(\frac L{(\log L)^3} \!\right)\!\right)\! + O_{k,N,\Phi}(X), \nonumber \end{align} $$
$$ \begin{align} &\sum_{d\in\mathcal D_{N,\eta}} L\left(\frac12,g\otimes\chi_d\right)\lvert R(d)\rvert^2\Phi\left(\frac{\lvert d\rvert}X\right)\\ &\quad = A_{g,\eta}(\Phi)\cdot X\cdot\prod_{L^2\leq p\leq L^4}\!\left(\! 1+2r(p)\mathcal G(1;p)\cdot\frac{\lambda_0(p)\lambda_g(p)}{\sqrt p}+r(p)^2\mathcal G(1;p^2)\cdot \lambda_0(p)^2 \!\right) \nonumber \\ &\qquad +O_{k,N,\Phi}(X) \nonumber \\ &\quad =A_{g,\eta}(\Phi)\cdot X\cdot\mathcal R\cdot\exp \!\left(\! 2\sum_{L^2\leq p\leq L^4}\frac{r(p)\lambda_0(p)\lambda_g(p)}{\sqrt p}+O_{k,N,\Phi} \!\left(\frac L{(\log L)^3} \!\right)\!\right)\! + O_{k,N,\Phi}(X), \nonumber \end{align} $$
where the last step follows exactly as in [Reference Gun and Sengupta21, §6].
We now apply this result with
![]() $g=g_f$
, where
$g=g_f$
, where
 $f\in {\mathcal B}_{k+\frac 12,4\ell }^{\mathrm {new}}$
with
$f\in {\mathcal B}_{k+\frac 12,4\ell }^{\mathrm {new}}$
with
![]() $\ell \mid N$
. For the estimate (31) we choose
$\ell \mid N$
. For the estimate (31) we choose
![]() $\Phi $
to be supported on the interval
$\Phi $
to be supported on the interval
![]() $[1,2]$
such that
$[1,2]$
such that
![]() $\Phi (t)=1$
for
$\Phi (t)=1$
for
![]() $t\in [11/10,19/10]$
and satisfying
$t\in [11/10,19/10]$
and satisfying
![]() $0\leq \Phi (t)\leq 1$
. For the estimate (32) we choose
$0\leq \Phi (t)\leq 1$
. For the estimate (32) we choose
![]() $\Phi $
to be supported in
$\Phi $
to be supported in
![]() $[1/2, 5/2]$
with
$[1/2, 5/2]$
with
![]() $\Phi (t)=1$
for
$\Phi (t)=1$
for
![]() $t\in [1,2]$
and again satisfying
$t\in [1,2]$
and again satisfying
![]() $0\leq \Phi (t)\leq 1$
. These choices lead to
$0\leq \Phi (t)\leq 1$
. These choices lead to
 $$ \begin{align*} & \sum_{d\in\mathcal D_{N,\eta}(X)} L\left(\frac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2\\ &\quad \geq\frac{4X\mathcal R}{5N}\cdot L_{g_0,\eta}\left(\frac12\right)L\left(1,\text{Sym}^2g_0\right)\cdot\exp\left(2\sum_{L^2\leq p\leq L^4}\frac{r(p)\lambda_0(p)^2}{\sqrt p}+O\left(\frac L{(\log L)^3}\right)\right)\\ &\qquad +O_{k,N}(X) \end{align*} $$
$$ \begin{align*} & \sum_{d\in\mathcal D_{N,\eta}(X)} L\left(\frac12,g_0\otimes\chi_d\right)\lvert R(d)\rvert^2\\ &\quad \geq\frac{4X\mathcal R}{5N}\cdot L_{g_0,\eta}\left(\frac12\right)L\left(1,\text{Sym}^2g_0\right)\cdot\exp\left(2\sum_{L^2\leq p\leq L^4}\frac{r(p)\lambda_0(p)^2}{\sqrt p}+O\left(\frac L{(\log L)^3}\right)\right)\\ &\qquad +O_{k,N}(X) \end{align*} $$
for
![]() $f=f_0$
and
$f=f_0$
and
 $$ \begin{align*} &\sum_{d\in\mathcal D_{N,\eta}(X)} L\left(\frac12,g_f\otimes\chi_d\right)\lvert R(d)\rvert^2\\ &\quad \leq\frac{X\mathcal R}N\cdot L_{g_f,\eta}\left(\frac12\right)L\left(1,\text{Sym}^2g_f\right)\exp\left(2\sum_{L^2\leq p\leq L^4}\frac{r(p)\lambda_0(p)\lambda_{g_f}(p)}{\sqrt p}+O\left(\frac L{(\log L)^3}\right)\right)\\ &\qquad +O_{k,N}(X) \end{align*} $$
$$ \begin{align*} &\sum_{d\in\mathcal D_{N,\eta}(X)} L\left(\frac12,g_f\otimes\chi_d\right)\lvert R(d)\rvert^2\\ &\quad \leq\frac{X\mathcal R}N\cdot L_{g_f,\eta}\left(\frac12\right)L\left(1,\text{Sym}^2g_f\right)\exp\left(2\sum_{L^2\leq p\leq L^4}\frac{r(p)\lambda_0(p)\lambda_{g_f}(p)}{\sqrt p}+O\left(\frac L{(\log L)^3}\right)\right)\\ &\qquad +O_{k,N}(X) \end{align*} $$
for
![]() $f\neq f_0$
.
$f\neq f_0$
.
To obtain the estimates (31) and (32) we use partial summation and the following estimate, which is a consequence of the Rankin–Selberg theory [Reference Wu and Ye69, Theorem 3]:
Lemma 4.4. With the notation as given, we have
 $$ \begin{align*} \sum_{p\leq x}\lambda_0(p)\lambda_{g_f}(p)\log p=x\cdot 1_{f=f_0}+o(x). \end{align*} $$
$$ \begin{align*} \sum_{p\leq x}\lambda_0(p)\lambda_{g_f}(p)\log p=x\cdot 1_{f=f_0}+o(x). \end{align*} $$
5. Siegel cusp forms of degree
 $2$
$2$
In this section we first review various properties of Siegel cusp forms of degree
![]() $2$
and then go on to prove our main results stated in the introduction.
$2$
and then go on to prove our main results stated in the introduction.
5.1. Preliminaries
Denote by J the
![]() $4 \times 4$
matrix given by
$4 \times 4$
matrix given by
 $ J = \left (\begin {smallmatrix} 0 & I_2\\ -I_2 & 0\\ \end {smallmatrix}\right )$
, where
$ J = \left (\begin {smallmatrix} 0 & I_2\\ -I_2 & 0\\ \end {smallmatrix}\right )$
, where
![]() $I_2$
is the identity matrix of size
$I_2$
is the identity matrix of size
![]() $2$
. Define the algebraic groups
$2$
. Define the algebraic groups
![]() ${\mathrm{GSp}}_4$
and
${\mathrm{GSp}}_4$
and
![]() $\mathrm {Sp}_4$
over
$\mathrm {Sp}_4$
over
![]() ${\mathbb Z}$
by
${\mathbb Z}$
by
 $$ \begin{gather*} {\textrm{GSp}}_4(R) = \left\{g \in {\textrm{GL}}_4(R) \mid {}^t\!{g}Jg = \mu_2(g)J, \ \mu_2(g)\in R^{\times}\right\}, \\ \mathrm{Sp}_4(R) = \{g \in {\textrm{GSp}}_4(R) \mid \mu_2(g)=1\}, \end{gather*} $$
$$ \begin{gather*} {\textrm{GSp}}_4(R) = \left\{g \in {\textrm{GL}}_4(R) \mid {}^t\!{g}Jg = \mu_2(g)J, \ \mu_2(g)\in R^{\times}\right\}, \\ \mathrm{Sp}_4(R) = \{g \in {\textrm{GSp}}_4(R) \mid \mu_2(g)=1\}, \end{gather*} $$
for any commutative ring R. The Siegel upper half-space
![]() $\mathbb H_2$
of degree
$\mathbb H_2$
of degree
![]() $2$
is defined by
$2$
is defined by
 $$ \begin{align*} \mathbb H_2 = \left\{ Z \in \mathrm{Mat}_{2\times 2}({\mathbb C}) \mid Z ={}^t\!{Z},\ \mathrm{Im}(Z) \text{ is positive definite}\right\}. \end{align*} $$
$$ \begin{align*} \mathbb H_2 = \left\{ Z \in \mathrm{Mat}_{2\times 2}({\mathbb C}) \mid Z ={}^t\!{Z},\ \mathrm{Im}(Z) \text{ is positive definite}\right\}. \end{align*} $$
Let k and N be positive integers. Let
 $\Gamma ^{(2)}_0(N) \subseteq \mathrm {Sp}_4({\mathbb Z})$
denote the Siegel congruence subgroup of level N – that is,
$\Gamma ^{(2)}_0(N) \subseteq \mathrm {Sp}_4({\mathbb Z})$
denote the Siegel congruence subgroup of level N – that is,
 $$ \begin{align} \Gamma^{(2)}_0(N) = \mathrm{Sp}_4({\mathbb Z}) \cap \left(\begin{smallmatrix}{\mathbb Z}& {\mathbb Z}&{\mathbb Z}&{\mathbb Z}\\{\mathbb Z}& {\mathbb Z}&{\mathbb Z}&{\mathbb Z}\\N{\mathbb Z}& N{\mathbb Z}&{\mathbb Z}&{\mathbb Z}\\N{\mathbb Z}&N {\mathbb Z}&{\mathbb Z}&{\mathbb Z}\\\end{smallmatrix}\right). \end{align} $$
$$ \begin{align} \Gamma^{(2)}_0(N) = \mathrm{Sp}_4({\mathbb Z}) \cap \left(\begin{smallmatrix}{\mathbb Z}& {\mathbb Z}&{\mathbb Z}&{\mathbb Z}\\{\mathbb Z}& {\mathbb Z}&{\mathbb Z}&{\mathbb Z}\\N{\mathbb Z}& N{\mathbb Z}&{\mathbb Z}&{\mathbb Z}\\N{\mathbb Z}&N {\mathbb Z}&{\mathbb Z}&{\mathbb Z}\\\end{smallmatrix}\right). \end{align} $$
We define
 $$ \begin{align*} g \langle Z\rangle = (AZ+B)(CZ+D)^{-1}\qquad\text{for } g=\left(\begin{smallmatrix} A&B\\ C&D \end{smallmatrix}\right) \in \mathrm{Sp}_4({\mathbb R}),\ Z\in \mathbb H_2. \end{align*} $$
$$ \begin{align*} g \langle Z\rangle = (AZ+B)(CZ+D)^{-1}\qquad\text{for } g=\left(\begin{smallmatrix} A&B\\ C&D \end{smallmatrix}\right) \in \mathrm{Sp}_4({\mathbb R}),\ Z\in \mathbb H_2. \end{align*} $$
We let
![]() $J(g,Z) = CZ + D$
. Let
$J(g,Z) = CZ + D$
. Let
 $S_k(\Gamma ^{(2)}_0(N))$
denote the space of Siegel cusp forms of weight k and level N; precisely, they consist of the holomorphic functions F on
$S_k(\Gamma ^{(2)}_0(N))$
denote the space of Siegel cusp forms of weight k and level N; precisely, they consist of the holomorphic functions F on
![]() $\mathbb H_2$
which satisfy the relation
$\mathbb H_2$
which satisfy the relation
for
 $\gamma \in \Gamma _0^{(2)}(N)$
,
$\gamma \in \Gamma _0^{(2)}(N)$
,
![]() $Z \in \mathbb H_2$
, and vanish at all the cusps. Any F in
$Z \in \mathbb H_2$
, and vanish at all the cusps. Any F in
 $S_k(\Gamma ^{(2)}_0(N))$
has a Fourier expansion
$S_k(\Gamma ^{(2)}_0(N))$
has a Fourier expansion
 $$ \begin{align}F(Z) =\sum_{S \in \Lambda_2} a(F, S) e^{2 \pi i \mathrm{Tr}(SZ)}, \end{align} $$
$$ \begin{align}F(Z) =\sum_{S \in \Lambda_2} a(F, S) e^{2 \pi i \mathrm{Tr}(SZ)}, \end{align} $$
with
![]() $\Lambda _2$
defined in equation (2). We have the relation
$\Lambda _2$
defined in equation (2). We have the relation
 $$ \begin{align} a(F, T) = \det(A)^ka\left(F, {}^t\!{A}TA\right) \end{align} $$
$$ \begin{align} a(F, T) = \det(A)^ka\left(F, {}^t\!{A}TA\right) \end{align} $$
for
![]() $A \in {\mathrm{GL}}_2({\mathbb Z})$
. In particular, the Fourier coefficient
$A \in {\mathrm{GL}}_2({\mathbb Z})$
. In particular, the Fourier coefficient
![]() $a(F, T)$
depends only on the
$a(F, T)$
depends only on the
![]() ${\mathrm{SL}}_2({\mathbb Z})$
-equivalence class of T. We say that a matrix
${\mathrm{SL}}_2({\mathbb Z})$
-equivalence class of T. We say that a matrix
![]() $S \in \Lambda _2$
is fundamental if
$S \in \Lambda _2$
is fundamental if
![]() ${\mathrm{disc}}(S)= -4 \det (S)$
is a fundamental discriminant. Given a fundamental discriminant
${\mathrm{disc}}(S)= -4 \det (S)$
is a fundamental discriminant. Given a fundamental discriminant
![]() $d<0$
and
$d<0$
and
![]() $K= {\mathbb Q}(\sqrt {d})$
, let
$K= {\mathbb Q}(\sqrt {d})$
, let
![]() $\operatorname {\mathrm {Cl}}_K$
denote the ideal class group of K. It is well known that the
$\operatorname {\mathrm {Cl}}_K$
denote the ideal class group of K. It is well known that the
![]() ${\mathrm{SL}}_2({\mathbb Z})$
-equivalence classes of matrices in
${\mathrm{SL}}_2({\mathbb Z})$
-equivalence classes of matrices in
![]() $\Lambda _2$
of discriminant d can be identified with
$\Lambda _2$
of discriminant d can be identified with
![]() $\operatorname {\mathrm {Cl}}_K$
; so the expression
$\operatorname {\mathrm {Cl}}_K$
; so the expression
![]() $\sum _{S \in \operatorname {\mathrm {Cl}}_K}a(F, S) \Lambda (S)$
makes sense for each
$\sum _{S \in \operatorname {\mathrm {Cl}}_K}a(F, S) \Lambda (S)$
makes sense for each
![]() $\Lambda \in \widehat {\operatorname {\mathrm {Cl}}_K}$
.
$\Lambda \in \widehat {\operatorname {\mathrm {Cl}}_K}$
.
5.2. Constructing half-integral-weight forms
Each F in
 $S_k(\Gamma ^{(2)}_0(N))$
has a Fourier–Jacobi expansion
$S_k(\Gamma ^{(2)}_0(N))$
has a Fourier–Jacobi expansion
 $F(Z) = \sum _{m> 0} \phi _m(\tau , z) e^{2 \pi i m \tau '}$
, where we write
$F(Z) = \sum _{m> 0} \phi _m(\tau , z) e^{2 \pi i m \tau '}$
, where we write
 $Z= \begin {pmatrix}\tau &z\\z&\tau ' \end {pmatrix}$
and for each
$Z= \begin {pmatrix}\tau &z\\z&\tau ' \end {pmatrix}$
and for each
![]() $m>0$
,
$m>0$
,
 $$ \begin{align} \phi_m(\tau, z) = \sum_{\substack{n,r \in {\mathbb Z} \\ 4nm> r^2}}a \left(F, {\left(\begin{array}{@{}cc@{}}n&r/2\\r/2&m\end{array}\right)}\right) e^{2\pi i (n \tau + r z)} \in J_{k,m}^{\text{cusp}}(N). \end{align} $$
$$ \begin{align} \phi_m(\tau, z) = \sum_{\substack{n,r \in {\mathbb Z} \\ 4nm> r^2}}a \left(F, {\left(\begin{array}{@{}cc@{}}n&r/2\\r/2&m\end{array}\right)}\right) e^{2\pi i (n \tau + r z)} \in J_{k,m}^{\text{cusp}}(N). \end{align} $$
Here
 $J_{k,m}^{\text {cusp}}(N)$
denotes the space of Jacobi cusp forms of weight k, level N, and index m.
$J_{k,m}^{\text {cusp}}(N)$
denotes the space of Jacobi cusp forms of weight k, level N, and index m.
Given a primitive matrix
 $S = {\left (\begin {array}{@{}cc@{}}a&b/2\\b/2&c\end {array}\right )} \in \Lambda _2$
(i.e.,
$S = {\left (\begin {array}{@{}cc@{}}a&b/2\\b/2&c\end {array}\right )} \in \Lambda _2$
(i.e.,
![]() $\gcd (a,b,c)=1$
), we let
$\gcd (a,b,c)=1$
), we let
![]() ${\mathcal P}(S)$
denote the set of primes of the form
${\mathcal P}(S)$
denote the set of primes of the form
![]() $ax^2+bxy+cy^2$
. The set
$ax^2+bxy+cy^2$
. The set
![]() ${\mathcal P}(S)$
is infinite; indeed, by [Reference Iwaniec28, Theorem 1(i)],
${\mathcal P}(S)$
is infinite; indeed, by [Reference Iwaniec28, Theorem 1(i)],
 $$ \begin{align} \lvert\{p \in {\mathcal P}(S): p \le X\}\rvert \gg_S \frac{X}{\log X}. \end{align} $$
$$ \begin{align} \lvert\{p \in {\mathcal P}(S): p \le X\}\rvert \gg_S \frac{X}{\log X}. \end{align} $$
For each prime p dividing N, define the operator
![]() $U(p)$
acting on the space
$U(p)$
acting on the space
 $S_k(\Gamma ^{(2)}_0(N))$
via
$S_k(\Gamma ^{(2)}_0(N))$
via
Lemma 5.1. Let
![]() $k>2$
be even and N be square-free. Let
$k>2$
be even and N be square-free. Let
 $F \in S_k(\Gamma ^{(2)}_0(N))$
be an eigenfunction of the
$F \in S_k(\Gamma ^{(2)}_0(N))$
be an eigenfunction of the
![]() $U(p)$
operator for each prime
$U(p)$
operator for each prime
![]() $p\mid N$
(note that if
$p\mid N$
(note that if
![]() $N=1$
, this condition is trivially true).
$N=1$
, this condition is trivially true).
-
i) Then there exists
 $S_0 = {\left (\begin {array}{@{}cc@{}}a&b/2\\b/2&c\end {array}\right )} \in \Lambda _2$
such that
$S_0 = {\left (\begin {array}{@{}cc@{}}a&b/2\\b/2&c\end {array}\right )} \in \Lambda _2$
such that
 $a(F,S_0) \neq 0$
and
$a(F,S_0) \neq 0$
and
 $d_0 = b^2-4ac$
is odd and square-free (and hence
$d_0 = b^2-4ac$
is odd and square-free (and hence
 $S_0$
is fundamental).
$S_0$
is fundamental). -
ii) Let
 $S_0, d_0$
be as before and let
$S_0, d_0$
be as before and let
 $p \nmid 2Nd_0$
be a prime such that
$p \nmid 2Nd_0$
be a prime such that
 $p \in {\mathcal P}(S_0)$
. Put Then
$p \in {\mathcal P}(S_0)$
. Put Then $$ \begin{align*} h_p(z) = \sum_{m=1}^\infty a(m) e^{2 \pi i m z}, \qquad \text{where } a(m) = \sum_{\substack{0 \le \mu \le 2p-1 \\ \mu^2 \equiv -m \! \! \! \! \pmod{4p}}} a\left(F, {\left(\begin{array}{@{}cc@{}}\frac{m+\mu^2}{4p}&\frac{\mu}{2}\\\frac{\mu}{2}&p\end{array}\right)} \right). \end{align*} $$
$$ \begin{align*} h_p(z) = \sum_{m=1}^\infty a(m) e^{2 \pi i m z}, \qquad \text{where } a(m) = \sum_{\substack{0 \le \mu \le 2p-1 \\ \mu^2 \equiv -m \! \! \! \! \pmod{4p}}} a\left(F, {\left(\begin{array}{@{}cc@{}}\frac{m+\mu^2}{4p}&\frac{\mu}{2}\\\frac{\mu}{2}&p\end{array}\right)} \right). \end{align*} $$
 $0 \neq h_p \in S^+_{k-\frac {1}{2}}(4pN)$
. Furthermore, for each
$0 \neq h_p \in S^+_{k-\frac {1}{2}}(4pN)$
. Furthermore, for each
 $m>0$
such that
$m>0$
such that
 $\gcd (m, 4p)=1$
, (51)where
$\gcd (m, 4p)=1$
, (51)where $$ \begin{align} a(m) = 2 a\left(F, {\left(\begin{array}{@{}cc@{}}\frac{m+\mu_0^2}{4p}&\frac{\mu_0}{2}\\\frac{\mu_0}{2}&p\end{array}\right)} \right), \end{align} $$
$$ \begin{align} a(m) = 2 a\left(F, {\left(\begin{array}{@{}cc@{}}\frac{m+\mu_0^2}{4p}&\frac{\mu_0}{2}\\\frac{\mu_0}{2}&p\end{array}\right)} \right), \end{align} $$
 $\mu _0$
is any integer satisfying
$\mu _0$
is any integer satisfying
 $\mu _0^2 \equiv -m \pmod {4p}$
; if no such
$\mu _0^2 \equiv -m \pmod {4p}$
; if no such
 $\mu _0$
exists, then
$\mu _0$
exists, then
 $a(m)=0$
.
$a(m)=0$
.
Proof. The claim that there exists
 $S_0 = {\left (\begin {array}{@{}cc@{}}a&b/2\\b/2&c\end {array}\right )} \in \Lambda _2$
such that
$S_0 = {\left (\begin {array}{@{}cc@{}}a&b/2\\b/2&c\end {array}\right )} \in \Lambda _2$
such that
![]() $a(F, S_0)\neq 0$
and
$a(F, S_0)\neq 0$
and
![]() $d_0 = b^2-4ac$
is odd and square-free follows from [Reference Schmidt58, Theorem 2.2].
$d_0 = b^2-4ac$
is odd and square-free follows from [Reference Schmidt58, Theorem 2.2].
Now let
![]() $p \in {\mathcal P}(S_0)$
,
$p \in {\mathcal P}(S_0)$
,
![]() $p \nmid 2Nd_0$
. The fact that
$p \nmid 2Nd_0$
. The fact that
 $h_p \in S_{k-\frac {1}{2}}(4pN)$
follows from
$h_p \in S_{k-\frac {1}{2}}(4pN)$
follows from
 $\phi _{p} \in J_{k,p}^{\text {cusp}}(N) $
and [Reference Manickam and Ramakrishnan41, Theorem 4.8]; by definition,
$\phi _{p} \in J_{k,p}^{\text {cusp}}(N) $
and [Reference Manickam and Ramakrishnan41, Theorem 4.8]; by definition,
![]() $h_p$
belongs to the Kohnen plus space. Next we prove equation (51). Let
$h_p$
belongs to the Kohnen plus space. Next we prove equation (51). Let
![]() $\gcd (m, 4p)=1$
. Observe that the sum
$\gcd (m, 4p)=1$
. Observe that the sum
 $\sum _{\substack {0 \le \mu \le 2p-1 \\ \mu ^2 \equiv -m \pmod {4p}}}$
is nonempty if and only if
$\sum _{\substack {0 \le \mu \le 2p-1 \\ \mu ^2 \equiv -m \pmod {4p}}}$
is nonempty if and only if
![]() $-m$
is a square modulo
$-m$
is a square modulo
![]() $4p$
, in which case the sum has exactly two terms. Indeed, we get
$4p$
, in which case the sum has exactly two terms. Indeed, we get
 $$ \begin{align} a(m) = a\left(F, {\left(\begin{array}{@{}cc@{}}\frac{m+\mu_0^2}{4p}&\frac{\mu_0}{2}\\\frac{\mu_0}{2}&p\end{array}\right)}\right) + a\left(F, {\left(\begin{array}{@{}cc@{}}\frac{m+\mu_1^2}{4p}&\frac{\mu_1}{2}\\\frac{\mu_1}{2}&p\end{array}\right)}\right), \end{align} $$
$$ \begin{align} a(m) = a\left(F, {\left(\begin{array}{@{}cc@{}}\frac{m+\mu_0^2}{4p}&\frac{\mu_0}{2}\\\frac{\mu_0}{2}&p\end{array}\right)}\right) + a\left(F, {\left(\begin{array}{@{}cc@{}}\frac{m+\mu_1^2}{4p}&\frac{\mu_1}{2}\\\frac{\mu_1}{2}&p\end{array}\right)}\right), \end{align} $$
where
![]() $0 \le \mu _0 \le 2p-1$
satisfies
$0 \le \mu _0 \le 2p-1$
satisfies
![]() $\mu _0^2 \equiv -m \pmod {4p}$
and
$\mu _0^2 \equiv -m \pmod {4p}$
and
![]() $\mu _1 = 2p-\mu _0$
. Using equations (47) and (52) and the identity
$\mu _1 = 2p-\mu _0$
. Using equations (47) and (52) and the identity
 ${\left (\begin {array}{@{}cc@{}}1&-1\\0&-1\end {array}\right )} {\left (\begin {array}{@{}cc@{}}\frac {m+\mu _0^2}{4p}&\frac {\mu _0}{2}\\\frac {\mu _0}{2}&p\end {array}\right )}{\left (\begin {array}{@{}cc@{}}1&0\\-1&-1\end {array}\right )} = {\left (\begin {array}{@{}cc@{}}\frac {m+\mu _1^2}{4p}&\frac {\mu _1}{2}\\\frac {\mu _1}{2}&p\end {array}\right )}$
, we obtain equation (51).
${\left (\begin {array}{@{}cc@{}}1&-1\\0&-1\end {array}\right )} {\left (\begin {array}{@{}cc@{}}\frac {m+\mu _0^2}{4p}&\frac {\mu _0}{2}\\\frac {\mu _0}{2}&p\end {array}\right )}{\left (\begin {array}{@{}cc@{}}1&0\\-1&-1\end {array}\right )} = {\left (\begin {array}{@{}cc@{}}\frac {m+\mu _1^2}{4p}&\frac {\mu _1}{2}\\\frac {\mu _1}{2}&p\end {array}\right )}$
, we obtain equation (51).
It remains to show
![]() $h_p \neq 0$
, for which we will show that
$h_p \neq 0$
, for which we will show that
![]() $a(-d_0)\neq 0$
. Let
$a(-d_0)\neq 0$
. Let
![]() $x_0, y_0$
be integers such that
$x_0, y_0$
be integers such that
![]() $cx_0^2 + bx_0y_0 + ay_0^2=p$
. Since
$cx_0^2 + bx_0y_0 + ay_0^2=p$
. Since
![]() $\gcd (x_0, y_0) = 1$
, we may pick integers
$\gcd (x_0, y_0) = 1$
, we may pick integers
![]() $x_1, y_1$
such that
$x_1, y_1$
such that
 $A= {\left (\begin {array}{@{}cc@{}}y_1&y_0\\x_1&x_0\end {array}\right )} \in {\mathrm{SL}}_2({\mathbb Z}).$
Then
$A= {\left (\begin {array}{@{}cc@{}}y_1&y_0\\x_1&x_0\end {array}\right )} \in {\mathrm{SL}}_2({\mathbb Z}).$
Then
![]() $S' = {}^t\!{A}SA$
is
$S' = {}^t\!{A}SA$
is
![]() ${\mathrm{SL}}_2({\mathbb Z})$
-equivalent to
${\mathrm{SL}}_2({\mathbb Z})$
-equivalent to
![]() $S_0$
and has the form
$S_0$
and has the form
 $S'={\left (\begin {array}{@{}cc@{}}\frac {-d_0+\mu _0^2}{4p}&\frac {\mu _0}{2}\\\frac {\mu _0}{2}&p\end {array}\right )} \in \Lambda _2$
. By equation (47),
$S'={\left (\begin {array}{@{}cc@{}}\frac {-d_0+\mu _0^2}{4p}&\frac {\mu _0}{2}\\\frac {\mu _0}{2}&p\end {array}\right )} \in \Lambda _2$
. By equation (47),
![]() $a(F,S') \neq 0$
since
$a(F,S') \neq 0$
since
![]() $a(F, S_0) \neq 0$
. Hence by equation (51),
$a(F, S_0) \neq 0$
. Hence by equation (51),
![]() $a(-d_0) = 2 a(F,S') \neq 0$
.
$a(-d_0) = 2 a(F,S') \neq 0$
.
5.3. Proofs of Theorems A and B
We are now ready to prove Theorems A and B in slightly stronger forms.
Theorem 5.2. Let
 $F \in S_k(\Gamma ^{(2)}_0(N))$
with
$F \in S_k(\Gamma ^{(2)}_0(N))$
with
![]() $k> 2$
even and N odd and square-free. Assume that F is an eigenfunction of the
$k> 2$
even and N odd and square-free. Assume that F is an eigenfunction of the
![]() $U(p)$
operator for each prime
$U(p)$
operator for each prime
![]() $p\mid N$
, and that F has real Fourier coefficients. Then there exists a set
$p\mid N$
, and that F has real Fourier coefficients. Then there exists a set
![]() ${\mathcal P}$
of primes satisfying
${\mathcal P}$
of primes satisfying
 $\lvert \{p \in {\mathcal P}: p \le X\}\rvert \gg _F \frac {X}{\log X}$
such that given
$\lvert \{p \in {\mathcal P}: p \le X\}\rvert \gg _F \frac {X}{\log X}$
such that given
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $p \in {\mathcal P}$
, there exist
$p \in {\mathcal P}$
, there exist
![]() $M\ge 2$
(depending only on F and p) and
$M\ge 2$
(depending only on F and p) and
![]() $X_0\ge 1$
(depending on F, p, and
$X_0\ge 1$
(depending on F, p, and
![]() $\varepsilon $
) such that for all
$\varepsilon $
) such that for all
![]() $X \ge X_0$
, there are
$X \ge X_0$
, there are
![]() $r_X \ge X^{1-\varepsilon }$
matrices
$r_X \ge X^{1-\varepsilon }$
matrices
![]() $S_1, S_2, \dotsc , S_{r_{X}} \in \Lambda _2$
satisfying the following:
$S_1, S_2, \dotsc , S_{r_{X}} \in \Lambda _2$
satisfying the following:
-
i)
 $X \le \lvert {\mathrm{disc}}(S_1)\rvert < \lvert {\mathrm{disc}}(S_2)\rvert < \dotsb < \left \lvert {\mathrm{disc}}\left (S_{r_X}\right )\right \rvert \le MX$
.
$X \le \lvert {\mathrm{disc}}(S_1)\rvert < \lvert {\mathrm{disc}}(S_2)\rvert < \dotsb < \left \lvert {\mathrm{disc}}\left (S_{r_X}\right )\right \rvert \le MX$
. -
ii) For each
 $1\le i \le r_X$
,
$1\le i \le r_X$
,
 $S_i = {\left (\begin {array}{@{}cc@{}}*&*\\\ast &p\end {array}\right )}$
, and
$S_i = {\left (\begin {array}{@{}cc@{}}*&*\\\ast &p\end {array}\right )}$
, and
 ${\mathrm{disc}}(S_i)$
is a square-free integer coprime to
${\mathrm{disc}}(S_i)$
is a square-free integer coprime to
 $2N$
.
$2N$
. -
iii) For each
 $1\le i \le r_X-1$
,
$1\le i \le r_X-1$
,
 $a(F, S_{i})a(F, S_{i+1})<0$
.
$a(F, S_{i})a(F, S_{i+1})<0$
.
Proof. Using Lemma 5.1, we fix a fundamental matrix
![]() $S_0$
such that
$S_0$
such that
![]() $a(F,S_0) \neq 0$
. Take
$a(F,S_0) \neq 0$
. Take
![]() ${\mathcal P} = {\mathcal P}(S_0)$
; then the estimate
${\mathcal P} = {\mathcal P}(S_0)$
; then the estimate
 $\lvert \{p \in {\mathcal P}: p \le X\}\rvert \gg \frac {X}{\log X}$
follows from the bound (49). Given any
$\lvert \{p \in {\mathcal P}: p \le X\}\rvert \gg \frac {X}{\log X}$
follows from the bound (49). Given any
![]() $p \in {\mathcal P}$
, let
$p \in {\mathcal P}$
, let
![]() $f=h_{p}$
be as in Lemma 5.1, so that
$f=h_{p}$
be as in Lemma 5.1, so that
 $0 \neq f \in S^+_{k-\frac {1}{2}}(4pN)$
and the coefficients of f are all real, since the coefficients of F are.
$0 \neq f \in S^+_{k-\frac {1}{2}}(4pN)$
and the coefficients of f are all real, since the coefficients of F are.
By Theorem 3.1, there exists
![]() $M\ge 2$
such that for any
$M\ge 2$
such that for any
![]() $\varepsilon>0$
, the sequence
$\varepsilon>0$
, the sequence
 $\left \{ a(f,n)\mu ^2(n) \right \}_{\substack {X \leq n \leq MX \\ \left (n,2N\right )=1}}$
has
$\left \{ a(f,n)\mu ^2(n) \right \}_{\substack {X \leq n \leq MX \\ \left (n,2N\right )=1}}$
has
![]() $\ge C_{f,M,\varepsilon } X^{1-\varepsilon /2}$
sign changes for some constant
$\ge C_{f,M,\varepsilon } X^{1-\varepsilon /2}$
sign changes for some constant
![]() $C_{f,M,\varepsilon }$
. Pick
$C_{f,M,\varepsilon }$
. Pick
![]() $X_0 \ge 1$
such that for all
$X_0 \ge 1$
such that for all
![]() $X \ge X_0$
we have
$X \ge X_0$
we have
 $X^{\varepsilon /2} \ge \frac {1}{C_{f,M,\varepsilon }}$
. Then for all
$X^{\varepsilon /2} \ge \frac {1}{C_{f,M,\varepsilon }}$
. Then for all
![]() $X \ge X_0$
, there exists
$X \ge X_0$
, there exists
![]() $r_X \ge X^{1-\varepsilon }$
and an increasing sequence
$r_X \ge X^{1-\varepsilon }$
and an increasing sequence
![]() $(n_i)_{1 \le i \le r_X}$
of odd square-free integers satisfying
$(n_i)_{1 \le i \le r_X}$
of odd square-free integers satisfying
![]() $a(f,n_i) a(f,n_{i+1}) < 0$
. For each
$a(f,n_i) a(f,n_{i+1}) < 0$
. For each
![]() $n_i$
as discussed, equation (51) tells us that
$n_i$
as discussed, equation (51) tells us that
![]() $a(f,n_i) = 2 a(F,S_i)$
for some
$a(f,n_i) = 2 a(F,S_i)$
for some
 $S_i = {\left (\begin {array}{@{}cc@{}}*&*\\\ast &p\end {array}\right )} \in \Lambda _2$
with
$S_i = {\left (\begin {array}{@{}cc@{}}*&*\\\ast &p\end {array}\right )} \in \Lambda _2$
with
![]() $\lvert {\mathrm{disc}}(S_i)\rvert = n_i$
. This completes the proof.
$\lvert {\mathrm{disc}}(S_i)\rvert = n_i$
. This completes the proof.
Theorem 5.3. Let
 $F \in S_k(\Gamma ^{(2)}_0(N))$
with
$F \in S_k(\Gamma ^{(2)}_0(N))$
with
![]() $k>2$
even and N odd and square-free. Assume that F is an eigenfunction of the
$k>2$
even and N odd and square-free. Assume that F is an eigenfunction of the
![]() $U(p)$
operator for each prime
$U(p)$
operator for each prime
![]() $p\mid N$
. Then there exists a set
$p\mid N$
. Then there exists a set
![]() ${\mathcal P}$
of primes satisfying
${\mathcal P}$
of primes satisfying
 $\lvert \{p \in {\mathcal P}: p \le X\}\rvert \gg _F \frac {X}{\log X}$
such that given
$\lvert \{p \in {\mathcal P}: p \le X\}\rvert \gg _F \frac {X}{\log X}$
such that given
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $p \in {\mathcal P}$
, one can find
$p \in {\mathcal P}$
, one can find
![]() $X_0\ge 1$
(depending on F, p, and
$X_0\ge 1$
(depending on F, p, and
![]() $\varepsilon $
) such that for all
$\varepsilon $
) such that for all
![]() $X \ge X_0$
, there are
$X \ge X_0$
, there are
![]() $r_X \ge X^{1-\varepsilon }$
matrices
$r_X \ge X^{1-\varepsilon }$
matrices
![]() $S_1, S_2, \dotsc , S_{r_{X}} \in \Lambda _2$
satisfying the following:
$S_1, S_2, \dotsc , S_{r_{X}} \in \Lambda _2$
satisfying the following:
-
i) For each
 $1\le i \le r_X$
,
$1\le i \le r_X$
,
 $S_i = {\left (\begin {array}{@{}cc@{}}*&*\\\ast &p\end {array}\right )}$
, and
$S_i = {\left (\begin {array}{@{}cc@{}}*&*\\\ast &p\end {array}\right )}$
, and
 ${\mathrm{disc}}(S_i)$
is a square-free integer coprime to
${\mathrm{disc}}(S_i)$
is a square-free integer coprime to
 $2N$
.
$2N$
. -
ii)
 $X \le \lvert {\mathrm{disc}}(S_1)\rvert < \lvert {\mathrm{disc}}(S_2)\rvert < \dotsb < \left \lvert {\mathrm{disc}}\left (S_{r_X}\right )\right \rvert \le 2X$
.
$X \le \lvert {\mathrm{disc}}(S_1)\rvert < \lvert {\mathrm{disc}}(S_2)\rvert < \dotsb < \left \lvert {\mathrm{disc}}\left (S_{r_X}\right )\right \rvert \le 2X$
. -
iii) For each
 $1\le i \le r_X$
,
$1\le i \le r_X$
,
 $\lvert a(F,S_i)\rvert \ge \lvert {\mathrm{disc}}(S_i)\rvert ^{\frac {k}2 - \frac 34} \exp \left (\frac {1}{82} \sqrt {\frac {\log \lvert {\mathrm{disc}}\left (S_i\right )\rvert }{\log \log \lvert {\mathrm{disc}}\left (S_i\right )\rvert }} \right ).$
$\lvert a(F,S_i)\rvert \ge \lvert {\mathrm{disc}}(S_i)\rvert ^{\frac {k}2 - \frac 34} \exp \left (\frac {1}{82} \sqrt {\frac {\log \lvert {\mathrm{disc}}\left (S_i\right )\rvert }{\log \log \lvert {\mathrm{disc}}\left (S_i\right )\rvert }} \right ).$
5.4. L-functions of Siegel cusp forms
For the rest of this section, we assume that
![]() $k>2$
.
$k>2$
.
Given an irreducible cuspidal automorphic representation
![]() $\pi $
of
$\pi $
of
![]() ${\mathrm{GSp}}_4({\mathbb A})$
, we let
${\mathrm{GSp}}_4({\mathbb A})$
, we let
![]() $L(s, \pi )$
denote the associated degree
$L(s, \pi )$
denote the associated degree
![]() $4\ L$
-function (known as the ‘spin’ L-function). Furthermore, we let
$4\ L$
-function (known as the ‘spin’ L-function). Furthermore, we let
![]() $L(s, \mathrm {std}(\pi ))$
denote the associated degree
$L(s, \mathrm {std}(\pi ))$
denote the associated degree
![]() $5\ L$
-function (the ‘standard’ L-function) and
$5\ L$
-function (the ‘standard’ L-function) and
![]() $L(s, \mathrm {ad}(\pi ))$
denote the associated degree
$L(s, \mathrm {ad}(\pi ))$
denote the associated degree
![]() $10\ L$
-function (the ‘adjoint’ L-function). Each of these L-functions is defined as an Euler product with the local L-factor at each prime (including the ramified primes) constructed via the associated representation of the dual group
$10\ L$
-function (the ‘adjoint’ L-function). Each of these L-functions is defined as an Euler product with the local L-factor at each prime (including the ramified primes) constructed via the associated representation of the dual group
![]() ${\mathrm{GSp}}_4({\mathbb C})$
using the local Langlands correspondence (which is known for
${\mathrm{GSp}}_4({\mathbb C})$
using the local Langlands correspondence (which is known for
![]() ${\mathrm{GSp}}_4$
by the work of Gan and Takeda [Reference Gun, Kohnen and Soundararajan19]). More precisely, for
${\mathrm{GSp}}_4$
by the work of Gan and Takeda [Reference Gun, Kohnen and Soundararajan19]). More precisely, for
![]() $n=4,5,10$
, let
$n=4,5,10$
, let
![]() $\rho _n$
denote the irreducible n-dimensional representation of
$\rho _n$
denote the irreducible n-dimensional representation of
![]() ${\mathrm{GSp}}_4({\mathbb C})$
given as follows:
${\mathrm{GSp}}_4({\mathbb C})$
given as follows:
![]() $\rho _4$
is the inclusion
$\rho _4$
is the inclusion
![]() ${\mathrm{GSp}}_4({\mathbb C}) \hookrightarrow {\mathrm{GL}}_4({\mathbb C})$
,
${\mathrm{GSp}}_4({\mathbb C}) \hookrightarrow {\mathrm{GL}}_4({\mathbb C})$
,
![]() $\rho _5$
is the map defined in [Reference Radziwiłł and Soundararajan52, A.7], and
$\rho _5$
is the map defined in [Reference Radziwiłł and Soundararajan52, A.7], and
![]() $\rho _{10}$
is the adjoint representation of
$\rho _{10}$
is the adjoint representation of
![]() ${\mathrm{GSp}}_4({\mathbb C})$
on the Lie algebra of
${\mathrm{GSp}}_4({\mathbb C})$
on the Lie algebra of
![]() $\mathrm {Sp}_4({\mathbb C})$
. Then
$\mathrm {Sp}_4({\mathbb C})$
. Then
![]() $L(s, \pi )$
,
$L(s, \pi )$
,
![]() $L(s, \mathrm {std}(\pi ))$
, and
$L(s, \mathrm {std}(\pi ))$
, and
![]() $L(s, \mathrm {ad}(\pi ))$
correspond to the representations
$L(s, \mathrm {ad}(\pi ))$
correspond to the representations
![]() $\rho _4$
,
$\rho _4$
,
![]() $\rho _5$
, and
$\rho _5$
, and
![]() $\rho _{10}$
, respectively.
$\rho _{10}$
, respectively.
We say that an element F of
 $S_k(\Gamma ^{(2)}_0(N))$
gives rise to an irreducible representation if its adelization (in the sense of [Reference Böcherer and Das5
Reference Bump and Ginzburg7, §3]) generates an irreducible cuspidal automorphic representation of
$S_k(\Gamma ^{(2)}_0(N))$
gives rise to an irreducible representation if its adelization (in the sense of [Reference Böcherer and Das5
Reference Bump and Ginzburg7, §3]) generates an irreducible cuspidal automorphic representation of
![]() ${\mathrm{GSp}}_4({\mathbb A})$
. The automorphic representation associated to any such F is of trivial central character and hence may be viewed as an automorphic representation of
${\mathrm{GSp}}_4({\mathbb A})$
. The automorphic representation associated to any such F is of trivial central character and hence may be viewed as an automorphic representation of
![]() ${\mathrm{PGSp}}_4({\mathbb A}) \simeq {\mathrm{SO}}_5({\mathbb A})$
. It can be checked [Reference Böcherer and Das5
Reference Bump and Ginzburg7, Proposition 3.11] that if F gives rise to an irreducible representation, then F is an eigenform of the local Hecke algebras at all primes not dividing N. In addition, we say that such an F is factorizable if its adelization corresponds to a factorizable vector in the representation generated.
${\mathrm{PGSp}}_4({\mathbb A}) \simeq {\mathrm{SO}}_5({\mathbb A})$
. It can be checked [Reference Böcherer and Das5
Reference Bump and Ginzburg7, Proposition 3.11] that if F gives rise to an irreducible representation, then F is an eigenform of the local Hecke algebras at all primes not dividing N. In addition, we say that such an F is factorizable if its adelization corresponds to a factorizable vector in the representation generated.
We say that an irreducible cuspidal automorphic representation
![]() $\pi $
of
$\pi $
of
![]() ${\mathrm{GSp}}_4({\mathbb A})$
arises from
${\mathrm{GSp}}_4({\mathbb A})$
arises from
 $S_k(\Gamma ^{(2)}_0(N))$
if there exists
$S_k(\Gamma ^{(2)}_0(N))$
if there exists
 $F \in S_k(\Gamma ^{(2)}_0(N))$
whose adelization generates
$F \in S_k(\Gamma ^{(2)}_0(N))$
whose adelization generates
![]() $V_\pi $
(in which case, by definition, F gives rise to the irreducible representation
$V_\pi $
(in which case, by definition, F gives rise to the irreducible representation
![]() $\pi $
, which therefore must be of trivial central character by the previous comments). We say that an irreducible cuspidal automorphic representation
$\pi $
, which therefore must be of trivial central character by the previous comments). We say that an irreducible cuspidal automorphic representation
![]() $\pi $
of
$\pi $
of
![]() ${\mathrm{GSp}}_4({\mathbb A})$
is ‘CAP’ if it is nearly equivalent to a constituent of a global induced representation of a proper parabolic subgroup of
${\mathrm{GSp}}_4({\mathbb A})$
is ‘CAP’ if it is nearly equivalent to a constituent of a global induced representation of a proper parabolic subgroup of
![]() ${\mathrm{GSp}}_4({\mathbb A})$
. If a CAP
${\mathrm{GSp}}_4({\mathbb A})$
. If a CAP
![]() $\pi $
arises from
$\pi $
arises from
 $S_k(\Gamma ^{(2)}_0(N))$
, then by [Reference Pitale and Schmidt47, Corollary 4.5] it is associated to the Siegel parabolic (i.e., it is of Saito–Kurokawa type). Such a
$S_k(\Gamma ^{(2)}_0(N))$
, then by [Reference Pitale and Schmidt47, Corollary 4.5] it is associated to the Siegel parabolic (i.e., it is of Saito–Kurokawa type). Such a
![]() $\pi $
is nontempered at almost all primes (in particular, it violates the Ramanujan conjecture). On the other hand, if
$\pi $
is nontempered at almost all primes (in particular, it violates the Ramanujan conjecture). On the other hand, if
![]() $\pi $
arises from
$\pi $
arises from
 $S_k(\Gamma ^{(2)}_0(N))$
and is not CAP, then
$S_k(\Gamma ^{(2)}_0(N))$
and is not CAP, then
![]() $\pi $
satisfies the Ramanujan conjecture by a famous result of Weissauer [Reference Weissauer68, Theorem 3.3].
$\pi $
satisfies the Ramanujan conjecture by a famous result of Weissauer [Reference Weissauer68, Theorem 3.3].
Thus, the space
 $S_k(\Gamma ^{(2)}_0(N))$
has a natural decomposition into orthogonal subspaces
$S_k(\Gamma ^{(2)}_0(N))$
has a natural decomposition into orthogonal subspaces
 $$ \begin{align*} S_k\left(\Gamma^{(2)}_0(N)\right)=S_k\left(\Gamma^{(2)}_0(N)\right)^{\textrm{CAP}} \oplus S_k\left(\Gamma^{(2)}_0(N)\right)^{ \rm T}, \end{align*} $$
$$ \begin{align*} S_k\left(\Gamma^{(2)}_0(N)\right)=S_k\left(\Gamma^{(2)}_0(N)\right)^{\textrm{CAP}} \oplus S_k\left(\Gamma^{(2)}_0(N)\right)^{ \rm T}, \end{align*} $$
where
 $S_k(\Gamma ^{(2)}_0(N))^{\mathrm{CAP}}$
is spanned by forms F which give rise to irreducible representations of Saito–Kurokawa type, and
$S_k(\Gamma ^{(2)}_0(N))^{\mathrm{CAP}}$
is spanned by forms F which give rise to irreducible representations of Saito–Kurokawa type, and
 $S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
is its orthogonal complement, spanned by forms F which give rise to irreducible representations that are not of Saito–Kurokawa type. Furthermore, one can get a basis of each of the spaces
$S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
is its orthogonal complement, spanned by forms F which give rise to irreducible representations that are not of Saito–Kurokawa type. Furthermore, one can get a basis of each of the spaces
 $S_k(\Gamma ^{(2)}_0(N))^{\mathrm{CAP}}$
and
$S_k(\Gamma ^{(2)}_0(N))^{\mathrm{CAP}}$
and
 $S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
in terms of factorizable forms. We refer the reader to [Reference Dickson, Pitale, Saha and Schmidt15, §§3.1 and 3.2] for further comments related to the foregoing discussion.
$S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
in terms of factorizable forms. We refer the reader to [Reference Dickson, Pitale, Saha and Schmidt15, §§3.1 and 3.2] for further comments related to the foregoing discussion.
If
![]() $\pi $
arises from
$\pi $
arises from
 $S_k(\Gamma ^{(2)}_0(N))$
and is of Saito–Kurokawa type, then there exist a representation
$S_k(\Gamma ^{(2)}_0(N))$
and is of Saito–Kurokawa type, then there exist a representation
![]() $\pi _0$
of
$\pi _0$
of
![]() ${\mathrm{GL}}_2({\mathbb A})$
and a Dirichlet character
${\mathrm{GL}}_2({\mathbb A})$
and a Dirichlet character
![]() $\chi _0$
satisfying
$\chi _0$
satisfying
![]() $\chi _0^2=1$
such that
$\chi _0^2=1$
such that
![]() $L^N(s, \pi ) = L^N(s, \pi _0) L^N(s+1/2, \chi _0) L^N(s-1/2, \chi _0)$
. Additionally, if N is square-free, then only
$L^N(s, \pi ) = L^N(s, \pi _0) L^N(s+1/2, \chi _0) L^N(s-1/2, \chi _0)$
. Additionally, if N is square-free, then only
![]() $\chi _0=1$
is possible, by a well-known result of Borel [Reference Böcherer8], and so in this case we have
$\chi _0=1$
is possible, by a well-known result of Borel [Reference Böcherer8], and so in this case we have
![]() $L^N(s, \pi ) = L^N(s, \pi _0) \zeta ^N(s+1/2) \zeta ^N(s-1/2)$
. There exists another typical situation where the L-function factors: we say that a
$L^N(s, \pi ) = L^N(s, \pi _0) \zeta ^N(s+1/2) \zeta ^N(s-1/2)$
. There exists another typical situation where the L-function factors: we say that a
![]() $\pi $
arising from
$\pi $
arising from
 $S_k(\Gamma ^{(2)}_0(N))$
is of Yoshida type if there are representations
$S_k(\Gamma ^{(2)}_0(N))$
is of Yoshida type if there are representations
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
of
$\pi _2$
of
![]() ${\mathrm{GL}}_2({\mathbb A})$
such that
${\mathrm{GL}}_2({\mathbb A})$
such that
![]() $L(s, \pi ) = L(s, \pi _1) L(s, \pi _2)$
; in this case (after possibly swapping
$L(s, \pi ) = L(s, \pi _1) L(s, \pi _2)$
; in this case (after possibly swapping
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
),
$\pi _2$
),
![]() $\pi _1$
arises from a classical holomorphic newform of weight
$\pi _1$
arises from a classical holomorphic newform of weight
![]() $2$
and
$2$
and
![]() $\pi _2$
arises from a classical holomorphic newform of weight
$\pi _2$
arises from a classical holomorphic newform of weight
![]() $2k-2$
(see [Reference Böcherer and Das5
Reference Bump and Ginzburg7, §4] for more details). We let
$2k-2$
(see [Reference Böcherer and Das5
Reference Bump and Ginzburg7, §4] for more details). We let
 $S_k(\Gamma ^{(2)}_0(N))^{ \rm Y}$
denote the subspace of
$S_k(\Gamma ^{(2)}_0(N))^{ \rm Y}$
denote the subspace of
 $S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
spanned by forms which give rise to an irreducible representation of Yoshida type, and let
$S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
spanned by forms which give rise to an irreducible representation of Yoshida type, and let
 $S_k(\Gamma ^{(2)}_0(N))^{ \rm G}$
– which represents the general type – denote the orthogonal complement of
$S_k(\Gamma ^{(2)}_0(N))^{ \rm G}$
– which represents the general type – denote the orthogonal complement of
 $S_k(\Gamma ^{(2)}_0(N))^{ \rm Y}$
in
$S_k(\Gamma ^{(2)}_0(N))^{ \rm Y}$
in
 $S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
. So we get the following key orthogonal decomposition into subspaces:
$S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
. So we get the following key orthogonal decomposition into subspaces:
 $$ \begin{align} S_k\left(\Gamma^{(2)}_0(N)\right)=S_k\left(\Gamma^{(2)}_0(N)\right)^{\textrm{CAP}} \oplus S_k\left(\Gamma^{(2)}_0(N)\right)^{ \rm Y} \oplus S_k\left(\Gamma^{(2)}_0(N)\right)^{ \rm G}. \end{align} $$
$$ \begin{align} S_k\left(\Gamma^{(2)}_0(N)\right)=S_k\left(\Gamma^{(2)}_0(N)\right)^{\textrm{CAP}} \oplus S_k\left(\Gamma^{(2)}_0(N)\right)^{ \rm Y} \oplus S_k\left(\Gamma^{(2)}_0(N)\right)^{ \rm G}. \end{align} $$
In the notation of [Reference Shahidi59], the three subspaces on the right-hand side correspond to the global Arthur packets of type (P), (Y), and (G), respectively. In the sequel we will be mostly concerned with the space
 $S_k(\Gamma ^{(2)}_0(N))^{ \rm G}$
, because the other two spaces are easier to handle. The following proposition collects together some relevant facts about the associated L-functions that follow from the work of Arthur [Reference Andrianov2]:
$S_k(\Gamma ^{(2)}_0(N))^{ \rm G}$
, because the other two spaces are easier to handle. The following proposition collects together some relevant facts about the associated L-functions that follow from the work of Arthur [Reference Andrianov2]:
Proposition 5.4. Suppose that
 $F \in S_k(\Gamma ^{(2)}_0(N))^{ \rm G}$
gives rise to an irreducible representation
$F \in S_k(\Gamma ^{(2)}_0(N))^{ \rm G}$
gives rise to an irreducible representation
![]() $\pi $
.
$\pi $
.
-
i) The representation
 $\pi $
has a strong functorial lifting to an irreducible cuspidal automorphic representation
$\pi $
has a strong functorial lifting to an irreducible cuspidal automorphic representation
 $\Pi _4$
of
$\Pi _4$
of
 ${\mathrm{GL}}_4({\mathbb A})$
. In particular, if
${\mathrm{GL}}_4({\mathbb A})$
. In particular, if
 $\sigma $
is any irreducible automorphic representation of
$\sigma $
is any irreducible automorphic representation of
 ${\mathrm{GL}}_n({\mathbb A})$
, then we have an equality of degree
${\mathrm{GL}}_n({\mathbb A})$
, then we have an equality of degree
 $4n$
Rankin–Selberg L-functions
$4n$
Rankin–Selberg L-functions
 $L(s, \pi \times \sigma )= L(s, \Pi _4 \times \sigma )$
, and therefore
$L(s, \pi \times \sigma )= L(s, \Pi _4 \times \sigma )$
, and therefore
 $L(s, \pi \times \sigma )$
satisfies the usual propertiesFootnote
6
of an L-function. If
$L(s, \pi \times \sigma )$
satisfies the usual propertiesFootnote
6
of an L-function. If
 $n \le 3$
, then
$n \le 3$
, then
 $L(s, \pi \times \sigma )$
is entire.
$L(s, \pi \times \sigma )$
is entire. -
ii) The representation
 $\pi $
has a strong functorial lifting to an irreducible automorphic representation
$\pi $
has a strong functorial lifting to an irreducible automorphic representation
 $\Pi _5$
of
$\Pi _5$
of
 ${\mathrm{GL}}_5({\mathbb A})$
. In particular, if
${\mathrm{GL}}_5({\mathbb A})$
. In particular, if
 $\sigma $
is any irreducible automorphic representation of
$\sigma $
is any irreducible automorphic representation of
 ${\mathrm{GL}}_n({\mathbb A})$
, then we have an equality of degree
${\mathrm{GL}}_n({\mathbb A})$
, then we have an equality of degree
 $5n$
Rankin–Selberg L-functions
$5n$
Rankin–Selberg L-functions
 $L(s, \mathrm {std}(\pi ) \times \sigma )= L(s, \Pi _5 \times \sigma )$
, and therefore
$L(s, \mathrm {std}(\pi ) \times \sigma )= L(s, \Pi _5 \times \sigma )$
, and therefore
 $L(s, \mathrm {std}(\pi ) \times \sigma )$
satisfies the usual properties of an L-function. If
$L(s, \mathrm {std}(\pi ) \times \sigma )$
satisfies the usual properties of an L-function. If
 $n \le 2$
, and
$n \le 2$
, and
 $\sigma $
has the property that the set of finite primes where it is ramified either is empty or contains at least one prime not dividing N, then
$\sigma $
has the property that the set of finite primes where it is ramified either is empty or contains at least one prime not dividing N, then
 $L(s, \mathrm {std}(\pi ) \times \sigma )$
is entire.
$L(s, \mathrm {std}(\pi ) \times \sigma )$
is entire. -
iii) The degree
 $10\ L$
-function
$10\ L$
-function
 $L(s, \mathrm {ad}(\pi ))$
satisfies the usual properties of an L-function, is entire, and has no zeros on the line
$L(s, \mathrm {ad}(\pi ))$
satisfies the usual properties of an L-function, is entire, and has no zeros on the line
 $\mathrm {Re}(s)=1$
.
$\mathrm {Re}(s)=1$
.
Proof. Since F corresponds to the ‘general’ Arthur parameter, Arthur’s work [Reference Andrianov2] (see also [Reference Shahidi59, §1.1]) shows that
![]() $\pi $
has a strong lifting to a cuspidal automorphic representation
$\pi $
has a strong lifting to a cuspidal automorphic representation
![]() $\Pi _4$
of
$\Pi _4$
of
![]() ${\mathrm{GL}}_4$
; clearly
${\mathrm{GL}}_4$
; clearly
![]() $\Pi _4$
has trivial central character, since
$\Pi _4$
has trivial central character, since
![]() $\pi $
does. It is known from [Reference Andrianov2, Theorem 1.5.3] that
$\pi $
does. It is known from [Reference Andrianov2, Theorem 1.5.3] that
![]() $\Pi _4$
is self-dual and symplectic.Footnote
7
The fact that the lifting is ‘strong’ – that is, corresponds to a local lift at all places – implicitly uses the fact that the local Arthur parameters coincide with the local Langlands parameters of Gan and Takeda [Reference Gun, Kohnen and Soundararajan19]; this consistency of local parameters follows from [Reference Chan and Gan10]. The required properties of
$\Pi _4$
is self-dual and symplectic.Footnote
7
The fact that the lifting is ‘strong’ – that is, corresponds to a local lift at all places – implicitly uses the fact that the local Arthur parameters coincide with the local Langlands parameters of Gan and Takeda [Reference Gun, Kohnen and Soundararajan19]; this consistency of local parameters follows from [Reference Chan and Gan10]. The required properties of
![]() $L(s, \pi \times \sigma )$
now follow from the Rankin–Selberg theory of
$L(s, \pi \times \sigma )$
now follow from the Rankin–Selberg theory of
![]() ${\mathrm{GL}}_n$
.
${\mathrm{GL}}_n$
.
For the second assertion, let
![]() $\wedge ^2$
denote the exterior square, and note that
$\wedge ^2$
denote the exterior square, and note that
![]() $\wedge ^2\rho _4=\mathbf {1}+\rho _5$
; hence
$\wedge ^2\rho _4=\mathbf {1}+\rho _5$
; hence
 $$ \begin{align} L\left(s,\Pi_4,\wedge^2\right)=L(s, \mathrm{std}(\pi))\zeta(s). \end{align} $$
$$ \begin{align} L\left(s,\Pi_4,\wedge^2\right)=L(s, \mathrm{std}(\pi))\zeta(s). \end{align} $$
Recall that
 $L(s, \Pi _4 \times \Pi _4) = L\left (s,\Pi _4,\mathrm {Sym}^2\right ) L\left (s,\Pi _4,\wedge ^2\right )$
. Since
$L(s, \Pi _4 \times \Pi _4) = L\left (s,\Pi _4,\mathrm {Sym}^2\right ) L\left (s,\Pi _4,\wedge ^2\right )$
. Since
![]() $\Pi _4$
is symplectic,
$\Pi _4$
is symplectic,
 $L\left (s,\Pi _4,\wedge ^2\right )$
has a simple pole at
$L\left (s,\Pi _4,\wedge ^2\right )$
has a simple pole at
![]() $s=1$
and
$s=1$
and
 $L\left (s,\Pi _4,\mathrm {Sym}^2\right )$
is an entire function by [Reference Borel9, Theorem 7.5]. It follows from equation (54) that
$L\left (s,\Pi _4,\mathrm {Sym}^2\right )$
is an entire function by [Reference Borel9, Theorem 7.5]. It follows from equation (54) that
![]() $L(s, \mathrm {std}(\pi ))$
is holomorphic and nonzero at
$L(s, \mathrm {std}(\pi ))$
is holomorphic and nonzero at
![]() $s=1$
. Together with [Reference Gritsenko20, Theorem 2], we obtain that
$s=1$
. Together with [Reference Gritsenko20, Theorem 2], we obtain that
![]() $L(s, \mathrm {std}(\pi ))$
has no poles on
$L(s, \mathrm {std}(\pi ))$
has no poles on
![]() $\mathrm {Re}(s)=1$
. On the other hand, by [Reference Kohnen32, Theorem A] and [Reference Huang and Lester26],
$\mathrm {Re}(s)=1$
. On the other hand, by [Reference Kohnen32, Theorem A] and [Reference Huang and Lester26],
 $L\left (s,\Pi _4,\wedge ^2\right )$
is the L-function of an automorphic representation of
$L\left (s,\Pi _4,\wedge ^2\right )$
is the L-function of an automorphic representation of
![]() ${\mathrm{GL}}_6({\mathbb A})$
of the form
${\mathrm{GL}}_6({\mathbb A})$
of the form
![]() ${\mathrm{Ind}}(\tau _1\otimes \dotsb \otimes \tau _m) ,$
where
${\mathrm{Ind}}(\tau _1\otimes \dotsb \otimes \tau _m) ,$
where
![]() $\tau _1,\dotsc ,\tau _m$
are unitary, cuspidal, automorphic representations of
$\tau _1,\dotsc ,\tau _m$
are unitary, cuspidal, automorphic representations of
![]() ${\mathrm{GL}}_{n_i}({\mathbb A})$
,
${\mathrm{GL}}_{n_i}({\mathbb A})$
,
![]() $n_1+\dotsb +n_m=6$
. Since
$n_1+\dotsb +n_m=6$
. Since
 $L\left (s,\Pi _4,\wedge ^2\right )$
has a simple pole at
$L\left (s,\Pi _4,\wedge ^2\right )$
has a simple pole at
![]() $s=1$
, it follows that exactly one of the
$s=1$
, it follows that exactly one of the
![]() $\tau _i$
– say
$\tau _i$
– say
![]() $\tau _m$
– is the trivial representation of
$\tau _m$
– is the trivial representation of
![]() ${\mathrm{GL}}_1({\mathbb A})$
. Canceling out one
${\mathrm{GL}}_1({\mathbb A})$
. Canceling out one
![]() $\zeta $
factor, we see that
$\zeta $
factor, we see that
So we take
![]() $\Pi _5={\mathrm{Ind}}(\tau _1\otimes \dotsb \otimes \tau _{m-1}) $
; the foregoing discussion shows that
$\Pi _5={\mathrm{Ind}}(\tau _1\otimes \dotsb \otimes \tau _{m-1}) $
; the foregoing discussion shows that
![]() $\Pi _5$
is a (strong) lifting of
$\Pi _5$
is a (strong) lifting of
![]() $\pi $
from
$\pi $
from
![]() ${\mathrm{GSp}}_4({\mathbb A})$
to
${\mathrm{GSp}}_4({\mathbb A})$
to
![]() ${\mathrm{GL}}_5({\mathbb A})$
with respect to the map
${\mathrm{GL}}_5({\mathbb A})$
with respect to the map
![]() $\rho _5$
of dual groups
$\rho _5$
of dual groups
![]() ${\mathrm{GSp}}_4({\mathbb C}) \rightarrow {\mathrm{SO}}_5({\mathbb C}) \subset {\mathrm{GL}}_5({\mathbb C})$
. Observe that each
${\mathrm{GSp}}_4({\mathbb C}) \rightarrow {\mathrm{SO}}_5({\mathbb C}) \subset {\mathrm{GL}}_5({\mathbb C})$
. Observe that each
![]() $\tau _i$
is unitary, cuspidal, and unramified outside primes dividing N. By Rankin–Selberg theory,
$\tau _i$
is unitary, cuspidal, and unramified outside primes dividing N. By Rankin–Selberg theory,
 $L(s, \Pi _5 \times \sigma )=\prod _{i=1}^{m-1}L(s, \tau _i \times \sigma ) $
satisfies the usual properties of an L-function. To complete the proof, it suffices to show that if
$L(s, \Pi _5 \times \sigma )=\prod _{i=1}^{m-1}L(s, \tau _i \times \sigma ) $
satisfies the usual properties of an L-function. To complete the proof, it suffices to show that if
![]() $\sigma $
is an irreducible cuspidal representation of
$\sigma $
is an irreducible cuspidal representation of
![]() ${\mathrm{GL}}_1({\mathbb A})$
or
${\mathrm{GL}}_1({\mathbb A})$
or
![]() ${\mathrm{GL}}_2({\mathbb A})$
such that the set of ramification primes for
${\mathrm{GL}}_2({\mathbb A})$
such that the set of ramification primes for
![]() $\sigma $
either is empty or contains at least one prime outside N, then
$\sigma $
either is empty or contains at least one prime outside N, then
![]() $\tau _i \not \simeq \hat {\sigma }$
for each i. First, consider the case where
$\tau _i \not \simeq \hat {\sigma }$
for each i. First, consider the case where
![]() $\sigma $
is a character, in which case we are reduced to
$\sigma $
is a character, in which case we are reduced to
![]() $n_i=1$
. In this case, since
$n_i=1$
. In this case, since
![]() $\tau _i$
is unramified outside N, the assumption on
$\tau _i$
is unramified outside N, the assumption on
![]() $\sigma $
means that the situation
$\sigma $
means that the situation
![]() $\tau _i \simeq \hat {\sigma }$
will force
$\tau _i \simeq \hat {\sigma }$
will force
![]() $\tau _i$
to be unramified everywhere, in which case the right-hand side of equation (55) would have a pole on
$\tau _i$
to be unramified everywhere, in which case the right-hand side of equation (55) would have a pole on
![]() $\mathrm {Re}(s)=1$
. This contradicts the observation from before that
$\mathrm {Re}(s)=1$
. This contradicts the observation from before that
![]() $L(s, \mathrm {std}(\pi ))$
has no poles on
$L(s, \mathrm {std}(\pi ))$
has no poles on
![]() $\mathrm {Re}(s)=1$
. Next consider the case where
$\mathrm {Re}(s)=1$
. Next consider the case where
![]() $\sigma $
is a cuspidal representation of
$\sigma $
is a cuspidal representation of
![]() ${\mathrm{GL}}_2({\mathbb A})$
. An identical argument to the foregoing reduces us to the case where
${\mathrm{GL}}_2({\mathbb A})$
. An identical argument to the foregoing reduces us to the case where
![]() $\tau _i \simeq \hat {\sigma }$
is unramified at all finite primes. The easy relation
$\tau _i \simeq \hat {\sigma }$
is unramified at all finite primes. The easy relation
![]() $\wedge ^2\rho _5 = {\mathrm{Sym}}^2\rho _4=\rho _{10}$
implies that
$\wedge ^2\rho _5 = {\mathrm{Sym}}^2\rho _4=\rho _{10}$
implies that
 $$ \begin{align} L\left(s,\Pi_5,\wedge^2\right)= L(s, \mathrm{ad}(\pi)) = L\left(s,\Pi_4,\mathrm{Sym}^2\right), \end{align} $$
$$ \begin{align} L\left(s,\Pi_5,\wedge^2\right)= L(s, \mathrm{ad}(\pi)) = L\left(s,\Pi_4,\mathrm{Sym}^2\right), \end{align} $$
which we know is an entire function. On the other hand, if some
![]() $\tau _i$
in equation (55) has
$\tau _i$
in equation (55) has
![]() $n_i=2$
and is unramified at all finite primes, then
$n_i=2$
and is unramified at all finite primes, then
 $L\left (s,\Pi _5,\wedge ^2\right )$
will contain a factor of
$L\left (s,\Pi _5,\wedge ^2\right )$
will contain a factor of
![]() $L(s, \omega _{\tau _i})$
and so will have a pole on
$L(s, \omega _{\tau _i})$
and so will have a pole on
![]() $\mathrm {Re}(s)=1$
. This contradiction completes the proof that each
$\mathrm {Re}(s)=1$
. This contradiction completes the proof that each
![]() $L(s,\tau _i \times \sigma )$
and hence
$L(s,\tau _i \times \sigma )$
and hence
![]() $L(s,\Pi _5\times \sigma )$
is entire.
$L(s,\Pi _5\times \sigma )$
is entire.
Finally, the assertion concerning the degree
![]() $10\ L$
-function
$10\ L$
-function
![]() $L(s, \mathrm {ad}(\pi ))$
follows from the identity (56) and the fact that
$L(s, \mathrm {ad}(\pi ))$
follows from the identity (56) and the fact that
 $L\left (s,\Pi _4,\mathrm {Sym}^2\right )$
represents a holomorphic L-function. Since symmetric square L-functions are accessible via the Langlands–Shahidi method, the nonvanishing on
$L\left (s,\Pi _4,\mathrm {Sym}^2\right )$
represents a holomorphic L-function. Since symmetric square L-functions are accessible via the Langlands–Shahidi method, the nonvanishing on
![]() $\mathrm {Re}(s)=1$
follows (see [Reference Shahidi60, §5] and [Reference Shimura61, Theorem 1.1]).
$\mathrm {Re}(s)=1$
follows (see [Reference Shahidi60, §5] and [Reference Shimura61, Theorem 1.1]).
For our future applications, we will also need the facts that
![]() $L(s, \mathrm {ad}(\pi ) \times \sigma )$
has the properties of an L-function and is entire for certain special automorphic representations
$L(s, \mathrm {ad}(\pi ) \times \sigma )$
has the properties of an L-function and is entire for certain special automorphic representations
![]() $\sigma $
of
$\sigma $
of
![]() ${\mathrm{GL}}_1({\mathbb A})$
or
${\mathrm{GL}}_1({\mathbb A})$
or
![]() ${\mathrm{GL}}_2({\mathbb A})$
. The next two lemmas achieve this for
${\mathrm{GL}}_2({\mathbb A})$
. The next two lemmas achieve this for
![]() $\sigma $
a quadratic character or
$\sigma $
a quadratic character or
![]() $\sigma $
of the form
$\sigma $
of the form
 ${\mathcal {AI}}\left (\Lambda ^2\right )$
, where
${\mathcal {AI}}\left (\Lambda ^2\right )$
, where
![]() $\Lambda $
is a character of
$\Lambda $
is a character of
![]() ${\mathbb A}_K^\times $
, K is a quadratic field, and
${\mathbb A}_K^\times $
, K is a quadratic field, and
![]() ${\mathcal {AI}}$
denotes automorphic induction.
${\mathcal {AI}}$
denotes automorphic induction.
Lemma 5.5. Let
![]() $K/{\mathbb Q}$
be a quadratic field. Let F and
$K/{\mathbb Q}$
be a quadratic field. Let F and
![]() $\pi $
be as in Proposition 5.4 and assume that N is square-free. Then the base change
$\pi $
be as in Proposition 5.4 and assume that N is square-free. Then the base change
![]() $\pi _K$
of
$\pi _K$
of
![]() $\pi $
to
$\pi $
to
![]() ${\mathrm{GSp}}_4({\mathbb A}_K)$
is cuspidal. Furthermore, the base change
${\mathrm{GSp}}_4({\mathbb A}_K)$
is cuspidal. Furthermore, the base change
![]() $\Pi _{4,K}$
of
$\Pi _{4,K}$
of
![]() $\Pi _4$
to
$\Pi _4$
to
![]() ${\mathrm{GL}}_4({\mathbb A}_K)$
is cuspidal and
${\mathrm{GL}}_4({\mathbb A}_K)$
is cuspidal and
![]() $\Pi _{4,K}$
is the lifting of
$\Pi _{4,K}$
is the lifting of
![]() $\pi _K$
from
$\pi _K$
from
![]() ${\mathrm{GSp}}_4({\mathbb A}_K)$
to
${\mathrm{GSp}}_4({\mathbb A}_K)$
to
![]() ${\mathrm{GL}}_4({\mathbb A}_K)$
.
${\mathrm{GL}}_4({\mathbb A}_K)$
.
Proof. Let
![]() $\pi _K$
and
$\pi _K$
and
![]() $\Pi _{4,K}$
be as in the statement of the lemma. Since
$\Pi _{4,K}$
be as in the statement of the lemma. Since
![]() $\Pi _4$
is the lifting of
$\Pi _4$
is the lifting of
![]() $\pi $
, it follows from the definition of base change that
$\pi $
, it follows from the definition of base change that
![]() $\Pi _{4,K}$
is the lifting of
$\Pi _{4,K}$
is the lifting of
![]() $\pi _K$
. Let
$\pi _K$
. Let
![]() $\sigma $
be an arbitrary cuspidal automorphic representation of
$\sigma $
be an arbitrary cuspidal automorphic representation of
![]() ${\mathrm{GL}}_1({\mathbb A}_K)$
or
${\mathrm{GL}}_1({\mathbb A}_K)$
or
![]() ${\mathrm{GL}}_2({\mathbb A}_K)$
. By the definition of lifting, we have
${\mathrm{GL}}_2({\mathbb A}_K)$
. By the definition of lifting, we have
and so to prove that
![]() $\pi _K$
and
$\pi _K$
and
![]() $\Pi _{4,K}$
are cuspidal it suffices to show that
$\Pi _{4,K}$
are cuspidal it suffices to show that
![]() $L(s, \Pi _{4,K} \times \sigma )$
has no poles. By the adjointness formula [Reference Pitale, Saha and Schmidt48, Proposition 3.1], we have
$L(s, \Pi _{4,K} \times \sigma )$
has no poles. By the adjointness formula [Reference Pitale, Saha and Schmidt48, Proposition 3.1], we have
![]() $L\left (s, \Pi _{4,K} \times \sigma \right ) = L(s, \Pi _4 \times {\mathcal {AI}}(\sigma ))$
. Note that
$L\left (s, \Pi _{4,K} \times \sigma \right ) = L(s, \Pi _4 \times {\mathcal {AI}}(\sigma ))$
. Note that
![]() ${\mathcal {AI}}(\sigma )$
is an automorphic representation of
${\mathcal {AI}}(\sigma )$
is an automorphic representation of
![]() ${\mathrm{GL}}_2({\mathbb A})$
if
${\mathrm{GL}}_2({\mathbb A})$
if
![]() $\sigma $
is a character of
$\sigma $
is a character of
![]() ${\mathbb A}_K^\times $
, and
${\mathbb A}_K^\times $
, and
![]() ${\mathcal {AI}}(\sigma )$
is an automorphic representation of
${\mathcal {AI}}(\sigma )$
is an automorphic representation of
![]() ${\mathrm{GL}}_4({\mathbb A})$
if
${\mathrm{GL}}_4({\mathbb A})$
if
![]() $\sigma $
is a cuspidal representation of
$\sigma $
is a cuspidal representation of
![]() ${\mathrm{GL}}_2({\mathbb A}_K)$
. By Proposition 5.4,
${\mathrm{GL}}_2({\mathbb A}_K)$
. By Proposition 5.4,
![]() $L(s, \Pi _4 \times {\mathcal {AI}}(\sigma ))$
is entire when
$L(s, \Pi _4 \times {\mathcal {AI}}(\sigma ))$
is entire when
![]() $\sigma $
is a character. This reduces us to the case where
$\sigma $
is a character. This reduces us to the case where
![]() $\sigma $
is a cuspidal representation of
$\sigma $
is a cuspidal representation of
![]() ${\mathrm{GL}}_2({\mathbb A}_K)$
; in this case,
${\mathrm{GL}}_2({\mathbb A}_K)$
; in this case,
![]() $L\left (s, \Pi _{4,K} \times \sigma \right ) = L(s, \Pi _4 \times {\mathcal {AI}}(\sigma ))$
has a pole if and only if
$L\left (s, \Pi _{4,K} \times \sigma \right ) = L(s, \Pi _4 \times {\mathcal {AI}}(\sigma ))$
has a pole if and only if
![]() $\Pi _4 \simeq {\mathcal {AI}}(\sigma )$
(recall that
$\Pi _4 \simeq {\mathcal {AI}}(\sigma )$
(recall that
![]() $\Pi _4$
is self-dual). However, by looking at a prime p which ramifies in K, we see that this is impossible: at any such prime, the local Langlands parameter of
$\Pi _4$
is self-dual). However, by looking at a prime p which ramifies in K, we see that this is impossible: at any such prime, the local Langlands parameter of
![]() $\Pi _{4,p}$
is the local lifting of a representation of
$\Pi _{4,p}$
is the local lifting of a representation of
![]() ${\mathrm{GSp}}_4\left ({\mathbb Q}_p\right )$
that has a vector fixed by the local Siegel congruence subgroup of level p (since N is square-free), but an inspection of [Reference Andrianov2
Reference Borel9, Table 1] tells us that the local parameter of
${\mathrm{GSp}}_4\left ({\mathbb Q}_p\right )$
that has a vector fixed by the local Siegel congruence subgroup of level p (since N is square-free), but an inspection of [Reference Andrianov2
Reference Borel9, Table 1] tells us that the local parameter of
![]() ${\mathcal {AI}}\left (\sigma _p\right )$
can never equal one of those. Hence we have completed the proof that
${\mathcal {AI}}\left (\sigma _p\right )$
can never equal one of those. Hence we have completed the proof that
![]() $L\left (s, \Pi _{4,K} \times \sigma \right )$
has no poles.
$L\left (s, \Pi _{4,K} \times \sigma \right )$
has no poles.
Remark 5.6. This proof crucially relies on the fact that F has square-free level N. If N is allowed to be divisible by squares of primes, there indeed exists F whose adelization generates a representation
![]() $\pi $
whose base change
$\pi $
whose base change
![]() $\pi _K$
(for certain K) is noncuspidal. Such F are constructed in [Reference Johnson-Leung and Roberts29] for K real quadratic and in [Reference Blomer and Brumley4] for K imaginary quadratic.
$\pi _K$
(for certain K) is noncuspidal. Such F are constructed in [Reference Johnson-Leung and Roberts29] for K real quadratic and in [Reference Blomer and Brumley4] for K imaginary quadratic.
Lemma 5.7. Let
![]() $K/\mathbb Q$
be a quadratic field. Let F and
$K/\mathbb Q$
be a quadratic field. Let F and
![]() $\pi $
be as in Proposition 5.4 and assume that N is square-free. Let
$\pi $
be as in Proposition 5.4 and assume that N is square-free. Let
![]() $\chi _K$
be the quadratic Dirichlet character associated to the extension
$\chi _K$
be the quadratic Dirichlet character associated to the extension
![]() $K/{\mathbb Q}$
. Let
$K/{\mathbb Q}$
. Let
![]() $\Lambda $
be any idele class character of
$\Lambda $
be any idele class character of
![]() $K^\times \backslash A_K^\times $
. Then the degree
$K^\times \backslash A_K^\times $
. Then the degree
![]() $10\ L$
-function
$10\ L$
-function
![]() $L(s, \mathrm {ad}(\pi )\times \chi _K)$
and the degree
$L(s, \mathrm {ad}(\pi )\times \chi _K)$
and the degree
![]() $20\ L$
-function
$20\ L$
-function
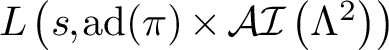 $L\left (s, \mathrm {ad}(\pi )\times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
both satisfy the usual properties of an L-function, and are both entire.
$L\left (s, \mathrm {ad}(\pi )\times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
both satisfy the usual properties of an L-function, and are both entire.
Proof. It can be verified (as a formal identity that holds at each place) that
 $$ \begin{align*} L\left(s, \mathrm{Sym}^2\left(\pi_{4,K} \times \Lambda\right)\right) = L\left(s, \mathrm{ad}(\pi) \times {\mathcal{AI}}\left(\Lambda^2\right)\right). \end{align*} $$
$$ \begin{align*} L\left(s, \mathrm{Sym}^2\left(\pi_{4,K} \times \Lambda\right)\right) = L\left(s, \mathrm{ad}(\pi) \times {\mathcal{AI}}\left(\Lambda^2\right)\right). \end{align*} $$
By Lemma 5.5,
![]() $\pi _{4,K} \times \Lambda $
is a cuspidal representation of
$\pi _{4,K} \times \Lambda $
is a cuspidal representation of
![]() ${\mathrm{GL}}_4({\mathbb A}_K)$
. Furthermore, if
${\mathrm{GL}}_4({\mathbb A}_K)$
. Furthermore, if
![]() $\pi _{4,K} \times \Lambda $
is self-dual, then it must be symplectic, since
$\pi _{4,K} \times \Lambda $
is self-dual, then it must be symplectic, since
![]() $\Pi _{4,K}\times \Lambda $
is the lift of
$\Pi _{4,K}\times \Lambda $
is the lift of
![]() $\pi _K\times \Lambda $
from
$\pi _K\times \Lambda $
from
![]() ${\mathrm{GSp}}_4({\mathbb A}_K)$
to
${\mathrm{GSp}}_4({\mathbb A}_K)$
to
![]() ${\mathrm{GL}}_4({\mathbb A}_K)$
. So by [Reference Borel9, Theorem 7.5],
${\mathrm{GL}}_4({\mathbb A}_K)$
. So by [Reference Borel9, Theorem 7.5],
 $ L\left (s, \mathrm {ad}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
has the properties of an L-function and is entire.
$ L\left (s, \mathrm {ad}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
has the properties of an L-function and is entire.
To show the same fact for
 $L(s, \mathrm {ad}(\pi )\times \chi _K) = L\left (s, \mathrm {Sym}^2(\Pi _4)\times \chi _K\right )$
, we appeal to [Reference Takeda66, Theorem, p. 104], which shows that the only possible poles of
$L(s, \mathrm {ad}(\pi )\times \chi _K) = L\left (s, \mathrm {Sym}^2(\Pi _4)\times \chi _K\right )$
, we appeal to [Reference Takeda66, Theorem, p. 104], which shows that the only possible poles of
 $L\left (s, \mathrm {Sym}^2(\Pi _4)\times \chi _K\right )$
are at
$L\left (s, \mathrm {Sym}^2(\Pi _4)\times \chi _K\right )$
are at
![]() $s=0, 1$
(these two possible poles are related by the functional equation). However, by what we have already proved,
$s=0, 1$
(these two possible poles are related by the functional equation). However, by what we have already proved,
![]() $L(s,\mathrm {ad}(\pi )\times {\mathcal {AI}}(1)) =L( s, \mathrm {ad}(\pi ))L(s, \mathrm {ad}(\pi )\times \chi _K)$
is entire. So a pole at
$L(s,\mathrm {ad}(\pi )\times {\mathcal {AI}}(1)) =L( s, \mathrm {ad}(\pi ))L(s, \mathrm {ad}(\pi )\times \chi _K)$
is entire. So a pole at
![]() $s=1$
for
$s=1$
for
![]() $L(s, \mathrm {ad}(\pi )\times \chi _K)$
would imply that
$L(s, \mathrm {ad}(\pi )\times \chi _K)$
would imply that
![]() $L(1, \mathrm {ad}(\pi ))=0$
. This contradicts the last part of Proposition 5.4.
$L(1, \mathrm {ad}(\pi ))=0$
. This contradicts the last part of Proposition 5.4.
Remark 5.8. Let
 $F \in S_k(\Gamma ^{(2)}_0(N))^{ \rm G}$
give rise to an irreducible representation
$F \in S_k(\Gamma ^{(2)}_0(N))^{ \rm G}$
give rise to an irreducible representation
![]() $\pi $
and assume that N is square-free. Let d be a fundamental discriminant that is divisible by at least one prime not dividing N, put
$\pi $
and assume that N is square-free. Let d be a fundamental discriminant that is divisible by at least one prime not dividing N, put
![]() $K={\mathbb Q}(\sqrt {d})$
, let
$K={\mathbb Q}(\sqrt {d})$
, let
![]() $\chi _d$
be the quadratic Dirichlet character associated to
$\chi _d$
be the quadratic Dirichlet character associated to
![]() $K/{\mathbb Q}$
, and let
$K/{\mathbb Q}$
, and let
![]() $\Lambda $
be a character of the ideal class group
$\Lambda $
be a character of the ideal class group
![]() $\operatorname {\mathrm {Cl}}_K$
. Then combining Proposition 5.4 and Lemma 5.7, we see that the L-functions
$\operatorname {\mathrm {Cl}}_K$
. Then combining Proposition 5.4 and Lemma 5.7, we see that the L-functions
![]() $L(s, \pi \times {\mathcal {AI}}(\Lambda ))$
,
$L(s, \pi \times {\mathcal {AI}}(\Lambda ))$
,
 $L\left (s, \mathrm {ad}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
,
$L\left (s, \mathrm {ad}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
,
![]() $L(s, \mathrm {ad}(\pi ) \times \chi _d)$
,
$L(s, \mathrm {ad}(\pi ) \times \chi _d)$
,
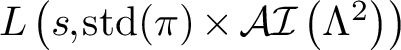 $L\left (s, \mathrm {std}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
, and
$L\left (s, \mathrm {std}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
, and
![]() $L(s, \mathrm {std}(\pi ) \times \chi _d)$
are all holomorphic everywhere in the complex plane.
$L(s, \mathrm {std}(\pi ) \times \chi _d)$
are all holomorphic everywhere in the complex plane.
5.5. A consequence of the refined Gan–Gross–Prasad identity
Let
![]() $K = {\mathbb Q}(\sqrt {d})$
, where
$K = {\mathbb Q}(\sqrt {d})$
, where
![]() $d<0$
is a fundamental discriminant. Recall from the introduction that for any character
$d<0$
is a fundamental discriminant. Recall from the introduction that for any character
![]() $\Lambda $
of the finite group
$\Lambda $
of the finite group
![]() $\operatorname {\mathrm {Cl}}_K$
, we define
$\operatorname {\mathrm {Cl}}_K$
, we define
![]() $B(F, \Lambda ) = \sum _{S \in \operatorname {\mathrm {Cl}}_K}a(F, S) \Lambda (S)$
. The refined Gan–Gross–Prasad conjecture in the context of Bessel periods of
$B(F, \Lambda ) = \sum _{S \in \operatorname {\mathrm {Cl}}_K}a(F, S) \Lambda (S)$
. The refined Gan–Gross–Prasad conjecture in the context of Bessel periods of
![]() ${\mathrm{PGSp}}_4 \simeq {\mathrm{SO}}_5$
(and more generally, for Bessel periods of orthogonal groups) was formulated in [Reference Lester and Radziwiłł40, equation (1.1)] and made more explicit in the context of Siegel cusp forms in [Reference Dickson, Pitale, Saha and Schmidt15]. This conjecture implies an identity expressing the square of
${\mathrm{PGSp}}_4 \simeq {\mathrm{SO}}_5$
(and more generally, for Bessel periods of orthogonal groups) was formulated in [Reference Lester and Radziwiłł40, equation (1.1)] and made more explicit in the context of Siegel cusp forms in [Reference Dickson, Pitale, Saha and Schmidt15]. This conjecture implies an identity expressing the square of
![]() $\lvert B(F, \Lambda )\rvert $
as a ratio of L-values, up to some local integrals. For the purpose of this paper, we only need a relatively weak consequence of this identity, which we formulate explicitly as Hypothesis G. In this subsection we do not assume that N is square-free.
$\lvert B(F, \Lambda )\rvert $
as a ratio of L-values, up to some local integrals. For the purpose of this paper, we only need a relatively weak consequence of this identity, which we formulate explicitly as Hypothesis G. In this subsection we do not assume that N is square-free.
Suppose that
 $F \in S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
gives rise to an irreducible representation
$F \in S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
gives rise to an irreducible representation
![]() $\pi $
. Then F is said to satisfy Hypothesis G if there exists a constant
$\pi $
. Then F is said to satisfy Hypothesis G if there exists a constant
![]() $C_F$
such that for each imaginary quadratic field
$C_F$
such that for each imaginary quadratic field
![]() $K={\mathbb Q}(\sqrt {d})$
(with
$K={\mathbb Q}(\sqrt {d})$
(with
![]() $d<0$
a fundamental discriminant) and each character
$d<0$
a fundamental discriminant) and each character
![]() $\Lambda $
of
$\Lambda $
of
![]() $\operatorname {\mathrm {Cl}}_K$
, we have
$\operatorname {\mathrm {Cl}}_K$
, we have
 $$ \begin{align} \lvert B(F, \Lambda)\rvert^2 \le C_F \lvert d\rvert^{k-1} L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right). \end{align} $$
$$ \begin{align} \lvert B(F, \Lambda)\rvert^2 \le C_F \lvert d\rvert^{k-1} L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right). \end{align} $$
Proposition 5.9. Let
![]() $\pi $
be an irreducible representation that arises from
$\pi $
be an irreducible representation that arises from
 $S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
. Suppose that for each factorizable
$S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
. Suppose that for each factorizable
 $F \in S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
that gives rise to
$F \in S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
that gives rise to
![]() $\pi $
, and each ideal class character
$\pi $
, and each ideal class character
![]() $\Lambda $
of an imaginary quadratic field
$\Lambda $
of an imaginary quadratic field
![]() $K={\mathbb Q}(\sqrt {d})$
(with d a fundamental discriminant), the refined Gan–Gross–Prasad identity (in the form written down in [Reference Dickson, Pitale, Saha and Schmidt15, Conjecture 1.3]) holds for
$K={\mathbb Q}(\sqrt {d})$
(with d a fundamental discriminant), the refined Gan–Gross–Prasad identity (in the form written down in [Reference Dickson, Pitale, Saha and Schmidt15, Conjecture 1.3]) holds for
![]() $(\phi , \Lambda )$
, where
$(\phi , \Lambda )$
, where
![]() $\phi $
is the adelization of F. Then any
$\phi $
is the adelization of F. Then any
 $F \in S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
that gives rise to
$F \in S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
that gives rise to
![]() $\pi $
satisfies Hypothesis G.
$\pi $
satisfies Hypothesis G.
Proof. Note that the subspace of
 $S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
generated by forms that give rise to a fixed irreducible representation
$S_k(\Gamma ^{(2)}_0(N))^{ \rm T}$
generated by forms that give rise to a fixed irreducible representation
![]() $\pi $
has a basis consisting of factorizable forms. So for the purpose of verifying Hypothesis G, it suffices to prove the bound (57) for factorizable F whose adelization
$\pi $
has a basis consisting of factorizable forms. So for the purpose of verifying Hypothesis G, it suffices to prove the bound (57) for factorizable F whose adelization
![]() $\phi = \otimes \phi _v$
generates
$\phi = \otimes \phi _v$
generates
![]() $\pi $
. Assuming the truth of [Reference Dickson, Pitale, Saha and Schmidt15, Conjecture 1.2] for
$\pi $
. Assuming the truth of [Reference Dickson, Pitale, Saha and Schmidt15, Conjecture 1.2] for
![]() $(\phi , \Lambda )$
, and combining it with the explicit calculations performed in [Reference Dickson, Pitale, Saha and Schmidt15, §2.2, §§3.3–3.5], we see that
$(\phi , \Lambda )$
, and combining it with the explicit calculations performed in [Reference Dickson, Pitale, Saha and Schmidt15, §2.2, §§3.3–3.5], we see that
 $$ \begin{align*} \vert B(F, \Lambda)\rvert^2 = A_F \lvert d\rvert^{k-1} L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right) \prod_{p\mid N_F}J_p\left(\phi_p, \Lambda_p\right), \end{align*} $$
$$ \begin{align*} \vert B(F, \Lambda)\rvert^2 = A_F \lvert d\rvert^{k-1} L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right) \prod_{p\mid N_F}J_p\left(\phi_p, \Lambda_p\right), \end{align*} $$
where
![]() $A_F$
depends on F,
$A_F$
depends on F,
![]() $N_F\mid N$
is the smallest integer such that
$N_F\mid N$
is the smallest integer such that
 $F \in S_k(\Gamma ^{(2)}_0(N_F))^{\mathrm{T}}$
, and the normalized local factors
$F \in S_k(\Gamma ^{(2)}_0(N_F))^{\mathrm{T}}$
, and the normalized local factors
![]() $J_p\left (\phi _p, \Lambda _p\right )$
(which depend on p,
$J_p\left (\phi _p, \Lambda _p\right )$
(which depend on p,
![]() $\phi _p$
,
$\phi _p$
,
![]() $\Lambda _p$
, and d) are defined in [Reference Dickson, Pitale, Saha and Schmidt15, equation (30)]. To complete the proof, it suffices to show that
$\Lambda _p$
, and d) are defined in [Reference Dickson, Pitale, Saha and Schmidt15, equation (30)]. To complete the proof, it suffices to show that
![]() $J_p\left (\phi _p, \Lambda _p\right ) \ll _{p,\phi _p} 1$
(i.e., is bounded by some constant that depends on p and
$J_p\left (\phi _p, \Lambda _p\right ) \ll _{p,\phi _p} 1$
(i.e., is bounded by some constant that depends on p and
![]() $\phi _p$
but not on d or
$\phi _p$
but not on d or
![]() $\Lambda _p$
). It suffices to show this for the unnormalized local factors
$\Lambda _p$
). It suffices to show this for the unnormalized local factors
![]() $J_{0,p}\left (\phi _p, \Lambda _p\right )$
defined in [Reference Dickson, Pitale, Saha and Schmidt15, equation (29)], since the normalized local L-factors
$J_{0,p}\left (\phi _p, \Lambda _p\right )$
defined in [Reference Dickson, Pitale, Saha and Schmidt15, equation (29)], since the normalized local L-factors
![]() $J_p\left (\phi _p, \Lambda _p\right )$
differ from these only by certain absolutely bounded L-factors appearing in [Reference Dickson, Pitale, Saha and Schmidt15, equation (30)].
$J_p\left (\phi _p, \Lambda _p\right )$
differ from these only by certain absolutely bounded L-factors appearing in [Reference Dickson, Pitale, Saha and Schmidt15, equation (30)].
To show this, we move to a purely local setup. Let p be a prime dividing
![]() $N_F$
. Let
$N_F$
. Let
![]() $F ={\mathbb Q}_p$
. We fix a set M of coset representatives of
$F ={\mathbb Q}_p$
. We fix a set M of coset representatives of
![]() $F^\times / (F^\times )^2$
such that all elements of M are taken from
$F^\times / (F^\times )^2$
such that all elements of M are taken from
![]() ${\mathbb Z}_p$
, and each
${\mathbb Z}_p$
, and each
![]() $r \in M$
generates the discriminant ideal of
$r \in M$
generates the discriminant ideal of
![]() $F\left (\sqrt {r}\right )/F$
. We let
$F\left (\sqrt {r}\right )/F$
. We let
![]() $r_p$
equal the unique representative in M that corresponds to d. The assumptions imply that
$r_p$
equal the unique representative in M that corresponds to d. The assumptions imply that
 $$ \begin{align*} r_p = d u_p^2, \qquad \text{for some }u \in \left({\mathbb Z}_p^\times\right)^2. \end{align*} $$
$$ \begin{align*} r_p = d u_p^2, \qquad \text{for some }u \in \left({\mathbb Z}_p^\times\right)^2. \end{align*} $$
Let K equal
![]() $F\times F$
(the ‘split case’) if
$F\times F$
(the ‘split case’) if
![]() $r_p \in F^2$
and
$r_p \in F^2$
and
 $K=F\left (\sqrt {r_p}\right )= F(\sqrt {d})$
(the ‘field case’) if
$K=F\left (\sqrt {r_p}\right )= F(\sqrt {d})$
(the ‘field case’) if
![]() $r_p \notin F^2$
. Fix the matrix
$r_p \notin F^2$
. Fix the matrix
![]() $S=S_d$
as in [Reference Dickson, Pitale, Saha and Schmidt15, (75)], so that
$S=S_d$
as in [Reference Dickson, Pitale, Saha and Schmidt15, (75)], so that
![]() $S_d$
has discriminant d. Let
$S_d$
has discriminant d. Let
![]() $T(F)=T_S(F) \simeq K^\times $
be the associated subgroup of
$T(F)=T_S(F) \simeq K^\times $
be the associated subgroup of
![]() ${\mathrm{GSp}}_4(F)$
and let
${\mathrm{GSp}}_4(F)$
and let
![]() $N(F)\subset {\mathrm{GSp}}_4(F)$
denote the unipotent for the Siegel parabolic and
$N(F)\subset {\mathrm{GSp}}_4(F)$
denote the unipotent for the Siegel parabolic and
![]() $\theta _S$
the character on
$\theta _S$
the character on
![]() $N(F)$
given by
$N(F)$
given by
 $\theta _S\left ({\left (\begin {array}{@{}cc@{}}I_2&X\\0&I_2\end {array}\right )}\right ) = \psi (\mathrm {tr}(SX))$
, where
$\theta _S\left ({\left (\begin {array}{@{}cc@{}}I_2&X\\0&I_2\end {array}\right )}\right ) = \psi (\mathrm {tr}(SX))$
, where
![]() $\psi $
is a fixed unramified additive character. Then we need to show that the integral
$\psi $
is a fixed unramified additive character. Then we need to show that the integral
 $$ \begin{align*} J_{0,p}\left(\phi_p, \Lambda_p\right) =\int_{F^\times \backslash T(F)}\int^{{\textrm{St}}}_{N(F)}\left\langle \pi_p\left(t_pn_p\right) \phi_p , \phi_p \right\rangle \Lambda_p^{-1}\left(t_p\right) \theta_S^{-1}\left(n_p\right)dn_p dt_p \end{align*} $$
$$ \begin{align*} J_{0,p}\left(\phi_p, \Lambda_p\right) =\int_{F^\times \backslash T(F)}\int^{{\textrm{St}}}_{N(F)}\left\langle \pi_p\left(t_pn_p\right) \phi_p , \phi_p \right\rangle \Lambda_p^{-1}\left(t_p\right) \theta_S^{-1}\left(n_p\right)dn_p dt_p \end{align*} $$
is bounded by some quantity that does not depend on d or
![]() $\Lambda _p$
. Note that the superscript ‘
$\Lambda _p$
. Note that the superscript ‘
![]() ${\mathrm{St}}$
’ denotes a stable integral as in [Reference Lester and Radziwiłł40]; this means that the integral can be replaced by any sufficiently large compact subgroup (as we will do later). Put
${\mathrm{St}}$
’ denotes a stable integral as in [Reference Lester and Radziwiłł40]; this means that the integral can be replaced by any sufficiently large compact subgroup (as we will do later). Put
 $S'={\left (\begin {array}{@{}cc@{}}-\frac {r_p}4&0\\0&1\end {array}\right )}, A' = {\left (\begin {array}{@{}cc@{}}u_p&0\\0&1\end {array}\right )}$
if
$S'={\left (\begin {array}{@{}cc@{}}-\frac {r_p}4&0\\0&1\end {array}\right )}, A' = {\left (\begin {array}{@{}cc@{}}u_p&0\\0&1\end {array}\right )}$
if
![]() $d \equiv 0 \pmod {4}$
. In the case where
$d \equiv 0 \pmod {4}$
. In the case where
![]() $d \equiv 1 \pmod {4}$
, we put
$d \equiv 1 \pmod {4}$
, we put
 $S' = {\left (\begin {array}{@{}cc@{}}\frac {1-r_p}4&\frac 12\\\frac 12&1\end {array}\right )}, A' = {\left (\begin {array}{@{}cc@{}}u_p&0\\\frac {1-u_p}{2}&1\end {array}\right )}$
. In either case,
$S' = {\left (\begin {array}{@{}cc@{}}\frac {1-r_p}4&\frac 12\\\frac 12&1\end {array}\right )}, A' = {\left (\begin {array}{@{}cc@{}}u_p&0\\\frac {1-u_p}{2}&1\end {array}\right )}$
. In either case,
![]() $A' \in {\mathrm{GL}}_2\left ({\mathbb Z}_p\right )$
and
$A' \in {\mathrm{GL}}_2\left ({\mathbb Z}_p\right )$
and
![]() $S'={}^t\!{A}SA$
. To show that
$S'={}^t\!{A}SA$
. To show that
![]() $J_p$
is bounded independently of d, we use a simple change of variables
$J_p$
is bounded independently of d, we use a simple change of variables
 $\left (n_p \mapsto An_p{}^t\!{A}, \ t_p \mapsto At_p'A^{-1}\right )$
to see that the integral
$\left (n_p \mapsto An_p{}^t\!{A}, \ t_p \mapsto At_p'A^{-1}\right )$
to see that the integral
![]() $J_{0,p}\left (\phi _p, \Lambda _p\right )$
remains unchanged when the matrix S is replaced by
$J_{0,p}\left (\phi _p, \Lambda _p\right )$
remains unchanged when the matrix S is replaced by
![]() $S'$
. This shows that
$S'$
. This shows that
![]() $J_{0,p}\left (\phi _p, \Lambda _p\right )$
depends not on the actual value of d but only on the class of d in
$J_{0,p}\left (\phi _p, \Lambda _p\right )$
depends not on the actual value of d but only on the class of d in
![]() $F^\times / (F^\times )^2$
together with d modulo
$F^\times / (F^\times )^2$
together with d modulo
![]() $4$
, of which there are only finitely many possibilities. To show that the resulting integral is absolutely bounded independently of
$4$
, of which there are only finitely many possibilities. To show that the resulting integral is absolutely bounded independently of
![]() $\Lambda $
, we replace the integral
$\Lambda $
, we replace the integral
 $\int ^{{\mathrm{St}}}_{N(F)}$
by
$\int ^{{\mathrm{St}}}_{N(F)}$
by
 $\int _{p^{-m_p}N\left ({\mathbb Z}_p\right )}$
, where
$\int _{p^{-m_p}N\left ({\mathbb Z}_p\right )}$
, where
![]() $m_p$
depends only on the level N (as follows from the argument of [Reference Dickson, Pitale, Saha and Schmidt15, Proposition 2.14]). The resulting integral is absolutely convergent [Reference Lester and Radziwiłł40, Theorem 2.1(i)] and hence bounded independently of
$m_p$
depends only on the level N (as follows from the argument of [Reference Dickson, Pitale, Saha and Schmidt15, Proposition 2.14]). The resulting integral is absolutely convergent [Reference Lester and Radziwiłł40, Theorem 2.1(i)] and hence bounded independently of
![]() $\Lambda $
.
$\Lambda $
.
Remark 5.10. Furusawa and Morimoto [Reference Furusawa18] have proved the refined Gan–Gross–Prasad identity in the form required in Proposition 5.9 for
![]() $\Lambda =1_K$
, and they have announced a proof of this identity for general
$\Lambda =1_K$
, and they have announced a proof of this identity for general
![]() $\Lambda $
.
$\Lambda $
.
Remark 5.11. Under certain assumptions (namely N odd and square-free, F a newform, and
 $\left ( \frac {d}{p} \right ) = -1$
for all primes p dividing N), the relevant local integrals were explicitly computed in [Reference Dickson, Pitale, Saha and Schmidt15], and so under these assumptions Proposition 5.9 follows from [Reference Dickson, Pitale, Saha and Schmidt15, Theorem 1.13].
$\left ( \frac {d}{p} \right ) = -1$
for all primes p dividing N), the relevant local integrals were explicitly computed in [Reference Dickson, Pitale, Saha and Schmidt15], and so under these assumptions Proposition 5.9 follows from [Reference Dickson, Pitale, Saha and Schmidt15, Theorem 1.13].
Corollary 5.12. Suppose that
 $F \in S_k(\Gamma ^{(2)}_0(N))^{ \rm Y}$
gives rise to an irreducible representation. Then F satisfies Hypothesis G.
$F \in S_k(\Gamma ^{(2)}_0(N))^{ \rm Y}$
gives rise to an irreducible representation. Then F satisfies Hypothesis G.
Proof. This follows from Proposition 5.9, since the refined Gan–Gross–Prasad conjecture is known for Yoshida lifts by [Reference Lester and Radziwiłł40, Theorem 4.3].
Proof of Corollary 1.1. Let
![]() $\pi $
be a cuspidal automorphic representation of
$\pi $
be a cuspidal automorphic representation of
![]() ${\mathrm{GSp}}_4({\mathbb A})$
that arises from a form
${\mathrm{GSp}}_4({\mathbb A})$
that arises from a form
 $F \in S_k(\Gamma _0^{(2)}(N))^{\mathrm{T}}$
with
$F \in S_k(\Gamma _0^{(2)}(N))^{\mathrm{T}}$
with
![]() $k>2$
even and N odd and square-free. Assume that the refined Gan–Gross–Prasad identity holds. Then for any fundamental matrix
$k>2$
even and N odd and square-free. Assume that the refined Gan–Gross–Prasad identity holds. Then for any fundamental matrix
![]() $S \in \Lambda _2$
of discriminant d, we put
$S \in \Lambda _2$
of discriminant d, we put
![]() $K={\mathbb Q}(\sqrt {d})$
and use Cauchy–Schwarz and Proposition 5.9 to conclude
$K={\mathbb Q}(\sqrt {d})$
and use Cauchy–Schwarz and Proposition 5.9 to conclude
 $$ \begin{align*} \lvert a(F,S)\rvert^2 &= \frac{1}{\lvert \operatorname{\mathrm{Cl}}_K\rvert^2}\left\lvert\sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} B(F, \Lambda) \Lambda^{-1}(S)\right\rvert^2 \le \frac{1}{\lvert\operatorname{\mathrm{Cl}}_K\rvert}\sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} \lvert B(F, \Lambda)\rvert^2 \\ &\ll_{\pi} \lvert d\rvert^{k-1}\frac{1}{\lvert\operatorname{\mathrm{Cl}}_K\rvert}\sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right). \end{align*} $$
$$ \begin{align*} \lvert a(F,S)\rvert^2 &= \frac{1}{\lvert \operatorname{\mathrm{Cl}}_K\rvert^2}\left\lvert\sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} B(F, \Lambda) \Lambda^{-1}(S)\right\rvert^2 \le \frac{1}{\lvert\operatorname{\mathrm{Cl}}_K\rvert}\sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} \lvert B(F, \Lambda)\rvert^2 \\ &\ll_{\pi} \lvert d\rvert^{k-1}\frac{1}{\lvert\operatorname{\mathrm{Cl}}_K\rvert}\sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right). \end{align*} $$
The proof of the corollary now follows from Theorem B.□
Proof of Corollary 1.2. For
![]() $f, g$
as in Corollary 1.2 and
$f, g$
as in Corollary 1.2 and
![]() $N=\mathrm {lcm}(N_1, N_2)$
, there exists
$N=\mathrm {lcm}(N_1, N_2)$
, there exists
 $F \in S_k(\Gamma _0^{(2)}(N))^{\mathrm{{Y}}}$
which gives rise to an irreducible representation
$F \in S_k(\Gamma _0^{(2)}(N))^{\mathrm{{Y}}}$
which gives rise to an irreducible representation
![]() $\pi $
such that (see [Reference Schmidt58, Proposition 3.1])
$\pi $
such that (see [Reference Schmidt58, Proposition 3.1])
Now Corollary 1.2 follows from Corollary 1.1 and the triangle inequality.□
Proposition 5.13. Suppose that
 $F \in S_k(\Gamma ^{(2)}_0(N))^{ \rm CAP}$
gives rise to an irreducible representation
$F \in S_k(\Gamma ^{(2)}_0(N))^{ \rm CAP}$
gives rise to an irreducible representation
![]() $\pi $
such that
$\pi $
such that
 $L^N(s, \pi )= L^N(s, \pi _0)\zeta ^N\left (s+\frac 12\right )\zeta ^N\left (s-\frac 12\right )$
, where
$L^N(s, \pi )= L^N(s, \pi _0)\zeta ^N\left (s+\frac 12\right )\zeta ^N\left (s-\frac 12\right )$
, where
![]() $\pi _0$
is a representation of
$\pi _0$
is a representation of
![]() ${\mathrm{GL}}_2({\mathbb A})$
. Then the Fourier coefficients of F at fundamental matrices depend on only the associated discriminant – that is, if
${\mathrm{GL}}_2({\mathbb A})$
. Then the Fourier coefficients of F at fundamental matrices depend on only the associated discriminant – that is, if
![]() $S_1, S_2$
are two fundamental matrices with the same discriminant d, then
$S_1, S_2$
are two fundamental matrices with the same discriminant d, then
![]() $a(F, S_1) = a(F, S_2)$
. Furthermore, there exists a constant
$a(F, S_1) = a(F, S_2)$
. Furthermore, there exists a constant
![]() $C_F$
such that for each fundamental discriminant d and any matrix S of discriminant d, we have
$C_F$
such that for each fundamental discriminant d and any matrix S of discriminant d, we have
 $$ \begin{align*} \lvert a(F, S)\rvert \le C_F \lvert d\rvert^{\frac{k}{2}-\frac34} L\left(\tfrac12, \pi_0 \times \chi_d\right)^{1/2}. \end{align*} $$
$$ \begin{align*} \lvert a(F, S)\rvert \le C_F \lvert d\rvert^{\frac{k}{2}-\frac34} L\left(\tfrac12, \pi_0 \times \chi_d\right)^{1/2}. \end{align*} $$
Proof. An analogue of the Gan–Gross–Prasad conjecture for representations of Saito–Kurokawa type was formulated and proved by Qiu in [Reference Qiu49]. In particular, we have
![]() $B(F, \Lambda )=0$
unless
$B(F, \Lambda )=0$
unless
![]() $\Lambda $
is the trivial character, which proves the assertion that the Fourier coefficients of F at fundamental matrices depend on only the discriminant. For
$\Lambda $
is the trivial character, which proves the assertion that the Fourier coefficients of F at fundamental matrices depend on only the discriminant. For
![]() $\Lambda $
trivial, the desired inequality follows in a similar fashion as in the proof of Proposition 5.9.
$\Lambda $
trivial, the desired inequality follows in a similar fashion as in the proof of Proposition 5.9.
5.6. Proof of Theorem C
In this subsection we restate and prove Theorem C, assuming the main result of §6.
Theorem 5.14. Let
![]() $k>2$
be even and
$k>2$
be even and
![]() $N\ge 1$
be square-free.
$N\ge 1$
be square-free.
-
i) Assume that the GRH holds for each of the L-functions
 $L(s, \pi \times {\mathcal {AI}}(\Lambda ))$
,
$L(s, \pi \times {\mathcal {AI}}(\Lambda ))$
,
 $L\left (s, \mathrm {ad}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
,
$L\left (s, \mathrm {ad}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
,
 $L(s, \mathrm {ad}(\pi ) \times \chi _d)$
,
$L(s, \mathrm {ad}(\pi ) \times \chi _d)$
,
 $L\left (s, \mathrm {std}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
,
$L\left (s, \mathrm {std}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
,
 $L(s, \mathrm {std}(\pi ) \times \chi _d)$
,
$L(s, \mathrm {std}(\pi ) \times \chi _d)$
,
 $L(s, \sigma \times \chi _d)$
, and
$L(s, \sigma \times \chi _d)$
, and
 $L(s,\chi _d)$
, where
$L(s,\chi _d)$
, where
 $\pi $
is any automorphic representation of
$\pi $
is any automorphic representation of
 ${\mathrm{GSp}}_4({\mathbb A})$
that arises from
${\mathrm{GSp}}_4({\mathbb A})$
that arises from
 $S_k(\Gamma _0^{(2)}(N))^{\mathrm{G}}$
,
$S_k(\Gamma _0^{(2)}(N))^{\mathrm{G}}$
,
 $\sigma $
is any cuspidal automorphic representation of
$\sigma $
is any cuspidal automorphic representation of
 ${\mathrm{GL}}_2({\mathbb A})$
,
${\mathrm{GL}}_2({\mathbb A})$
,
 $K={\mathbb Q}(\sqrt {d})$
is an imaginary quadratic field with associated Dirichlet character
$K={\mathbb Q}(\sqrt {d})$
is an imaginary quadratic field with associated Dirichlet character
 $\chi _d$
, and
$\chi _d$
, and
 $\Lambda $
is an ideal class character of K.
$\Lambda $
is an ideal class character of K. -
ii) Assume that each
 $F' \in S_k(\Gamma ^{(2)}_0(N))^{ \rm G}$
that gives rise to an irreducible representation satisfies Hypothesis G (by Proposition 5.9, this is implied by the refined Gan–Gross–Prasad conjecture).
$F' \in S_k(\Gamma ^{(2)}_0(N))^{ \rm G}$
that gives rise to an irreducible representation satisfies Hypothesis G (by Proposition 5.9, this is implied by the refined Gan–Gross–Prasad conjecture).
Then given any
 $F \in S_k(\Gamma ^{(2)}_0(N))$
, we have, for fundamental matrices S,
$F \in S_k(\Gamma ^{(2)}_0(N))$
, we have, for fundamental matrices S,
 $$ \begin{align} \lvert a(F,S)\rvert \ll_{F, \varepsilon} \frac{\lvert{\mathrm{disc}}(S)\rvert^{\frac{k}2 - \frac{1}{2}}}{ (\log \lvert{\mathrm{disc}}(S)\rvert)^{\frac18 - \varepsilon}}. \end{align} $$
$$ \begin{align} \lvert a(F,S)\rvert \ll_{F, \varepsilon} \frac{\lvert{\mathrm{disc}}(S)\rvert^{\frac{k}2 - \frac{1}{2}}}{ (\log \lvert{\mathrm{disc}}(S)\rvert)^{\frac18 - \varepsilon}}. \end{align} $$
Remark 5.15. Concerning the automorphy of the various representations that appear in the statement of Theorem 5.14, we refer the reader to the statements and proofs of Proposition 5.4 and Lemma 5.7.
Proof. Since
 $S_k(\Gamma ^{(2)}_0(N))$
has a basis consisting of forms that give rise to irreducible representations, it suffices to prove the bound (58) for such forms F. Furthermore, we may assume that
$S_k(\Gamma ^{(2)}_0(N))$
has a basis consisting of forms that give rise to irreducible representations, it suffices to prove the bound (58) for such forms F. Furthermore, we may assume that
![]() $d={\mathrm{disc}}(S)$
is divisible by at least one prime not dividing N, since there are at most finitely many fundamental S without this property. Let F give rise to
$d={\mathrm{disc}}(S)$
is divisible by at least one prime not dividing N, since there are at most finitely many fundamental S without this property. Let F give rise to
![]() $\pi $
. We consider three cases, corresponding to decomposition (53).
$\pi $
. We consider three cases, corresponding to decomposition (53).
Case 1:
![]() $\pi $
is of Saito-Kurokawa type. In this case, using Proposition 5.13, the desired inequality follows from any subconvexity bound for
$\pi $
is of Saito-Kurokawa type. In this case, using Proposition 5.13, the desired inequality follows from any subconvexity bound for
 $L\left (\tfrac 12, \pi _0 \times \chi _d\right )$
, which is known. (In particular, for this case, we do not need to appeal to GRH for
$L\left (\tfrac 12, \pi _0 \times \chi _d\right )$
, which is known. (In particular, for this case, we do not need to appeal to GRH for
![]() $L(s, \pi _0 \times \chi _d)$
).
$L(s, \pi _0 \times \chi _d)$
).
Case 2:
![]() $\pi $
is of Yoshida type – that is,
$\pi $
is of Yoshida type – that is,
 $F \in S_k(\Gamma ^{(2)}_0(N))^{\mathrm{Y}}$
. In this case, there are inequivalent representations
$F \in S_k(\Gamma ^{(2)}_0(N))^{\mathrm{Y}}$
. In this case, there are inequivalent representations
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\sigma _2$
of
$\sigma _2$
of
![]() ${\mathrm{GL}}_2({\mathbb A})$
such that
${\mathrm{GL}}_2({\mathbb A})$
such that
 $L\left (\tfrac 12, \pi \times {\mathcal {AI}}(\Lambda )\right ) = L\left (\tfrac 12, \sigma _1 \times {\mathcal {AI}}(\Lambda )\right ) \ L\left (\tfrac 12, \sigma _2 \times {\mathcal {AI}}(\Lambda )\right ).$
Using the identity
$L\left (\tfrac 12, \pi \times {\mathcal {AI}}(\Lambda )\right ) = L\left (\tfrac 12, \sigma _1 \times {\mathcal {AI}}(\Lambda )\right ) \ L\left (\tfrac 12, \sigma _2 \times {\mathcal {AI}}(\Lambda )\right ).$
Using the identity
 $a(F,S) = \frac {1}{\lvert \operatorname {\mathrm {Cl}}_K\rvert }\sum _{\Lambda \in \widehat {\operatorname {\mathrm {Cl}}_K}} B(F, \Lambda ) \Lambda ^{-1}(S)$
and Corollary 5.12, we conclude that
$a(F,S) = \frac {1}{\lvert \operatorname {\mathrm {Cl}}_K\rvert }\sum _{\Lambda \in \widehat {\operatorname {\mathrm {Cl}}_K}} B(F, \Lambda ) \Lambda ^{-1}(S)$
and Corollary 5.12, we conclude that
 $$ \begin{align*} a(F,S) \ll_F \lvert d\rvert^{\frac{k}{2} - \frac12} \frac{1}{\lvert\operatorname{\mathrm{Cl}}_K\rvert}\sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} \sqrt{L\left(\tfrac12, \sigma_1 \times {\mathcal{AI}}(\Lambda)\right) L\left(\tfrac12, \sigma_2 \times {\mathcal{AI}}(\Lambda)\right)}. \end{align*} $$
$$ \begin{align*} a(F,S) \ll_F \lvert d\rvert^{\frac{k}{2} - \frac12} \frac{1}{\lvert\operatorname{\mathrm{Cl}}_K\rvert}\sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} \sqrt{L\left(\tfrac12, \sigma_1 \times {\mathcal{AI}}(\Lambda)\right) L\left(\tfrac12, \sigma_2 \times {\mathcal{AI}}(\Lambda)\right)}. \end{align*} $$
Now the desired conclusion follows from [Reference Böcherer and Das5, Theorem 3].
Case 3:
![]() $\pi $
is of general type – that is,
$\pi $
is of general type – that is,
 $F \in S_k(\Gamma ^{(2)}_0(N))^{\mathrm{G}}$
. In this case, using
$F \in S_k(\Gamma ^{(2)}_0(N))^{\mathrm{G}}$
. In this case, using
 $a(F,S) = \frac {1}{\lvert \operatorname {\mathrm {Cl}}_K\rvert }\sum _{\Lambda \in \widehat {\operatorname {\mathrm {Cl}}_K}} B(F, \Lambda ) \Lambda ^{-1}(S)$
and Hypothesis G, we get
$a(F,S) = \frac {1}{\lvert \operatorname {\mathrm {Cl}}_K\rvert }\sum _{\Lambda \in \widehat {\operatorname {\mathrm {Cl}}_K}} B(F, \Lambda ) \Lambda ^{-1}(S)$
and Hypothesis G, we get
 $$ \begin{align*} a(F,S) \ll_F \lvert d\rvert^{\frac{k}{2} - \frac12} \frac{1}{\lvert\operatorname{\mathrm{Cl}}_K\rvert}\sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} \sqrt{L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right)}. \end{align*} $$
$$ \begin{align*} a(F,S) \ll_F \lvert d\rvert^{\frac{k}{2} - \frac12} \frac{1}{\lvert\operatorname{\mathrm{Cl}}_K\rvert}\sum_{\Lambda \in \widehat{\operatorname{\mathrm{Cl}}_K}} \sqrt{L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right)}. \end{align*} $$
Now the desired conclusion follows from Theorem 6.1, which will be proved in the next section.
6. Fractional moments of central L-values
6.1. Statement of result
Throughout this section, we let
![]() $\pi $
denote an irreducible cuspidal automorphic representation of
$\pi $
denote an irreducible cuspidal automorphic representation of
![]() ${\mathrm{GSp}}_4({\mathbb A})$
that arises from
${\mathrm{GSp}}_4({\mathbb A})$
that arises from
![]() $S_k(\Gamma _0(N))^{\mathrm{G}}$
(see §5.4). Assume that
$S_k(\Gamma _0(N))^{\mathrm{G}}$
(see §5.4). Assume that
![]() $N\ge 1$
is square-free and
$N\ge 1$
is square-free and
![]() $k \ge 2$
. Let
$k \ge 2$
. Let
![]() $K=\mathbb Q(\sqrt {d})$
be a quadratic field such that
$K=\mathbb Q(\sqrt {d})$
be a quadratic field such that
![]() $d<0$
is a fundamental discriminant divisible by at least one prime not dividing N, and let
$d<0$
is a fundamental discriminant divisible by at least one prime not dividing N, and let
![]() $\operatorname {Cl}_K$
denote the ideal class group of K. Also, given
$\operatorname {Cl}_K$
denote the ideal class group of K. Also, given
![]() $\Lambda \in \widehat { \operatorname {Cl}_K}$
, we let
$\Lambda \in \widehat { \operatorname {Cl}_K}$
, we let
![]() ${\mathcal {AI}}(\Lambda )$
denote the automorphic representation of
${\mathcal {AI}}(\Lambda )$
denote the automorphic representation of
![]() ${\mathrm{GL}}_2({\mathbb A})$
given by automorphic induction; it is generated by the theta series
${\mathrm{GL}}_2({\mathbb A})$
given by automorphic induction; it is generated by the theta series
 $\Theta _{\Lambda }(z) = \sum _{ 0 \neq \mathfrak a \subset \mathcal O_K} \Lambda (\mathfrak a) e(N(\mathfrak a) z) .$
Our assumptions imply that the L-functions
$\Theta _{\Lambda }(z) = \sum _{ 0 \neq \mathfrak a \subset \mathcal O_K} \Lambda (\mathfrak a) e(N(\mathfrak a) z) .$
Our assumptions imply that the L-functions
![]() $L(s, \pi \times {\mathcal {AI}}(\Lambda ))$
,
$L(s, \pi \times {\mathcal {AI}}(\Lambda ))$
,
 $L\left (s, \mathrm {ad}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
,
$L\left (s, \mathrm {ad}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
,
![]() $L(s, \mathrm {ad}(\pi ) \times \chi _d)$
,
$L(s, \mathrm {ad}(\pi ) \times \chi _d)$
,
 $L\left (s, \mathrm {std}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
, and
$L\left (s, \mathrm {std}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
, and
![]() $L(s, \mathrm {std}(\pi ) \times \chi _d)$
are all entire (see Remark 5.8). Using Soundararajan’s method [Reference Saha and Schmidt64] for bounding moments of L-functions, we will prove the following result:
$L(s, \mathrm {std}(\pi ) \times \chi _d)$
are all entire (see Remark 5.8). Using Soundararajan’s method [Reference Saha and Schmidt64] for bounding moments of L-functions, we will prove the following result:
Theorem 6.1. Assume the GRH for each of the L-functions
![]() $L(s, \pi \times {\mathcal {AI}}(\Lambda ))$
,
$L(s, \pi \times {\mathcal {AI}}(\Lambda ))$
,
 $L\left (s, \mathrm {ad}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
,
$L\left (s, \mathrm {ad}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
,
![]() $L(s, \mathrm {ad}(\pi ) \times \chi _d)$
,
$L(s, \mathrm {ad}(\pi ) \times \chi _d)$
,
 $L\left (s, \mathrm {std}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
,
$L\left (s, \mathrm {std}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
,
![]() $L(s, \mathrm {std}(\pi ) \times \chi _d)$
, and
$L(s, \mathrm {std}(\pi ) \times \chi _d)$
, and
![]() $L(s,\chi _d)$
. Then
$L(s,\chi _d)$
. Then
 $$ \begin{align*} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{ \operatorname{Cl}_K}} \sqrt{ L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right)} \ll_{\pi,\varepsilon} \frac{1}{(\log \lvert d\rvert)^{\frac18-\varepsilon}}. \end{align*} $$
$$ \begin{align*} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{ \operatorname{Cl}_K}} \sqrt{ L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right)} \ll_{\pi,\varepsilon} \frac{1}{(\log \lvert d\rvert)^{\frac18-\varepsilon}}. \end{align*} $$
Related moment estimates for families of L-functions have been established in [Reference Böcherer and Das5, Reference He and Zhao27, Reference Liu38, Reference Blomer and Brumley4
Reference Arthur3]. Since we assume the GRH, we immediately get that
 $L\left (\tfrac 12, \pi \times {\mathcal {AI}}(\Lambda )\right ) \ge 0$
, which incidentally also follows from the refined Gan–Gross–Prasad identity using formula (57). However, the nonnegativity of
$L\left (\tfrac 12, \pi \times {\mathcal {AI}}(\Lambda )\right ) \ge 0$
, which incidentally also follows from the refined Gan–Gross–Prasad identity using formula (57). However, the nonnegativity of
 $L\left (\tfrac 12, \pi \times {\mathcal {AI}}(\Lambda )\right )$
is known unconditionally due to [Reference Arthur3
Reference Bump and Ginzburg7, Theorem 1.1], so the square root of the central value is unambiguous, independent of the truth of any unproven hypothesis.
$L\left (\tfrac 12, \pi \times {\mathcal {AI}}(\Lambda )\right )$
is known unconditionally due to [Reference Arthur3
Reference Bump and Ginzburg7, Theorem 1.1], so the square root of the central value is unambiguous, independent of the truth of any unproven hypothesis.
6.2. Local computation
For
![]() $\mathrm {Re}(s)>1$
, the L-function
$\mathrm {Re}(s)>1$
, the L-function
![]() $L(s,\pi )$
is given by
$L(s,\pi )$
is given by
 $$ \begin{align*} L(s, \pi)= \prod_{p} L\left(s,\pi_p\right), \quad L\left(s,\pi_p\right)= \left(1-\frac{\alpha_p}{p^s} \right)^{-1} \left(1-\frac{\alpha_p^{-1}}{p^s} \right)^{-1} \left(1-\frac{\beta_p}{p^s} \right)^{-1} \left(1-\frac{\beta_p^{-1}}{p^s} \right)^{-1}, \end{align*} $$
$$ \begin{align*} L(s, \pi)= \prod_{p} L\left(s,\pi_p\right), \quad L\left(s,\pi_p\right)= \left(1-\frac{\alpha_p}{p^s} \right)^{-1} \left(1-\frac{\alpha_p^{-1}}{p^s} \right)^{-1} \left(1-\frac{\beta_p}{p^s} \right)^{-1} \left(1-\frac{\beta_p^{-1}}{p^s} \right)^{-1}, \end{align*} $$
for
![]() $p\nmid N$
, where
$p\nmid N$
, where
 $\mathcal S_p(\pi )=\left \{\alpha _p, \alpha _p^{-1},\beta _p, \beta _p^{-1}\right \}$
are the Satake parameters of
$\mathcal S_p(\pi )=\left \{\alpha _p, \alpha _p^{-1},\beta _p, \beta _p^{-1}\right \}$
are the Satake parameters of
![]() $\pi $
and it is known that
$\pi $
and it is known that
![]() $\left \lvert \alpha _p\right \rvert = \left \lvert \beta _p\right \rvert =1$
by [Reference Weissauer68]. Also, given
$\left \lvert \alpha _p\right \rvert = \left \lvert \beta _p\right \rvert =1$
by [Reference Weissauer68]. Also, given
![]() $\Lambda \in \widehat {\operatorname {Cl}_K}$
, we have, for
$\Lambda \in \widehat {\operatorname {Cl}_K}$
, we have, for
![]() $\mathrm {Re}(s)>1$
,
$\mathrm {Re}(s)>1$
,
 $$ \begin{align*} L(s, \mathcal{AI}(\Lambda))= \prod_{p} L\left(s, \mathcal{AI}\left(\Lambda_p\right)\right), \qquad L\left(s, \mathcal{AI}\left(\Lambda_p\right)\right)=\left(1-\frac{\alpha_{\Lambda_p}}{p^s} \right)^{-1} \left(1-\frac{\beta_{\Lambda_p}}{p^s} \right)^{-1}, \end{align*} $$
$$ \begin{align*} L(s, \mathcal{AI}(\Lambda))= \prod_{p} L\left(s, \mathcal{AI}\left(\Lambda_p\right)\right), \qquad L\left(s, \mathcal{AI}\left(\Lambda_p\right)\right)=\left(1-\frac{\alpha_{\Lambda_p}}{p^s} \right)^{-1} \left(1-\frac{\beta_{\Lambda_p}}{p^s} \right)^{-1}, \end{align*} $$
for
![]() $p \nmid N$
, where the Satake parameters
$p \nmid N$
, where the Satake parameters
 $\mathcal S_p({\mathcal {AI}}(\Lambda ))=\left \{\alpha _{\Lambda _p}, \beta _{\Lambda _p}\right \}$
satisfy the following:
$\mathcal S_p({\mathcal {AI}}(\Lambda ))=\left \{\alpha _{\Lambda _p}, \beta _{\Lambda _p}\right \}$
satisfy the following:
-
• If
 $\left ( \frac {d}{p} \right ) =1$
, then
$\left ( \frac {d}{p} \right ) =1$
, then
 $p \mathcal O_k=\mathfrak p \overline {\mathfrak p}$
and
$p \mathcal O_k=\mathfrak p \overline {\mathfrak p}$
and
 $\alpha _{\Lambda _p}=\Lambda (\mathfrak p)$
,
$\alpha _{\Lambda _p}=\Lambda (\mathfrak p)$
,
 $\beta _{\Lambda _p}=\Lambda \left (\overline {\mathfrak p}\right )=\overline {\alpha _{\Lambda _p}}$
.
$\beta _{\Lambda _p}=\Lambda \left (\overline {\mathfrak p}\right )=\overline {\alpha _{\Lambda _p}}$
. -
• If
 $\left ( \frac {d}{p} \right ) =-1$
, then
$\left ( \frac {d}{p} \right ) =-1$
, then
 $\alpha _{\Lambda _p}=1$
and
$\alpha _{\Lambda _p}=1$
and
 $\beta _{\Lambda _p}=-1$
.
$\beta _{\Lambda _p}=-1$
. -
• If
 $p\mid d$
, then
$p\mid d$
, then
 $p \mathcal O_k=\mathfrak p^2$
and
$p \mathcal O_k=\mathfrak p^2$
and
 $\alpha _{\Lambda _{p}}=\Lambda (\mathfrak p)$
,
$\alpha _{\Lambda _{p}}=\Lambda (\mathfrak p)$
,
 $\beta _{\Lambda _p}=0$
.
$\beta _{\Lambda _p}=0$
.
In this notation, we have that the Satake parameters of
![]() $L(s, \operatorname {std}(\pi ))$
and
$L(s, \operatorname {std}(\pi ))$
and
![]() $L(s, \mathrm {ad}(\pi ))$
are respectively given by
$L(s, \mathrm {ad}(\pi ))$
are respectively given by
 $$ \begin{align*} \mathcal S_{p}(\mathrm{std}(\pi)) & =\left\{ 1, \alpha_p\beta_p, \alpha_p \beta_p^{-1}, \alpha_p^{-1} \beta_p, \alpha_p^{-1} \beta_p^{-1}\right\} \\ \mathcal S_{p}(\mathrm{ad}(\pi)) & = \left\{ \alpha_p^2,\alpha_p^{-2}, \beta_p^2, \beta_p^{-2}, \alpha_p \beta_p, \alpha_p^{-1} \beta_p, \alpha_p\beta_p^{-1}, \alpha_p^{-1} \beta_p^{-1},1,1\right\}. \end{align*} $$
$$ \begin{align*} \mathcal S_{p}(\mathrm{std}(\pi)) & =\left\{ 1, \alpha_p\beta_p, \alpha_p \beta_p^{-1}, \alpha_p^{-1} \beta_p, \alpha_p^{-1} \beta_p^{-1}\right\} \\ \mathcal S_{p}(\mathrm{ad}(\pi)) & = \left\{ \alpha_p^2,\alpha_p^{-2}, \beta_p^2, \beta_p^{-2}, \alpha_p \beta_p, \alpha_p^{-1} \beta_p, \alpha_p\beta_p^{-1}, \alpha_p^{-1} \beta_p^{-1},1,1\right\}. \end{align*} $$
For
![]() $\star \in \{ \pi , {\mathcal {AI}}(\Lambda ), \mathrm {std}(\pi ), \mathrm {ad}(\pi ) \} $
and
$\star \in \{ \pi , {\mathcal {AI}}(\Lambda ), \mathrm {std}(\pi ), \mathrm {ad}(\pi ) \} $
and
![]() $p \nmid N$
, define
$p \nmid N$
, define
 $$ \begin{align*} a_{\star}(p^n)=\sum_{\alpha \in \mathcal S_{p}(\star)} \alpha^n. \end{align*} $$
$$ \begin{align*} a_{\star}(p^n)=\sum_{\alpha \in \mathcal S_{p}(\star)} \alpha^n. \end{align*} $$
Also, for
![]() $f,g \in \{ \pi , {\mathcal {AI}}(\Lambda ), \mathrm {std}(\pi ), \mathrm {ad}(\pi ) \}$
, let
$f,g \in \{ \pi , {\mathcal {AI}}(\Lambda ), \mathrm {std}(\pi ), \mathrm {ad}(\pi ) \}$
, let
![]() $a_{f \times g}(p^n)=a_{f}(p^n)a_{g}(p^n)$
and
$a_{f \times g}(p^n)=a_{f}(p^n)a_{g}(p^n)$
and
![]() $a_{f \times \chi _d}(p^n)=a_{f}(p^n) \chi _d(p^n)$
.
$a_{f \times \chi _d}(p^n)=a_{f}(p^n) \chi _d(p^n)$
.
We now make the following observations. First, using
![]() $\left \lvert \alpha _p\right \rvert =\left \lvert \beta _p\right \rvert =1$
, it immediately follows that for any
$\left \lvert \alpha _p\right \rvert =\left \lvert \beta _p\right \rvert =1$
, it immediately follows that for any
![]() $n \ge 1$
and
$n \ge 1$
and
![]() $p \nmid N$
,
$p \nmid N$
,
 $$ \begin{align} \left\lvert a_{\pi \times {\mathcal{AI}}(\Lambda)}(p^n) \right\rvert \le 8. \end{align} $$
$$ \begin{align} \left\lvert a_{\pi \times {\mathcal{AI}}(\Lambda)}(p^n) \right\rvert \le 8. \end{align} $$
Additionally, observe for
![]() $p\nmid N$
that
$p\nmid N$
that
 $$ \begin{align*} a_{\mathrm{ad}(\pi)}(p) = \alpha_p^2+\alpha_p^{-2}+\beta_p^{2}+\beta_p^{-2}+a_{\operatorname{std}(\pi)}(p)+1. \end{align*} $$
$$ \begin{align*} a_{\mathrm{ad}(\pi)}(p) = \alpha_p^2+\alpha_p^{-2}+\beta_p^{2}+\beta_p^{-2}+a_{\operatorname{std}(\pi)}(p)+1. \end{align*} $$
Hence, for
![]() $p \nmid N$
,
$p \nmid N$
,
 $$ \begin{align} a_{\pi}\left(p^2\right)= a_{\mathrm{ad}(\pi)}(p) -a_{\mathrm{std}(\pi)}(p)-1. \end{align} $$
$$ \begin{align} a_{\pi}\left(p^2\right)= a_{\mathrm{ad}(\pi)}(p) -a_{\mathrm{std}(\pi)}(p)-1. \end{align} $$
Also for
![]() $p \nmid N$
,
$p \nmid N$
,
 $$ \begin{align} a_{\pi}(p)^2&=\alpha_p^2+\alpha_p^{-2}+\beta_p^{2}+\beta_p^{-2}+2\left(\alpha_p+\alpha_p^{-1}\right)\left(\beta_p+\beta_p^{-1}\right)+4 \nonumber\\ &= a_{\mathrm{ad}(\pi)}(p)+a_{\mathrm{std}(\pi)}(p)+1. \end{align} $$
$$ \begin{align} a_{\pi}(p)^2&=\alpha_p^2+\alpha_p^{-2}+\beta_p^{2}+\beta_p^{-2}+2\left(\alpha_p+\alpha_p^{-1}\right)\left(\beta_p+\beta_p^{-1}\right)+4 \nonumber\\ &= a_{\mathrm{ad}(\pi)}(p)+a_{\mathrm{std}(\pi)}(p)+1. \end{align} $$
Recall that for
 $\left (\frac {d}{p} \right )\neq -1$
, we have
$\left (\frac {d}{p} \right )\neq -1$
, we have
 $\alpha _{\Lambda _p}^2=\Lambda ^2(\mathfrak p)=\alpha _{\Lambda _p^2}$
. Thus, we get that for
$\alpha _{\Lambda _p}^2=\Lambda ^2(\mathfrak p)=\alpha _{\Lambda _p^2}$
. Thus, we get that for
![]() $p \nmid N$
,
$p \nmid N$
,
 $$ \begin{align*} a_{{\mathcal{AI}}(\Lambda)}\left(p^2\right) = a_{{\mathcal{AI}}\left(\Lambda^2\right)}(p)+\left(\frac{d}{p} \right)^2-\left(\frac{d}{p} \right) = \begin{cases} \alpha_{\Lambda_p^2}+\beta_{\Lambda_p^2} & \text{if } \left( \frac{d}{p} \right) \neq -1,\\ 2 & \text{if } \left( \frac{d}{p} \right) =-1. \end{cases} \end{align*} $$
$$ \begin{align*} a_{{\mathcal{AI}}(\Lambda)}\left(p^2\right) = a_{{\mathcal{AI}}\left(\Lambda^2\right)}(p)+\left(\frac{d}{p} \right)^2-\left(\frac{d}{p} \right) = \begin{cases} \alpha_{\Lambda_p^2}+\beta_{\Lambda_p^2} & \text{if } \left( \frac{d}{p} \right) \neq -1,\\ 2 & \text{if } \left( \frac{d}{p} \right) =-1. \end{cases} \end{align*} $$
Therefore, combining this equation with equation (60), we conclude that
 $$ \begin{align} a_{\pi \times {\mathcal{AI}}(\Lambda)}\left(p^2\right)=\left(a_{\mathrm{ad}(\pi)}(p) -a_{\mathrm{std}(\pi)}(p)-1\right) \left(a_{{\mathcal{AI}}\left(\Lambda^2\right)}(p)+\left( \frac{d}{p}\right)^2-\left(\frac{d}{p} \right) \right). \end{align} $$
$$ \begin{align} a_{\pi \times {\mathcal{AI}}(\Lambda)}\left(p^2\right)=\left(a_{\mathrm{ad}(\pi)}(p) -a_{\mathrm{std}(\pi)}(p)-1\right) \left(a_{{\mathcal{AI}}\left(\Lambda^2\right)}(p)+\left( \frac{d}{p}\right)^2-\left(\frac{d}{p} \right) \right). \end{align} $$
6.3. Preliminary lemmas
Soundararajan’s method for moments of L-functions starts with a remarkable bound for the central L-value given in terms of a Dirichlet polynomial supported on prime powers. This inequality has been generalized by Chandee [Reference Choie, Gun and Kohnen11].
Lemma 6.2. Assume the GRH for
![]() $L(s,\pi \times {\mathcal {AI}}(\Lambda ))$
. There exists
$L(s,\pi \times {\mathcal {AI}}(\Lambda ))$
. There exists
![]() $C_0>1$
, which depends at most on
$C_0>1$
, which depends at most on
![]() $N,k$
such that for
$N,k$
such that for
![]() $x \ge 2$
,
$x \ge 2$
,
 $$ \begin{align*} \log L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right) \le \sum_{\substack{p^n \le x \\ p \nmid N}} \frac{a_{\pi \times {\mathcal{AI}}(\Lambda)}(p^n)}{n p^{\frac{n}{2}\left(1+1/\log x\right)}} + \frac{C_0 \log \lvert d\rvert}{\log x}. \end{align*} $$
$$ \begin{align*} \log L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right) \le \sum_{\substack{p^n \le x \\ p \nmid N}} \frac{a_{\pi \times {\mathcal{AI}}(\Lambda)}(p^n)}{n p^{\frac{n}{2}\left(1+1/\log x\right)}} + \frac{C_0 \log \lvert d\rvert}{\log x}. \end{align*} $$
Remark 6.3. Taking
![]() $x= \log \lvert d\rvert $
and using the bound (59), it follows that
$x= \log \lvert d\rvert $
and using the bound (59), it follows that
 $$ \begin{align*} L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right) \ll \exp\left(2C_0 \frac{\log \lvert d\rvert}{\log \log \lvert d\rvert} \right). \end{align*} $$
$$ \begin{align*} L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right) \ll \exp\left(2C_0 \frac{\log \lvert d\rvert}{\log \log \lvert d\rvert} \right). \end{align*} $$
Proof. This follows immediately from [Reference Choie, Gun and Kohnen11, Theorem 2.1].
To analyze the foregoing sum over prime powers, we will separately consider the primes, squares of primes, and higher prime powers. The contribution of the squares of primes is estimated in the following result:
Lemma 6.4. Assume the GRH. Then for
![]() $x \ge 2$
, the following hold:
$x \ge 2$
, the following hold:
-
i)
 $\displaystyle \sum _{\substack {p \le \sqrt {x} \\ p \nmid N}} \frac {a_{\pi \times {\mathcal {AI}}(\Lambda )}\left (p^2\right )}{p^{1+2/\log x}} \frac {\log x/p}{\log x}=-\log \log x(1+o(1))+O_{\pi } \left ( \log \log \log \lvert d\rvert \right )$
and
$\displaystyle \sum _{\substack {p \le \sqrt {x} \\ p \nmid N}} \frac {a_{\pi \times {\mathcal {AI}}(\Lambda )}\left (p^2\right )}{p^{1+2/\log x}} \frac {\log x/p}{\log x}=-\log \log x(1+o(1))+O_{\pi } \left ( \log \log \log \lvert d\rvert \right )$
and -
ii)
 $\displaystyle \sum _{\substack {p \le x \\ p\nmid N, \left ( \frac {d}{p}\right )=1 }} \frac {a_{\pi }(p)^2}{p}= \frac 12 \log \log x(1+o(1))+O_{\pi }(\log \log \log \lvert d\rvert )$
.
$\displaystyle \sum _{\substack {p \le x \\ p\nmid N, \left ( \frac {d}{p}\right )=1 }} \frac {a_{\pi }(p)^2}{p}= \frac 12 \log \log x(1+o(1))+O_{\pi }(\log \log \log \lvert d\rvert )$
.
Remark 6.5. We assume that the GRH holds for
![]() $L(s,\chi _d)$
,
$L(s,\chi _d)$
,
![]() $L(s, \pi \times {\mathcal {AI}}(\Lambda ))$
,
$L(s, \pi \times {\mathcal {AI}}(\Lambda ))$
,
 $L\left (s, \mathrm {ad}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
,
$L\left (s, \mathrm {ad}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
,
![]() $L(s, \mathrm {ad}(\pi ) \times \chi _d)$
,
$L(s, \mathrm {ad}(\pi ) \times \chi _d)$
,
 $L\left (s, \mathrm {std}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
, and
$L\left (s, \mathrm {std}(\pi ) \times {\mathcal {AI}}\left (\Lambda ^2\right )\right )$
, and
![]() $L(s, \mathrm {std}(\pi ) \times \chi _d)$
.
$L(s, \mathrm {std}(\pi ) \times \chi _d)$
.
Proof. Using
![]() $\left \lvert \alpha _p\right \rvert =\left \lvert \beta _p\right \rvert =1$
, we get, for
$\left \lvert \alpha _p\right \rvert =\left \lvert \beta _p\right \rvert =1$
, we get, for
![]() $x \ge (\log \lvert d\rvert )^3$
,
$x \ge (\log \lvert d\rvert )^3$
,
 $$ \begin{align*} \sum_{\substack{p \le x \\ p \nmid N}} \frac{a_{\mathrm{std}(\pi) \times \chi_d}(p)}{p}=\sum_{\substack{ (\log \lvert d\rvert)^3 \le p \le x \\ p \nmid N}} \frac{a_{\mathrm{std}(\pi) \times \chi_d}(p)}{p}+O(\log \log \log \lvert d\rvert). \end{align*} $$
$$ \begin{align*} \sum_{\substack{p \le x \\ p \nmid N}} \frac{a_{\mathrm{std}(\pi) \times \chi_d}(p)}{p}=\sum_{\substack{ (\log \lvert d\rvert)^3 \le p \le x \\ p \nmid N}} \frac{a_{\mathrm{std}(\pi) \times \chi_d}(p)}{p}+O(\log \log \log \lvert d\rvert). \end{align*} $$
By Proposition 5.4,
![]() $L(s, \mathrm {std}(\pi ) \times \chi _d)$
belongs to the extended Selberg class, so that we may use [Reference Böcherer and Das5, Lemma 5]. Applying this lemma twice, it follows that the sum on the right-hand side is
$L(s, \mathrm {std}(\pi ) \times \chi _d)$
belongs to the extended Selberg class, so that we may use [Reference Böcherer and Das5, Lemma 5]. Applying this lemma twice, it follows that the sum on the right-hand side is
![]() $O_{\pi }(1)$
, and so
$O_{\pi }(1)$
, and so
 $$ \begin{align*} \sum_{\substack{p \le x \\ p \nmid N}} \frac{a_{\mathrm{std}(\pi)}(p) \left(\frac{d}{p}\right)}{p} \ll_{\pi} \log \log \log \lvert d\rvert. \end{align*} $$
$$ \begin{align*} \sum_{\substack{p \le x \\ p \nmid N}} \frac{a_{\mathrm{std}(\pi)}(p) \left(\frac{d}{p}\right)}{p} \ll_{\pi} \log \log \log \lvert d\rvert. \end{align*} $$
Repeating the foregoing above and recalling Remark 5.8, it follows that for
 $\star \in \left \{ \mathrm {ad}(\pi ) \times \chi _d, \mathrm {ad}(\pi ) \times {\mathcal {AI}}\left ( \Lambda ^2\right ), \mathrm {std}(\pi )\times {\mathcal {AI}}\left (\Lambda ^2\right ), {\mathcal {AI}}\left (\Lambda ^2\right )\right \}$
, we have
$\star \in \left \{ \mathrm {ad}(\pi ) \times \chi _d, \mathrm {ad}(\pi ) \times {\mathcal {AI}}\left ( \Lambda ^2\right ), \mathrm {std}(\pi )\times {\mathcal {AI}}\left (\Lambda ^2\right ), {\mathcal {AI}}\left (\Lambda ^2\right )\right \}$
, we have
 $ \sum _{\substack {p \le x \\ p\nmid N}} \frac {a_{\star }(p)}{p} \ll \log \log \log \lvert d\rvert. $
Also,
$ \sum _{\substack {p \le x \\ p\nmid N}} \frac {a_{\star }(p)}{p} \ll \log \log \log \lvert d\rvert. $
Also,
 $\sum _{p\mid d} \frac {1}{p} \ll \log \log \log \lvert d\rvert $
, and under the GRH we have
$\sum _{p\mid d} \frac {1}{p} \ll \log \log \log \lvert d\rvert $
, and under the GRH we have
 $\sum _{p \le x} \frac {\chi _d(p)}{p} \ll \log \log \log \lvert d\rvert $
. Finally, using the fact that
$\sum _{p \le x} \frac {\chi _d(p)}{p} \ll \log \log \log \lvert d\rvert $
. Finally, using the fact that
![]() $L(s,\mathrm {std}(\pi ))$
and
$L(s,\mathrm {std}(\pi ))$
and
![]() $L(s,\mathrm {ad}(\pi ))$
do not vanish on the line
$L(s,\mathrm {ad}(\pi ))$
do not vanish on the line
![]() $\mathrm {Re}(s)=1$
– the latter of which follows from Proposition 5.4 – we have that (see, e.g., [Reference Kim31, Theorem 1])
$\mathrm {Re}(s)=1$
– the latter of which follows from Proposition 5.4 – we have that (see, e.g., [Reference Kim31, Theorem 1])
 $$ \begin{align*} \sum_{\substack{p \le x \\ p\nmid N}} \frac{a_{\mathrm{ad}(\pi)}(p)}{p} =o(\log \log x), \qquad \sum_{\substack{p \le x \\ p\nmid N}} \frac{a_{\mathrm{std}(\pi)}(p)}{p} =o(\log \log x). \end{align*} $$
$$ \begin{align*} \sum_{\substack{p \le x \\ p\nmid N}} \frac{a_{\mathrm{ad}(\pi)}(p)}{p} =o(\log \log x), \qquad \sum_{\substack{p \le x \\ p\nmid N}} \frac{a_{\mathrm{std}(\pi)}(p)}{p} =o(\log \log x). \end{align*} $$
Therefore, applying equation (62) and using the foregoing estimates along with partial summation to handle the smooth weight
 $p^{-2/\log x} \frac {\log x/p}{\log x}$
completes the proof of (i).
$p^{-2/\log x} \frac {\log x/p}{\log x}$
completes the proof of (i).
To prove (ii), we rewrite the condition
 $\left ( \frac {d}{p} \right )=1$
as
$\left ( \frac {d}{p} \right )=1$
as
 $\frac {1}{2}\left (\left (\frac {d}{p}\right )+1\right )$
for
$\frac {1}{2}\left (\left (\frac {d}{p}\right )+1\right )$
for
![]() $p \nmid d$
, use equation (61) and argue as before. We trivially bound the contribution of
$p \nmid d$
, use equation (61) and argue as before. We trivially bound the contribution of
![]() $p\mid d$
by
$p\mid d$
by
 $ \le 16 \sum _{p\mid d}\frac {1}{p} \ll \log \log \log \lvert d\rvert. $
$ \le 16 \sum _{p\mid d}\frac {1}{p} \ll \log \log \log \lvert d\rvert. $
6.4. Large deviations of Dirichlet polynomials
To bound the frequency with which large values of
 $\log L\left (\tfrac 12, \pi \times {\mathcal {AI}}(\Lambda )\right )$
occur, we will estimate large deviations of the sum over primes in Lemma 6.2 by bounding its moments. This is done in the following fairly standard lemma (e.g. [Reference Saha and Schmidt64, Lemma 3]), whose proof we include for completeness:
$\log L\left (\tfrac 12, \pi \times {\mathcal {AI}}(\Lambda )\right )$
occur, we will estimate large deviations of the sum over primes in Lemma 6.2 by bounding its moments. This is done in the following fairly standard lemma (e.g. [Reference Saha and Schmidt64, Lemma 3]), whose proof we include for completeness:
Lemma 6.6. Let
 $\left \{b_p\right \}_p \subset \mathbb R$
and
$\left \{b_p\right \}_p \subset \mathbb R$
and
![]() $\ell \in \mathbb N$
. Suppose
$\ell \in \mathbb N$
. Suppose
 $x^{\ell } < \sqrt {\lvert d\rvert }/2$
. Then the following hold:
$x^{\ell } < \sqrt {\lvert d\rvert }/2$
. Then the following hold:
-
i)
 $ \displaystyle \frac {1}{\lvert \operatorname {Cl}_K\rvert } \sum _{\Lambda \in \widehat {\operatorname {Cl}_K}} \left ( \sum _{\substack {p \le x \\ p \nmid d, p \nmid N}} \frac {b_p a_{{\mathcal {AI}}(\Lambda )}(p)}{\sqrt {p}}\right )^{2\ell } \le \frac {(2\ell )!}{2^{\ell } \ell !} \left ( 2 \sum _{\substack {p \le x \\ \left ( \frac {d}{p}\right ) =1, p \nmid N}} \frac {b_p^2}{p}\right )^{\ell }$
and
$ \displaystyle \frac {1}{\lvert \operatorname {Cl}_K\rvert } \sum _{\Lambda \in \widehat {\operatorname {Cl}_K}} \left ( \sum _{\substack {p \le x \\ p \nmid d, p \nmid N}} \frac {b_p a_{{\mathcal {AI}}(\Lambda )}(p)}{\sqrt {p}}\right )^{2\ell } \le \frac {(2\ell )!}{2^{\ell } \ell !} \left ( 2 \sum _{\substack {p \le x \\ \left ( \frac {d}{p}\right ) =1, p \nmid N}} \frac {b_p^2}{p}\right )^{\ell }$
and -
ii)
 $\displaystyle \frac {1}{\lvert \operatorname {Cl}_K\rvert } \sum _{\Lambda \in \widehat {\operatorname {Cl}_K}} \left ( \sum _{\substack {p \le x \\ p \mid d, p \nmid N}} \frac {b_p a_{{\mathcal {AI}}(\Lambda )}(p)}{\sqrt {p}}\right )^{2\ell } \le \frac {(2\ell )!}{2^{\ell } \ell !} \left ( \sum _{\substack {p \le x \\ p\mid d, p \nmid N}} \frac {b_p^2}{p}\right )^{\ell }.$
$\displaystyle \frac {1}{\lvert \operatorname {Cl}_K\rvert } \sum _{\Lambda \in \widehat {\operatorname {Cl}_K}} \left ( \sum _{\substack {p \le x \\ p \mid d, p \nmid N}} \frac {b_p a_{{\mathcal {AI}}(\Lambda )}(p)}{\sqrt {p}}\right )^{2\ell } \le \frac {(2\ell )!}{2^{\ell } \ell !} \left ( \sum _{\substack {p \le x \\ p\mid d, p \nmid N}} \frac {b_p^2}{p}\right )^{\ell }.$
Proof. Let
 $b_n = \prod _{p^j \mathrel {\Vert } n} b_p^j$
. We have
$b_n = \prod _{p^j \mathrel {\Vert } n} b_p^j$
. We have
 $$ \begin{align} &\frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{\operatorname{Cl}_K}} \left( \sum_{\substack{p \le x \\ p \nmid d, p\nmid N}} \frac{b_p a_{{\mathcal{AI}}(\Lambda)}(p)}{\sqrt{p}}\right)^{2\ell} \nonumber \\ &\quad = \sum_{\substack{n \ge 1 \\ \left(n,N\right)=1}} \frac{b_n}{\sqrt{n}} \sum_{\substack{ \mathfrak p_1 , \dotsc, \mathfrak p_{2\ell} \subset \mathcal O_K \\ N\left(\mathfrak p_1 \dotsm \mathfrak p_{2\ell}\right)=n \\ N\left(\mathfrak p_j\right) \le x \\ \mathfrak p_j \text{ split }}} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{\operatorname{Cl}_K}} \prod_{j=1}^{2\ell} \left(\Lambda\left(\mathfrak p_j\right)+\Lambda\left(\mathfrak p_j\right)^{-1} \right). \end{align} $$
$$ \begin{align} &\frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{\operatorname{Cl}_K}} \left( \sum_{\substack{p \le x \\ p \nmid d, p\nmid N}} \frac{b_p a_{{\mathcal{AI}}(\Lambda)}(p)}{\sqrt{p}}\right)^{2\ell} \nonumber \\ &\quad = \sum_{\substack{n \ge 1 \\ \left(n,N\right)=1}} \frac{b_n}{\sqrt{n}} \sum_{\substack{ \mathfrak p_1 , \dotsc, \mathfrak p_{2\ell} \subset \mathcal O_K \\ N\left(\mathfrak p_1 \dotsm \mathfrak p_{2\ell}\right)=n \\ N\left(\mathfrak p_j\right) \le x \\ \mathfrak p_j \text{ split }}} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{\operatorname{Cl}_K}} \prod_{j=1}^{2\ell} \left(\Lambda\left(\mathfrak p_j\right)+\Lambda\left(\mathfrak p_j\right)^{-1} \right). \end{align} $$
For
![]() $n \in \mathbb N$
in this sum, write
$n \in \mathbb N$
in this sum, write
![]() $n=q_1^{e_1} \dotsm q_r^{e_r}$
, where
$n=q_1^{e_1} \dotsm q_r^{e_r}$
, where
![]() $q_1, \dotsc , q_r$
are distinct primes with
$q_1, \dotsc , q_r$
are distinct primes with
![]() $q_j \mathcal O_K=\mathfrak q_j \overline {\mathfrak q_j}$
for each
$q_j \mathcal O_K=\mathfrak q_j \overline {\mathfrak q_j}$
for each
![]() $j=1,\dotsc , r$
. The inner sum on the right-hand side equals
$j=1,\dotsc , r$
. The inner sum on the right-hand side equals
 $$ \begin{align*} \sum_{\substack{0 \le f_1\le e_1 }} \dotsm \sum_{0 \le f_r \le e_r}\binom{e_1}{f_1} \dotsm \binom{e_r}{f_r} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{\operatorname{Cl}_K}} \Lambda\left( \mathfrak q_1^{f_1} \overline{ \mathfrak q_1}^{e_1-f_1} \dotsm \mathfrak q_r^{f_r} \overline{ \mathfrak q_r}^{e_r-f_r} \right). \end{align*} $$
$$ \begin{align*} \sum_{\substack{0 \le f_1\le e_1 }} \dotsm \sum_{0 \le f_r \le e_r}\binom{e_1}{f_1} \dotsm \binom{e_r}{f_r} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{\operatorname{Cl}_K}} \Lambda\left( \mathfrak q_1^{f_1} \overline{ \mathfrak q_1}^{e_1-f_1} \dotsm \mathfrak q_r^{f_r} \overline{ \mathfrak q_r}^{e_r-f_r} \right). \end{align*} $$
Write
 $\mathfrak a= \mathfrak q_1^{f_1} \overline { \mathfrak q_1}^{e_1-f_1} \dotsm \mathfrak q_r^{f_r} \overline { \mathfrak q_r}^{e_r-f_r} $
. Since
$\mathfrak a= \mathfrak q_1^{f_1} \overline { \mathfrak q_1}^{e_1-f_1} \dotsm \mathfrak q_r^{f_r} \overline { \mathfrak q_r}^{e_r-f_r} $
. Since
![]() $N(\mathfrak a) \le x^{2\ell } < \lvert d\rvert /4$
, the inner sum is zero unless
$N(\mathfrak a) \le x^{2\ell } < \lvert d\rvert /4$
, the inner sum is zero unless
![]() $\mathfrak a=(\alpha )$
and
$\mathfrak a=(\alpha )$
and
![]() $\alpha \in \mathbb Z$
. Hence the only terms that do not vanish are those with
$\alpha \in \mathbb Z$
. Hence the only terms that do not vanish are those with
![]() $e_1, \dotsc , e_r$
even and
$e_1, \dotsc , e_r$
even and
![]() $f_j=e_j/2$
for
$f_j=e_j/2$
for
![]() $j=1,\dotsc , r$
. Define the multiplicative functions
$j=1,\dotsc , r$
. Define the multiplicative functions
![]() $\nu (n)$
by
$\nu (n)$
by
![]() $\nu (p^a)=1/a!$
and
$\nu (p^a)=1/a!$
and
![]() $g(n)$
by
$g(n)$
by
 $g(p^a)=\binom {a}{a/2}$
if
$g(p^a)=\binom {a}{a/2}$
if
![]() $2\mid a$
and
$2\mid a$
and
![]() $g(p^a)=0$
otherwise. The right-hand side of equation (63) equals
$g(p^a)=0$
otherwise. The right-hand side of equation (63) equals
 $$ \begin{align*} (2\ell!) \sum_{\substack{p\mid n \Rightarrow p \le x, p\nmid N, \left(\frac{d}{p}\right)=1 \\ \Omega(n)=2\ell}} \frac{b_n \nu(n) g(n)}{\sqrt{n}} \le \frac{(2\ell!)}{2^{\ell} \ell!} \left( 2 \sum_{\substack{p \le x \\ \left(\frac{d}{p}\right)=1, p \nmid N }} \frac{b_p^2}{p}\right)^{\ell}, \end{align*} $$
$$ \begin{align*} (2\ell!) \sum_{\substack{p\mid n \Rightarrow p \le x, p\nmid N, \left(\frac{d}{p}\right)=1 \\ \Omega(n)=2\ell}} \frac{b_n \nu(n) g(n)}{\sqrt{n}} \le \frac{(2\ell!)}{2^{\ell} \ell!} \left( 2 \sum_{\substack{p \le x \\ \left(\frac{d}{p}\right)=1, p \nmid N }} \frac{b_p^2}{p}\right)^{\ell}, \end{align*} $$
where for the last inequality we used the facts that the sum on the left-hand side is supported on squares and
 $ \nu \left (m^2\right )g\left (m^2\right )\le \nu (m)$
. This completes the proof of (i).
$ \nu \left (m^2\right )g\left (m^2\right )\le \nu (m)$
. This completes the proof of (i).
Similarly, we have
 $$ \begin{align*} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{\operatorname{Cl}_K}} \left( \sum_{\substack{p \le x \\ p \mid d, p \nmid N}} \frac{b_p a_{{\mathcal{AI}}(\Lambda)}(p)}{\sqrt{p}}\right)^{2\ell}= \sum_{n \ge 1} \frac{b_n}{\sqrt{n}} \sum_{\substack{ \mathfrak p_1 , \dotsc, \mathfrak p_{2\ell} \subset \mathcal O_K \\ N\left(\mathfrak p_1 \dotsm \mathfrak p_{2\ell}\right)=n \\ N\left(\mathfrak p_j\right) \le x \\ \mathfrak p_j \text{ ramified }}} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{\operatorname{Cl}_K}} \Lambda\left(\mathfrak p_1 \dotsm \mathfrak p_{2\ell}\right). \end{align*} $$
$$ \begin{align*} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{\operatorname{Cl}_K}} \left( \sum_{\substack{p \le x \\ p \mid d, p \nmid N}} \frac{b_p a_{{\mathcal{AI}}(\Lambda)}(p)}{\sqrt{p}}\right)^{2\ell}= \sum_{n \ge 1} \frac{b_n}{\sqrt{n}} \sum_{\substack{ \mathfrak p_1 , \dotsc, \mathfrak p_{2\ell} \subset \mathcal O_K \\ N\left(\mathfrak p_1 \dotsm \mathfrak p_{2\ell}\right)=n \\ N\left(\mathfrak p_j\right) \le x \\ \mathfrak p_j \text{ ramified }}} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{\operatorname{Cl}_K}} \Lambda\left(\mathfrak p_1 \dotsm \mathfrak p_{2\ell}\right). \end{align*} $$
Write
![]() $\mathfrak a=\mathfrak p_1 \dotsm \mathfrak p_{2\ell }$
. The inner sum is zero unless
$\mathfrak a=\mathfrak p_1 \dotsm \mathfrak p_{2\ell }$
. The inner sum is zero unless
![]() $\mathfrak a=(\alpha )$
with
$\mathfrak a=(\alpha )$
with
![]() $\alpha \in \mathbb Z$
, since
$\alpha \in \mathbb Z$
, since
![]() $N(\mathfrak a ) < \lvert d\rvert /4$
. Consequently, n is a square. The right-hand side equals
$N(\mathfrak a ) < \lvert d\rvert /4$
. Consequently, n is a square. The right-hand side equals
 $$ \begin{align*} (2\ell)!\sum_{\substack{p\mid n \Rightarrow p \le x, p \nmid N, p \mid d \\ \Omega(n)=\ell}} \frac{b_n^2}{n} \nu\left(n^2\right) \le \frac{(2\ell)!}{2^{\ell} \ell!} \left( \sum_{\substack{p \le x \\ p\mid d, p \nmid N}} \frac{b_p^2}{p}\right)^{\ell}, \end{align*} $$
$$ \begin{align*} (2\ell)!\sum_{\substack{p\mid n \Rightarrow p \le x, p \nmid N, p \mid d \\ \Omega(n)=\ell}} \frac{b_n^2}{n} \nu\left(n^2\right) \le \frac{(2\ell)!}{2^{\ell} \ell!} \left( \sum_{\substack{p \le x \\ p\mid d, p \nmid N}} \frac{b_p^2}{p}\right)^{\ell}, \end{align*} $$
where we used the fact that
 $\nu (n^2) \le \frac {\nu (n)}{2^{\Omega (n)}}$
in the last step. This completes the proof of (ii).
$\nu (n^2) \le \frac {\nu (n)}{2^{\Omega (n)}}$
in the last step. This completes the proof of (ii).
For
![]() $x \ge 2$
, let
$x \ge 2$
, let
 $ P(\Lambda ;x)= \sum _{\substack {p \le x \\ p \nmid N}} \frac {a_{\pi }(p) a_{{\mathcal {AI}}(\Lambda )}(p)}{p^{\frac 12+\frac {1}{\log x}}} \frac {\log x/p}{\log x} $
, and for
$ P(\Lambda ;x)= \sum _{\substack {p \le x \\ p \nmid N}} \frac {a_{\pi }(p) a_{{\mathcal {AI}}(\Lambda )}(p)}{p^{\frac 12+\frac {1}{\log x}}} \frac {\log x/p}{\log x} $
, and for
![]() $V\in \mathbb R$
let
$V\in \mathbb R$
let
 $ A_{K}(V;x)= \frac {1}{\lvert \operatorname {Cl}_K\rvert } \left \lvert \left \{ \Lambda \in \widehat {\operatorname {Cl}}_K : P(\Lambda ;x)> V \right \}\right \rvert. $
$ A_{K}(V;x)= \frac {1}{\lvert \operatorname {Cl}_K\rvert } \left \lvert \left \{ \Lambda \in \widehat {\operatorname {Cl}}_K : P(\Lambda ;x)> V \right \}\right \rvert. $
Lemma 6.7. Let
![]() $\epsilon>0$
be sufficiently small. Then for
$\epsilon>0$
be sufficiently small. Then for
 $(\log \log \lvert d\rvert )^{3/4}\le V \le \frac { 4C_0 \log \lvert d\rvert }{\log \log \lvert d\rvert }$
, we have
$(\log \log \lvert d\rvert )^{3/4}\le V \le \frac { 4C_0 \log \lvert d\rvert }{\log \log \lvert d\rvert }$
, we have
 $$ \begin{align*} A_{K}\left(V;\lvert d\rvert^{\frac{1}{\epsilon V}}\right) \ll_{\pi, \epsilon} \exp\left(\frac{-V^2}{2 \log \log \lvert d\rvert}(1-2\epsilon)\right)+e^{-\frac{\epsilon}{4} V \log V}. \end{align*} $$
$$ \begin{align*} A_{K}\left(V;\lvert d\rvert^{\frac{1}{\epsilon V}}\right) \ll_{\pi, \epsilon} \exp\left(\frac{-V^2}{2 \log \log \lvert d\rvert}(1-2\epsilon)\right)+e^{-\frac{\epsilon}{4} V \log V}. \end{align*} $$
Proof. Set
 $x=\lvert d\rvert ^{\frac {1}{\epsilon V}}$
and
$x=\lvert d\rvert ^{\frac {1}{\epsilon V}}$
and
![]() $z=x^{1/\log \log \lvert d\rvert }$
. Let
$z=x^{1/\log \log \lvert d\rvert }$
. Let
where
 $$ \begin{align*} P_1(\Lambda) =\sum_{\substack{p \le z \\ p \nmid d, p \nmid N}} \frac{a_{\pi}(p) a_{{\mathcal{AI}}(\Lambda)}(p)}{p^{\frac12+\frac{1}{\log x}}} \frac{\log x/p}{\log x}, \qquad P_2(\Lambda) =\sum_{\substack{ z <p \le x \\ p \nmid d, p \nmid N}} \frac{a_{\pi}(p) a_{{\mathcal{AI}}(\Lambda)}(p)}{p^{\frac12+\frac{1}{\log x}}} \frac{\log x/p}{\log x}, \end{align*} $$
$$ \begin{align*} P_1(\Lambda) =\sum_{\substack{p \le z \\ p \nmid d, p \nmid N}} \frac{a_{\pi}(p) a_{{\mathcal{AI}}(\Lambda)}(p)}{p^{\frac12+\frac{1}{\log x}}} \frac{\log x/p}{\log x}, \qquad P_2(\Lambda) =\sum_{\substack{ z <p \le x \\ p \nmid d, p \nmid N}} \frac{a_{\pi}(p) a_{{\mathcal{AI}}(\Lambda)}(p)}{p^{\frac12+\frac{1}{\log x}}} \frac{\log x/p}{\log x}, \end{align*} $$
and
![]() $P_3(\Lambda )=P(\Lambda ;x)-P_1(\Lambda )-P_2(\Lambda )$
. Let
$P_3(\Lambda )=P(\Lambda ;x)-P_1(\Lambda )-P_2(\Lambda )$
. Let
![]() $V_1=(1-\epsilon )V, V_2=\tfrac {\epsilon }{2}V$
. Clearly, if
$V_1=(1-\epsilon )V, V_2=\tfrac {\epsilon }{2}V$
. Clearly, if
![]() $P(\Lambda ;x)>V$
, then (i)
$P(\Lambda ;x)>V$
, then (i)
![]() $P_1(\Lambda )>V_1$
, (ii)
$P_1(\Lambda )>V_1$
, (ii)
![]() $P_2(\Lambda )>V_2$
, or (iii)
$P_2(\Lambda )>V_2$
, or (iii)
![]() $P_3(\Lambda )>V_2. $
By Lemma 6.6 we get that the number of
$P_3(\Lambda )>V_2. $
By Lemma 6.6 we get that the number of
![]() $\Lambda \in \widehat {\operatorname {Cl}_K}$
such that (i) holds is bounded by
$\Lambda \in \widehat {\operatorname {Cl}_K}$
such that (i) holds is bounded by
 $$ \begin{align*} \frac{1}{V_1^{2\ell}} \sum_{\Lambda \in \widehat{\operatorname{Cl}}_K} P_1(\Lambda)^{2\ell} \ll \lvert\operatorname{Cl}_K\rvert \frac{(2\ell)!}{\left(V_1^22\right)^{\ell} \ell!} \left( 2 \sum_{\substack{p \le d \\ \left(\frac{d}{p} \right)=1, p \nmid N}} \frac{a_{\pi}(p)^2}{p} \right)^{\ell}, \end{align*} $$
$$ \begin{align*} \frac{1}{V_1^{2\ell}} \sum_{\Lambda \in \widehat{\operatorname{Cl}}_K} P_1(\Lambda)^{2\ell} \ll \lvert\operatorname{Cl}_K\rvert \frac{(2\ell)!}{\left(V_1^22\right)^{\ell} \ell!} \left( 2 \sum_{\substack{p \le d \\ \left(\frac{d}{p} \right)=1, p \nmid N}} \frac{a_{\pi}(p)^2}{p} \right)^{\ell}, \end{align*} $$
provided that
 $\ell \le \frac 13 \epsilon V \log \log \lvert d\rvert $
. After application of Lemma 6.4 and Stirling’s formula, the right-hand side is
$\ell \le \frac 13 \epsilon V \log \log \lvert d\rvert $
. After application of Lemma 6.4 and Stirling’s formula, the right-hand side is
 $ \ll _{\pi ,\epsilon } \lvert \operatorname {Cl}_K\rvert \left (\frac {2\ell \log \log \lvert d\rvert \left (1+\epsilon ^3\right )}{V_1^2 e} \right )^{\ell }. $
For
$ \ll _{\pi ,\epsilon } \lvert \operatorname {Cl}_K\rvert \left (\frac {2\ell \log \log \lvert d\rvert \left (1+\epsilon ^3\right )}{V_1^2 e} \right )^{\ell }. $
For
 $V \le \frac 13 \epsilon (\log \log \lvert d\rvert )^2$
, set
$V \le \frac 13 \epsilon (\log \log \lvert d\rvert )^2$
, set
 $\ell =\left \lfloor \frac {V_1^2}{2\log \log \lvert d\rvert } \right \rfloor $
, and for larger V, take
$\ell =\left \lfloor \frac {V_1^2}{2\log \log \lvert d\rvert } \right \rfloor $
, and for larger V, take
![]() $\ell = \lfloor \epsilon V/3 \rfloor $
. Hence
$\ell = \lfloor \epsilon V/3 \rfloor $
. Hence
 $$ \begin{align} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \left\lvert\left\{ \Lambda \in \widehat{\operatorname{Cl}_K}: P_1(\Lambda)> V_1 \right\}\right\rvert \ll_{\pi, \epsilon} \exp\left(\frac{-V^2(1-2\epsilon)}{2 \log \log \lvert d\rvert}\right)+e^{-\frac{\epsilon}{4} V \log V}. \end{align} $$
$$ \begin{align} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \left\lvert\left\{ \Lambda \in \widehat{\operatorname{Cl}_K}: P_1(\Lambda)> V_1 \right\}\right\rvert \ll_{\pi, \epsilon} \exp\left(\frac{-V^2(1-2\epsilon)}{2 \log \log \lvert d\rvert}\right)+e^{-\frac{\epsilon}{4} V \log V}. \end{align} $$
Arguing as before, taking
![]() $\ell =\lfloor \epsilon V/3\rfloor $
, and using the bound
$\ell =\lfloor \epsilon V/3\rfloor $
, and using the bound
![]() $\lvert a_{\pi }(p)\rvert ^2 \le 16$
, we have
$\lvert a_{\pi }(p)\rvert ^2 \le 16$
, we have
 $$ \begin{align} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \left\lvert\left\{ \Lambda \in \widehat{\operatorname{Cl}}_K: P_2(\Lambda)> V_2 \right\}\right\rvert & \ll \frac{(2\ell)!}{\left(V_2^22\right)^{\ell} \ell!} \left( 2 \sum_{\substack{z \le p \le x \\ p \nmid N }} \frac{a_{\pi}(p)^2}{p} \right)^{\ell} \nonumber\\ & \ll \left( \frac{65 \ell \log \log \log \lvert d\rvert}{V_2^2 } \right)^{\ell} \ll_{\epsilon} e^{-\frac{\epsilon}{4}V \log V}. \end{align} $$
$$ \begin{align} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \left\lvert\left\{ \Lambda \in \widehat{\operatorname{Cl}}_K: P_2(\Lambda)> V_2 \right\}\right\rvert & \ll \frac{(2\ell)!}{\left(V_2^22\right)^{\ell} \ell!} \left( 2 \sum_{\substack{z \le p \le x \\ p \nmid N }} \frac{a_{\pi}(p)^2}{p} \right)^{\ell} \nonumber\\ & \ll \left( \frac{65 \ell \log \log \log \lvert d\rvert}{V_2^2 } \right)^{\ell} \ll_{\epsilon} e^{-\frac{\epsilon}{4}V \log V}. \end{align} $$
Similarly,
 $$ \begin{align} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \left\lvert\left\{ \Lambda \in \widehat{\operatorname{Cl}_K}: P_3(\Lambda)> V_2 \right\}\right\rvert \ll \frac{(2\ell)!}{\left(V_2^22\right)^{\ell} \ell!} \left( \sum_{\substack{p\mid d, p \nmid N}} \frac{a_{\pi}(p)^2}{p} \right)^{\ell} \ll_{\epsilon} e^{-\frac{\epsilon}{4}V \log V}. \end{align} $$
$$ \begin{align} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \left\lvert\left\{ \Lambda \in \widehat{\operatorname{Cl}_K}: P_3(\Lambda)> V_2 \right\}\right\rvert \ll \frac{(2\ell)!}{\left(V_2^22\right)^{\ell} \ell!} \left( \sum_{\substack{p\mid d, p \nmid N}} \frac{a_{\pi}(p)^2}{p} \right)^{\ell} \ll_{\epsilon} e^{-\frac{\epsilon}{4}V \log V}. \end{align} $$
6.5. Proof of Theorem 6.1
Let
 $ B_K(V)=\frac {1}{\lvert \operatorname {Cl}_K\rvert } \left \lvert \left \{ \Lambda \in \widehat {\operatorname {Cl}}_K : \log L\left (\tfrac 12, \pi \times {\mathcal {AI}}(\Lambda )\right )> V \right \}\right \rvert. $
Observe that
$ B_K(V)=\frac {1}{\lvert \operatorname {Cl}_K\rvert } \left \lvert \left \{ \Lambda \in \widehat {\operatorname {Cl}}_K : \log L\left (\tfrac 12, \pi \times {\mathcal {AI}}(\Lambda )\right )> V \right \}\right \rvert. $
Observe that
 $$ \begin{align} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{\operatorname{Cl}_K} } \sqrt{L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right)}&=\frac12 \int_{\mathbb R} e^{V/2} B_K(V) dV\nonumber\\ &= \frac{1}{2 (\log \lvert d\rvert)^{1/4}} \int_{\mathbb R} e^{V/2} B_K\left(V-\tfrac12 \log \log \lvert d\rvert\right) dV. \end{align} $$
$$ \begin{align} \frac{1}{\lvert\operatorname{Cl}_K\rvert} \sum_{\Lambda \in \widehat{\operatorname{Cl}_K} } \sqrt{L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right)}&=\frac12 \int_{\mathbb R} e^{V/2} B_K(V) dV\nonumber\\ &= \frac{1}{2 (\log \lvert d\rvert)^{1/4}} \int_{\mathbb R} e^{V/2} B_K\left(V-\tfrac12 \log \log \lvert d\rvert\right) dV. \end{align} $$
It suffices to consider
 $2(\log \log \lvert d\rvert )^{3/4} \le V \le 2 C_0 \frac {\log \lvert d\rvert }{\log \log \lvert d\rvert }$
, as the contribution of
$2(\log \log \lvert d\rvert )^{3/4} \le V \le 2 C_0 \frac {\log \lvert d\rvert }{\log \log \lvert d\rvert }$
, as the contribution of
![]() $V \le 2(\log \log \lvert d\rvert )^{3/4}$
is trivially
$V \le 2(\log \log \lvert d\rvert )^{3/4}$
is trivially
 $O_{\varepsilon }\left ((\log \lvert d\rvert )^{-1/4+\varepsilon }\right )$
, and by Remark 6.3 we have
$O_{\varepsilon }\left ((\log \lvert d\rvert )^{-1/4+\varepsilon }\right )$
, and by Remark 6.3 we have
![]() $B_K(V)=0$
for
$B_K(V)=0$
for
 $V \ge 2 C_0 \frac {\log \lvert d\rvert }{\log \log \lvert d\rvert }$
.
$V \ge 2 C_0 \frac {\log \lvert d\rvert }{\log \log \lvert d\rvert }$
.
By Lemmas 6.2 and 6.4 and the bound (59), we have for
![]() $x \le \lvert d\rvert $
that
$x \le \lvert d\rvert $
that
 $$ \begin{align} \log L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right) \le P(\Lambda;x)-\tfrac12 \log \log \lvert d\rvert+2C_0\frac{ \log \lvert d\rvert}{\log x}+o( \log \log \lvert d\rvert). \end{align} $$
$$ \begin{align} \log L\left(\tfrac12, \pi \times {\mathcal{AI}}(\Lambda)\right) \le P(\Lambda;x)-\tfrac12 \log \log \lvert d\rvert+2C_0\frac{ \log \lvert d\rvert}{\log x}+o( \log \log \lvert d\rvert). \end{align} $$
Taking
 $x=\lvert d\vert ^{\frac {1}{\epsilon V}}$
, it follows from the bound (68) that
$x=\lvert d\vert ^{\frac {1}{\epsilon V}}$
, it follows from the bound (68) that
 $ B_K\left (V-\tfrac 12 \log \log \lvert d\rvert \right ) \le A_K\left (V(1-3C_0\epsilon ); \lvert d\rvert ^{\frac {1}{\epsilon V}}\right ). $
Applying the foregoing estimate and using Lemma 6.7 along with the identity
$ B_K\left (V-\tfrac 12 \log \log \lvert d\rvert \right ) \le A_K\left (V(1-3C_0\epsilon ); \lvert d\rvert ^{\frac {1}{\epsilon V}}\right ). $
Applying the foregoing estimate and using Lemma 6.7 along with the identity
 $$ \begin{align*} \int_{\mathbb R} e^{\frac{-t^2}{2 \log \log \lvert d\rvert}+t/2} dt = \sqrt{2\pi \log \log \lvert d\rvert} (\log \lvert d\rvert)^{\frac18}, \end{align*} $$
$$ \begin{align*} \int_{\mathbb R} e^{\frac{-t^2}{2 \log \log \lvert d\rvert}+t/2} dt = \sqrt{2\pi \log \log \lvert d\rvert} (\log \lvert d\rvert)^{\frac18}, \end{align*} $$
we get that the right-hand side of equation (67) is
 $$ \begin{align*} &\ll (\log \lvert d\rvert)^{-\frac14} \int_{2(\log \log \lvert d\rvert)^{3/4}}^{2C_0 \frac{\log \lvert d\rvert}{\log \log \lvert d\rvert}} \left( e^{\frac{-V^2\left(1-7C_0 \varepsilon\right)}{2\log \log \lvert d\rvert}} + e^{-\frac{\epsilon}{5}V \log V} \right) dV \\ & \quad + (\log \lvert d\rvert)^{-\frac14+\varepsilon} \ll_{\pi,\varepsilon} \frac{1}{(\log \lvert d\rvert)^{\frac18-\varepsilon}}, \end{align*} $$
$$ \begin{align*} &\ll (\log \lvert d\rvert)^{-\frac14} \int_{2(\log \log \lvert d\rvert)^{3/4}}^{2C_0 \frac{\log \lvert d\rvert}{\log \log \lvert d\rvert}} \left( e^{\frac{-V^2\left(1-7C_0 \varepsilon\right)}{2\log \log \lvert d\rvert}} + e^{-\frac{\epsilon}{5}V \log V} \right) dV \\ & \quad + (\log \lvert d\rvert)^{-\frac14+\varepsilon} \ll_{\pi,\varepsilon} \frac{1}{(\log \lvert d\rvert)^{\frac18-\varepsilon}}, \end{align*} $$
which completes the proof. □
Acknowledgments
We thank Ralf Schmidt for helpful discussions concerning the material in §5.4. We thank Valentin Blomer and Farrell Brumley for forwarding us their preprint [Reference Böcherer and Das5]. We thank the anonymous referee for useful comments and corrections which improved this paper. This work was supported by the Engineering and Physical Sciences Research Council (grant EP/T028343/1).
Competing Interest
The author(s) declare none.