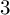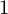Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shankhadhar, Karam Deo
and
Tiwari, Prashant
2023.
On sign changes of primitive Fourier coefficients of Siegel cusp forms.
Functiones et Approximatio Commentarii Mathematici,
Vol. 68,
Issue. 2,
Jääsaari, Jesse
Lester, Stephen
and
Saha, Abhishek
2023.
ON FUNDAMENTAL FOURIER COEFFICIENTS OF SIEGEL CUSP FORMS OF DEGREE 2.
Journal of the Institute of Mathematics of Jussieu,
Vol. 22,
Issue. 4,
p.
1819.
Anamby, Pramath
2024.
Non-vanishing of theta components of Jacobi forms with level and an application.
International Journal of Number Theory,
Vol. 20,
Issue. 02,
p.
549.
Martin, Yves
2025.
On prime numbers and quadratic forms represented by positive-definite, primitive quadratic forms.
Journal of Number Theory,
Vol. 274,
Issue. ,
p.
26.