Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T15:40:57.622Z Has data issue: false hasContentIssue false
  • English
  • Français

ON FUNDAMENTAL GROUPS OF TENSOR PRODUCT 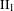$\text{II}_{1}$ FACTORS

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  02 August 2018

Yusuke Isono
Yusuke Isono*
Affiliation:
Research Institute for Mathematical Sciences, Kyoto University, 606-8502, Kyoto, Japan (isono@kurims.kyoto-u.ac.jp)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 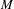$M$ be a 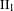$\text{II}_{1}$ factor and let 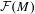${\mathcal{F}}(M)$ denote the fundamental group of 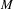$M$. In this article, we study the following property of 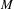$M$: for any 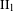$\text{II}_{1}$ factor 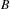$B$, we have 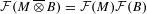${\mathcal{F}}(M\,\overline{\otimes }\,B)={\mathcal{F}}(M){\mathcal{F}}(B)$. We prove that for any subgroup $G\leqslant \mathbb{R}_{+}^{\ast }$ which is realized as a fundamental group of a 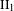$\text{II}_{1}$ factor, there exists a 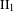$\text{II}_{1}$ factor 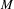$M$ which satisfies this property and whose fundamental group is 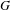$G$. Using this, we deduce that if 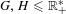$G,H\leqslant \mathbb{R}_{+}^{\ast }$ are realized as fundamental groups of 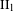$\text{II}_{1}$ factors, then so are groups 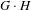$G\cdot H$ and 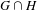$G\cap H$.

Keywords

functional analysisvon Neumann algebrasfundamental groups for II1 factors

MSC classification

Primary: 46L10: General theory of von Neumann algebras 46L36: Classification of factors
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 4 , July 2020 , pp. 1121 - 1139
Check for updates
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brown, N. P. and Ozawa, N., C ∗ -algebras and Finite-dimensional Approximations, Graduate Studies in Mathematics, Volume 88 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Chifan, I., Kida, Y. and Pant, S., Primeness results for von Neumann algebras associated with surface braid groups, Int. Math. Res. Not. IMRN 2016(16) (2015), 4807–4848.10.1093/imrn/rnv271Google Scholar
Chifan, I., Sinclair, T. and Udrea, B., On the structural theory of II1 factors of negatively curved groups, II. Actions by product groups, Adv. Math. 245 (2013), 208–236.10.1016/j.aim.2013.06.017Google Scholar
Connes, A., Classification of injective factors. Cases II1 , II∞, III𝜆 , 𝜆≠1, Ann. of Math. (2) 104 (1976), 73–115.10.2307/1971057Google Scholar
Connes, A., A factor of type II1 with countable fundamental group, J. Operator Theory 4 (1980), 151–153.Google Scholar
Deprez, S., Explicit examples of equivalence relations and factors with prescribed fundamental group and outer automorphism group, preprint, 2010, arXiv:1010.3612.Google Scholar
Dykema, K. J. and Rădulescu, F., Compressions of free products of von Neumann algebras, Math. Ann. 316 (2000), 61–82.10.1007/s002080050004Google Scholar
Gaboriau, D., Coût des relations d’équivalence et des groupes, Invent. Math. 139(1) (2000), 41–98.10.1007/s002229900019Google Scholar
Gaboriau, D., Invariants ℓ 2 de relations d’équivalence et de groupes, Publ. Math. Inst. Hautes Études Sci. 95 (2002), 93–150.10.1007/s102400200002Google Scholar
Hoff, D. J., Von Neumann algebras of equivalence relations with nontrivial one-cohomology, J. Funct. Anal. 270(4) (2016), 1501–1536.10.1016/j.jfa.2015.10.006Google Scholar
Houdayer, C., Construction of type II1 factors with prescribed countable fundamental group, J. Reine Angew Math. 634 (2009), 169–207.Google Scholar
Houdayer, C. and Isono, Y., Unique prime factorization and bicentralizer problem for a class of type III factors, Adv. Math. 305 (2017), 402–455.10.1016/j.aim.2016.09.030Google Scholar
Houdayer, C. and Ueda, Y., Rigidity of free product von Neumann algebras, Compos. Math. 152 (2016), 2461–2492.10.1112/S0010437X16007673Google Scholar
Ioana, A., Cartan subalgebras of amalgamated free product II1 factors (with an appendix joint with S. Vaes), Ann. Sci. Éc. Norm. Supér. 48 (2015), 71–130.10.24033/asens.2239Google Scholar
Ioana, A., Peterson, J. and Popa, S., Amalgamated free products of weakly rigid factors and calculation of their symmetry groups, Acta Math. 200 (2008), 85–153.10.1007/s11511-008-0024-5Google Scholar
Isono, Y., Weak Exactness for C∗ -algebras and Application to Condition (AO), J. Funct. Anal. 264 (2013), 964–998.10.1016/j.jfa.2012.10.021Google Scholar
Isono, Y., Some prime factorization results for free quantum group factors, J. Reine Angew. Math. 722 (2017), 215–250.Google Scholar
Murray, F. J. and Von Neumann, J., On rings of operators IV, Ann. of Math. (2) 44 (1943), 716–808.10.2307/1969107Google Scholar
Ozawa, N., A Kurosh type theorem for type II1 factors, Int. Math. Res. Not. IMRN (2006), Art. ID 97560, 21 pp.10.1155/IMRN/2006/97560Google Scholar
Ozawa, N., An example of a solid von Neumann algebra, Hokkaido Math. J. 38 (2009), 557–561.10.14492/hokmj/1258553976Google Scholar
Ozawa, N. and Popa, S., Some prime factorization results for type II1 factors, Invent. Math. 156 (2004), 223–234.10.1007/s00222-003-0338-zGoogle Scholar
Ozawa, N. and Popa, S., On a class of II1 factors with at most one Cartan subalgebra, Ann. of Math. (2) 172 (2010), 713–749.10.4007/annals.2010.172.713Google Scholar
Peterson, J., L2 -rigidity in von Neumann algebras, Invent. Math. 175 (2009), 417–433.10.1007/s00222-008-0154-6Google Scholar
Popa, S., On a class of type II1 factors with Betti numbers invariants, Ann. of Math. (2) 163 (2006), 809–899.10.4007/annals.2006.163.809Google Scholar
Popa, S., Strong rigidity of II1 factors arising from malleable actions of w-rigid groups I, Invent. Math. 165 (2006), 369–408.10.1007/s00222-006-0501-4Google Scholar
Popa, S., Strong rigidity of II1 factors arising from malleable actions of w-rigid groups, II, Invent. Math. 165 (2006), 409–452.10.1007/s00222-006-0502-3Google Scholar
Popa, S., On the superrigidity of malleable actions with spectral gap, J. Amer. Math. Soc. 21 (2008), 981–1000.10.1090/S0894-0347-07-00578-4Google Scholar
Popa, S., On Ozawa’s property for free group factors, Int. Math. Res. Not. IMRN 2007(11) (2007), Art. ID rnm036, 10 pp.Google Scholar
Popa, S. and Vaes, S., Actions of 𝔽∞ whose II1 factors and orbit equivalence relations have prescribed fundamental group, J. Amer. Math. Soc. 23 (2010), 383–403.Google Scholar
Popa, S. and Vaes, S., On the fundamental group of II1 factors and equivalence relations arising from group actions, in Quanta of Maths, Proceedings of the Conference in honor of A. Connes’ 60th birthday, Clay Mathematics Institute Proceedings, Volume 11, pp. 519–541 (Amer. Math. Soc., Providence, RI, 2010).Google Scholar
Popa, S. and Vaes, S., Unique Cartan decomposition for II1 factors arising from arbitrary actions of hyperbolic groups, J. Reine Angew. Math. 694 (2014), 215–239.Google Scholar
Rădulescu, F., The fundamental group of the von Neumann algebra of a free group with infinitely many generators is ℝ+∗, J. Amer. Math. Soc. 5 (1992), 517–532.Google Scholar
Sako, H., Measure equivalence rigidity and bi-exactness of groups, J. Funct. Anal. 257 (2009), 3167–3202.Google Scholar
Sizemore, J. O. and Winchester, A., A unique prime decomposition result for wreath product factors, Pacific J. Math. 265(1) (2013), 221–232.Google Scholar
Vaes, S., Explicit computations of all finite index bimodules for a family of II1 factors, Ann. Sci. Éc. Norm. Supér. 41 (2008), 743–788.Google Scholar
Vaes, S., Normalizers inside amalgamated free product von Neumann algebras, Publ. Res. Inst. Math. Sci. 50 (2014), 695–721.Google Scholar
Voiculescu, D. V., Circular and semicircular systems and free product factors, in Operator Algebras, Unitary Representations, Enveloping Algebras, and Invariant Theory (Paris, 1989), Progr. Math., Volume 92, pp. 45–60 (Birkhäuser, Boston, 1990).Google Scholar