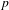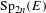Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mitra, Arnab
2019.
On the relationship between distinction and irreducibility of parabolic induction.
Comptes Rendus. Mathématique,
Vol. 357,
Issue. 11-12,
p.
827.
Dijols, Sarah
2025.
Parabolically Induced Representations of
p
-adic
G
2
Distinguished by SO
4
, I
.
Experimental Mathematics,
p.
1.