Hostname: page-component-7dd5485656-jtdwj Total loading time: 0 Render date: 2025-10-30T03:59:48.794Z Has data issue: false hasContentIssue false
  • English
  • Français

On the cubic NLS on 3D compact domains

Published online by Cambridge University Press:  04 February 2013

Fabrice Planchon
Fabrice Planchon*
Affiliation:
Laboratoire J. A. Dieudonné, UMR 7351, Université de Nice Sophia-Antipolis, Parc Valrose, F-06108 Nice Cedex 02, et Institut universitaire de France (fabrice.planchon@unice.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove bilinear estimates for the Schrödinger equation on 3D domains, with Dirichlet boundary conditions. On non-trapping domains, they match the 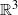${ \mathbb{R} }^{3} $ case, while on bounded domains they match the generic boundaryless manifold case. We obtain, as an application, global well-posedness for the defocusing cubic NLS for data in 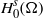${ H}_{0}^{s} (\Omega )$, 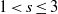$1\lt s\leq 3$, with 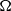$\Omega $ any bounded domain with smooth boundary.

Résumé

On démontre des estimations bilinéaires pour l’équation de Schrödinger sur des domaines tridimensionnels, avec condition de Dirichlet au bord. Dans le cas non-captant, on retrouve les estimations connues dans 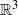${ \mathbb{R} }^{3} $, et sur un domaine borné on obtient des estimations similaires à celles du cas d’une variété compacte générique sans bord. Une application est donnée à l’existence de solutions globales dans 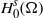${ H}_{0}^{s} (\Omega )$, 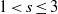$1\lt s\leq 3$, avec 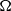$\Omega $ un domaine borné régulier.

Keywords

35-xx partial differential equations

Information

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 13 , Issue 1 , January 2014 , pp. 1 - 18
Copyright
©Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Anton, Ramona, Cubic nonlinear Schrödinger equation on three dimensional balls with radial data, Comm. Partial Differential Equations 33 (10–12) (2008), 1862–1889.Google Scholar
Anton, Ramona, Strichartz inequalities for Lipschitz metrics on manifolds and nonlinear Schrödinger equation on domains, Bull. Soc. Math. France 136 (1) (2008), 27–65.Google Scholar
Blair, M. D., Smith, H. F. and Sogge, C. D., Strichartz estimates and the nonlinear Schrödinger equation on manifolds with boundary, Math. Ann. 354 (4) (2012), 1397–1430.Google Scholar
Blair, Matthew D., Smith, Hart F. and Sogge, Christopher D., On Strichartz estimates for Schrödinger operators in compact manifolds with boundary, Proc. Amer. Math. Soc. 136 (1) (2008), 247–256 (electronic).Google Scholar
Bourgain, J., Exponential sums and nonlinear Schrödinger equations, Geom. Funct. Anal. 3 (2) (1993), 157–178.Google Scholar
Bourgain, J., Fourier transform restriction phenomena for certain lattice subsets and applications to nonlinear evolution equations. I. Schrödinger equations, Geom. Funct. Anal. 3 (2) (1993), 107–156.Google Scholar
Bourgain, J., Refinements of Strichartz’ inequality and applications to 2D-NLS with critical nonlinearity, Internat. Math. Res. Not. (5) (1998), 253–283.CrossRefGoogle Scholar
Burq, N., Smoothing effect for Schrödinger boundary value problems, Duke Math. J. 123 (2) (2004), 403–427.Google Scholar
Burq, N., Gérard, P. and Tzvetkov, N., On nonlinear Schrödinger equations in exterior domains, Ann. Inst. H. Poincaré Anal. Non Linéaire 21 (3) (2004), 295–318.Google Scholar
Burq, N., Gérard, P. and Tzvetkov, N., Strichartz inequalities and the nonlinear Schrödinger equation on compact manifolds, Amer. J. Math. 126 (3) (2004), 569–605.CrossRefGoogle Scholar
Burq, N., Gérard, P. and Tzvetkov, N., Bilinear eigenfunction estimates and the nonlinear Schrödinger equation on surfaces, Invent. Math. 159 (1) (2005), 187–223.Google Scholar
Burq, Nicolas, Gérard, Patrick and Tzvetkov, Nikolay, Multilinear eigenfunction estimates and global existence for the three dimensional nonlinear Schrödinger equations, Ann. Sci. Éc. Norm. Super. (4) 38 (2) (2005), 255–301.CrossRefGoogle Scholar
Cazenave, Thierry and Weissler, Fred B., The Cauchy problem for the critical nonlinear Schrödinger equation in ${H}^{s} $, Nonlinear Anal. 14 (10) (1990), 807–836.Google Scholar
Colliander, J., Keel, M., Staffilani, G., Takaoka, H. and Tao, T., Global well-posedness and scattering for the energy-critical nonlinear Schrödinger equation in ${ \mathbb{R} }^{3} $, Ann. of Math. (2) 167 (3) (2008), 767–865.Google Scholar
Dodson, B., Global well-posedness and scattering for the defocusing, energy-critical, nonlinear Schrödinger equation in the exterior of a convex obstacle when $d= 4$ (arXiv:math/1112.0710), December 2011.Google Scholar
Ginibre, J. and Velo, G., Scattering theory in the energy space for a class of nonlinear Schrödinger equations, J. Math. Pures Appl. (9) 64 (4) (1985), 363–401.Google Scholar
Hadac, Martin, Herr, Sebastian and Koch, Herbert, Well-posedness and scattering for the KP-II equation in a critical space, Ann. Inst. H. Poincaré Anal. Non Linéaire 26 (3) (2009), 917–941.Google Scholar
Hani, Z., A bilinear oscillatory integral estimate and bilinear refinements to Strichartz estimates on closed manifolds, Anal. PDE 5 (2) (2012), 339–363.Google Scholar
Ivanovici, Oana, Counterexamples to Strichartz estimates for the wave equation in domains, Math. Ann. 347 (3) (2010), 627–673.Google Scholar
Ivanovici, Oana, On the Schrödinger equation outside strictly convex obstacles, Anal. PDE 3 (3) (2010), 261–293.Google Scholar
Ivanovici, Oana and Planchon, Fabrice, Square function and heat flow estimates on domains (arXiv:math/0812.2733), 2008.Google Scholar
Ivanovici, Oana and Planchon, Fabrice, On the energy critical Schrödinger equation in 3D non-trapping domains, Ann. Inst. H. Poincaré Anal. Non Linéaire 27 (5) (2010), 1153–1177.Google Scholar
Keel, Markus and Tao, Terence, Endpoint Strichartz estimates, Amer. J. Math. 120 (5) (1998), 955–980.Google Scholar
Koch, Herbert and Tataru, Daniel, Dispersive estimates for principally normal pseudodifferential operators, Comm. Pure Appl. Math. 58 (2) (2005), 217–284.Google Scholar
Koch, Herbert and Tataru, Daniel, A priori bounds for the 1D cubic NLS in negative Sobolev spaces, Int. Math. Res. Not. IMRN 16 (2007), 36, Art. ID rnm053.Google Scholar
Pausader, Benoit, Tzvetkov, Nikolay and Wang, Xuecheng, Global regularity for the energy-critical NLS on ${ \mathbb{S} }^{3} $, 2012 (arXiv:math/1210.3842).Google Scholar
Planchon, Fabrice, Existence globale et scattering pour les solutions de masse finie de l’équation de Schrödinger cubique en dimension deux (d’après Benjamin Dodson, Rowan Killip, Terence Tao, Monica Vişan et Xiaoyi Zhang), Astérisque. Exp. No. 1042, Séminaire Bourbaki. Volume 2010/2011.Google Scholar
Planchon, Fabrice and Vega, Luis, Bilinear virial identities and applications, Ann. Scient. Éc. Norm. Super. 42 (2009), 261–290.Google Scholar
Smith, P., Conditional global regularity of Schrödinger maps: sub-threshold dispersed energy (arXiv:math/1012.4048), December 2010.Google Scholar
Smith, P., Global regularity of critical Schrödinger maps: subthreshold dispersed energy (arXiv:math/1112.0251), December 2011.Google Scholar
Staffilani, Gigliola and Tataru, Daniel, Strichartz estimates for a Schrödinger operator with nonsmooth coefficients, Comm. Partial Differential Equations 27 (7–8) (2002), 1337–1372.CrossRefGoogle Scholar
Strichartz, Robert S., Restrictions of Fourier transforms to quadratic surfaces and decay of solutions of wave equations, Duke Math. J. 44 (3) (1977), 705–714.CrossRefGoogle Scholar