Article contents
ON THE GROWTH OF TORSION IN THE COHOMOLOGY OF ARITHMETIC GROUPS
Published online by Cambridge University Press: 21 March 2018
Abstract
Let 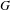 $G$ be a semisimple Lie group with associated symmetric space
$G$ be a semisimple Lie group with associated symmetric space 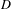 $D$, and let
$D$, and let 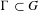 $\unicode[STIX]{x1D6E4}\subset G$ be a cocompact arithmetic group. Let
$\unicode[STIX]{x1D6E4}\subset G$ be a cocompact arithmetic group. Let 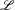 $\mathscr{L}$ be a lattice inside a
$\mathscr{L}$ be a lattice inside a  $\mathbb{Z}\unicode[STIX]{x1D6E4}$-module arising from a rational finite-dimensional complex representation of
$\mathbb{Z}\unicode[STIX]{x1D6E4}$-module arising from a rational finite-dimensional complex representation of 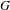 $G$. Bergeron and Venkatesh recently gave a precise conjecture about the growth of the order of the torsion subgroup
$G$. Bergeron and Venkatesh recently gave a precise conjecture about the growth of the order of the torsion subgroup 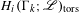 $H_{i}(\unicode[STIX]{x1D6E4}_{k};\mathscr{L})_{\operatorname{tors}}$ as
$H_{i}(\unicode[STIX]{x1D6E4}_{k};\mathscr{L})_{\operatorname{tors}}$ as 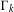 $\unicode[STIX]{x1D6E4}_{k}$ ranges over a tower of congruence subgroups of
$\unicode[STIX]{x1D6E4}_{k}$ ranges over a tower of congruence subgroups of 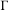 $\unicode[STIX]{x1D6E4}$. In particular, they conjectured that the ratio
$\unicode[STIX]{x1D6E4}$. In particular, they conjectured that the ratio 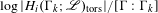 $\log |H_{i}(\unicode[STIX]{x1D6E4}_{k};\mathscr{L})_{\operatorname{tors}}|/[\unicode[STIX]{x1D6E4}:\unicode[STIX]{x1D6E4}_{k}]$ should tend to a nonzero limit if and only if
$\log |H_{i}(\unicode[STIX]{x1D6E4}_{k};\mathscr{L})_{\operatorname{tors}}|/[\unicode[STIX]{x1D6E4}:\unicode[STIX]{x1D6E4}_{k}]$ should tend to a nonzero limit if and only if 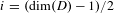 $i=(\dim (D)-1)/2$ and
$i=(\dim (D)-1)/2$ and 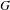 $G$ is a group of deficiency
$G$ is a group of deficiency  $1$. Furthermore, they gave a precise expression for the limit. In this paper, we investigate computationally the cohomology of several (non-cocompact) arithmetic groups, including
$1$. Furthermore, they gave a precise expression for the limit. In this paper, we investigate computationally the cohomology of several (non-cocompact) arithmetic groups, including 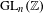 $\operatorname{GL}_{n}(\mathbb{Z})$ for
$\operatorname{GL}_{n}(\mathbb{Z})$ for 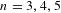 $n=3,4,5$ and
$n=3,4,5$ and 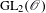 $\operatorname{GL}_{2}(\mathscr{O})$ for various rings of integers, and observe its growth as a function of level. In all cases where our dataset is sufficiently large, we observe excellent agreement with the same limit as in the predictions of Bergeron–Venkatesh. Our data also prompts us to make two new conjectures on the growth of torsion not covered by the Bergeron–Venkatesh conjecture.
$\operatorname{GL}_{2}(\mathscr{O})$ for various rings of integers, and observe its growth as a function of level. In all cases where our dataset is sufficiently large, we observe excellent agreement with the same limit as in the predictions of Bergeron–Venkatesh. Our data also prompts us to make two new conjectures on the growth of torsion not covered by the Bergeron–Venkatesh conjecture.
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 2 , March 2020 , pp. 537 - 569
- Copyright
- © Cambridge University Press 2018
Footnotes
The authors thank the Banff International Research Station and Wesleyan University, where some work was carried out on this paper. A. A. was partially supported by NSA grant H98230-09-1-0050. P. G. was partially supported by NSF grants DMS 1101640 and 1501832. D. Y. was partially supported by NSA grant H98230-15-1-0228. This manuscript is submitted for publication with the understanding that the United States government is authorized to produce and distribute reprints.
References
- 3
- Cited by

