Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T20:00:45.031Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE SUBSTITUTION THEOREM FOR RINGS OF SEMIALGEBRAIC FUNCTIONS

Part of: Real and complex fields Maps and general types of spaces defined by maps Chain conditions, finiteness conditions

Published online by Cambridge University Press:  01 July 2014

José F. Fernando
José F. Fernando*
Affiliation:
Departamento de Álgebra, Facultad de Ciencias Matemáticas, Universidad Complutense de Madrid, 28040 Madrid, Spain (josefer@mat.ucm.es)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 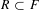$R\subset F$ be an extension of real closed fields, and let 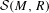${\mathcal{S}}(M,R)$ be the ring of (continuous) semialgebraic functions on a semialgebraic set 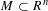$M\subset R^{n}$. We prove that every 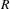$R$-homomorphism 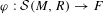${\it\varphi}:{\mathcal{S}}(M,R)\rightarrow F$ is essentially the evaluation homomorphism at a certain point 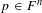$p\in F^{n}$ adjacent to the extended semialgebraic set 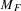$M_{F}$. This type of result is commonly known in real algebra as a substitution lemma. In the case when 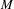$M$ is locally closed, the results are neat, while the non-locally closed case requires a more subtle approach and some constructions (weak continuous extension theorem, appropriate immersion of semialgebraic sets) that have interest of their own. We consider the same problem for the ring of bounded (continuous) semialgebraic functions, getting results of a different nature.

Keywords

semialgebraic setring of semialgebraic functionsextension of coefficientsevaluation homomorphismssubstitution theoremweak continuous extension property

MSC classification

Primary: 14P10: Semialgebraic sets and related spaces 54C30: Real-valued functions
Secondary: 12D15: Fields related with sums of squares (formally real fields, Pythagorean fields, etc.) 13E99: None of the above, but in this section
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 14 , Issue 4 , October 2015 , pp. 857 - 894
Copyright
© Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berger, M., Geometry I. Universitext. Springer-Verlag, Berlin: 1987.Google Scholar
Biström, P. and Lindström, M., Homomorphisms on C∞(E) and C∞ -bounding sets, Monatsh. Math. 115(3) (1993), 257–266.Google Scholar
Bochnak, J., Coste, M. and Roy, M.-F., Real algebraic geometry, in Ergeb. Math., Volume 36 (Springer-Verlag, Berlin, 1998).Google Scholar
Carral, M. and Coste, M. , Normal spectral spaces and their dimensions, J. Pure Appl. Algebra 30 (1983), 227–235.Google Scholar
Cherlin, G. L. and Dickmann, M. A. , Real closed rings I. Residue rings of rings of continuous functions, Fund. Math. 126(2) (1986), 147–183.CrossRefGoogle Scholar
Cherlin, G. L. and Dickmann, M. A. , Real closed rings II. Model theory, Ann. Pure Appl. Logic 25(3) (1983), 213–231.Google Scholar
Delfs, H. and Knebusch, M., On the homology of algebraic varieties over real closed fields, J. Reine Angew. Math. 335 (1982), 122–163.Google Scholar
Delfs, H. and Knebusch, M., Separation, retractions and homotopy extension in semialgebraic spaces, Pacific J. Math. 114(1) (1984), 47–71.CrossRefGoogle Scholar
Delfs, H. and Knebusch, M., Locally semialgebraic spaces, in Lecture Notes in Mathematics, Volume 1173 (Springer-Verlag, Berlin, 1985).Google Scholar
Efroymson, G. A., Substitution in Nash functions, Pacific J. Math. 63(1) (1976), 137–145.Google Scholar
Fernando, J. F., On chains of prime ideals in rings of semialgebraic functions, Q. J. Math. (2013) (accepted); doi:10.1093/qmath/hat048.Google Scholar
Fernando, J. F. and Gamboa, J. M. , On the irreducible components of a semialgebraic set, Internat. J. Math. 23(4) (2012), 1250031, 40 pp.Google Scholar
Fernando, J. F. and Gamboa, J. M. , On the Krull dimension of rings of semialgebraic functions. Preprint RAAG (2013). arXiv:1306.4109.Google Scholar
Fernando, J. F., Gamboa, J. M. and Ruiz, J. M. , Finiteness problems on Nash manifolds and Nash sets, J. Eur. Math. Soc. (JEMS) 16(3) (2014), 537–570.CrossRefGoogle Scholar
Gómez, J. and Llavona, J. G., Multiplicative functionals on function algebras, Rev. Mat. Univ. Complut. Madrid 1(1–3) (1988), 19–22.Google Scholar
Jaramillo, J. A., Topologies and homomorphisms on algebras of differentiable functions, Math. Japon. 35(2) (1990), 343–349.Google Scholar
Kriegl, A., Michor, P. and Schachermayer, W., Characters on algebras of smooth functions, Ann. Global Anal. Geom. 7(2) (1989), 85–92.Google Scholar
Prestel, A. and Schwartz, N., Model theory of real closed rings. Valuation theory and its applications, Vol. I (Saskatoon, SK, 1999), 261–290, Fields Inst. Commun., 32, Amer. Math. Soc., Providence, RI, 2002.Google Scholar
Ruiz, J. M., A dimension theorem for real spectra, J. Algebra 124(2) (1989), 271–277.Google Scholar
Schwartz, N., Real closed rings. Habilitationsschrift, München: 1984.Google Scholar
Schwartz, N., Real closed rings. Algebra and order (Luminy–Marseille, 1984), 175–194, Res. Exp. Math., 14, Heldermann, Berlin: 1986.Google Scholar
Schwartz, N., The basic theory of real closed spaces, Mem. Amer. Math. Soc. 77(397) (1989).Google Scholar
Schwartz, N., Rings of continuous functions as real closed rings, in Ordered algebraic structures (Curaçao, 1995), pp. 277–313 (Kluwer Acad. Publ., Dordrecht, 1997).Google Scholar
Schwartz, N. and Madden, J. J., Semi-algebraic function rings and reflectors of partially ordered rings, in Lecture Notes in Mathematics, Volume 1712 (Springer-Verlag, Berlin, 1999).Google Scholar
Schwartz, N. and Tressl, M., Elementary properties of minimal and maximal points in Zariski spectra, J. Algebra 323(3) (2010), 698–728.CrossRefGoogle Scholar
Tressl, M., The real spectrum of continuous definable functions in o-minimal structures. Séminaire de Structures Algébriques Ordonnées 1997–1998, 68, Mars 1999, p. 1–15.Google Scholar
Tressl, M., Super real closed rings, Fund. Math. 194(2) (2007), 121–177.Google Scholar
Tressl, M., Bounded super real closed rings. Logic Colloquium 2007, 220–237, Lect. Notes Log., 35, Assoc. Symbol. Logic, La Jolla, CA, 2010.Google Scholar
Zame, W. R., Homomorphisms of rings of germs of analytic functions, Proc. Amer. Math. Soc. 33 (1972), 410–414.CrossRefGoogle Scholar