Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T19:41:34.010Z Has data issue: false hasContentIssue false
  • English
  • Français

Overconvergent Eichler–Shimura isomorphisms

Part of: Discontinuous groups and automorphic forms Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  02 January 2014

Fabrizio Andreatta ,
Adrian Iovita  and
Glenn Stevens
Fabrizio Andreatta
Affiliation:
Dipartimento di Matematica ‘Federigo Enriques’, Università degli Studi di Milano, Via C. Saldini 50, Milano 20133, Italia (fabrizio.andreatta@unimi.it)
Adrian Iovita
Affiliation:
Dipartimento di Matematica dell’Universita di Padova, via Trieste 63, Padova, Italia Department of Mathematics and Statistics, Concordia University, 1455 de Maisonneuve West Blvd., Montreal, QC, H3G 1M8, Canada (iovita@mathstat.concordia.ca)
Glenn Stevens
Affiliation:
Department of Mathematics and Statistics, Boston University, 111 Cummington Street, Boston, MA 02215, USA (ghs@math.bu.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

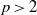Given a prime $p\gt 2$, an integer 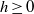$h\geq 0$, and a wide open disk 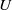$U$ in the weight space 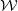$ \mathcal{W} $ of 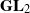${\mathbf{GL} }_{2} $, we construct a Hecke–Galois-equivariant morphism 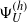${ \Psi }_{U}^{(h)} $ from the space of analytic families of overconvergent modular symbols over 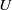$U$ with bounded slope 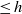$\leq h$, to the corresponding space of analytic families of overconvergent modular forms, all with 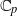${ \mathbb{C} }_{p} $-coefficients. We show that there is a finite subset 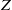$Z$ of 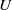$U$ for which this morphism induces a 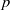$p$-adic analytic family of isomorphisms relating overconvergent modular symbols of weight 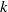$k$ and slope 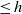$\leq h$ to overconvergent modular forms of weight 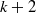$k+ 2$ and slope 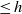$\leq h$.

Keywords

overconvergent modular symbols; overconvergent modular forms; p-adic comparison isomorphisms; Galois representations; Hodge–Tate decomposition

MSC classification

Secondary: 11F85: $p$-adic theory, local fields 14G20: Local ground fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 14 , Issue 2 , April 2015 , pp. 221 - 274
Copyright
©Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreatta, F. and Iovita, A., Erratum to the article Global applications to relative $(\varphi , \Gamma )$ -modules, I, in Représentations p-adiques de groupes p-adiques II: Représentations de GL 2( ℚp) et (φ,Γ)-modules, Astérisque, Volume 330, pp. 543–554 (Société de Mathématique de France, 2010).Google Scholar
Andreatta, F. and Iovita, A., Semi-stable sheaves and the comparison isomorphisms for semi-stable formal schemes, Rendiconti del Seminario Matematico dell’Università di Padova 128 (2012), 131–285.Google Scholar
Andreatta, F., Iovita, A. and Pilloni, V., $p$ -adic families of Siegel cuspforms, Ann. of Math., in press.Google Scholar
Andreatta, F., Iovita, A. and Stevens, G., Overconvergent modular sheaves and modular forms for ${\mathbf{GL} }_{2/ F} $ , Israel J. Math., in press.Google Scholar
Ash, A. and Stevens, G., p-adic deformations of arithmetic cohomology, preprint (available at http://math.bu.edu/people/ghs) (2008).Google Scholar
Coleman, R., $p$ -adic Banach spaces and families of modular forms, Invent. Math. 127 (1997), 417–479.Google Scholar
Deligne, P., Formes modulaires et représentations $\ell $ -adiques, Sem. Bourbaki, exp. 355 (1968-1969), 139–172.Google Scholar
Emerton, M., On the interpolation of systems of eigenvalues attached to automorphic Hecke eigenforms, Invent. Math. 164 (1) (2006), 1–84.Google Scholar
Faltings, G., Hodge–Tate structures of modular forms, Math. Ann. 278 (1987), 133–149.Google Scholar
Faltings, G., Almost étale extensions, in Cohomologies p-adiques et applications arithmétiques, vol. II (ed. Berthelot, P., Fontaine, J.-M., Illusie, L., Kato, K. and Rapoport, M.). Astérisque, Volume 279, pp. 185–270 (Société de Mathématique de France, 2002).Google Scholar
Harris, M., Iovita, A. and Stevens, G., A geometric Jacquet–Langlands corespondence, preprint (available at http://math.bu.edu/people/ghs) (2010).Google Scholar
Hyodo, O., On variation of Hodge–Tate structures, Math. Ann. 283 (1989), 7–22.Google Scholar
Illusie, L., An overview of the work of the work of K. Fujiwara, K. Kato and C. Nakamura on logarithmic étale cohomology, Astérisque, Volume 279, pp. 271–322 (Société de Mathématique de France, 2002).Google Scholar
Kato, K., Semi-stable reduction and $p$ -adic étale cohomology, in Périodes p-adiques (Bures-sur-Yvette, 1988), Astérisque, Volume 223, pp. 269–293 (Société de Mathématique de France, 1994).Google Scholar
Kato, K., Toric singularities, Amer. J. Math. 116 (1994), 1073–1099.CrossRefGoogle Scholar
Kisin, M., Overconvergent modular forms and the Fontaine–Mazur conjecture, Invent. Math. 153 (2003), 373–454.Google Scholar
Sen, S., The analytic variation of $p$ -adic Hodge Structures, Ann. Math. 127 (1988), 647–661.Google Scholar
Sen, S., An infinite dimensional Hodge–Tate theory, Bull. Soc. Math. France 121 (1993), 13–34.Google Scholar
Théorie des topos et cohomologie étale des schémas. Tome 1: Théorie des topos. Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4). Dirigé par M. Artin, A. Grothendieck, et J. L. Verdier. Avec la collaboration de N. Bourbaki, P. Deligne et B. Saint-Donat, Lecture Notes in Mathematics, Volume 269 (Springer, 1972).Google Scholar
Tate, J., $p$ -divisible groups, in Proc. Conf. Local Fields (Driebergen, 1966), pp. 158–183 (Société de Mathématique de France, 1967).Google Scholar