No CrossRef data available.
Article contents
PARABOLIC COMPACTIFICATION OF HOMOGENEOUS SPACES
Published online by Cambridge University Press: 30 October 2019
Abstract
In this article, we study compactifications of homogeneous spaces coming from equivariant, open embeddings into a generalized flag manifold 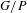 $G/P$. The key to this approach is that in each case
$G/P$. The key to this approach is that in each case 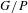 $G/P$ is the homogeneous model for a parabolic geometry; the theory of such geometries provides a large supply of geometric tools and invariant differential operators that can be used for this study. A classical theorem of Wolf shows that any involutive automorphism of a semisimple Lie group
$G/P$ is the homogeneous model for a parabolic geometry; the theory of such geometries provides a large supply of geometric tools and invariant differential operators that can be used for this study. A classical theorem of Wolf shows that any involutive automorphism of a semisimple Lie group 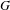 $G$ with fixed point group
$G$ with fixed point group 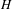 $H$ gives rise to a large family of such compactifications of homogeneous spaces of
$H$ gives rise to a large family of such compactifications of homogeneous spaces of 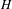 $H$. Most examples of (classical) Riemannian symmetric spaces as well as many non-symmetric examples arise in this way. A specific feature of the approach is that any compactification of that type comes with the notion of ‘curved analog’ to which the tools we develop also apply. The model example of this is a general Poincaré–Einstein manifold forming the curved analog of the conformal compactification of hyperbolic space. In the first part of the article, we derive general tools for the analysis of such compactifications. In the second part, we analyze two families of examples in detail, which in particular contain compactifications of the symmetric spaces
$H$. Most examples of (classical) Riemannian symmetric spaces as well as many non-symmetric examples arise in this way. A specific feature of the approach is that any compactification of that type comes with the notion of ‘curved analog’ to which the tools we develop also apply. The model example of this is a general Poincaré–Einstein manifold forming the curved analog of the conformal compactification of hyperbolic space. In the first part of the article, we derive general tools for the analysis of such compactifications. In the second part, we analyze two families of examples in detail, which in particular contain compactifications of the symmetric spaces 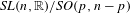 $\mathit{SL}(n,\mathbb{R})/\mathit{SO}(p,n-p)$ and
$\mathit{SL}(n,\mathbb{R})/\mathit{SO}(p,n-p)$ and 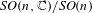 $\mathit{SO}(n,\mathbb{C})/\mathit{SO}(n)$. We describe the decomposition of the compactification into orbits, show how orbit closures can be described as the zero sets of smooth solutions to certain invariant differential operators and prove a local slice theorem around each orbit in these examples.
$\mathit{SO}(n,\mathbb{C})/\mathit{SO}(n)$. We describe the decomposition of the compactification into orbits, show how orbit closures can be described as the zero sets of smooth solutions to certain invariant differential operators and prove a local slice theorem around each orbit in these examples.
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 4 , July 2021 , pp. 1371 - 1408
- Copyright
- © The Author(s), 2019. Published by Cambridge University Press
Footnotes
A.Č. and A.R.G. gratefully acknowledge support from the Royal Society of New Zealand via Marsden grant 16-UOA-051; A.Č. gratefully acknowledges support by project P27072-N25 of the Austrian Science Fund (FWF). All authors acknowledge the hospitality of the University of Auckland and the University of Vienna. We thank the anonymous referee for very helpful comments.


