Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T15:57:28.942Z Has data issue: false hasContentIssue false
  • English
  • Français

POINCARÉ AND SOBOLEV INEQUALITIES FOR DIFFERENTIAL FORMS IN HEISENBERG GROUPS AND CONTACT MANIFOLDS

Part of: Miscellaneous topics - Partial differential equations Abstract harmonic analysis Symplectic geometry, contact geometry Linear function spaces and their duals Inequalities General theory of differentiable manifolds

Published online by Cambridge University Press:  29 June 2020

Annalisa Baldi Open the ORCID record for Annalisa Baldi [Opens in a new window] ,
Bruno Franchi Open the ORCID record for Bruno Franchi [Opens in a new window]  and
Pierre Pansu
Annalisa Baldi
Affiliation:
Università di Bologna, Dipartimento di Matematica, Piazza di Porta S. Donato 5, 40126Bologna, Italy (annalisa.baldi2@unibo.it; bruno.franchi@unibo.it)
Bruno Franchi
Affiliation:
Università di Bologna, Dipartimento di Matematica, Piazza di Porta S. Donato 5, 40126Bologna, Italy (annalisa.baldi2@unibo.it; bruno.franchi@unibo.it)
Pierre Pansu
Affiliation:
Université Paris-Saclay, CNRS, Laboratoire de mathématiques d’Orsay, 91405, Orsay, France (pierre.pansu@universite-paris-saclay.fr)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we prove contact Poincaré and Sobolev inequalities in Heisenberg groups 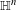$\mathbb{H}^{n}$, where the word ‘contact’ is meant to stress that de Rham’s exterior differential is replaced by the exterior differential of the so-called Rumin complex 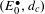$(E_{0}^{\bullet },d_{c})$, which recovers the scale invariance under the group dilations associated with the stratification of the Lie algebra of 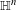$\mathbb{H}^{n}$. In addition, we construct smoothing operators for differential forms on sub-Riemannian contact manifolds with bounded geometry, which act trivially on cohomology. For instance, this allows us to replace a closed form, up to adding a controlled exact form, with a much more regular differential form.

Keywords

Heisenberg groupsdifferential formsSobolev–Poincaré inequalitiescontact manifoldshomotopy formula

MSC classification

Primary: 58A10: Differential forms 35R03: Partial differential equations on Heisenberg groups, Lie groups, Carnot groups, etc. 53D10: Contact manifolds, general
Secondary: 26D15: Inequalities for sums, series and integrals 43A80: Analysis on other specific Lie groups 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 3 , May 2022 , pp. 869 - 920
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Baldi, A., Barnabei, M. and Franchi, B., A recursive basis for primitive forms in symplectic spaces and applications to Heisenberg groups, Acta Math. Sin. (Engl. Ser.) 32(3) (2016), 265–285. MR 3456421.CrossRefGoogle Scholar
Baldi, A. and Franchi, B., Sharp a priori estimates for div-curl systems in Heisenberg groups, J. Funct. Anal. 265(10) (2013), 2388–2419. MR 3091819.CrossRefGoogle Scholar
Baldi, A., Franchi, B. and Pansu, P., Gagliardo-Nirenberg inequalities for differential forms in Heisenberg groups, Math. Ann. 365(3–4) (2016), 1633–1667. MR 3521101.Google Scholar
Baldi, A., Franchi, B. and Pansu, P., L 1 -Poincaré and Sobolev inequalities for differential forms in Euclidean spaces, Sci. China Math. 62(6) (2019), 1029–1040. MR 3951879.CrossRefGoogle Scholar
Baldi, A., Franchi, B. and Pansu, P., Duality and $L^{\infty }$ differential forms on Heisenberg groups, in preparation, 2020.Google Scholar
Baldi, A., Franchi, B. and Pansu, P., L 1 -Poincaré inequalities for differential forms on Euclidean spaces and Heisenberg groups, Adv. Math. 366 (2020), 107084. MR 4070308.CrossRefGoogle Scholar
Baldi, A., Franchi, B. and Pansu, P., Orlicz spaces and endpoint Sobolev–Poincaré inequalities for differential forms in Heisenberg groups, Matematiche (Catania) 75 (2020), 167–194.Google Scholar
Baldi, A., Franchi, B., Tchou, N. and Tesi, M. C., Compensated compactness for differential forms in Carnot groups and applications, Adv. Math. 223(5) (2010), 1555–1607.CrossRefGoogle Scholar
Baldi, A., Franchi, B. and Tesi, M. C., Compensated compactness in the contact complex of Heisenberg groups, Indiana Univ. Math. J. 57 (2008), 133–186.CrossRefGoogle Scholar
Baldi, A., Franchi, B. and Tesi, M. C., Hypoellipticity, fundamental solution and Liouville type theorem for matrix–valued differential operators in Carnot groups, J. Eur. Math. Soc. (JEMS) 11(4) (2009), 777–798.CrossRefGoogle Scholar
Baldi, A., Franchi, B. and Tripaldi, F., Gagliardo–Nirenberg inequalities for horizontal vector fields in the Engel group and in the seven-dimensional quaternionic Heisenberg group, in Geometric Methods in PDE’s, Springer INdAM Series, Volume 13, pp. 287–312 (Springer, Cham, 2015). MR 3617226.CrossRefGoogle Scholar
Balogh, Z. M., Fässler, K. and Peltonen, K., Uniformly quasiregular maps on the compactified Heisenberg group, J. Geom. Anal. 22(3) (2012), 633–665. MR 2927672.CrossRefGoogle Scholar
Bernig, A., Natural operations on differential forms on contact manifolds, Differential Geom. Appl. 50 (2017), 34–51. MR 3588639.CrossRefGoogle Scholar
Bonfiglioli, A., Lanconelli, E. and Uguzzoni, F., Stratified Lie groups and Potential Theory for Their Sub-Laplacians, Springer Monographs in Mathematics, (Springer, Berlin, 2007). MR 2363343.Google Scholar
Bourgain, J. and Brezis, Haïm, New estimates for elliptic equations and Hodge type systems, J. Eur. Math. Soc. (JEMS) 9(2) (2007), 277–315. MR 2293957 (2009h:35062).CrossRefGoogle Scholar
Bryant, R., Eastwood, M., Rod Gover, A. and Neusser, K., Some differential complexes within and beyond parabolic geometry, Preprint, 2011, arXiv:1112.2142.Google Scholar
Capogna, L., Danielli, D. and Garofalo, N., Subelliptic mollifiers and a basic pointwise estimate of Poincaré type, Math. Z. 226(1) (1997), 147–154. MR 1472145.CrossRefGoogle Scholar
Chanillo, S. and Van Schaftingen, J., Subelliptic Bourgain-Brezis estimates on groups, Math. Res. Lett. 16(3) (2009), 487–501. MR 2511628 (2010f:35042).CrossRefGoogle Scholar
Fässler, K., Lukyanenko, A. and Peltonen, K., Quasiregular mappings on sub-Riemannian manifolds, J. Geom. Anal. 26(3) (2016), 1754–1794. MR 3511457.CrossRefGoogle Scholar
Folland, G. B., Subelliptic estimates and function spaces on nilpotent Lie groups, Ark. Mat. 13(2) (1975), 161–207. MR 0494315 (58 #13215).CrossRefGoogle Scholar
Folland, G. B. and Stein, E. M., Hardy Spaces on Homogeneous Groups, Mathematical Notes, Volume 28, (Princeton University Press, Princeton, NJ, 1982). MR 657581 (84h:43027).Google Scholar
Franchi, B., Gutiérrez, C. E. and Wheeden, R. L., Weighted Sobolev–Poincaré inequalities for Grushin type operators, Comm. Partial Differential Equations 19(3–4) (1994), 523–604. MR 1265808.CrossRefGoogle Scholar
Franchi, B., Lu, G. and Wheeden, R. L., Representation formulas and weighted Poincaré inequalities for Hörmander vector fields, Ann. Inst. Fourier (Grenoble) 45(2) (1995), 577–604. MR 1343563 (96i:46037).CrossRefGoogle Scholar
Franchi, B., Lu, G. and Wheeden, R. L., A relationship between Poincaré-type inequalities and representation formulas in spaces of homogeneous type, Int. Math. Res. Not. IMRN (1) (1996), 1–14. MR 1383947 (97k:26012).CrossRefGoogle Scholar
Franchi, B., Serapioni, R. and Cassano, F. S., Meyers–Serrin type theorems and relaxation of variational integrals depending on vector fields, Houston J. Math. 22(4) (1996), 859–890. MR 1437714.Google Scholar
Franchi, B. and Serapioni, R. P., Intrinsic Lipschitz graphs within Carnot groups, J. Geom. Anal. 26(3) (2016), 1946–1994. MR 3511465.CrossRefGoogle Scholar
Franchi, B., Serapioni, R. and Cassano, F. S., Regular submanifolds, graphs and area formula in Heisenberg groups, Adv. Math. 211(1) (2007), 152–203. MR 2313532 (2008h:49030).CrossRefGoogle Scholar
Gallot, S., Hulin, D. and Lafontaine, J., Riemannian Geometry, third edition, Universitext, (Springer, Berlin, 2004). MR 2088027.CrossRefGoogle Scholar
Gol’dshtein, V. M., Kuz’minov, V. I. and Shvedov, I. A., L p-cohomology of warped cylinders, Sibirsk. Mat. Zh. 31(6) (1990), 55–63. MR 1097955.Google Scholar
Gromov, M., Carnot–Carathéodory spaces seen from within, in Sub-Riemannian Geometry, Progress in Mathematics, Volume 144, pp. 79–323 (Birkhäuser, Basel, 1996). MR 1421823 (2000f:53034).CrossRefGoogle Scholar
Heinonen, J. and Holopainen, I., Quasiregular maps on Carnot groups, J. Geom. Anal. 7(1) (1997), 109–148. MR 1630785.CrossRefGoogle Scholar
Helffer, B. and Nourrigat, J., Hypoellipticité maximale pour des opérateurs polynômes de champs de vecteurs, Progress in Mathematics, Volume 58, (Birkhäuser Boston Inc., Boston, MA, 1985). MR 897103 (88i:35029).Google Scholar
Iwaniec, T. and Lutoborski, A., Integral estimates for null Lagrangians, Arch. Ration. Mech. Anal. 125(1) (1993), 25–79. MR 1241286 (95c:58054).CrossRefGoogle Scholar
Jerison, D., The Poincaré inequality for vector fields satisfying Hörmander’s condition, Duke Math. J. 53(2) (1986), 503–523. MR 850547 (87i:35027).CrossRefGoogle Scholar
Kim, Y., Quasiconformal conjugacy classes of parabolic isometries of complex hyperbolic space, Pacific J. Math. 270(1) (2014), 129–149. MR 3245851.CrossRefGoogle Scholar
Lanzani, L. and Stein, E. M., A note on div curl inequalities, Math. Res. Lett. 12(1) (2005), 57–61. MR 2122730 (2005m:58001).CrossRefGoogle Scholar
Lukyanenko, A., Geometric mapping theory of the Heisenberg group, sub-Riemannian manifolds, and hyperbolic spaces, ProQuest LLC, Ann Arbor, MI, 2014, Ph.D. Thesis, University of Illinois at Urbana-Champaign. MR 3322035.Google Scholar
Maheux, P. and Saloff-Coste, L., Analyse sur les boules d’un opérateur sous-elliptique, Math. Ann. 303(4) (1995), 713–740. MR 1359957 (96m:35049).Google Scholar
Martinet, J., Formes de contact sur les variétés de dimension 3, Lecture Notes in Mathematics, Volume 209, pp. 142–163 (Springer, Berlin, 1971). MR 0350771.Google Scholar
Mattila, P., Geometry of Sets and Measures in Euclidean Spaces: Fractals and Rectifiability, Cambridge Studies in Advanced Mathematics, Volume 44, (Cambridge University Press, Cambridge, 1995). MR 1333890.CrossRefGoogle Scholar
McDuff, D. and Salamon, D., Introduction to Symplectic Topology, second edition, Oxford Mathematical Monographs, (The Clarendon Press, Oxford University Press, New York, 1998). MR 1698616.Google Scholar
Mitrea, D., Mitrea, M. and Monniaux, S., The Poisson problem for the exterior derivative operator with Dirichlet boundary condition in nonsmooth domains, Commun. Pure Appl. Anal. 7(6) (2008), 1295–1333. MR 2425010.CrossRefGoogle Scholar
Montgomery, R., A tour of Subriemannian Geometries, their Geodesics and Applications, Mathematical Surveys and Monographs, Volume 91, (American Mathematical Society, Providence, RI, 2002). MR 1867362 (2002m:53045).Google Scholar
Müller, D., Peloso, M. M. and Ricci, F., Analysis of the Hodge Laplacian on the Heisenberg group, Mem. Amer. Math. Soc. 233(1095) (2015), vi+91.MR 3289035.Google Scholar
Pansu, P., Métriques de Carnot–Carathéodory et quasiisométries des espaces symétriques de rang un, Ann. of Math. (2) 129(1) (1989), 1–60. MR 979599 (90e:53058).CrossRefGoogle Scholar
Pansu, P., Cohomologie L p en degré 1 des espaces homogènes, Potential Anal. 27(2) (2007), 151–165. MR 2322503.CrossRefGoogle Scholar
Pansu, P., Cup-products in $l^{q,p}$ -cohomology: discretization and quasi-isometry invariance, Preprint, 2017, arXiv:1702.04984.Google Scholar
Pansu, P. and Rumin, M., On the ℓ q, p cohomology of Carnot groups, Ann. H. Lebesgue 1 (2018), 267–295. MR 3963292.CrossRefGoogle Scholar
Pansu, P. and Tripaldi, F., Averages and the ℓ q, 1 cohomology of Heisenberg groups, Ann. Math. Blaise Pascal 26(1) (2019), 81–100. (en).CrossRefGoogle Scholar
Rumin, M., Formes différentielles sur les variétés de contact, J. Differential Geom. 39(2) (1994), 281–330. MR 1267892 (95g:58221).Google Scholar
Rumin, M., Differential geometry on C-C spaces and application to the Novikov-Shubin numbers of nilpotent Lie groups, C. R. Acad. Sci. Paris Sér. I Math. 329(11) (1999), 985–990. MR 1733906 (2001g:53063).CrossRefGoogle Scholar
Rumin, M., Sub-Riemannian limit of the differential form spectrum of contact manifolds, Geom. Funct. Anal. 10(2) (2000), 407–452. MR 1771424 (2002f:53044).CrossRefGoogle Scholar
Rumin, M., Around heat decay on forms and relations of nilpotent Lie groups, Séminaire de Théorie Spectrale et Géométrie, Volume 19, pp. 123–164. MR 1909080 (2003f:58062).Google Scholar
Rumin, M., An introduction to spectral and differential geometry in Carnot–Carathéodory spaces, Rend. Circ. Mat. Palermo (2) Suppl. 75 (2005), 139–196. MR 2152359 (2006g:58053).Google Scholar
Schwarz, G., Hodge Decomposition—A Method for Solving Boundary Value Problems, Lecture Notes in Mathematics, Volume 1607, (Springer, Berlin, 1995). MR 1367287 (96k:58222).CrossRefGoogle Scholar
Stein, E. M., Harmonic Analysis: Real-variable Methods, Orthogonality, and Oscillatory Integrals, Princeton Mathematical Series, Volume 43, (Princeton University Press, Princeton, NJ, 1993). With the assistance of Timothy S. Murphy, Monographs in Harmonic Analysis, III.MR 1232192 (95c:42002).Google Scholar
Varopoulos, N. Th., Saloff-Coste, L. and Coulhon, T., Analysis and Geometry on Groups, Cambridge Tracts in Mathematics, Volume 100, (Cambridge University Press, Cambridge, 1992). MR 1218884 (95f:43008).Google Scholar
Warner, F. W., Foundations of Differentiable Manifolds and Lie Groups, Graduate Texts in Mathematics, Volume 94, (Springer, New York, 1983). Corrected reprint of the 1971 edition.MR 722297.CrossRefGoogle Scholar