PROJECTIVE LOOPS GENERATE RATIONAL LOOP GROUPS

Abstract

We generalize Uhlenbeck’s generator theorem of 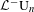${\mathcal{L}}^{-}\operatorname{U}_{n}$ to the full rational loop group 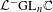${\mathcal{L}}^{-}\operatorname{GL}_{n}\mathbb{C}$ and its subgroups 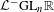${\mathcal{L}}^{-}\operatorname{GL}_{n}\mathbb{R}$, 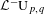${\mathcal{L}}^{-}\operatorname{U}_{p,q}$: they are all generated by just simple projective loops. Recall that Terng–Uhlenbeck studied the dressing actions of such projective loops as generalized Bäcklund transformations for integrable systems. Our result makes a nice supplement: any rational dressing is the composition of these Bäcklund transformations. This conclusion is surprising in the sense that Lie theory suggests the indispensable role of nilpotent loops in the case of noncompact reality conditions, and nilpotent dressings appear quite complicated and mysterious. The sacrifice is to introduce some extra fake singularities. So we also propose a set of generators if fake singularities are forbidden. A very geometric and physical construction of 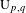$\operatorname{U}_{p,q}$ is obtained as a by-product, generalizing the classical construction of unitary groups.