Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T03:23:25.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Pseudospectra of semiclassical boundary value problems

Published online by Cambridge University Press:  14 March 2014

Jeffrey Galkowski
Jeffrey Galkowski*
Affiliation:
Mathematics Department, University of California, Berkeley, CA 94720, USA(jeffrey.galkowski@math.berkeley.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider operators 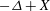$ - \Delta + X $, where 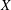$ X $ is a constant vector field, in a bounded domain, and show spectral instability when the domain is expanded by scaling. More generally, we consider semiclassical elliptic boundary value problems which exhibit spectral instability for small values of the semiclassical parameter 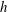$h$, which should be thought of as the reciprocal of the Péclet constant. This instability is due to the presence of the boundary: just as in the case of 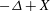$ - \Delta + X $, some of our operators are normal when considered on 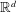$\mathbb{R}^d$. We characterize the semiclassical pseudospectrum of such problems as well as the areas of concentration of quasimodes. As an application, we prove a result about exit times for diffusion processes in bounded domains. We also demonstrate instability for a class of spectrally stable nonlinear evolution problems that are associated with these elliptic operators.

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 14 , Issue 2 , April 2015 , pp. 405 - 449
Copyright
© Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Crandall, M., Ishii, G. and Lions, P.-L., User’s guide to viscosity solutions of second order partial differential equations, Bull. Amer. Math. Soc. (N.S.) 27(1), (1992), 1–67.Google Scholar
Davies, E. B., Semi-classical states for non-self-adjoint Schrödinger operators, Commun. Math. Phys. 200(1), (1999), 35–41.Google Scholar
Dencker, N., The pseudospectrum of systems of semiclassical operators, Anal. PDE 1(3), (2008), 323–373.CrossRefGoogle Scholar
Dencker, N., Sjöstrand, J. and Zworski, M., Pseudospectra of semiclassical (pseudo-) differential operators, Commun. Pure Appl. Maths 57(3), (2004), 384–415.Google Scholar
Duistermaat, J. J. and Hörmander, L., Fourier integral operators. II, Acta Mathematica 128(3–4), (1972), 183–269.Google Scholar
Evans, L. C., Partial Differential Equations 2nd edn Graduate Studies in Mathematics, vol. 19 (American Mathematical Society, Providence, RI, 2010).Google Scholar
Freidlin, M. I. and Wentzell, A. D., Random Perturbations of Dynamical Systems 2nd edn Brundlehren der Mathematischen Wissenschaften, vol. 260 (Springer-Verlag, New York, 1998).CrossRefGoogle Scholar
Galkowski, J., Nonlinear instability in a semiclassical problem, Commun. Math. Phys. 316(3), (2012), 705–722.CrossRefGoogle Scholar
Gallagher, I., Gallay, T. and Nier, F., Spectral asymptotics for large skew-symmetric perturbations of the harmonic oscillator, Int. Math. Res. Not. IMRN(12), (2009), 2147–2199.Google Scholar
Hansen, A., On the solvability complexity index, the n-pseudospectrum and approximations of spectra of operators, J. Am. Math. Soc. 24(1), (2011), 81–124.CrossRefGoogle Scholar
Hitrik, M. and Pravda-Starov, K., Semiclassical hypoelliptic estimates for non-selfadjoint operators with double characteristics, Commun. Part. Diff. Equ. 35(6), (2010), 988–1028.Google Scholar
Hitrik, M. and Pravda-Starov, K., Spectra and semigroup smoothing for non-elliptic quadratic operators, Math. Ann. 344(4), (2009), 801–846.CrossRefGoogle Scholar
Hörmander, L., The Analysis of Linear Partial Differential Operators. I. Distribution Theory and Fourier Analysis Classics in Mathematics, (Springer-Verlag, Berlin, 2003).Google Scholar
Hörmander, L., The Analysis of Linear Partial Differential Operators. III. Pseudo-Differential Operators Classics in Mathematics, (Springer-Verlag, Berlin, 2007).Google Scholar
Kenig, C. E., Sjöstrand, J. and Uhlmann, G., The Calderón problem with partial data, Ann. of Math. (2) 165(2), (2007), 567–591.Google Scholar
Magazanik, E. and Perles, M. A., Relatively convex subsets of simply connected planar sets, Israel J. Math. 160, (2007), 143–155.Google Scholar
Roberts, W. A. and Varberg, D. E., Convex Functions Pure and Applied Mathematics, vol. 57 (Academic Press [A subsidiary of Harcourt Brace Jovanovich, Publishers], New York, London, 1973).Google Scholar
Pravda-Starov, K., Pseudo-spectrum for a class of semi-classical operators, Bull. Soc. Maths France 136(3), (2008), 329–372.Google Scholar
Reichel, L. and Trefethen, L. N., Eigenvalues and pseudo-eigenvalues of Toeplitz matrices. Directions in matrix theory (Auburn, AL, 1990), Linear Algebr. Applics. 162–164, (1992), 153–185.Google Scholar
Sandstede, B. and Scheel, A., Basin boundaries and bifurcations near convective instabilities: a case study, J. Differ. Equ. 208(1), (2005), 176–193.Google Scholar
Sjöstrand, J., Singularités Analytiques Microlocales Astérisque, vol. 95 (Soc. Math. France, Paris, 1982).Google Scholar
Trefethen, L. N. and Embree, M., Spectra and Pseudospectra. The Behaviour of Nonnormal Matrices and Operators. (Princeton University Press, Princeton, NJ, 2005).CrossRefGoogle Scholar
Zworski, M., A remark on a paper of E.B. Davies, Proc. Am. Math. Soc. 129(10), (2001), 2955–2957.CrossRefGoogle Scholar
Zworski, M., Semiclassical Analysis Graduate Studies in Mathematics, vol. 138 (American Mathematical Society, Providence, RI, 2012).Google Scholar