Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T04:21:12.216Z Has data issue: false hasContentIssue false
  • English
  • Français

RAMSEY GROWTH IN SOME NIP STRUCTURES

Part of: Graph theory Extremal combinatorics Model theory

Published online by Cambridge University Press:  19 February 2019

Artem Chernikov ,
Sergei Starchenko  and
Margaret E. M. Thomas
Artem Chernikov
Affiliation:
Department of Mathematics, University of California Los Angeles, Los Angeles, CA90095-1555, USA (chernikov@math.ucla.edu)
Sergei Starchenko
Affiliation:
Department of Mathematics, University of Notre Dame, Notre Dame, IN46556, USA (Starchenko.1@nd.edu)
Margaret E. M. Thomas
Affiliation:
Zukunftskolleg, Department of Mathematics and Statistics, University of Konstanz, Box 216, 78457Konstanz, Germany (margaret.thomas@uni-konstanz.de)
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate bounds in Ramsey’s theorem for relations definable in NIP structures. Applying model-theoretic methods to finitary combinatorics, we generalize a theorem of Bukh and Matousek (Duke Mathematical Journal163(12) (2014), 2243–2270) from the semialgebraic case to arbitrary polynomially bounded $o$-minimal expansions of 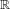$\mathbb{R}$, and show that it does not hold in 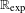$\mathbb{R}_{\exp }$. This provides a new combinatorial characterization of polynomial boundedness for $o$-minimal structures. We also prove an analog for relations definable in $P$-minimal structures, in particular for the field of the 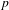$p$-adics. Generalizing Conlon et al. (Transactions of the American Mathematical Society366(9) (2014), 5043–5065), we show that in distal structures the upper bound for 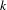$k$-ary definable relations is given by the exponential tower of height $k-1$.

Keywords

o-minimalityNIPRamsey’s theoremp-minimalitypolynomially bounded

MSC classification

Primary: 03C45: Classification theory, stability and related concepts 05C35: Extremal problems 05D10: Ramsey theory 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 1 , January 2021 , pp. 1 - 29
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, H., An introduction to theories without the independence property, Arch. Math. Logic 5 (2008), http://www.logic.univie.ac.at/~adler/docs/nip.pdf.Google Scholar
Alon, N., Pach, J., Pinchasi, R., Radoicić, R. and Sharir, M., Crossing patterns of semi-algebraic sets, J. Combin. Theory Ser. A 111(2) (2005), 310–326.CrossRefGoogle Scholar
Aschenbrenner, M., Dolich, A., Haskell, D., Macpherson, D. and Starchenko, S., Vapnik–Chervonenkis density in some theories without the independence property, I, Trans. Amer. Math. Soc. 368(8) (2016), 5889–5949.10.1090/tran/6659CrossRefGoogle Scholar
Basu, S., Combinatorial complexity in o-minimal geometry, Proc. Lond. Math. Soc. 100(2) (2010), 405–428.CrossRefGoogle Scholar
Behrend, F. A., On sets of integers which contain no three terms in arithmetical progression, Proc. Natl. Acad. Sci. USA 32 (1946), 331–332.CrossRefGoogle ScholarPubMed
Bukh, B. and Matousek, J., Erdős–Szekeres-type statements: Ramsey function and decidability in dimension 1, Duke Math. J. 163(12) (2014), 2243–2270.CrossRefGoogle Scholar
Chernikov, A., Galvin, D. and Starchenko, S., Cutting lemma and Zarankiewicz’s problem in distal structures, Preprint, 2016, arXiv:1612.00908.Google Scholar
Chernikov, A. and Simon, P., Externally definable sets and dependent pairs II, Trans. Amer. Math. Soc. 367(7) (2015), 5217–5235.10.1090/S0002-9947-2015-06210-2CrossRefGoogle Scholar
Chernikov, A. and Starchenko, S., Definable regularity lemmas for NIP hypergraphs, Preprint, 2016, arXiv:1607.07701.Google Scholar
Chernikov, A. and Starchenko, S., A note on the Erdős-Hajnal property for stable graphs, Proc. Amer. Math. Soc. 146(2) (2018), 785–790.CrossRefGoogle Scholar
Chernikov, A. and Starchenko, S., Regularity lemma for distal structures, J. Eur. Math. Soc. (JEMS) 20(10) (2018), 2437–2466.CrossRefGoogle Scholar
Chudnovsky, M., The Erdös–Hajnal Conjecture: A survey, J. Graph Theory 75(2) (2014), 178–190.CrossRefGoogle Scholar
Conlon, D., Fox, J., Pach, J., Sudakov, B. and Suk, A., Ramsey-type results for semi-algebraic relations, Trans. Amer. Math. Soc. 366(9) (2014), 5043–5065.CrossRefGoogle Scholar
Conlon, D., Fox, J. and Sudakov, B., Hypergraph Ramsey numbers, J. Amer. Math. Soc. 23(1) (2010), 247–266.CrossRefGoogle Scholar
Darniere, L. and Halupczok, I., Cell decomposition and classification of definable sets in p-optimal fields, J. Symbolic Logic 82(1) (2017), 120–136.10.1017/jsl.2015.79CrossRefGoogle Scholar
van den Dries, L., Tame Topology and o-minimal Structures vol. 248, London Mathematical Society Lecture Note Series, Volume 248 (Cambridge University Press, Cambridge, 1998). x+180 pp.CrossRefGoogle Scholar
van den Dries, L., Haskell, D. and Macpherson, D., One-dimensional p-adic subanalytic sets, J. Lond. Math. Soc. 59(1) (1999), 1–20.CrossRefGoogle Scholar
Elias, M., Matousek, J., Roldán-Pensado, E. and Safernová, Z., Lower bounds on geometric Ramsey functions, SIAM J. Discrete Math. 28(4) (2014), 1960–1970.CrossRefGoogle Scholar
Ensley, D. and Grossberg, R., Ramsey’s theorem in stable structures, manuscript (1997). URL: http://www.math.cmu.edu/~rami/finite.pdf.Google Scholar
Erdős, P. and Szekeres, G., A combinatorial problem in geometry, Compos. Math. 2 (1935), 463–470.Google Scholar
Erdős, P., Some remarks on the theory of graphs, Bull. Amer. Math. Soc. 53(4) (1947), 292–294.CrossRefGoogle Scholar
Erdős, P., Hajnal, A. and Rado, R., Partition relations for cardinal numbers, Acta Math. Hungar. 16(1–2) (1965), 93–196.CrossRefGoogle Scholar
Erdős, P. and Rado, R., Combinatorial theorems on classifications of subsets of a given set, Proc. Lond. Math. Soc. 3(1) (1952), 417–439.CrossRefGoogle Scholar
Erdős, P. and Szekeres, G., A combinatorial problem in geometry, Compos. Math. 2 (1935), 463–470.Google Scholar
Fox, J. and Pach, J., Erdős-Hajnal-type results on intersection patterns of geometric objects, in Horizons of Combinatorics, Bolyai Soc. Math. Stud., Volume 17, pp. 79–103 (Springer, Berlin, 2008).10.1007/978-3-540-77200-2_4CrossRefGoogle Scholar
Graham, R. L., Rothschild, B. L. and Spencer, J. H., Ramsey Theory, Wiley-Interscience Series in Discrete Mathematics. A Wiley-Interscience Publication (John Wiley & Sons, Inc., New York, 1980). ix+174 pp.Google Scholar
Guingona, V., On uniform definability of types over finite sets, J. Symbolic Logic 77(02) (2012), 499–514.CrossRefGoogle Scholar
Haskell, D. and Macpherson, D., A version of o-minimality for the p-adics, J. Symbolic Logic 62(04) (1997), 1075–1092.CrossRefGoogle Scholar
Hrushovski, E. and Pillay, A., On NIP and invariant measures, J. Eur. Math. Soc. (JEMS) 13(4) (2011), 1005–1061.10.4171/JEMS/274CrossRefGoogle Scholar
Johnson, H. and Laskowski, M., Compression schemes, stable definable families, and o-minimal structures, Discrete Comput. Geom. 43(4) (2010), 914–926.CrossRefGoogle Scholar
Kaplan, I. and Shelah, S., A dependent theory with few indiscernibles, Israel J. Math. 202(1) (2014), 59–103.CrossRefGoogle Scholar
Kovacsics, P. C. and Delon, F., Definable functions in tame expansions of algebraically closed valued fields, Preprint, 2018, arXiv:1802.03323.Google Scholar
Laskowski, M., Vapnik-Chervonenkis classes of definable sets, J. Lond. Math. Soc. 2(2) (1992), 377–384.CrossRefGoogle Scholar
Macintyre, A., On definable subsets of p-adic fields, J. Symbolic Logic 41(3) (1976), 605–610.CrossRefGoogle Scholar
Malliaris, M. and Shelah, S., Regularity lemmas for stable graphs, Trans. Amer. Math. Soc. 366(3) (2014), 1551–1585.10.1090/S0002-9947-2013-05820-5CrossRefGoogle Scholar
Matousek, J., Lectures on Discrete Geometry, Graduate Texts in Mathematics, Volume 212 (Springer, New York, 2002).CrossRefGoogle Scholar
Miller, C., Exponentiation is hard to avoid, Proc. Amer. Math. Soc. 122(1) (1994), 257–259.CrossRefGoogle Scholar
Miller, C. and Starchenko, S., A growth dichotomy for o-minimal expansions of ordered groups, Trans. Amer. Math. Soc. 350(9) (1998), 3505–3521.CrossRefGoogle Scholar
Moran, S. and Yehudayoff, A., Sample compression schemes for VC classes, J. ACM (JACM) 63(3) (2016), 21.CrossRefGoogle Scholar
Prestel, A. and Roquette, P., Peter Formally p-Adic Fields, Lecture Notes in Mathematics, Volume 1050, (Springer, Berlin, 1984). v+167 pp.CrossRefGoogle Scholar
Ramsey, F. P., On a problem of formal logic, Proc. Lond. Math. Soc. 2(1) (1930), 264–286.10.1112/plms/s2-30.1.264CrossRefGoogle Scholar
Sauer, N., On the density of families of sets, J. Combin. Theory Ser. A 13(1) (1972), 145–147.CrossRefGoogle Scholar
Scanlon, T., O-minimality as an approach to the André–Oort conjecture, in Around the Zilber–Pink conjecture/Autour de la conjecture de Zilber–Pink, Panor. Synthèses, Volume 52, pp. 111–165 (Soc. Math. France, Paris, 2017).Google Scholar
Shelah, S., Classification theory and the number of nonisomorphic models, in Studies in Logic and the Foundations of Mathematics vol. 92, 2nd edn (North-Holland Publishing Co., Amsterdam, 1990).Google Scholar
Shelah, S., A combinatorial problem; stability and order for models and theories in infinitary languages, Pacific J. Math. 41(1) (1972), 247–261.CrossRefGoogle Scholar
Shelah, S., Around Classification Theory of Models, Lecture Notes in Mathematics, Volume 1182 (Springer, Berlin, 1986). viii+279 pp.CrossRefGoogle Scholar
Shelah, S., Classification theory for elementary classes with the dependence property—a modest beginning, Sci. Math. Jpn. 59(2) (2004), 265–316. Special issue on set theory and algebraic model theory.Google Scholar
Shelah, S., Strongly dependent theories, Israel J. Math. 204(1) (2014), 1–83.CrossRefGoogle Scholar
Simon, P., Distal and non-distal NIP theories, Ann. Pure Appl. Logic 164(3) (2013), 294–318.10.1016/j.apal.2012.10.015CrossRefGoogle Scholar
Simon, P., A Guide to NIP Theories, Lecture Notes in Logic, Volume 44 (Association for Symbolic Logic, Chicago, IL; Cambridge Scientific Publishers, Cambridge, 2015). vii+156 pp.CrossRefGoogle Scholar
Wilkie, A. J., Model completeness results for expansions of the ordered field of real numbers by restricted Pfaffian functions and the exponential function, J. Amer. Math. Soc. 9(4) (1996), 1051–1094.CrossRefGoogle Scholar