Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-06T14:40:00.790Z Has data issue: false hasContentIssue false
  • English
  • Français

Random Dieudonné modules, random 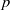$p$-divisible groups, and random curves over finite fields

Part of: Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry Algebraic groups

Published online by Cambridge University Press:  13 February 2013

Bryden Cais ,
Jordan S. Ellenberg  and
David Zureick-Brown
Bryden Cais
Affiliation:
Department of Mathematics, The University of Arizona, 617 N. Santa Rita Ave., P.O. Box 210089, Tucson, AZ 85721-0089, USA (cais@math.arizona.edu)
Jordan S. Ellenberg
Affiliation:
Department of Mathematics, University of Wisconsin-Madison, 480 Lincoln Drive, Madison, WI 53706, USA (ellenber@math.wisc.edu)
David Zureick-Brown
Affiliation:
Dept. of Math and Computer Science, Emory University, 400 Dowman Dr., W401, Atlanta, GA 30322, USA (dzb@mathcs.emory.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

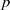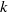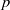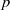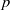We describe a probability distribution on isomorphism classes of principally quasi-polarized $p$-divisible groups over a finite field $k$ of characteristic $p$ which can reasonably be thought of as a ‘uniform distribution’, and we compute the distribution of various statistics ($p$-corank, $a$-number, etc.) of $p$-divisible groups drawn from this distribution. It is then natural to ask to what extent the 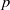$p$-divisible groups attached to a randomly chosen hyperelliptic curve (respectively, curve; respectively, abelian variety) over 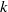$k$ are uniformly distributed in this sense. This heuristic is analogous to conjectures of Cohen–Lenstra type for 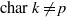$\text{char~} k\not = p$, in which case the random 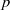$p$-divisible group is defined by a random matrix recording the action of Frobenius. Extensive numerical investigation reveals some cases of agreement with the heuristic and some interesting discrepancies. For example, plane curves over 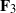${\mathbf{F} }_{3} $ appear substantially less likely to be ordinary than hyperelliptic curves over 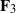${\mathbf{F} }_{3} $.

Keywords

algebraic curvearithmetic statisticsp-divisible groupDieduonne modulerandom matrices

MSC classification

Secondary: 14L05: Formal groups, $p$-divisible groups 11G20: Curves over finite and local fields 14G17: Positive characteristic ground fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 3 , July 2013 , pp. 651 - 676
Copyright
©Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achter, Jeffrey D., The distribution of class groups of function fields, J. Pure Appl. Algebra 204 (2) (2006), 316–333, MR 2184814 (2006h:11132).Google Scholar
Achter, Jeffrey D. and Pries, Rachel, Monodromy of the $p$-rank strata of the moduli space of curves, Int. Math. Res. Not. IMRN 15 (2008), Art. ID rnn053, 25; MR 2438069 (2009i:14030).Google Scholar
Achter, J. D. and Pries, R., The $p$-rank strata of the moduli space of hyperelliptic curves, Adv. Math. (2011).Google Scholar
Artin, E., Geometric algebra (Interscience Publishers, Inc., New York-London, 1957), MR 0082463 (18,553e).Google Scholar
Cais, Bryden, Ellenberg, Jordan and Zureick-Brown, David, Electronic transcript of computations for the paper ‘Random Dieudonné modules, random $p$-divisible groups, and random curves over finite fields’, Available at http://www.mathcs.emory.edu/~dzb/. (Also attached at the end of the tex file).Google Scholar
Cohen, H. and Lenstra, H., Heuristics on class groups of number fields, Number Theory Noordwijkerhout 1983 (1984), 33–62.CrossRefGoogle Scholar
Demazure, Michel, Lectures on $p$-divisible groups, Lecture Notes in Mathematics, Volume 302 (Springer, Berlin, 1972), MR 0344261 (49 #9000).Google Scholar
Johan de Jong, A. and Katz, Nicholas M., Counting the number of curves over a finite field, 2000, preprint.Google Scholar
Ellenberg, Jordan S., Venkatesh, Akshay and Westerland, Craig, Homological stability for Hurwitz spaces and the Cohen–Lenstra conjecture over function fields 2, 2012, preprint.Google Scholar
Fontaine, Jean-Marc, Groupes p-divisibles sur les corps locaux. (Société Mathématique de France, Paris, 1977), Astérisque, No. 47-48, MR 0498610 (58 #16699).Google Scholar
Fulman, Jason, A probabilistic approach to conjugacy classes in the finite symplectic and orthogonal groups, J. Algebra 234 (1) (2000), 207–224, MR 1799484 (2002j:20094).Google Scholar
Friedman, E. and Washington, L. C., On the distribution of divisor class groups of curves over a finite field, in Théorie des nombres (Quebec, PQ, 1987), pp. 227–239 (de Gruyter, Berlin, 1989).Google Scholar
Garton, Derek, Random matrices and the Cohen–Lenstra statistics for global fields with roots of unity, 2012, UW-Madison thesis, in preparation.Google Scholar
Grothendieck, Alexandre, Groupes de Barsotti–Tate et cristaux de Dieudonné. 1974) (Les Presses de l’Université de Montréal, Montreal, Que., Séminaire de Mathématiques Supérieures, No. 45 (Été, 1970), MR 0417192 (54 #5250).Google Scholar
Holland, Timothy, Counting semilinear endomorphisms over finite fields, 2011.Google Scholar
Malle, Gunter, On the distribution of class groups of number fields, Experiment. Math. 19 (4) (2010), 465–474, MR 2778658 (2011m:11224).Google Scholar
Manin, Ju. I., Theory of commutative formal groups over fields of finite characteristic, Uspehi Mat. Nauk 18 (6 (114)) (1963), 3–90, MR 0157972 (28 #1200).Google Scholar
Moonen, Ben, Group schemes with additional structures and Weyl group cosets, in Moduli of abelian varieties (Texel Island, 1999), Progr. Math., Volume 195, pp. 255–298 (Birkhäuser, Basel, 2001), MR 1827024 (2002c:14074).Google Scholar
Oda, Tadao, The first de Rham cohomology group and Dieudonné modules, Ann. Sci. École Norm. Sup. (4) 2 (1969), 63–135, MR 0241435 (39 #2775).Google Scholar
Oort, Frans, A stratification of a moduli space of abelian varieties, in Moduli of abelian varieties (Texel Island, 1999), Progr. Math., Volume 195, pp. 345–416 (Birkhäuser, Basel, 2001), MR 1827027 (2002b:14055).Google Scholar
Oort, Frans, Foliations in moduli spaces of abelian varieties, J. Amer. Math. Soc. 17 (2) (2004), 267–296 (electronic), MR 2051612 (2005c:14051).Google Scholar
Poonen, Bjorn and Rains, Eric, Random maximal isotropic subspaces and Selmer groups, J. Amer. Math. Soc. 25 (1) (2012), 245–269, MR 2833483.Google Scholar
Pries, Rachel, A short guide to $p$-torsion of abelian varieties in characteristic $p$, in Computational arithmetic geometry, Contemp. Math., Volume 463, pp. 121–129 (Amer. Math. Soc., Providence, RI, 2008), MR 2459994 (2009m:11085).Google Scholar
Rudvalis, A. and Shinoda, K., An enumeration in finite classical groups, 1988, preprint.Google Scholar
Stöhr, Karl-Otto and Voloch, José Felipe, A formula for the Cartier operator on plane algebraic curves, J. Reine Angew. Math. 377 (1987), 49–64, MR 887399 (88g:14026).Google Scholar
Tate, J. T., p-divisible groups, in Proc. Conf. Local Fields (Driebergen, 1966), pp. 158–183 (Springer, Berlin, 1967), MR 0231827 (38 #155).Google Scholar
Yui, Noriko, On the Jacobian varieties of hyperelliptic curves over fields of characteristic $p\gt 2$, J. Algebra 52 (2) (1978), 378–410, MR 0491717 (58 #10920).Google Scholar