Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T22:00:46.608Z Has data issue: false hasContentIssue false
  • English
  • Français

RC-POSITIVITY, VANISHING THEOREMS AND RIGIDITY OF HOLOMORPHIC MAPS

Part of: Global differential geometry (Co)homology theory Holomorphic fiber spaces

Published online by Cambridge University Press:  11 October 2019

Xiaokui Yang Open the ORCID record for Xiaokui Yang [Opens in a new window]
Xiaokui Yang*
Affiliation:
Department of Mathematics and Yau Mathematical Sciences Center, Tsinghua University, Beijing100084, China (xkyang@mail.tsinghua.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 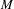$M$ and 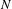$N$ be two compact complex manifolds. We show that if the tautological line bundle 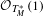${\mathcal{O}}_{T_{M}^{\ast }}(1)$ is not pseudo-effective and 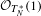${\mathcal{O}}_{T_{N}^{\ast }}(1)$ is nef, then there is no non-constant holomorphic map from 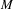$M$ to 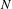$N$. In particular, we prove that any holomorphic map from a compact complex manifold 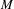$M$ with RC-positive tangent bundle to a compact complex manifold 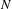$N$ with nef cotangent bundle must be a constant map. As an application, we obtain that there is no non-constant holomorphic map from a compact Hermitian manifold with positive holomorphic sectional curvature to a Hermitian manifold with non-positive holomorphic bisectional curvature.

Keywords

RC-positivityvanishing theoremsrigidity

MSC classification

Primary: 53C55: Hermitian and Kählerian manifolds 32L20: Vanishing theorems
Secondary: 14F17: Vanishing theorems
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 3 , May 2021 , pp. 1023 - 1038
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was partially supported by China’s Recruitment Program of Global Experts and NSFC 11688101.

References

Ahlfors, L., An extension of Schwarz’s lemma, Trans. Amer. Math. Soc. 43 (1938), 359–364.Google Scholar
Alvarez, A., Chaturvedi, A. and Heier, G., Optimal pinching for the holomorphic sectional curvature of Hitchin’s metrics on Hirzebruch surfaces, Contemp. Math. 654 (2015), 133–142.CrossRefGoogle Scholar
Andreotti, A. and Grauert, H., Théorème de finitude pour la cohomologie des espaces complexes, Bull. Soc. Math. France 90 (1962), 193–259.CrossRefGoogle Scholar
Aronszajin, N., A unique continuation theorem for solutions of elliptic partial differential equations or inequalities of second order, J. Math. Pures Appl. 36 (1957), 235–249.Google Scholar
Chaturvedi, A. and Heier, G., Hermitian metrics of positive holomorphic sectional curvature on fibrations, Preprint, 2017, arXiv:1707.03425v1.Google Scholar
Alvarez, A., Heier, G. and Zheng, F.-Y., On projectivized vector bundles and positive holomorphic sectional curvature, Proc. Amer. Math. Soc. 146 (2018), 2877–2882.CrossRefGoogle Scholar
Campana, F. and Păun, M., Foliations with positive slopes and birational stability of orbifold cotangent bundles, Preprint, 2015, arXiv:1508.02456.Google Scholar
Cao, X.-D. and Yang, B., A note on the almost one half holomorphic pinching, Preprint, 2017, arXiv:1709.02527.CrossRefGoogle Scholar
Chern, S. S., On the holomorphic mappings of hermitian manifolds of the same dimension, in Proceedings of Symposia in Pure Mathematics, vol. 11, pp. 157–170 (American Mathematical Society, Providence, RI, 1968).Google Scholar
Demailly, J.-P., Peternell, T. and Schneider, M., Pseudo-effective line bundles on compact Kähler manifolds, Internat. J. Math. 6 (2001), 689–741.CrossRefGoogle Scholar
Griffiths, P., Hermitian differential geometry, Chern classes and positive vector bundles, in Global Analysis, papers in honor of K. Kodaira, pp. 181–251 (Princeton University Press, Princeton, 1969).Google Scholar
Griffiths, P., Two theorems on extensions of holomorphic maps, Invent. Math. 14 (1971), 27–62.CrossRefGoogle Scholar
Hartshorne, R., Ample vector bundles, Publ. Math. Inst. Hautes Études Sci. 29 (1966), 319–350.CrossRefGoogle Scholar
Jost, J. and Yau, S.-T., A nonlinear elliptic system for maps from Hermitian to Riemannian manifolds and rigidity theorems in Hermitian geometry, Acta Math. 170(2) (1993), 221–254.CrossRefGoogle Scholar
Le Potier, J., Annulation de la cohomolgie à valeurs dans un fibré vectoriel holomorphe positif de rang quelconque. (French), Math. Ann. 218(1) (1975), 35–53.CrossRefGoogle Scholar
Liu, K.-F. and Yang, X.-K., Ricci curvatures on Hermitian manifolds, Trans. Amer. Math. Soc. 369 (2017), 5157–5196.CrossRefGoogle Scholar
Liu, G., Three-circle theorem and dimension estimate for holomorphic functions on Kähler manifolds, Duke Math. J. 165(15) (2016), 2899–2919.CrossRefGoogle Scholar
Lu, Y., Holomorphic mappings of complex manifolds, J. Differential Geom. 2 (1968), 299–312.CrossRefGoogle Scholar
Matsumura, S., On the image of MRC fibrations of projective manifolds with semi-positive holomorphic sectional curvature, Preprint, 2018, arXiv:1801.09081.Google Scholar
Ni, L., Vanishing theorems on complete Kähler manifolds and their applications, J. Differential Geom. 50(1) (1998), 89–122.Google Scholar
Ni, L. and Zheng, F.-Y., Comparison and vanishing theorems for Kähler manifolds, Preprint, 2018, arXiv:1802.08732.CrossRefGoogle Scholar
Ni, L. and Zheng, F.-Y., Positivity and Kodaira embedding theorem, Preprint, 2018, arXiv:1804.09696.Google Scholar
Păun, M., Singular Hermitian metrics and positivity of direct images of pluricanonical bundles, Preprint, 2016, arXiv:1606.00174.Google Scholar
Păun, M. and Takayama, S., Positivity of twisted relative pluricanonical bundles and their direct images, J. Algebraic Geom. 27 (2018), 211–272.CrossRefGoogle Scholar
Royden, H. L., The Ahlfors-Schwarz lemma in several complex variables, Comment. Math. Helv. 55(4) (1980), 547–558.CrossRefGoogle Scholar
Shiffman, B., Extension of holomorphic maps into hermitian manifolds, Math. Ann. 194 (1971), 249–258.CrossRefGoogle Scholar
Shiffman, B. and Sommese, A. J., Vanishing theorems on complex manifolds, in Progress in Mathematics, 56 (Birkhauser Boston, Inc., Boston, MA, 1985).Google Scholar
Siu, Y.-T., The complex-analyticity of harmonic maps and the strong rigidity of compact Kähler manifolds, Ann. of Math. (2) 112(1) (1980), 73–111.CrossRefGoogle Scholar
Tossati, V., A general Schwarz lemma for almost-Hermitian manifolds, Comm. Anal. Geom. 15(5) (2007), 1063–1086.CrossRefGoogle Scholar
Yang, B. and Zheng, F.-Y., Hirzebruch manifolds and positive holomorphic sectional curvature, Preprint, 2016, arXiv:1611.06571v2.Google Scholar
Yang, X.-K., Hermitian manifolds with semi-positive holomorphic sectional curvature, Math. Res. Lett. 23(3) (2016), 939–952.CrossRefGoogle Scholar
Yang, X.-K., A partial converse to the Andreotti-Grauert theorem, Compos. Math. 155(1) (2019), 89–99.CrossRefGoogle Scholar
Yang, X.-K., RC-positivity, rational connectedness and Yau’s conjecture, Camb. J. Math. 6 (2018), 183–212.CrossRefGoogle Scholar
Yang, X.-K., RC-positive metrics on rationally connected manifolds, Preprint, 2018, arXiv:1807.03510.Google Scholar
Yang, X.-K., RC-positivity and the generalized energy density I: rigidity, Preprint, 2018, arXiv:1810.03276.Google Scholar
Yang, X.-K., Rigidity theorems on complete Kähler manifolds with RC-positive curvature (in preparation).Google Scholar
Yang, X.-K. and Zheng, F.-Y., On real bisectional curvature for Hermitian manifolds, Trans. Amer. Math. Soc. 371(4) (2019), 2703–2718.CrossRefGoogle Scholar
Yau, S.-T., Harmonic functions on complete Riemannian manifolds, Comm. Pure Appl. Math. 28 (1975), 201–228.CrossRefGoogle Scholar
Yau, S.-T., A general Schwarz lemma for Kähler manifolds, Amer. J. Math. 100(1) (1978), 197–203.CrossRefGoogle Scholar
Yau, S.-T., On the Ricci curvature of a compact Kähler manifold and the complex Monge-Ampère equation, I, Comm. Pure Appl. Math. 31 (1978), 339–411.CrossRefGoogle Scholar
Yau, S.-T., Problem section. In Seminar on Differential Geometry, Ann. of Math Stud. 102 (1982), 669–706.Google Scholar