Hostname: page-component-6bf8c574d5-k2jvg Total loading time: 0 Render date: 2025-03-09T23:04:57.090Z Has data issue: false hasContentIssue false
  • English
  • Français

SERRE WEIGHTS FOR LOCALLY REDUCIBLE TWO-DIMENSIONAL GALOIS REPRESENTATIONS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  23 May 2014

Fred Diamond  and
David Savitt
Fred Diamond
Affiliation:
Department of Mathematics, King’s College London, UK (fred.diamond@kcl.ac.uk)
David Savitt
Affiliation:
Department of Mathematics, University of Arizona, USA (savitt@math.arizona.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $F$ be a totally real field, and $v$ a place of $F$ dividing an odd prime 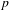$p$. We study the weight part of Serre’s conjecture for continuous totally odd representations 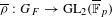$\overline{{\it\rho}}:G_{F}\rightarrow \text{GL}_{2}(\overline{\mathbb{F}}_{p})$ that are reducible locally at $v$. Let 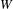$W$ be the set of predicted Serre weights for the semisimplification of 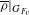$\overline{{\it\rho}}|_{G_{F_{v}}}$. We prove that, when 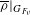$\overline{{\it\rho}}|_{G_{F_{v}}}$ is generic, the Serre weights in 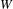$W$ for which 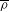$\overline{{\it\rho}}$ is modular are exactly the ones that are predicted (assuming that 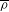$\overline{{\it\rho}}$ is modular). We also determine precisely which subsets of 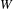$W$ arise as predicted weights when 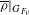$\overline{{\it\rho}}|_{G_{F_{v}}}$ varies with fixed generic semisimplification.

Keywords

Galois representationsSerre’s conjectureBreuil modules

MSC classification

Primary: 11F80: Galois representations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 14 , Issue 3 , July 2015 , pp. 639 - 672
Copyright
© Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barnet-Lamb, T., Gee, T. and Geraghty, D., Serre weights for rank two unitary groups, Math. Ann. (2013), to appear.Google Scholar
Breuil, C., Groupes p-divisibles, groupes finis et modules filtrés, Ann. of Math. (2) 152(2) (2000), 489–549.Google Scholar
Breuil, C., Conrad, B., Diamond, F. and Taylor, R., On the modularity of elliptic curves over Q, J. Amer. Math. Soc. 14 (2001), 843–939.CrossRefGoogle Scholar
Breuil, C. and Paškūnas, V., Towards a modulo p Langlands correspondence for GL2, Mem. Amer. Math. Soc. 216(1016) (2012), vi+114.Google Scholar
Buzzard, K., Diamond, F. and Jarvis, F., On Serre’s conjecture for mod l Galois representations over totally real fields, Duke Math. J. 155(1) (2010), 105–161.CrossRefGoogle Scholar
Caruso, X., Schémas en groupes et poids de Diamond–Serre (arXiv:0705.1213).Google Scholar
Caruso, X. and Liu, T., Quasi-semi-stable representations, Bull. Soc. Math. France 137(2) (2009), 185–223.CrossRefGoogle Scholar
Chang, S. and Diamond, F., Extensions of rank one (𝜑, Γ)-modules and crystalline representations, Compos. Math. 147(2) (2011), 375–427.Google Scholar
Cheng, C., Rank two Breuil modules: basic structures, J. Number Theory 132(11) (2012), 2379–2396.Google Scholar
Conrad, B., Lifting global representations with local properties, preprint, 2011.Google Scholar
Diamond, F., A correspondence between representations of local Galois groups and Lie-type groups, in L-functions and Galois representations, pp. 187–206 (Cambridge University Press, Cambridge, 2007).Google Scholar
Edixhoven, B., The weight in Serre’s conjectures on modular forms, Invent. Math. 109(3) (1992), 563–594.Google Scholar
Emerton, M., Gee, T., Herzig, F. and Savitt, D., General Serre weight conjectures, in preparation, 2013.Google Scholar
Gee, T., Automorphic lifts of prescribed types, Math. Ann. 350(1) (2011), 107–144.Google Scholar
Gee, T., On the weights of mod p Hilbert modular forms, Invent. Math. 184 (2011), 1–46 (10.1007/s00222-010-0284-5).Google Scholar
Gee, T. and Kisin, M., The Breuil–Mézard Conjecture for potentially Barsotti–Tate representations (http://arxiv.org/abs/1208.3179).Google Scholar
Gee, T., Liu, T. and Savitt, D., The Buzzard-Diamond-Jarvis conjecture for unitary groups, J. Amer. Math. Soc. 27(2) (2014), 389–435.Google Scholar
Gee, T., Liu, T. and Savitt, D., Crystalline extensions and the weight part of Serre’s conjecture, Algebra Number Theory 6(7) (2012), 1537–1559.Google Scholar
Gee, T., Liu, T. and Savitt, D., The weight part of serre’s conjecture for $\text{GL}(2)$, preprint, 2013.Google Scholar
Gee, T. and Savitt, D., Serre weights for mod p Hilbert modular forms: the totally ramified case, J. Reine Angew. Math. 660 (2011), 1–26.Google Scholar
Gee, T. and Savitt, D., Serre weights for quaternion algebras, Compos. Math. 147(4) (2011), 1059–1086.CrossRefGoogle Scholar
Kisin, M., Potentially semi-stable deformation rings, J. Amer. Math. Soc. 21(2) (2008), 513–546.CrossRefGoogle Scholar
Nekovář, J., On p-adic height pairings, in Séminaire de théorie des nombres, (Paris, 1990–91), Progress in Mathematics, Volume 108, pp. 127–202 (Birkhäuser Boston, Boston, MA, 1993).Google Scholar
Raynaud, M., Schémas en groupes de type (p, p, …, p), Bull. Soc. Math. France 102 (1974), 241–280.CrossRefGoogle Scholar
Savitt, D., Modularity of some potentially Barsotti–Tate Galois representations, Compos. Math. 140(1) (2004), 31–63.Google Scholar
Savitt, D., On a conjecture of Conrad, Diamond, and Taylor, Duke Math. J. 128(1) (2005), 141–197.Google Scholar
Savitt, D., Breuil modules for Raynaud schemes, J. Number Theory 128 (2008), 2939–2950.Google Scholar
Schein, M. M., Weights in Serre’s conjecture for Hilbert modular forms: the ramified case, Israel J. Math. 166 (2008), 369–391.CrossRefGoogle Scholar
Schein, M. M., Reduction modulo p of cuspidal representations and weights in Serre’s conjecture, Bull. Lond. Math. Soc. 41(1) (2009), 147–154.Google Scholar
Smith, R., Serre weights: the partially ramified case, PhD thesis, University of Arizona (2012).Google Scholar