Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T04:06:31.063Z Has data issue: false hasContentIssue false
  • English
  • Français

SPECIAL VALUES OF THE ZETA FUNCTION OF AN ARITHMETIC SURFACE

Part of: Arithmetic algebraic geometry (Co)homology theory

Published online by Cambridge University Press:  15 March 2021

Matthias Flach Open the ORCID record for Matthias Flach [Opens in a new window]  and
Daniel Siebel
Matthias Flach
Affiliation:
Dept. of Mathematics 253-37, California Institute of Technology, PasadenaCA91125 (flach@caltech.edu, daniel.siebel@yahoo.de)
Daniel Siebel
Affiliation:
Dept. of Mathematics 253-37, California Institute of Technology, PasadenaCA91125 (flach@caltech.edu, daniel.siebel@yahoo.de)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that the special-value conjecture for the zeta function of a proper, regular, flat arithmetic surface formulated in [6] at 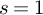$s=1$ is equivalent to the Birch and Swinnerton-Dyer conjecture for the Jacobian of the generic fibre. There are two key results in the proof. The first is the triviality of the correction factor of [6, Conjecture 5.12], which we show for arbitrary regular proper arithmetic schemes. In the proof we need to develop some results for the eh-topology on schemes over finite fields which might be of independent interest. The second result is a different proof of a formula due to Geisser, relating the cardinalities of the Brauer and the Tate–Shafarevich group, which applies to arbitrary rather than only totally imaginary base fields.

Keywords

arithmetic surfaceszeta valuesWeil-étale cohomologyBirch and Swinnerton-Dyer conjecture

MSC classification

Primary: 14F20: Étale and other Grothendieck topologies and (co)homologies
Secondary: 14F42: Motivic cohomology; motivic homotopy theory 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 6 , November 2022 , pp. 2043 - 2091
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Beilinson, A., Bernstein, J. and Deligne, P., Faisceaux pervers: Analyse et topologie sur les éspaces singuliers, Astérisque, 100 (Société Mathématique de France, Paris, 1982).Google Scholar
Bloch, S., De Rham cohomology and conductors of curves, Duke Math. J. 54(2) (1987), 295–308.CrossRefGoogle Scholar
Bosch, S. and Liu, Q., Rational points of the group of components of a Neron model, Manuscripta Math. 98(3) (1999), 275–293.CrossRefGoogle Scholar
Colliot-Thélène, J. L. and Saito, S., Zéro-cycles sur les variétés p-adiques et groupe de Brauer, Int. Math. Res. Not. IMRN 4 (1996), 151–160.CrossRefGoogle Scholar
Conrad, B., ‘Seminar notes on the Birch and Swinnerton-Dyer conjecture’, 2015, http://virtualmath1.stanford.edu/conrad/BSDseminar/.Google Scholar
Flach, M. and Morin, B., Weil-étale cohomology and Zeta-values of proper regular arithmetic schemes, Doc. Math. 23 (2018), 1425–1560.Google Scholar
Flach, M. and Morin, B., Deninger’s conjectures and Weil-Arakelov cohomology, Münster J. Math., 13(2) (2020), 519–540.Google Scholar
Fujiwara, K., A proof of the absolute purity conjecture (after Gabber), in Algebraic Geometry 2000, Azumino (Hotaka), Advanced Studies in Pure Mathematics, 36 pp. 153–183 (Mathematical Society of Japan, Tokyo, 2002).CrossRefGoogle Scholar
Geisser, T., Arithmetic cohomology over finite fields and special values of $\zeta$ -functions, Duke Math. Jour. 133(1) (2006), 27–57.CrossRefGoogle Scholar
Geisser, T., Comparing the Brauer to the Tate-Shafarevich group, J. Inst. Math. Jussieu, 19(3) (2020), 965–970.CrossRefGoogle Scholar
Gordon, W. J., Linking the conjectures of Artin-Tate and Birch-Swinnerton-Dyer, Compos. Math. 38(2) (1979), 163–199.Google Scholar
Gross, B. H. and Harris, J., Real algebraic curves, Ann. Sci. Éc. Norm. Supér. (4) 14 (1981), 157–182.CrossRefGoogle Scholar
Grothendieck, A., Techniques de descente et théorèmes d’existence en géométrie algébrique VI, in Les schémas de Picard: propriétés générales, Séminaire Bourbaki, 236, pp. 221–243 (Société Mathématique de France, Paris, 1962).Google Scholar
Grothendieck, A., Le groupe de Brauer III: Dix exposés sur la cohomologie des schémas (North Holland, Amsterdam, 1968).Google Scholar
Grothendieck, A., Revétements étales et groupe fondamental (SGA 1), Lecture Notes in Mathematics, 224 (Springer, Berlin-Heidelberg, 1971).CrossRefGoogle Scholar
Grothendieck, A., Artin, M. and Verdier, J. L., Theorie des Topos et Cohomologie Etale des Schemas (SGA 4), Lecture Notes in Mathematics 269, 270, 271 (Springer, Berlin-Heidelberg, 1972).CrossRefGoogle Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics, 52 (Springer, New-York, 1977).CrossRefGoogle Scholar
Hindry, S. and Silverman, J., Diophantine Geometry: An Introduction, Graduate Text in Mathematics, 201 (Springer, New-York, 2000).CrossRefGoogle Scholar
Hriljac, P., Heights and Arakelov’s intersection theory, Amer. J. Math. 107(1) (1985), 23–38.CrossRefGoogle Scholar
Illusie, L., Complexe cotangent et déformations. I, Lecture Notes in Mathematics, 239 (Springer, Berlin-Heidelberg, 1971).CrossRefGoogle Scholar
Li, y., Liu, Y. and Tian, Y., ‘On the Birch and Swinnerton-Dyer conjecture for CM elliptic curves over $\mathbb{Q}$ ’, Preprint, 2016, https://arxiv.org/abs/1605.01481v1.Google Scholar
Lichtenbaum, S., Duality theorems for curves over $p$ -adic fields, Invent. Math. 7 (1969), 120–136.CrossRefGoogle Scholar
Liu, Q., Lorenzini, D. and Raynaud, M., Néron models, Lie algebras, and reduction of curves of genus one, Invent. Math. 157 (2004), 455–518.CrossRefGoogle Scholar
Liu, Q., Lorenzini, D. and Raynaud, M., Corrigendum to Néron models, Lie algebras, and reduction of curves of genus one and The Brauer group of a surface, Invent. Math. 214 (2018), 593–604.CrossRefGoogle Scholar
Lurie, J., Higher Algebra, 2017, http://www.math.ias.edu/lurie/papers/HA.pdf.Google Scholar
Milne, J.S., Étale Cohomology, Princeton Mathematical Series, 17 (Princeton University Press, Princeton N.J., 1980).Google Scholar
Milne, J.S., Arithmetic Duality Theorems, Perspectives in Mathematics, 1 (Academic Press, Boston, 1986).Google Scholar
Poonen, B. and Stoll, M., The Cassels-Tate pairing on polarized abelian varieties, Annals of Math. 150 (1999), 1109–1149.CrossRefGoogle Scholar
Raynaud, M., Spécialisation du foncteur du Picard, Publ. Math. Inst. Hautes Études Sci. 38 (1970), 27–76.CrossRefGoogle Scholar
Saito, S., Arithmetic theory of arithmetic surfaces, Ann. Math. 129 (1989), 547–589.CrossRefGoogle Scholar
Sato, K., $p$ -adic étale twists and arithmetic duality, Ann. Sci. Éc. Norm. Supér. (4) 40(4) (2007), 519–588.CrossRefGoogle Scholar
Soulé, C., Abramovich, D., Burnol, J.-F. and Kramer, J., Lectures on Arakelov Geometry, (Cambridge University Press, Cambridge U.K., 1992).CrossRefGoogle Scholar
Spiess, M., Artin-Verdier duality for arithmetic surfaces, Math. Ann. 305 (1996), 705–792.CrossRefGoogle Scholar
The Stacks Project Authors, The Stacks Project, 2019, http://stacks.math.columbia.edu.Google Scholar
Tate, J., On the conjecture of Birch and Swinnerton-Dyer and a geometric analogue, Sém. Bourbaki, 306, pp. 1–26 (Société Mathématique de France, Paris, 1966).Google Scholar
Voevodsky, V., Homology of schemes, Selecta Math. (N. S.) 2(1) (1996), 111–153.CrossRefGoogle Scholar
Wan, X., ‘Iwasawa main conjecture for supersingular elliptic curves and BSD conjecture’, Preprint, 2019, https://arXiv.org/abs/1411.6352v6.Google Scholar
Zhong, C., Comparison of dualizing complexes, J. Reine Angew. Math. 695 (2014), 1–39.CrossRefGoogle Scholar