Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-11T09:17:26.890Z Has data issue: false hasContentIssue false
  • English
  • Français

STABLE SETS OF CERTAIN NON-UNIFORMLY HYPERBOLIC HORSESHOES HAVE THE EXPECTED DIMENSION

Part of: Low-dimensional dynamical systems Measure-theoretic ergodic theory Smooth dynamical systems: general theory

Published online by Cambridge University Press:  04 April 2019

Carlos Matheus ,
Jacob Palis  and
Jean-Christophe Yoccoz
Carlos Matheus
Affiliation:
Université Paris 13, Sorbonne Paris Cité, LAGA, CNRS (UMR 7539), F-93439, Villetaneuse, France (matheus@impa.br)
Jacob Palis
Affiliation:
IMPA, Estrada D. Castorina, 110, CEP 22460-320, Rio de Janeiro, RJ, Brazil (jpalis@impa.br)
Jean-Christophe Yoccoz
Affiliation:
Collège de France, 3, Rue d’Ulm, Paris, CEDEX 05, France (jean-c.yoccoz@college-de-france.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the stable and unstable sets of non-uniformly hyperbolic horseshoes arising in some heteroclinic bifurcations of surface diffeomorphisms have the value conjectured in a previous work by the second and third authors of the present paper. Our results apply to first heteroclinic bifurcations associated with horseshoes with Hausdorff dimension 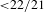${<}22/21$ of conservative surface diffeomorphisms.

Keywords

heteroclinic bifurcationsnon-uniformly hyperbolic horseshoesHausdorff dimension

MSC classification

Primary: 37C29: Homoclinic and heteroclinic orbits 37E30: Homeomorphisms and diffeomorphisms of planes and surfaces
Secondary: 28D20: Entropy and other invariants
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 1 , January 2021 , pp. 305 - 329
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A. and Bochi, J., A generic C 1 map has no absolutely continuous invariant probability measure, Nonlinearity 19 (2006), 2717–2725.CrossRefGoogle Scholar
Matheus, C., Moreira, C. G. and Palis, J., Non-uniformly hyperbolic horseshoes in the standard family, C. R. Math. Acad. Sci. Paris 356 (2018), 146–149.CrossRefGoogle Scholar
Matheus, C. and Palis, J., An estimate on the Hausdorff dimension of stable sets of non-uniformly hyperbolic horseshoes, Discrete Contin. Dyn. Syst. 38 (2018), 431–448.CrossRefGoogle Scholar
Matheus, C., Palis, J. and Yoccoz, J.-C., The Hausdorff dimension of stable sets of non-uniformly hyperbolic horseshoes, work in progress.Google Scholar
Palis, J. and Yoccoz, J.-C., Non-uniformly hyperbolic horseshoes arising from bifurcations of Poincaré heteroclinic cycles, Publ. Math. Inst. Hautes Études Sci. 110 (2009), 1–217.CrossRefGoogle Scholar