Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T15:54:13.416Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur la conjecture de Manin pour certaines surfaces de Châtelet

Part of: Diophantine equations

Published online by Cambridge University Press:  08 March 2013

Régis de la Bretèche  and
Gérald Tenenbaum
Régis de la Bretèche
Affiliation:
Institut de Mathématiques de Jussieu, UMR 7586, Université Paris Diderot-Paris 7, UPR de Mathématiques, case 7012, Bâtiment Chevaleret, 75205 Paris Cedex 13, France (breteche@math.jussieu.fr)
Gérald Tenenbaum
Affiliation:
Institut Élie Cartan, Université de Lorraine, BP 70239, 54506 Vandœuvre-lès-Nancy Cedex, France (gerald.tenenbaum@univ-lorraine.fr)
Get access Rights & Permissions [Opens in a new window]

Résumé

Nous démontrons, sous la forme forte conjecturée par Peyre, la conjecture de Manin pour les surfaces de Châtelet dont les équations sont du type 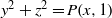${y}^{2} + {z}^{2} = P(x, 1)$, où 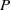$P$ est une forme binaire quartique à coefficients entiers irréductible sur 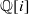$ \mathbb{Q} [i] $ ou produit de deux formes quadratiques à coefficients entiers irréductibles sur 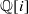$ \mathbb{Q} [i] $. De plus, nous fournissons une estimation explicite du terme d’erreur de la formule asymptotique sous-jacente. Cela finalise essentiellement la validation de la conjecture de Manin pour l’ensemble des surfaces de Châtelet. La preuve s’appuie sur deux méthodes nouvelles, concernant, du part, les estimations en moyenne d’oscillations locales de caractères sur les diviseurs, et, d’autre part, les majorations de certaines fonctions arithmétiques de formes binaires.

Abstract

We prove Manin’s conjecture, in the strong form conjectured by Peyre, for Châtelet surfaces associated to surfaces of the type 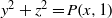${y}^{2} + {z}^{2} = P(x, 1)$, where 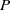$P$ is a binary quartic form with integer coefficients that is either irreducible over 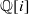$ \mathbb{Q} [i] $ or the product of two quadratic forms with integer coefficients and irreducible over 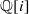$ \mathbb{Q} [i] $. Moreover, we provide an explicit upper bound for the remainder term in the relevant asymptotic formula. This essentially settles Manin’s conjecture for all Châtelet surfaces. The proof rests on two new tools, namely upper bounds for mean values of local oscillations of characters on divisors and sharp upper estimates for mean values of arithmetic functions of binary forms.

Keywords

Châtelet surfacesManin’s conjecturePeyre’s constantdel Pezzo surfaces of degree 4count of lattice points over algebraic varietiesnumber of representations as a sum of two squaresmethod of descent

MSC classification

Secondary: 11D45: Counting solutions of Diophantine equations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 4 , October 2013 , pp. 759 - 819
Copyright
©Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bibliographie

de la Bretèche, R. et Browning, T. D., Sums of arithmetic functions over values of binary forms, Acta Arith. 125 (3) (2006), 291–304.Google Scholar
de la Bretèche, R. et Browning, T. D., Binary linear forms as sums of two squares, Compositio Math. 144 (6) (2008), 1375–1402.CrossRefGoogle Scholar
de la Bretèche, R. et Browning, T. D., Le problème des diviseurs pour des formes binaires de degré 4, J. Reine Angew. Math. 646 (2010), 1–44.CrossRefGoogle Scholar
de la Bretèche, R. et Browning, T. D., Binary forms of two squares and Châtelet surfaces, Israel J. Math. 191 (2012), 973–1012.CrossRefGoogle Scholar
de la Bretèche, R., Browning, T. D. et Peyre, E., On Manin’s conjecture for a family of Châtelet surfaces, Ann. of Math. 175 (2012), 1–47.CrossRefGoogle Scholar
de la Bretèche, R. et Tenenbaum, G., Oscillations localisées sur les diviseurs, J. Lond. Math. Soc. 85 (3) (2012), 669–693.CrossRefGoogle Scholar
de la Bretèche, R. et Tenenbaum, G., Moyennes de fonctions arithmétiques de formes binaires, Mathematika 58 (2012), 290–304.CrossRefGoogle Scholar
Browning, T. D., Quantitative arithmetic of projective varieties, Prog. Math., Volume 277 (Birkhäuser, 2009).Google Scholar
Browning, T. D., Linear growth for Châtelet surfaces, Math. Ann. 346 (2010), 41–50.Google Scholar
Colliot-Thélène, J.-L., Coray, D. et Sansuc, J.-J., Descente et principe de Hasse pour certaines variétés rationnelles, J. Reine Angew. Math. 320 (1980), 150–191.Google Scholar
Colliot-Thélène, J.-L. et Sansuc, J.-J., La descente sur les variétés rationnelles, Journées de géométrie algébrique d’Angers (1979) (ed. Beauville, A.), pp. 223–237 (Sijthoff & Noordhoff, Alphen aan den Rijn, 1980).Google Scholar
Colliot-Thélène, J.-L., Sansuc, J.-J. et Swinnerton-Dyer, P., Intersections of two quadrics and Châtelet surfaces. I, J. Reine Angew. Math. 373 (1987), 37–107.Google Scholar
Colliot-Thélène, J.-L., Sansuc, J.-J. et Swinnerton-Dyer, P., Intersections of two quadrics and Châtelet surfaces. II, J. Reine Angew. Math. 374 (1987), 72–168.Google Scholar
Cook, R. J., Simultaneous quadratic equations, J. Lond. Math. Soc. 4 (2) (1971), 319–326.Google Scholar
Daniel, S., On the divisor-sum problem for binary forms, J. Reine Angew. Math. 507 (1999), 107–129.Google Scholar
Derenthal, U., On a constant arising in Manin’s conjecture for del Pezzo surfaces, Math. Res. Lett. 14 (3) (2007), 481–489.Google Scholar
Hall, R. R. et Tenenbaum, G., Divisors, Cambridge tracts in mathematics, Volume 90, Cambridge University Press (1988, paperback ed. 2008).Google Scholar
Heath-Brown, D. R., Diophantine approximation with square-free numbers, Math. Z. 187 (1984), 335–344.CrossRefGoogle Scholar
Heath-Brown, D. R., Linear relations amongst sums of two squares, in Number theory and algebraic geometry, London Math. Soc. Lecture Note Ser., Volume 303, pp. 133–176 (CUP, 2003).Google Scholar
Heilbronn, H., Zeta-functions and $L$-functions, in Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965), pp. 204–230 (Thompson, Washington, D.C, 1967).Google Scholar
Henriot, K., Nair–Tenenbaum bounds uniform with respect to the discriminant, Math. Proc. Cambridge Philos. Soc. 152 (2012), 405–424.Google Scholar
Hooley, C., A new technique and its applications to the theory of numbers, Proc. Lond. Math. Soc. 38 (3) (1979), 115–151.Google Scholar
Iskovskih, V. A., A counterexample to the Hasse principle for systems of two quadratic forms in five variables, Mat. Z. 10 (1971), 253–257, English transl. in Math. Notes 10 (1971), 575–577.Google Scholar
Maier, H. et Tenenbaum, G., On the normal concentration of divisors, 2, Math. Proc. Cambridge Philos. Soc. 147 (3) (2009), 593–614.Google Scholar
Marasingha, G., On the representation of almost primes by pairs of quadratic forms, Acta Arith. 124 (4) (2006), 327–355.CrossRefGoogle Scholar
Nagell, T., Introduction to number theory, 2nd edn (Chelsea, 1964).Google Scholar
Peyre, E., Hauteurs et mesures de Tamagawa sur les variétés de Fano, Duke Math. J. 79 (1995), 101–218.Google Scholar
Peyre, E., Points de hauteur bornée, topologie adélique et mesures de Tamagawa, J. Théor. Nombres Bordeaux 15 (1) (2003), 319–349.Google Scholar
Skorobogatov, A., Torsors and rational points, Cambridge Tracts in Mathematics, Volume 144 (Cambridge University Press, Cambridge, 2001), viii+187 pp.Google Scholar
Stewart, C. L., On the number of solutions of polynomial congruences and Thue equations, J. Amer. Math. Soc. 4 (1991), 793–835.Google Scholar
Tenenbaum, G., Sur une question d’Erdős et Schinzel, II, Invent. Math. 99 (1990), 215–224.CrossRefGoogle Scholar
Tenenbaum, G., Introduction à la théorie analytique et probabiliste des nombres, troisième édition, Belin (coll. Échelles, 2008), 592 pp.Google Scholar