Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T14:26:39.199Z Has data issue: false hasContentIssue false
  • English
  • Français

TEMPERED SPECTRAL TRANSFER IN THE TWISTED ENDOSCOPY OF REAL GROUPS

Part of: Lie groups Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  17 December 2014

Paul Mezo
Paul Mezo*
Affiliation:
The School of Mathematics and Statistics, Carleton University, Ottawa, ON, Canada (mezo@math.carleton.ca)
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that 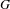$G$ is a connected reductive algebraic group defined over 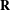$\mathbf{R}$, 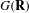$G(\mathbf{R})$ is its group of real points, 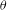${\it\theta}$ is an automorphism of 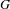$G$, and ${\it\omega}$ is a quasicharacter of 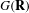$G(\mathbf{R})$. Kottwitz and Shelstad defined endoscopic data associated to 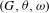$(G,{\it\theta},{\it\omega})$, and conjectured a matching of orbital integrals between functions on 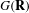$G(\mathbf{R})$ and its endoscopic groups. This matching has been proved by Shelstad, and it yields a dual map on stable distributions. We express the values of this dual map on stable tempered characters as a linear combination of twisted characters, under some additional hypotheses on 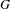$G$ and 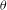${\it\theta}$.

Keywords

twisted endoscopyspectral transfer

MSC classification

Primary: 22E45: Representations of Lie and linear algebraic groups over real fields
Secondary: 22E47: Representations of Lie and real algebraic groups 11S37: Langlands-Weil conjectures, nonabelian class field theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 15 , Issue 3 , July 2016 , pp. 569 - 612
Copyright
© Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arthur, J., The Endoscopic Classification of Representations: Orthogonal and Symplectic Groups (American Mathematical Society, 2013).Google Scholar
Arthur, J., The local behaviour of weighted orbital integrals, Duke Math. J. 56 (1988), 223–293.CrossRefGoogle Scholar
Arthur, J., Problems for real groups, in Representation Theory of Real Reductive Lie Groups, Contemporary Mathematics, Volume 472, pp. 39–62 (2008).Google Scholar
Borel, A., Automorphic L-functions, in Automorphic Forms, Representations, and L-functions, Proc. Sympos. Pure Math., Volume 33, pp. 27–61 (1979).CrossRefGoogle Scholar
Borel, A., Linear Algebraic Groups (Springer, 1991).Google Scholar
Bouaziz, A., Sur les caractères des groupes de Lie réductifs non connexes, J. Funct. Anal. 70 (1987), 1–79.Google Scholar
Bouaziz, A., Relèvement des caractères d’un groupe endoscopique pour le changement de base C/R, in Orbites Unipotentes et Représentations, number 171–172 in Astérisque, pp. 163–194 (Société Mathématique de France, 1989).Google Scholar
Bouaziz, A., Intégrales orbitales sur les groupes de Lie réductifs, Ann. Sci. Éc. Norm. Supér. 27 (1994), 573–609.Google Scholar
Chenevier, G. and Clozel, L., Corps de nombres peu ramifiés et formes automorphes autoduales, J. Amer. Math. Soc. 22 (2009), 467–519.Google Scholar
Clozel, L., Changement de base pour les représentations tempérées des groupes réductifs réels, Ann. Sci. Éc. Norm. Supér. 15 (1982), 45–115.Google Scholar
Clozel, L., Identités de caractères en la place archimédienne, in On the Stabilization of the Trace Formula, Vol. 1, (ed. Labesse, J.-P., Clozel, L., Harris, M. and Ngô, B.-C.), pp. 351–367 (International Press, 2011).Google Scholar
Delorme, P. and Mezo, P., A twisted invariant Paley–Wiener theorem for real reductive groups, Duke Math. J. 144 (2008), 341–380.Google Scholar
Duflo, M., Construction de représentations unitaires d’un groupe de Lie, in Harmonic Analysis an Group Representations, pp. 129–221 (Liguori, 1982).Google Scholar
Harish-Chandra, Discrete series for semisimple Lie groups II, Acta Math. 116 (1966), 1–111.Google Scholar
Horváth, J., Topological Vector Spaces and Distributions (Addison-Wesley, 1966).Google Scholar
Humphreys, J. E., Introduction to Lie Algebras and Representation Theory (Springer, 1994).Google Scholar
Knapp, A. W., Representation Theory of Semisimple Groups (Princeton University Press, 1986).Google Scholar
Knapp, A. W., Lie Groups Beyond and Introduction (Birkhäuser, 1996).Google Scholar
Kottwitz, R., Stable trace formula: elliptic singular terms, Math. Ann. 275 (1986), 365–399.Google Scholar
Kottwitz, R. E. and Shelstad, D., Foundations of twisted endoscopy, Astérisque 255 (1999).Google Scholar
Knapp, A. W. and Zuckerman, G., Normalizing factors, tempered representations, and l-groups, in Automorphic Forms, Representations, and L-functions, Proc. Sympos. Pure Math., Volume 33, pp. 93–106 (1979).Google Scholar
Knapp, A. W. and Zuckerman, G., Classification of irreducible tempered representations of semisimple groups, Ann. of Math. (2) 116 (1984), 389–501.Google Scholar
Labesse, J.-P., Stable twisted trace formula: elliptic terms, J. Inst. Math. Jussieu 3 (2004), 473–530.CrossRefGoogle Scholar
Labesse, J.-P., Introduction to endoscopy, in Representation Theory of Real Reductive Groups, Contemporary Mathematics, Volume 472, pp. 175–213 (2008).Google Scholar
Langlands, R. P., Stable conjugacy: definitions and lemmas, Canad. J. Math. 31 (1979), 700–725.CrossRefGoogle Scholar
Langlands, R. P., On the classification of irreducible representations of real algebraic groups, in Representation Theory and Harmonic Analysis on Semisimple Lie groups, Mathematical Surveys and Monographs, Volume 31, pp. 101–170 (American Mathematical Society, 1989).Google Scholar
Mezo, P., Automorphism-invariant representations of real reductive groups, Amer. J. Math. 129 (2007), 1063–1085.Google Scholar
Mezo, P., Character identities in the twisted endoscopy of real reductive groups, Mem. Amer. Math. Soc. 222(1042) (2013).Google Scholar
Renard, D., Intégrales orbitales tordues sur les groupes de Lie réductifs réels, J. Funct. Anal. 145 (1997), 374–454.Google Scholar
Schwartz, L., Théorie des Distributions (Hermann, 1957).Google Scholar
Shelstad, D., On spectral transfer factors in real twisted endoscopy. See http://andromeda.rutgers.edu/∼shelstad.Google Scholar
Shelstad, D., Embeddings of L-groups, Canad. J. Math. 33 (1981), 513–558.Google Scholar
Shelstad, D., L-indistinguishability for real groups, Math. Ann. 259 (1982), 385–430.Google Scholar
Shelstad, D., Tempered endoscopy for real groups I. Geometric transfer with canonical factors, in Representation Theory of Real Reductive Groups, Contemporary Mathematics, Volume 472, pp. 215–246 (2008).Google Scholar
Shelstad, D., Tempered endoscopy for real groups. III. Inversion of transfer and L-packet structure, Represent. Theory 12 (2008), 369–402.Google Scholar
Shelstad, D., Tempered endoscopy for real groups II. Spectral transfer factors, in Automorphic Forms and the Langlands Program, Advanced Lectures in Mathematics, Volume 9, pp. 236–276 (2010).Google Scholar
Shelstad, D., On geometric transfer in real twisted endoscopy, Ann. of Math. (2) 176 (2012), 1919–1985.Google Scholar
Springer, T. A., Reductive groups, in Automorphic Forms, Representations, and L-functions, Proc. Sympos. Pure Math., Volume 33, pp. 3–27 (1979).CrossRefGoogle Scholar
Springer, T. A., Linear Algebraic Groups (Birkhäuser, 1998).Google Scholar
Steinberg, R., Endomorphisms of Linear Algebraic Groups, Collected Works (American Mathematical Society, 1997).Google Scholar
Speh, B. and Vogan, D. A., Reducibility of generalized principal series representations, Acta Math. 145 (1980), 227–299.CrossRefGoogle Scholar
Varadarajan, V. S., Harmonic Analysis on Real Reductive Groups, Lecture Notes in Mathematics, Volume 576 (Springer, 1977).Google Scholar
Vogan, D. A., Irreducible characters of semisimple Lie groups. IV, Duke Math. J. 49 (1982), 943–1073.CrossRefGoogle Scholar
Wallach, N., Real Reductive Groups I (Academic, 1988).Google Scholar
Waldspurger, J.-L., Préparation à la stabilisation de la formule des traces tordue III: intégrales orbitales et endoscopie sur un corps local archimédien. Preprint, May 2013.Google Scholar