Article contents
Topological flatness of local models for ramified unitary groups. II. The even dimensional case
Published online by Cambridge University Press: 10 July 2013
Abstract
Local models are schemes, defined in terms of linear-algebraic moduli problems, which are used to model the étale-local structure of integral models of certain 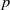 $p$ -adic PEL Shimura varieties defined by Rapoport and Zink. In the case of a unitary similitude group whose localization at
$p$ -adic PEL Shimura varieties defined by Rapoport and Zink. In the case of a unitary similitude group whose localization at 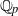 ${ \mathbb{Q} }_{p} $ is ramified, quasi-split
${ \mathbb{Q} }_{p} $ is ramified, quasi-split 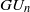 $G{U}_{n} $ , Pappas has observed that the original local models are typically not flat, and he and Rapoport have introduced new conditions to the original moduli problem which they conjecture to yield a flat scheme. In a previous paper, we proved that their new local models are topologically flat when
$G{U}_{n} $ , Pappas has observed that the original local models are typically not flat, and he and Rapoport have introduced new conditions to the original moduli problem which they conjecture to yield a flat scheme. In a previous paper, we proved that their new local models are topologically flat when  $n$ is odd. In the present paper, we prove topological flatness when
$n$ is odd. In the present paper, we prove topological flatness when  $n$ is even. Along the way, we characterize the
$n$ is even. Along the way, we characterize the 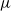 $\mu $ -admissible set for certain cocharacters
$\mu $ -admissible set for certain cocharacters 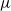 $\mu $ in types
$\mu $ in types 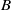 $B$ and
$B$ and 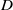 $D$ , and we show that for these cocharacters admissibility can be characterized in a vertexwise way, confirming a conjecture of Pappas and Rapoport.
$D$ , and we show that for these cocharacters admissibility can be characterized in a vertexwise way, confirming a conjecture of Pappas and Rapoport.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 13 , Issue 2 , April 2014 , pp. 303 - 393
- Copyright
- ©Cambridge University Press 2013
References
- 7
- Cited by

