Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Koroteev, Peter
Pushkar, Petr P.
Smirnov, Andrey V.
and
Zeitlin, Anton M.
2021.
Quantum K-theory of quiver varieties and many-body systems.
Selecta Mathematica,
Vol. 27,
Issue. 5,
Koroteev, Peter
and
Zeitlin, Anton M.
2023.
3D Mirror Symmetry for Instanton Moduli Spaces.
Communications in Mathematical Physics,
Vol. 403,
Issue. 2,
p.
1005.
Koroteev, Peter
and
Zeitlin, Anton M
2024.
The Zoo of Opers and Dualities.
International Mathematics Research Notices,
Vol. 2024,
Issue. 8,
p.
6850.
Matsuo, Yutaka
Nawata, Satoshi
Noshita, Go
and
Zhu, Rui-Dong
2024.
Quantum toroidal algebras and solvable structures in gauge/string theory.
Physics Reports,
Vol. 1055,
Issue. ,
p.
1.
Brinson, Ty J.
Sage, Daniel S.
and
Zeitlin, Anton M.
2024.
Opers on the projective line, Wronskian relations, and the Bethe Ansatz.
Journal of Geometry and Physics,
Vol. 202,
Issue. ,
p.
105222.
Koroteev, Peter
2024.
Quantum K-theory and integrability.
International Journal of Modern Physics A,
Vol. 39,
Issue. 33,
Zeitlin, Anton
2024.
Algebraic and Topological Aspects of Representation Theory.
Vol. 791,
Issue. ,
p.
91.
Zeitlin, Anton
2025.
From Representation Theory to Mathematical Physics and Back.
Vol. 817,
Issue. ,
p.
347.
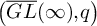 $\left (\overline {GL}(\infty ),q\right )$
-opers with regular singularities and then, by imposing various analytic conditions on singularities, arrive at the desired Bethe equations for toroidal q-opers.
$\left (\overline {GL}(\infty ),q\right )$
-opers with regular singularities and then, by imposing various analytic conditions on singularities, arrive at the desired Bethe equations for toroidal q-opers.