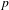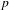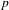Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Betina, Adel
2018.
Les variétés de Hecke–Hilbert aux points classiques de poids parallèle 1.
Journal de théorie des nombres de Bordeaux,
Vol. 30,
Issue. 2,
p.
575.
Deo, Shaunak V.
Dimitrov, Mladen
and
Wiese, Gabor
2024.
Unramifiedness of weight 1 Hilbert Hecke algebras.
Algebra & Number Theory,
Vol. 18,
Issue. 8,
p.
1465.
Diamond, Fred
2024.
Compactifications of Iwahori-level Hilbert modular varieties.
Journal of Number Theory,
Vol. 263,
Issue. ,
p.
255.
Diamond, Fred
2025.
Kodaira–Spencer isomorphisms and degeneracy maps on Iwahori-level Hilbert modular varieties: the saving trace.
Forum of Mathematics, Sigma,
Vol. 13,
Issue. ,