Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T17:27:33.629Z Has data issue: false hasContentIssue false
  • English
  • Français

WITTEN DEFORMATION FOR NONCOMPACT MANIFOLDS WITH BOUNDED GEOMETRY

Published online by Cambridge University Press:  07 June 2021

Xianzhe Dai Open the ORCID record for Xianzhe Dai [Opens in a new window]  and
Junrong Yan
Xianzhe Dai
Affiliation:
Department of Mathematics, UCSB, Santa Barbara, CA, USA (dai@math.ucsb.edu, j_yan@math.ucsb.edu)
Junrong Yan
Affiliation:
Department of Mathematics, UCSB, Santa Barbara, CA, USA (dai@math.ucsb.edu, j_yan@math.ucsb.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Motivated by the Landau–Ginzburg model, we study the Witten deformation on a noncompact manifold with bounded geometry, together with some tameness condition on the growth of the Morse function f near infinity. We prove that the cohomology of the Witten deformation 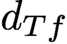$d_{Tf}$ acting on the complex of smooth 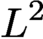$L^2$ forms is isomorphic to the cohomology of the Thom–Smale complex of f as well as the relative cohomology of a certain pair 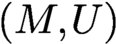$(M, U)$ for sufficiently large T. We establish an Agmon estimate for eigenforms of the Witten Laplacian which plays an essential role in identifying these cohomologies via Witten’s instanton complex, defined in terms of eigenspaces of the Witten Laplacian for small eigenvalues. As an application, we obtain the strong Morse inequalities in this setting.

Keywords

Witten deformationThom–Smale complexAgmon estimate
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 2 , March 2023 , pp. 643 - 680
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution and reproduction, provided the original article is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Agmon, S., Lectures on Exponential Decay of Solutions of Second-Order Elliptic Equations: Bounds on Eigenfunctions of N-Body Schrödinger Operations (Princeton University Press, Princeton, NJ, 2014).CrossRefGoogle Scholar
Bismut, J.-M. and Zhang, W., An extension of a theorem by Cheeger and Müller, Astérisque 205 (1992).Google Scholar
Cheeger, J., Gromov, M. and Taylor, M., Finite propogation speed, kernel estimate for functions of the Laplace operator, and the geometry of complete Riemannian manifolds, J. Diff. Geom. 17 (1982), 15–53.Google Scholar
Chernoff, P. R., Essential self-adjointness of powers of generators of hyperbolic equations, J. Funct. Anal. 12(1) (1973), 401–414.CrossRefGoogle Scholar
Demailly, J. P., Champs magnétiques et inégalités de Morse pour la ${d}^{{\prime\prime} }$ -cohomologie, C. R. Acad. Sci., and Ann. Inst. Fourier 301(35) (1985), 119–122, 185–229.Google Scholar
Dimca, A. and Saito, M., On the cohomology of a general fiber of a polynomial map, Compos. Math. 85 (1993), 299–309.Google Scholar
Fan, H., ‘Schr $\ddot{\mathrm{o}}$ dinger equations, deformation theory and $t{t}^{\ast }$ -geometry’, Preprint, 2011, https://arXiv.org/abs/1107.1290 . Google Scholar
Fan, H. and Fang, H., ‘Torsion type invariants of singularities’, Preprint, 2016, https://arXiv.org/abs/1603.0653.Google Scholar
Fan, H., Jarvis, T. and Ruan, Y., The Witten equation, mirror symmetry and quantum singularity theory, Ann. Math. 178 (2013), 1–106.10.4007/annals.2013.178.1.1CrossRefGoogle Scholar
Farber, M. and Shustin, E., Witten deformation and polynomial differential forms, Geom. Dedicata 80 (2000), 125–155.CrossRefGoogle Scholar
Gromov, M. and Lawson, H. B., Positive scalar curvature and the Dirac operator on complete Riemannian manifolds, Publ. Math. Inst. Hautes Études Sci. 58(1) (1983), 83–196.CrossRefGoogle Scholar
Han, Q. and Lin, F., Elliptic Partial Differential Equations , Vol. 1 (American Mathematical Society, Providence, Rhode Island, 2011).Google Scholar
Helffer, B. and Sjöstrand, J., Puits multiples en mecanique semi-classique iv etude du complexe de Witten, Comm. Partial Differential Equations 10(3) (1985), 245–340.10.1080/03605308508820379CrossRefGoogle Scholar
Hori, K., Katz, S., Klemm, A., Pandharipande, R., Thomas, R., Vafa, C., Vakil, R. and Zaslow, E., Mirror Symmetry , Vol. 1 (American Mathematical Society, Providence, Rhode Island, 2003).Google Scholar
Laudenbach, F., On the Thom-Smale complex, Astérisque 205 (1992), 219–233.Google Scholar
Laudenbach, F., A Morse complex on manifolds with boundary, Geom. Dedicata 153(1) (2011), 47–57.CrossRefGoogle Scholar
Li, S. and Wen, H., ‘On the ${L}^2$ -Hodge theory of Landau-Ginzburg models’, Preprint, 2019, https://arXiv.org/abs/1903.02713.Google Scholar
Lu, W., A Thom-Smale-Witten theorem on manifolds with boundary, Math. Res. Lett. 24(1) (2017), 119–151.CrossRefGoogle Scholar
Milnor, J., Lectures on the $h$ -Cobordism Theorem (Princeton University Press, Princeton, NJ, 2015).Google Scholar
Reed, M. and Simon, B., Methods of Modern Mathematical Physics I: Functional Analysis (Academic Press, New York, NY, 1981).Google Scholar
Witten, E., Supersymmetry and Morse theory, J. Differential Geom. 17(4) (1982), 661–692.CrossRefGoogle Scholar
Witten, E., Phases of $N=2$ theories in two dimensions, Nuclear Phys. B 403 (1993), 159–222.CrossRefGoogle Scholar
Zhang, W., Lectures on Chern-Weil Theory and Witten Deformations (World Scientific, Singapore, 2001).CrossRefGoogle Scholar