Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-14T22:48:06.290Z Has data issue: false hasContentIssue false
  • English
  • Français

A geometric analysis of growth in gastropod shells, with particular reference to turbinate forms

Published online by Cambridge University Press:  06 October 2009

S. U. K. Ekaratne  and
D. J. Crisp
S. U. K. Ekaratne
Affiliation:
N.E.R.C. Unit of Marine Invertebrate Biology, Marine Science Laboratories, Menai Bridge, Gwynedd, LL59 5EH
D. J. Crisp
Affiliation:
N.E.R.C. Unit of Marine Invertebrate Biology, Marine Science Laboratories, Menai Bridge, Gwynedd, LL59 5EH
Get access Rights & Permissions [Opens in a new window]

Abstract

Nucella lapillus and Littorina littorea afford examples of turbinately coiled shells with no space between the columella and the inner face of the whorls. Three constants are sufficient to determine the form of such shells: λ, the ratio between diameters of successive whorls; β, the semi-apical angle and ρ, the ratio of aperture length and breadth in the apertural plane passing through the axis. The variation of these three constants with size was examined and shown to be relatively small and insignificant in Nucella, but in Littorina it was significant.

For Nucella and Littorina these shell characteristics were used to relate for the nth whorl, the length along the shell spiral (ln) to the shell height (Hn), the latter being the measure usually employed in growth studies. This relation was derived mathematically and confirmed empirically as

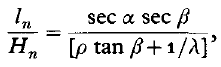
where α is the angle of the logarithmic spiral given by α = tan−1 2π sin β/loge λ. The increased resolution of the micro-growth band increments, which are measured along the shell spiral was directly related to the ln:Hn ratios.

Since the formula for the ln/Hn ratio (= shell conversion factor) includes λ, β and ρ, the three constants necessary to determine shell form in turbinately coiled shells of the type described, the shell conversion factor may be a better index of shell shape than indices based on a single constant. In species where the shell grows isometrically this ratio will remain constant, whereas changes in shell shape with size will influence this ratio. Such changes in shell shape during growth can be quantified in terms of the shell constants and when included in calculating the shell conversion factor, will show the relative magnitude of shell shape changes brought about by growth. The shell conversion factor may also be used to study the effects of ecological variations on the geometry of the shell.

The conical shell of the limpet, Patella vulgata, is geometrically a much simpler system in which direct shell measurements were used to relate length along the direction of maximum growth to the antero-posterior diameter of aperture.

Type
Research Article
Information
Journal of the Marine Biological Association of the United Kingdom , Volume 63 , Issue 4 , November 1983 , pp. 777 - 797
Copyright
Copyright © Marine Biological Association of the United Kingdom 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Cain, A. J., 1977. Variation in the spire index of some coiled gastropod shells, and its evolutionary significance. Philosophical Transactions of the Royal Society (B), 277, 377–428.Google ScholarPubMed
Cain, A. J., 1978 a. The deployment of operculate land snails in relation to shape and size of shell. Malacologia, 17, 207–221.Google Scholar
Cain, A. J., 1978 b. Variation of terrestrial gastropods in the Philippines in relation to shell shape and size. Journal of Conchology, 29, 239–245.Google Scholar
Cain, A. J., 1980. Whorl number, shape, and size of shell in some pulmonate faunas. Journal of Conchology, 30, 209–221.Google Scholar
Crothers, J. H., 1973. On variation in Nucella lapillus (L.): shell shape in populations from Pembrokeshire, South Wales. Proceedings of the Malacological Society of London, 40, 319–327.Google Scholar
Crothers, J. H., 1977 a. Some observations on the growth of the common dog-whelk, Nucella lapillus (Prosobranchia: Muricacea) in the laboratory. Journal of Conchology, 29, 157–162.Google Scholar
Crothers, J. H., 1977 b. On variation in Nucella lapillus (L.): shell shape in populations towards the southern limit of its European range. Journal of Molluscan Studies, 43, 181–188.Google Scholar
Crothers, J. H., 1979. Variation in the shell of the dog-whelk, Nucella lapillus (L.) from Sullom Voe and other parts of the Shetland Islands. Marine Environmental Research, 2, 311–326.CrossRefGoogle Scholar
Crothers, J. H., 1981. Shell-shape variation in Faroese dogwhelks (Nucella lapillus (L.)). Biological Journal of the Linnean Society of London, 15, 327–337.CrossRefGoogle Scholar
Crothers, J. H. & Cowell, E. B., 1979. On variation in Nucella lapillus (L.) shell shape in populations from Fensfjorden, Norway: an applied example. Journal of Molluscan Studies, 45, 108–114.Google Scholar
Ebling, F. J., Kitching, J. A., Muntz, L. & Taylor, C. M., 1964. The ecology of Lough Ine. VIII. Experimental observations of the destruction of Mytilus edulis and Nucella lapillus by crabs. Journal of Animal Ecology, 33, 73–82.CrossRefGoogle Scholar
Ekaratne, S. U. K. & Crisp, D. J., 1982. Tidal micro-growth bands in intertidal gastropod shells, with an evaluation of band-dating techniques. Proceedings of the Royal Society (B), 214, 305–323.Google Scholar
Ekaratne, S. U. K. & Crisp, D. J., 1983. Seasonal growth studies of intertidal gastropods from shell micro-growth band measurements, including a comparison with alternative methods. Journal of the Marine Biological Association of the United Kingdom, 63(4). (In the Press.)Google Scholar
Fretter, V. & Graham, A., 1962. British Prosobranch Molluscs: Their Functional Anatomy and Ecology. 755pp. London: Ray Society.Google Scholar
Gibson, J. S., 1970. The function of the operculum of Thais lapillus (L.) in resisting desiccation and predation. Journal of Animal Ecology, 39, 159–168.CrossRefGoogle Scholar
Gruffydd, LL. D. & Baker, W. F., 1969. An integrated multiple unit controlled temperature system for sea water aquaria. Laboratory Practice, 18, 300–304.Google Scholar
Hughes, R. N. & Elner, R. W., 1979. Tactics of a predator, Carcinus maenas, and morphological responses of the prey, Nucella lapillus. Journal of Animal Ecology, 48, 65–78.CrossRefGoogle Scholar
Kitching, J. A., Muntz, L. & Ebling, F. J., 1966. The ecology of Lough Ine. XV. The ecological significance of shell and body forms in Nucella. Journal of Animal Ecology, 35, 113–126.CrossRefGoogle Scholar
Linsley, R. M., 1978 a. Locomotion rates and shell form in the gastropoda. Malacologia, 17, 193–206.Google Scholar
Linsley, R.M., 1978 b. Shell form and the evolution of gastropods. American Scientist, 66, 432–441.Google Scholar
Moore, H. B., 1936. The biology of Purpura lapillus. I. Shell variation in relation to environment. Journal of the Marine Biological Association of the United Kingdom, 21, 61–89.CrossRefGoogle Scholar
Moore, H. B., 1937. The biology of Littorina littorea. Part I. Growth of the shell and tissues, spawning, length of life and mortality. Journal of the Marine Biological Association of the United Kingdom, 21, 721–742.CrossRefGoogle Scholar
Moseley, H., 1838. On the geometrical form of turbinated and discoid shells. Philosophical Transactions of the Royal Society, 1838 (1), 351–370.Google Scholar
Moseley, H., 1842. On conchyliometry. London, Edinburgh and Dublin Philosophical Magazine and Journal of Science, 21, 300–305.Google Scholar
Newkirk, G. F. & Doyle, R. W., 1975. Genetic analysis of shell-shape variation in Littorina saxatilis on an environmental cline. Marine Biology, 30, 227–237.CrossRefGoogle Scholar
Palmer, A. R., 1980. Locomotion rates and shell form in the Gastropoda: a re-evaluation. Malacologia, 19, 289–296.Google Scholar
Raup, D. M., 1961. The geometry of coiling in gastropods. Proceedings of the National Academy of Sciences of the United States of America, 47, 602–609.CrossRefGoogle ScholarPubMed
Raup, D. M., 1962. Computer as an aid in describing form in gastropod shells. Science, New York, 138, 150–152.CrossRefGoogle ScholarPubMed
Raup, D. M., 1966. Geometric analysis of shell coiling: general problems. Journal of Paleontology, 40, 1178–1190.Google Scholar
Raup, D. M. & Michelson, A., 1965. Theoretical morphology of the coiled shell. Science, New York, 147, 1294–1295.CrossRefGoogle ScholarPubMed
Reimchen, T. E., 1982. Shell size divergence in Littorina mariae and L. obtusata and predation by crabs. Canadian Journal of Zoology, 60, 687–695.CrossRefGoogle Scholar
Smith, J. E., 1981. The natural history and taxonomy of shell variation in the periwinkles Littorina saxatilis and Littorina rudis. Journal of the Marine Biological Association of the United Kingdom, 61, 215–241.CrossRefGoogle Scholar
Thompson, D. W., 1942. On Growth and Form, vol. 11, 2nd edition. 748–849 pp. Cambridge University Press.Google Scholar
Vermeij, G. J., 1970. Adaptive versatility and skeletal construction. American Naturalist, 104, 253–260.CrossRefGoogle Scholar
Vermeij, G. J., 1971. Gastropod evolution and morphological diversity in relation to shell geometry. Journal of Zoology, 163, 15–23.CrossRefGoogle Scholar
Vermeij, G. J., 1975. Evolution and distribution of left-handed and planispiral coiling in snails. Nature, London, 254, 419–420.CrossRefGoogle Scholar